Základy statistiky v genetice kvantitativních znaků

Normální (Gaussovo) rozdělení pravděpodobnosti

Je rozdělení spojité náhodné proměnné, má funkci hustoty pravděpodobnosti

a distribuční funkci

 

Normální rozdělení o střední hodnotě a varianci zapisujeme N(, ). (Normálně distribuovaná proměnná s průměrem a variancí )
Přibližný rozptyl měření kolem střední hodnoty E(X):

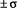• je 68,3 % všech případů
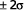• je 95,5 % všech případů
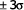• je 99,7 % všech případů

Většina hodnot tedy leží v mezích kolem střední hodnoty, je to tzv. pravidlo tří sigma.

Náhodná veličina

Náhodná veličina (náhodná proměnná) je taková veličina, která jako výsledek nekonečně mnoha pokusů může nabýt nějakou hodnotu, přičemž předem nevíme jakou konkrétně. Náhodnou proměnnou charakterizujeme pomocí pravděpodobnosti, se kterou může nabývat dané hodnoty, tedy pomocí rozdělení (distribuce) pravděpodobností.
Náhodné veličiny rozdělujeme na:

• diskrétní, které nabývají jen konečně nebo spočetně mnoha různých hodnot;
• spojité, jejichž hodnoty spojitě vyplňují určitý interval (konečný nebo nekonečný).

Náhodné veličiny budeme označovat velkými písmeny, např. X, a jejich možné hodnoty odpovídajícími malými písmeny, např. x₁, x₂.

Diskrétní náhodné veličiny můžeme popsat:

1. rozdělením pravděpodobností
2. a distribuční funkcí.

Rozdělením pravděpodobností nazýváme každý předpis, který určuje vztah mezi možnými hodnotami náhodné veličiny x_i a jim příslušejícími pravděpodobnostmi pi = P(X = x_i).
Rozdělení pravděpodobností bývá zadáno tabulkou:

xi	x1	x2	...	xn
pi	p1	p2	...	pn

Pravděpodobnosti p_i vyhovují vztahu

kde počet možných hodnot (n) může být konečný nebo nekonečný.

Distribuční funkce (integrální zákon rozdělení) náhodné veličiny X je funkce F(x), která se rovná pravděpodobnosti P(X < x) toho, že náhodná veličina X nabude hodnoty menší než zvolené číslo x. Pro diskrétní náhodnou veličinu .

Spojité náhodné veličiny můžeme popsat:

1. distribuční funkcí F(x)
2. a hustotou pravděpodobnosti f(x).

Distribuční funkce F(x) =P(X < x) má tyto základní vlastnosti, kde x je libovolné reálné číslo:

• P(a X < b) = F(b) - F(a)
• F(x₁) F(x₂) pro x₁ < x₂
• 
• 

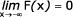
Hustota pravděpodobnosti f(x) má tyto základní vlastnosti:

• je nezáporná
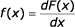• , je derivací distribuční funkce
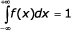• , hodnota X leží v intervalu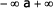
• 

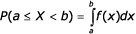
Vlastnosti distribuce - parametry univariátní distribuce

Kvantitativní vlastnosti studované biology jsou trojího typu. Vlastnosti, které jsou distribuované do skupin diskrétních tříd (např. počet selat ve vrhu…), jsou nazývány meristickými vlastnostmi. Vlastnosti měřené na kontinuální stupnici jsou známé jako metrické vlastnosti (např. délka těla, hmotnost...). Vlastnosti, jako jsou přežitelnost k určitému věku, s funkcí buď anebo (ano – ne) jsou binární. Z důvodů technického omezení musí být vlastnost s kontinuální distribucí uměle rozdělena do diskrétních kategorií – intervalů. Těžko budeme při běžném měření metrem rozlišovat mezi jedinci s mírou 34,2 a 34,8 mm. Obě měření umístíme do kategorie 34 – 35 mm.

Univariátní distribuce popisuje frekvenci fenotypů pro jednu vlastnost, bivariátní pro dvě vlastnosti a pro více jak dvě vlastnosti se nazývá multivariátní distribuce.

Jedním z cílů statistiky je popsat data zcela jednoduchými matematickými funkcemi, nazvané pravděpodobnosti distribuce. Jestliže proměnná x má jen diskrétní hodnoty, pak distribuce z je zcela popsána pravděpodobností P(x = x_i) pro každý možný výsledek. Součet všech možných výsledků , protože celkové pravděpodobností všech možných dějů je rovna 1.

 

U kontinuální vlastnosti nedává P(x = x_i) smysl, protože pravděpodobnost, že nabude x nějakou specifickou hodnotu je nekonečně malá (infinitesimální). Je pak vhodnější myslet, že s pravděpodobností leží x ve specifikovaném rozpětí hodnot, x₁ a x₂. Počet je pak popsán funkcí hustoty pravděpodobnosti p(x): .

Jestliže x₁ a x₂ jsou horní a dolní hranicí x, pak p(x) = 0 mimo toto rozpětí a nad celým rozsahem. Pravděpodobnost není nikdy negativní a celková pravděpodobnost všech možných výsledků je rovna jedné.

Odhad a parametr

Je třeba rozlišovat mezi pravým parametrem distribuce a odhadem tohoto parametru. Hodnoty pravého parametru mohou být získány, jestliže každý člen populace je měřen s absolutní přesností. Téměř vždy se však řeší aproximace, přibližné odhady. Přesnost pak závisí na experimentálních podmínkách, měřících přístrojích a velikosti populace. Označení: parametry se většinou označují řeckými symboly a odhady latinkou.

Většina použitelných funkcí pravděpodobnosti hustoty je definována dvěma parametry, popisující centrální polohu a rozptyl. Hlavním parametrem centrální polohy je aritmetický průměr, , označovaný jako první moment zdroje. Jestliže p(x) je funkce pravděpodobnosti hustoty fenotypu x, pak vážení všech hodnot x jejich hustotou vede k:

kde E(x) je očekávaná hodnota x. Pro diskrétní vlastnosti, .

Výběrový odhad průměru vlastnosti x se obecné označuje , a odhaduje se jako průměr n měření:

Míra rozptylu frekvence distribuce je druhý moment nad průměrem – variance (rozptyl). Variance je očekávaný čtverec odchylek pozorování od jeho průměru,

Protože m = E(x), může být tento počet zjednodušen rozvinutím (x - )² a lze získat:

Komplikovanější je odhad parametru z náhodného výběru z populace. Pravý parametr a odhad E(x²) nemůžou být známy s přesností, dokud není vybrána celá populace. Se zvýšením počtu pozorování se snižuje vychýlenost odhadu. Nevychýlený odhad variance z malého výběru populace získáme jednoduše:

Výpočtový tvar:

=>

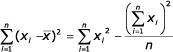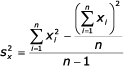
Směrodatná odchylka je míra variability vyjádřená v jednotkách vlastnosti. Jedná se o druhou odmocninu variance. Parametrová hodnota je označována jako sx a odhad jako sx. Ve statistických programech se označuje zkratkou SD (standard deviation).

Podíl směrodatné odchylky a průměru je varianční koeficient:

• Parametrový index 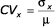a odhad .

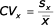Průměr výběrového souboru je také náhodná veličina. Provede-li se výběr z téhož základního souboru vícekrát, jejich průměry se budou lišit. Tato variance je vyjádřena střední chybou průměru (přesnost odhadu průměru). Ve statistických programech se označuje zkratkou SE (standard error).

• Parametrový index 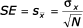a odhad .

 

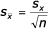Aktualizováno: 03.02.2015