Kovariance, regrese a korelace
Jsou dále nutné další statistiky, kromě rozptylu či průměru univariátní distribuce, které jsou nutné k popisu společné distribuci dvou nebo více proměnných. Kovariance poskytuje přirozenou míru asociace mezi dvěma proměnnými a objevuje se tak v mnoha analýzách v kvantitativní genetice včetně podobnosti mezi příbuznými jedinci, korelace mezi vlastnostmi a měření selekce.
Společná distribuce náhodných proměnných
Funkce společné pravděpodobnosti hustoty p(x, y) specifikuje pravděpodobnost společného výskytu páru náhodných proměnných (x, y):
![]()
Častá otázka bývá, jaká je distribuce vlastnosti y daná, když vlastnost x se rovná určité specifické hodnotě? Chceme např. vědět pravděpodobnost, že rodiče, jejichž užitkovost má hodnotu 7500 kg mléka, budou mít potomky s užitkovostí 7650 kg mléka. Pro odpověď se používá podmíněná hustota y daná y, kde:
![]()
Funkce společné hustoty pravděpodobnosti, p(x, y), a funkce podmíněné hustoty p(y|x) jsou spojeny:
p(x, y) = p(y|x) p(x)
kde ![]() je marginální (univariátní) hustota x.
je marginální (univariátní) hustota x.
Dvě proměnné jsou nezávislé, jestliže p(x, y) rozčleněna do součinu pouze funkcí x a y: p(x,y) = p(x).p(y). Pak také p(y|x) = p(y).
Jsou li x a y nezávislé, pak znalost hodnoty x nedává žádnou informaci o hodnotě y.
Očekávané společné distribuce proměnných
Očekávané hodnoty bivariátní funkce, f(x,y) jsou určeny společnou pravděpodobností hustoty:
![]()
Podmíněné očekávání (očekávaná hodnota jedné proměnné, daná informací druhé):
![]()
Vlastnosti x a y jsou nezávislé, když E(y|x) = E(y). Dále E(y|x) je funkcí specifické hodnoty x.
Kovariance
Uvažujme sadu párovaných proměnných (x, y). Pro každý pár se odečítá hodnota x od populačního průměru ![]() x a y od populačního průměru
x a y od populačního průměru ![]() y . U každého párového pozorování jsou navzájem násobeny tyto rozdíly: (x -
y . U každého párového pozorování jsou navzájem násobeny tyto rozdíly: (x - ![]() x). (y -
x). (y - ![]() y ).
y ).
Kovariance mezi vlastnostmi x a y je definována jako průměr těchto kvantit přes všechny páry vlastností x a y měřené v populaci: ![]() .
.
Často se kovariance označuje ![]() x,y nebo cov(x,y). Protože E(x) =
x,y nebo cov(x,y). Protože E(x) = ![]() x a E(y) =
x a E(y) = ![]() y , lze tento součin rozšířit a zjednodušit:
y , lze tento součin rozšířit a zjednodušit:

Slovy, kovariance je průměr součinů párových vlastností x a y mínus součin jejich průměrů. Kovariance vyjadřuje míru vazby mezi náhodnými proměnnými.
![]()
kde ![]()
Výběrová kovariance: ![]()
a výpočtový vzorec: ![]()
Regrese
Příčinná závislost mezi dvěma proměnnými, x a y, jejich vztah, může být lineární nebo nelineární. Avšak asociace jsou vždy převáděny na lineární model, který slouží jako první přibližný odhad. Nejjednodušší regresní lineární model je:
![]()
kde ![]() je intercept,
je intercept, ![]() je směrnice přímky (označovaný jako regresní koeficient) a e je reziduální chyba. Nechť:
je směrnice přímky (označovaný jako regresní koeficient) a e je reziduální chyba. Nechť:
![]()
je předpověděná hodnota y modelem, pak reziduální chyba je odchylka mezi pozorovanou a očekávanou hodnotou y, ![]() . Je-li použita hodnota x k předpovědi y, je x označována jako nezávisle proměnná a y je závisle proměnná. Cíle lineární regresní analýzy je odhadnout parametry modelu,
. Je-li použita hodnota x k předpovědi y, je x označována jako nezávisle proměnná a y je závisle proměnná. Cíle lineární regresní analýzy je odhadnout parametry modelu, ![]() a
a ![]() , tak že dávají nejlepší odhad společné distribuce x a y.
, tak že dávají nejlepší odhad společné distribuce x a y.
- Řešení pro intercept:
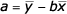
- Řešení pro směrnici lineární regrese:
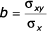
- nutné zná hodnoty průměrů, variancí a kovariance
Korelace
Nejčastěji používanou mírou v bivariátních analýzách je korelační koeficient: ![]()
Vztah mezi regresním a korelačním koeficientem je: ![]()
Aktualizováno: 03.02.2015
