Analýza variance - ANOVA

1. Příklad jednofaktorové analýzy variance hodnocení fenotypové proměnlivosti snášky u slepic jednoho chovu. Na základě jednofaktorové analýzy variance chceme zjistit, zda existují průkazné rozdíly ve snášce u potomstva po čtyřech kohoutech, chceme znát, zda genetický vliv otec byl průkazný nebo neprůkazný. Ve sledování jsou čtyři skupiny slepic a v každé je potomstvo po jednom ze čtyř kohoutů, jedná se tedy o skupiny polosourozenců. Tabulka zjištěných hodnot:

	i = 1 (k1)		i = 2 (k2)		i = 3 (k3)		i = 4 (k4)
1	172	29584	137	18769	209	43681	172	29584
2	253	64009	197	38809	187	34969	166	27556
3	239	57121	200	40000	183	33489	121	14641
4	203	41209	198	39204	215	46225	115	13225
5	247	61009	131	17161	215	46225	134	17956
6	256	65536	145	21025	134	17956	134	17956
7					185	34225	127	16129
8					218	47524	115	13225
9					155	24025	138	19044
10					214	45796	116	13456
11					184	33856	124	15376
12					176	30976	197	38809
13							118	13924
14							129	16641
15							113	12769
16							138	19044
17							133	17689
18							116	13456
19							112	12544
20							114	12996
21							110	12100
22							124	15376
23							118	13924
24							138	19044
	1370	318468	1008	174968	2275	438947	3122	416464

 

Model jednofaktorové analýzy variance: y_ij = + a_i + e_ij

• y_ij – užitkovost j-tého potomka po i-tém otci
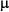• – obecný průměr populace
• a_i – vliv i-tého otce
• e_ij – ostatní nahodilé vlivy

Předpočítané hodnoty:

kohouti						ni
k1	1370	228,33	1876900	312816,67	318468	6
k2	1008	168,00	1016064	169344,00	174968	6
k3	2275	189,58	5175625	431302,08	438947	12
k4	3122	130,08	9746884	406120,17	416464	24
Y..	= 7775			1319582,92	1348847	n = 48
Y2..	= 60450625					i = 4

 

Výpočet součtu čtverců odchylek od průměru:

• pro celý pokus: S_c =
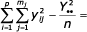
• pro skupiny: S_a =
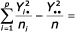
• reziduální: S_e =

 

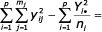
Tabulka analýzy variance:

Zdroj proměnlivosti	Součet čtverců odchylek (S)	Stupeň volnosti (f)	Průměrný čtverec (MS)	Složení MS
mezi skupinami	Sa	fa = i -1	MSa =
uvnitř skupin	Se	fe = n – i	MSe =
celková	Sc	fc = n – 1

 

Dopočítaná tabulka analýzy variance z příkladu:

Proměnlivost	S	f	MS	F
Mezi skupinami	60194,90	3	20064,97	30,17
Uvnitř skupin	29264,08	44	665,09
Celková	89458,98	47

 

Hodnota F testu:

Vyhodnocení F testu: F_vyp. > F_tab. F_{(3; 44; 0,05)} = 2,28 F_{(3; 44; 0,01)} = 4,26

Mezi skupinami polosourozenců existují v rámci sledované proměnlivosti snášky vajec u slepic vysoce průkazné rozdíly, které byly podmíněny příbuzenským vztahem ze strany otce, tedy geneticky.

Následuje výsledek této analýzy variance, která byla provedena v programu SAS.

The ANOVA Procedure

Dependent Variable: snaska

Source DF Sum of Squares Mean Square F Value Pr > F

Model 3 60194.89583 20064.96528 30.17 <.0001

Error 44 29264.08333 665.09280

Corrected Total 47 89458.97917

R-Square Coeff Var Root MSE snaska Mean

0.672877 15.92143 25.78939 161.9792

Source DF Anova SS Mean Square F Value Pr > F

kohouti 3 60194.89583 20064.96528 30.17 <.0001

---

2. Příklad hierarchické dvoufaktorové analýzy proměnlivosti. Na stanici pro zkoušky výkrmnosti a jatečné hodnoty prasat, za jednotného krmení a ustájení bylo vybráno potomstvo dvou kanců (k1 a k2), které pocházelo z vrhů několika prasnic (p1 až p6). Chceme zjistit, zda kanci a prasnice měli genetický vliv na přírůstky kontrolovaných potomků hodnocených počtem dnů ve výkrmu z hmotnosti 40 kg do hmotnosti 110 kg.

Kanci	k1			k2
Prasnice	p1	p2	p3	p4	p5	p6
Potomci	93	107	109	89	87	81
yijk	89	99	107	102	91	83
	97		94	104	82	85
	105		106	97		91
nij	4	2	4	4	3	4
ni	10			11

 

Model dvoufaktorové hierarchické analýzy variance: y_ij = + a_i + b_ij + e_ij

• y_ijk – užitkovost k-tého potomka po j-té prasnici a i-tém otci
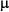• – obecný průměr populace
• a_i – vliv i-tého otce
• b_ij – vliv j-té matky pod i-tým otcem
• e_ijk – ostatní nahodilé vlivy

Předpočítané hodnoty: k = 2; p = 6

		Yij.		Yi.				nij	ni
	p1	384	36864	1006	101203,6			4
k1	p2	206	21218					2
	p3	416	43264					4	10
	p4	392	38416	992	89460,36			4
k2	p5	260	22533,33					3
	p6	340	28900					4	11
		1998	191195,33	1998	190663,96	190095,43	191736	21
		Y..		Y..				n

 

Výpočet součtu čtverců odchylek od průměru:

• pro skupiny mezi kanci S_a =
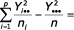
• pro skupiny mezi prasnicemi S_b =
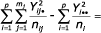
• reziduální (mezi potomky) S_e =
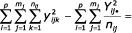
• pro celý pokus S_c =

 

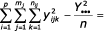
Tabulka analýzy variance:

Zdroj proměnlivosti	Součet čtverců odchylek (S)	Stupeň volnosti (f)	Průměrný čtverec (MS)	Složení MS
- mezi otci	Sa	fa = k -1	MSa =
- mezi matkami uvnitř otců	Sb	fb = p – k	MSb =
- mezi potomky uvnitř skupin podle matek	Se	fe = n – p	MSe =
- celková	Sc	fc = n – 1

 

Dopočítaná tabulka analýzy variance:

Proměnlivost	S	f	MS	F
Mezi otci (a)	568,54	1	568,54	15,77
Mezi matkami uvnitř otců (b)	531,37	4	132,84	3,69
Uvnitř skupin (e)	540,67	15	36,04
Celková (c)	1640,57	20

Hodnota F testu:

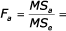• 15,77
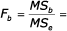• 3,69

Vyhodnocení F testu:

• vliv otců F_vyp. > F_{tab. 0,01} F_{(1; 15; 0,05)} = 4,54 F_{(1; 15; 0,01)} = 8,68
• vliv matek F_vyp. > F_{tab. 0,05} F_{(4; 15; 0,05)} = 3,06 F_{(4; 15; 0,01)} = 4,89
  

 

Genetický vliv otců byl vysoce průkazný a genetický vliv matek byl průkazný na přírůstky kontrolovaných potomků. Vzhledem k velmi malému souboru vlastních sourozenců není možné zjišťoval genetický podíl otců a matek a proto se vyhodnocoval jen jejich vliv.

 

Následuje výsledek této analýzy variance, která byla provedena v programu SAS:

The ANOVA Procedure
Dependent Variable: PRIR
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 5 1099.904762 219.980952 6.10 0.0028
Error 15 540.666667 36.044444
Corrected Total 20 1640.571429
R-Square Coeff Var Root MSE PRIR Mean
0.670440 6.310198 6.003703 95.14286
Source DF Anova SS Mean Square F Value Pr > F
OTEC 1 568.5350649 568.535064915.77 0.0012
OTEC(MATKA) 4 531.3696970 132.8424242 3.69 0.0278

Aktualizováno: 01.03.2011