Markery a výpočty BLUP

Gametický model

BLUP je v současnosti základní metoda pro předpověď plemenných hodnot zvířat na základě fenotypových hodnot zvířat a jejich příbuzných – aditivně genetický vztah mezi příbuznými bez znalosti konkrétního příspěvku rodičů svým potomkům. Infinitesimální animal model předpokládá velký počet nezávislých aditivních lokusů ovlivňujících fenotypy jedinců malým účinkem. Navíc vyžaduje znalost kompletního rodokmenu pro získání nevychýlených odhadů PH. Obdobně může být použit k předpovědi PH i gametický model (2 gamety na 1 zvíře), i když počet rovnic pro řešení je dvakrát větší než v animal modelu.

Gametické modely byly také aplikované na analýzu imprintingu (Gibson et al., 1988). Existuje také možnost jak pomocí gametického modelu odhadovat efekt jednoho lokusu (van Arendonk et al., 1994; Yazdi, Schaeffer, 2002). V určitých případech je užitečné vyjádřit PH v termínech oddělených gametických příspěvků každého ze dvou rodičů (např. když chceme určit parentální PH ). V tomto modelu je aditivně genetická hodnota každého jedince projevena v termínech jeho rodičovských plemenných hodnot. Nechť a_oi a a_mi jsou plemenné hodnoty pro individuálního i-tého otce a i-tou matku, pak i-tá plemenná hodnota potomka je:

součet jejich předpovězené hodnoty (průměrná PH rodičů) a náhodné odchylky (e_ai) vyplývající z mendelistické segregace. Tuto rovnici můžeme přepsat do animal modelu: y_i= +a_i + e_i.

Budeme předpokládat, že fenotypová vlastnost je podmíněna 1 lokusem s mnoha alelama a že všechna zvířata byla genotypována. Matice gametických vztahů (~ příbuznosti) pro jeden lokus kopíruje přenos alel od každého rodiče k jejich potomkům – matice H_i pro i-tý lokus. Tato matice je obecně singulární (nelze ji invertovat). Tvoří se podobně jako matice aditivní příbuznosti. Lze zohlednit i inbríding. S touto maticí je asociována genetická variance .

Gametická matice:

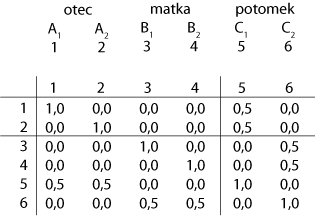
V infinitesimálním modelu jsou všechny lokusy nezávislé v neselektované populaci. Matice H_i může být konstruována pro každý lokus. Součet všech matic H_i by měl být roven matici celkových gametických vztahů (genetická matice příbuznosti, což je variančně kovarianční matice mezi gametami) G(0,5). Genetický efekt pro i-tý lokus je pak a je odhadován jako:

,

kde je celková aditivně genetická variance. Je-li již vypočítán, pak mohou být aplikovány různé matice H_i pro předpověď genetických efektů různých lokusů.

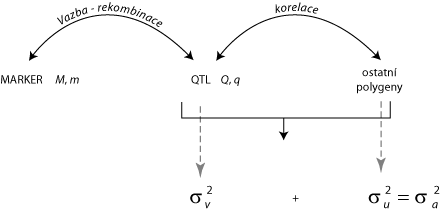
Matice vztahů marker-QTL

Pokud byl lokus major genem nebo QTL, pak není aplikován infinitesimální model. Další procedury budou jen aproximace závisející na poměru  a (0,5). Čím je poměr větší tím je aproximace horší. Lze to aplikovat také na lokusy markerů, kdy vztah marker QTL závisí na síle vazby obou lokusů.

Budeme-li předpokládat, že genotypy zvířete jsou lokusy markeru a ne QTL a rekombinační stupeň mezi nimi je r jednotek, pak gametická matice vztahů (M) pro QTL je konstruována s použitím markerových genotypů a stupně rekombinace (). Známe tedy markerové alely, ale ne počet QTL alel. Protože marker je vázán ke QTL (jsou ve vazbové nerovnováze) a mohou probíhat rekombinace mezi generacemi, jsou očekávány efekty marker-QTL v čase více a více menší, kdy se znovu vytváří vazbová rovnováha.

Tato metoda předpokládá, že G(0,5) je aplikována na všechny lokusy ovlivňujících vlastnost a že cílem je rozdělit ji do efektů způsobených jednotlivými QTL nebo markery.  Předpověď gametických efektů pro každé zvíře se počítá z rovnic smíšeného modelu. Předpokládá se, že matice vztahů H_i pro jeden lokus je právě jedna z nekonečného počtu takových matic, které jsou částí matice G. Použitím principů Henderson (1985) je snadné předpovědět gametický efekt jednoho lokusu z celkových gametických efektů.

 

 

Budeme-li vycházet z modelu navrženého Fernando, Grossman (1989), lze současně odhadovat efekty markerových alel a zbývajících polygenních efektů pomocí rovnice: y = Xb + Zu + Wv + e,

kde u je vektor polygenních efektů, které jsou nezávislé na QTL s jedním efektem na jedince, v je vektor alelických efektů marker-QTL (dva na každé zvíře), b je vektor pevných efektů a X, Z a W jsou incidenční matice, které se vztahují k pozorování - korespondujících efektů (efekty pevné, polygenní a gametické QTL), takže:

, kde

Matice A a Z jsou stejné jako v animal modelu. Vektor u může být nahrazen g, gametickým efektem (dva na jedince) a A může být nahrazen G(0,5). G – genetická matice příbuznosti při dané rekombinaci markeru ke QTL (je nutné zohlednit c.-o. s rekombinacemi).

Není-li znám marker u jedince, provede se úprava matice příbuznosti pro rovnice smíšeného modelu (MME):

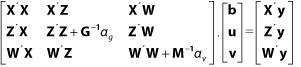
kde a

Tato procedura závisí na rozdílech mezi . Čím větší je , tím lepší bude model.

V modelu předpokládající konečný počet lokusů nemůže být G(0,5) použit pro polygenní efekty v klasickém modelu (Fernando, Grossman, 1989). Místo toho, G() může být odvozen pro každý lokus a sečten za všechny sledované lokusy. Individuální efekt lokusu lze získat z:

Prakticky však je obtížné vypočítat H^-1 v souboru velkého počtu zvířat, což je potenciálním problém pro praktickou aplikaci.

 

Aktualizováno: 09.12.2008