Odhad PH – BLUP AM

V animal modelu (AM) se hodnotí každé zvíře samostatně a současně v závislosti na užitkovosti příbuzných jedinců hodnocené populace. Veškeré příbuzenské vztahy (pokud jsou známé) jsou zahrnuty do aditivně genetické matice příbuznosti. V AM je pro každé zvíře sestavena zvlášť rovnice a to je velký problém, neboť je třeba řešit mnoho rovnic.

BLUP - AM se provádí pomocí distribuční funkce f(T/y)

• T – hledané veličiny (vektor)
  
• y – naměřené užitkovosti (vektor)

Parciální derivací distribuční funkce (první derivace = 0 -> směrnice tečny je nulová – extrém) -> hledáme průběh a extrém funkce -> pomocí soustavy normálních rovnic (maticová soustava) – Mixed Model Equation (MME) – smíšené modely:

(W´R^-1W + H^-1)T = W´R^-1y

• W – matice plánu experimentu, incidenční, designová (odhad PH) – rozepisuje se na matice X a Z !
  
• R – kovarianční matice reziduí (chyb v datech)
  
• H – kovarianční matice mezi hledanými veličinami
  
• T – hledaná veličina

Dále se řeší modelová rovnice: smíšený lineární model y_ijk= b_i+ u_j+ e_ijk (b_i – efekt plemene i - pevný efekt; u_j – efekt otce j na produkci jeho dcer - náhodný efekt)

- (maticový zápis):   y = Xb + Zu + e

Aditivní plemenné hodnoty jsou náhodnými efekty se známou variančně-kovarianční maticí. U vektorů u a e se předpokládá, že mají normální rozdělení a tedy odhadovaná střední hodnota je E(u) = E(e) = 0. Vektor pozorování y má multivariátní normální rozdělení s průměrem Xb (E(y) = Xb) a variancí V (variančně kovarianční matice vektoru pozorování) vypočítanou jako:

V = V(Zu + e) =ZGZ` + R !

kde G je variančně kovarianční matice vektoru náhodných efektů u ~ V(u) a R je variančně kovarianční matice reziduálních chyb ~ V(e).

Nejsou-li otcové příbuzní pak je matice G = I, kde I je jednotková matice a je variance mezi skupinami potomků podle otců a je ¼ aditivní genetické variance (protože každý otec dá ½ svých genů dcerám a po umocnění pro získání variance získáme ¼ aditivní genetické variance).

Jsou-li otcové příbuzní pak G = A, kde A je matice příbuznosti mezi otci s jedničkami na diagonále a mimo diagonální prvky zobrazují podíl genů, které dva jedinci mají od společného předka. Obě matice jsou symetrické (G =G` a A =A`).

BLUP

Nejlepší lineární nevychýlená předpověď (BLUP) vektoru u je:,

kde je odhadce pevných efektů získaných metodou zobecněných nejmenších čtverců (GLS - General Linear Squares).

Rovnice y = Xb + Zu + e  se rozepisuje do soustavy normálních rovnic smíšeného modelu (MME - Mixed Model Equations), z kterých chceme vypočítat vektor T.

 

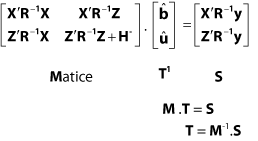
y – vektor naměřených užitkovostí (n)	(n x 1)
X – incidenční matice udávající plán pokusu pevných efektů X	(n x p)
Z – incidenční matice udávající plán pokusu náhodných efektů Z	(n x q)
b – vektor odhadů pevných efektů (odhad úrovní p)	(p x 1)
u – vektor odhadů náhodných efektů; u ~ PH (odhad úrovní q)	(q x 1)
e – vektor nekontrolovatelných náhodných reziduálních efektů (vektor reziduálních odchylek, u kterých se předpokládá, že jsou nezávislé na náhodných genetických efektech	(n x 1)
– kovarianční matice inverzní

Stejně jako v modelu s pevnými efekty se obecně předpokládá, že rezidua jsou nekorelována a mají stejnou, konstantní varianci. Pak R = I, kde je reziduální variance a R^-1 = I/. Takže soustava normálních rovnic může být zjednodušena vynásobením obou stran reziduální variancí (maticí R) a získáme rovnice: 

Pokud předpovídáme plemennou hodnotu pomocí AM (jsou známy příbuzenské vztahy mezi jedinci) nabývají rovnice tvar:

X`X – diagonální matice s řádky a sloupci rovno počtu úrovní pevného efektu (např. počtu plemen), diagonální prvky jsou počty záznamů v korespondující úrovni efektu (konkrétního plemene), mimodiagonální prvky jsou rovny nule
Z`Z – diagonální matice, kde každý diagonální prvek je roven počtu záznamů (počtu dcer) každé úrovně náhodného efektu (otce)
X`Z – matice s počtem řádků rovno počtu úrovní pevných efektů (počet plemen) a počtem sloupců rovno počtu úrovní náhodných efektů (počet otců); každý prvek bude číslo záznamů v odpovídající kombinaci pevného x náhodného efektu (plemeno x otec)
Z`X – matice je transponovaná matice X`Z
X`y – vektor jehož délka bude rovna počtu úrovní pevného efektu (počtu plemen) a každý prvek je součet hodnot v odpovídající úrovni efektu (plemene)
Z`y – vektor jehož délka bude rovna počtu úrovní náhodného efektu (počtu otců) a každý prvek je součet hodnot v odpovídající úrovni efektu (užitkovost všech dcer po každém otci)
A – aditivně genetická matice příbuznosti, jejíž prvky a_ii jsou rovny (1 + Fz) (Fz koeficient inrídingu) a prvky a_ij jsou rovny koeficientům příbuznosti Rij mezi jedinci i a j.

Řešení rovnic smíšeného modelu může být obtížné získat, protože řešení rovnic je prováděno invertováním matic, což je pro běžné výpočty u velkých populací HZ méně vhodné: T = M^-1S. Přesné řešení vyžaduje inverzi matice koeficientů (M), která je zpravidla menší než matice V. Počet řádků a sloupců matice V je rovna celkovému počtu pozorování, zatímco v matici M jsou rovny počtu úrovní efektů zahrnutých do modelu, což je obecně mnohem méně.

Je-li zahrnuto do modelové rovnice více faktorů, může být získáno přibližné řešení iterativními postupy (iteracemi) – řešení jednotlivých rovnic izolovaně, a jejich řešení je využito v dalších rovnicích s cílem stabilizace řešení, kdy se již nemění od jednoho iteračního kola k druhému. Existuje mnoho iteračních metod aplikovatelné na rovnice smíšeného modelu. Nejpoužívanější metodou jsou iterace Gauss-Seidel, protože je relativně rychlá a spolehlivě konverguje a poskytuje řešení rovnic. Animal model vyžaduje několik stovek kol iterací, než se získá přibližná konvergence.

 

Porovnání zobecněného lineárního modelu GLM (general linear model), který obsahuje jen pevné efekty, se smíšeným modelem MM (mixed model):

GLM	MM
yij = + bi + eij	yijk = + bi + uj + eijk
y = Xb + e*	y = Xb + Zu + e
e*~ (0, V)	u ~ (0, G) e ~ (0, R)
y ~ (Xb, V)	y ~ (Xb, V) = (Xb, ZGZ` + R)

• ~ (a, b) znamená, že náhodná proměnná má průměr a a varianci b;
• ve smíšeném modelu je vektor reziduálních efektů rozdělen do dvou komponent  e* =Zu + e

 

Ve smíšeném modelu pozorujeme y, X a Z, zatímco b, u, R a G  jsou obecně neznámé. Takže smíšené modely nám umožňují:

1. odhadovat vektory pevných b a náhodných efektů u
2. odhadovat kovarianční matice G a R (u kterých se předpokládá, že jsou funkcemi několika neznámých komponent variance)

 

Pro pevné efekty platí BLUE (nejlepší lineární nevychýlený odhad): .

Řešení náhodných efektů je BLUP (nejlepší lineární nevychýlená předpověď) , protože náhodné efekty nejsou parametry a jejich řešení se nazývají prediktory „predictors“ a naopak u pevných efektů hovoříme o odhadcích „estimators“.

Odhadujeme pevné efekty a předpovídáme náhodné efekty !!

BLUE a BLUP jsou nejlepší, protože minimalizují výběrovou varianci; lineární v tom smyslu, že jsou lineárními funkcemi pozorovaných fenotypů y; nevychýlené ve smyslu, že E[BLUE(b)] = b a E[BLUP(u)] = u.

 

Pro smíšený model y = Xb + Zu + e platí (Henderson, 1963):

• BLUE pro pevné efekty b:

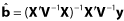
  • kde  V = ZGZ` + R 

  • Jedná se odhadce zobecněných nejmenších čtverců (GLS)

• BLUP pro náhodné efekty u:

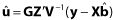
Praktická aplikace obou rovnic vyžaduje známé komponenty variance. Před analýzami BLUP je nutné odhadnout komponenty variance pomocí ANOVA nebo REML.

 

Aktualizováno: 07.10.2008