Genetika populací - organizace genetické variability - Hardy

Hardy-Weinbergův princip

Genotypové frekvence jsou určovány z části typem páření. Musíme předpokládat náhodné páření v modelu nepřekrývajících se populací. Pro vyvozování genotypových frekvencí za náhodného páření je třeba dalších předpokladů:

frekvence alel by se neměly měnit z generace na generaci, protože jinak působí systematické evoluční síly (mutace, migrace, přirozená selekce); tyto evoluční síly nepůsobí nebo mají malou velikost,
populace musí být dostatečně velká, aby frekvence alel nepodléhala změnám při výběrové chybě (variabilita ve frekvenci alel způsobená chybou výběru v malých populacích se nazývá náhodný genetický drift). Tento proces lze ignorovat, pokud má populaci kolem 500 jedinců a více.

Souhrn předpokladů:

organizmus je diploidní,
reprodukce je pohlavní,
generace se nepřekrývají,
sledované geny mají dvě alely,
frekvence alel jsou stejné u samců i u samic,
páření je náhodné,
velikost populace je velmi velká (teoreticky nekonečná) a náhodný genetický drift je zanedbatelný,
migrace je zanedbatelná,
mutace se opomíjí,
přirozená selekce neovlivňuje studované alely.

Tyto předpoklady souhrnně vyjadřují Hardy-Weinbergův model, pojmenovaný podle anglického matematika G.H. Hardyho (1877-1947) a německého fyziologa Wilhelma Weinberga (1862-1937), kteří v roce 1908 nezávisle na sobě publikovali model a vyvodili jeho teoretické předpovědi o genotypových frekvencích.

V Hardy-Weinbergově modelu je popsán matematický vztah mezi frekvencemi alel a frekvencemi genotypů:

AA: p²
Aa: 2pq
aa: q²

kde p², 2pq a q² jsou frekvence genotypů AA, Aa a aa v zygotách v každé generaci, p a q jsou frekvence alel A a a v gametách předcházející generace a p + q = 1. Výše zmíněné frekvence tvoří Hardy-Weinbergův princip nebo-li Hardy-Weinbergovu rovnováhu (HWE).

Uvažujme jeden lokus se dvěma alelami, A a a. Pak

p = f(A); q = f(a)

Ve velké populaci při náhodném páření jsou vztahy mezi frekvencemi alel a genotypů předpověditelné.

Ve velké náhodně se pářící populaci bez selekce, mutace či migrace jsou frekvence alel a genotypů konstantní z generace na generaci a uspořádání frekvencí genotypů v zygotách je dáno uspořádáním frekvencí alel v gametách. U druhů s diploidním počtem autozomálních lokusů:

(p + q)² =	p²	+	2pq	+	q²
	f(AA)		f(Aa)		f(aa)

Spermie ♂	Vajíčka ♀
Spermie ♂	p ~ f(A)	q ~ f(a)
p ~ f(A)	p² ~ f(AA)	pq ~ f(Aa)
q ~ f(a)	pq ~ f(Aa)	q² ~ f(aa)

Souhrn frekvencí v zygotách:

AA: P ́= p²
Aa: H ́= pq + qp = 2pq
aa: Q ́= q²

Důkaz HWE
		Frekvence zygot (potomstvo)
páření	frekvence páření (rodičů)	AA	Aa	aa
AA x AA	P²	1	0	0
AA x Aa	2PH	1/2	1/2	0
AA x aa	2PQ	0	1	0
Aa x Aa	H²	1/4	1/2	1/4
AA x aa	2HQ	0	1/2	1/2
aa x aa	Q²	0	0	1
	Celkem v další generaci	P ́	Q ́	R ́

pak:

P ́= P² + 2PH/2 + H²/4 = (P + H /2)² = p²
H ́= 2PH/2 + 2PQ + H²/2 + 2HQ/2= 2(P + H /2)(Q + H /2)=2pq
Q ́= H²/4 + 2HQ/2 + Q² = (Q + H /2)² = q²

Za předpokladu platnosti podmínek HWE je frekvence homozygotů AA (P ́ u potomků) p², frekvence aa (H ́) je q² a frekvence heterozygotů Aa (Q ́) je 2pq.

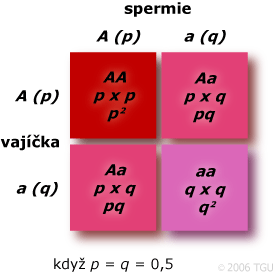
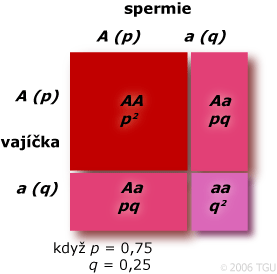
HWE: p = q = 0,5 HWE: p = 0,75

Lze určit frekvenci alely u potomků:

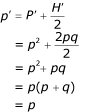Toto odvození dokazuje, že za Hardy-Weinbergovy předpokladů, frekvence alel a genotypů zůstávají stejné napříč generacemi. To znamená, že mendelistická dědičnost nemění sama o sobě frekvence alel. Tato situace se nazývá Hardy-Weinbergova rovnováha (HWE).

Pokud se genotypové frekvence změnily beze změny frekvence alel, pak se frekvence genotypů vrátí na hodnoty za HWE za jednu generaci náhodného páření.

Jestliže evoluční síly změní frekvence alel, pak nová HWE nastane s genotypovými frekvencemi, odpovídajícími novým frekvencím alel (nové p a q tvoří p², 2pq a q²), opět za jednu generaci náhodného páření.

Když p = 0,75 a q = 0,25 a je vyhověno HW podmínkám rovnováhy, pak genotypové frekvence jsou stále p², 2pq a q², které v tomto případě budou mít hodnoty 0,526, 0,375 a 0,062. Hardy-Weinbergova rovnováha může nastat pro jakékoliv frekvence alel. Genotypová rovnováha může nastat, i když je jedna alela fixována (p = 1,0 a p²= 1; q = 0,0 a 2pq = 0,0 a p²= 0,0).

Příklad:

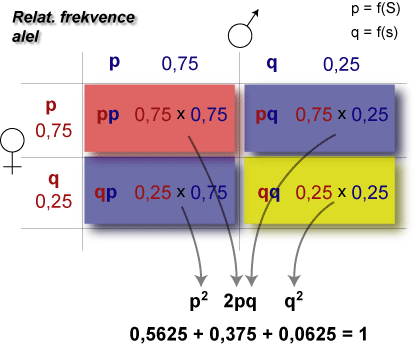
odvození HWE

Jedna frekvence alel může v různých populacích mít různé frekvence genotypů. Ale jen jedna populace je v genetické rovnováze, neboť její frekvence genotypové odpovídají frekvencím rovnice genetické rovnováhy p²+ 2pq + q² = 1. Z četnosti alel nelze vypočítat četnosti genotypů, protože jedné četnosti alel mohou odpovídat různé četnosti genotypů.

p (A)	q (a)	p² (AA)	2pq (Aa)	q² (aa)
0,80	0,20	0,60	0,40	0,00
0,80	0,20	0,61	0,38	0,01
0,80	0,20	0,64	0,32	0,04
0,80	0,20	0,70	0,20	0,10
0,80	0,20	0,75	0,10	0,15
0,80	0,20	0,80	0,00	0,20

Graf níže ukazuje frekvence všech tří genotypů za HWE na lokusu se dvěma alelami pro všechny možné frekvence alel. Tento graf umožňuje pochopit velkou škálu základních konceptů v genetice populací. Tento graf popisuje také stav, kdy je frekvence heterozygotů maximální, když p = q = 0,5. Jestliže a je recesivní alela a frekvence q je malá, pak efekt alely a v populaci je malý, protože většina alel a se nachází v heterozygotech.

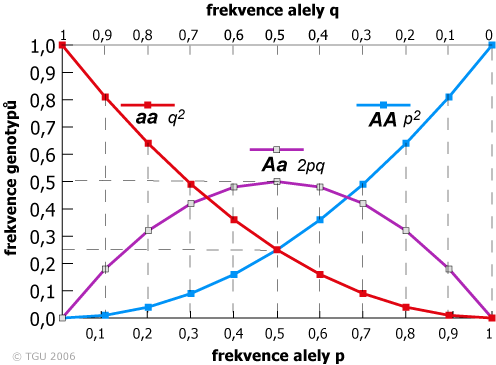
Graf HWE

Rovnovážný stav pro různé frekvence alel. Všimněte si, že čím nižší četnost alely, tím větší je její výskyt v heterozygotech:

p (A)	q (a)	p² (AA)	2pq (Aa)	p² (aa)	p² + 2pq	2pq:q²
0,99	0,01	0,9801	0,0198	0,0001	0,9999	198:1
0,95	0,05	0,9025	0,0950	0,0025	0,9975	38:1
0,90	0,10	0,81	0,18	0,01	0,99	18:1
0,80	0,20	0,64	0,32	0,04	0,96	8:1
0,70	0,30	0,49	0,42	0,09	0,91	4,7:1
0,60	0,40	0,36	0,48	0,16	0,84	3:1
0,50	0,50	0,25	0,50	0,25	0,75	2:1
0,40	0,60	0,16	0,48	0,36	0,64	1,3:1
0,30	0,70	0,09	0,42	0,49	0,51	0,86:1
0,20	0,80	0,04	0,32	0,64	0,36	0,5:1
0,10	0,90	0,01	0,18	0,81	0,19	0,22:1

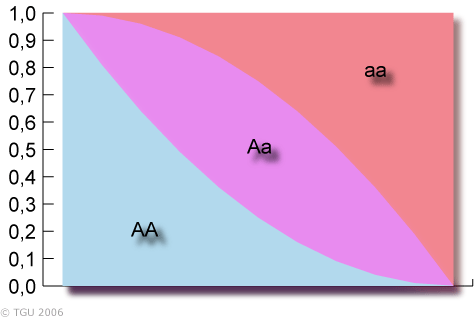
Graf HWE 2

Princip HW rovnováhy má tři hlavní vlastnosti:

frekvence alel předpovídají (určují) frekvence genotypů
v rovnováze se frekvence alel a genotypů nemění z generace na generaci
rovnováha je dosažena za jednu generaci náhodného páření

Testování Hardy-Weinbergovy rovnováhy

Rovnovážný genetický stav v populaci nastává, když platí konkordátní rozložení genotypů, vycházející ze základní rovnice genetické rovnováhy:

Populace je v genetické rovnováze, když frekvence genotypů pozorovaných P (skutečných) se statisticky neliší od frekvencí genotypů za genetické rovnováhy O (očekávané). Na vyhodnocení se používá statistický test dobré shody - (chí kvadrát) test:

kde P značí pozorované počty v každé genotypové třídě, O očekávané počty ve stejných genotypových třídách a naznačuje, že hodnoty jsou sečteny za všechny genotypové třídy.

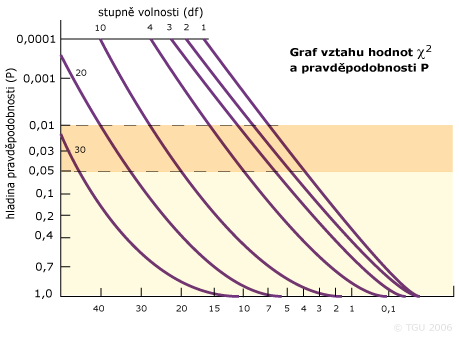
Vypočítaná hodnota se porovnává s tabulkovou hodnotou pro příslušnou pravděpodobnost (95 a 99%) a stupně volnosti. Stupně volnosti pro se zjistí podle: df = počet tříd dat - počet parametrů odhadovaných z dat - 1 = n - p - 1. V případě lokusu se dvěma genotypy a třemi genotypy bude hodnota df = 3 - 1 - 1 = 1.

Graf chi-kvadrát

Příklad:

Byly určeny počty genotypů SS = 66, FS = 20 a F = 14.

Je třeba určit relativní frekvence alel:

p = (2 x 66 + 20)/200 = 0,76
q = (2 x 14 + 20)/200 = 0,24

Dosazením těchto frekvencí alel do členů rovnice HWE získáme očekávané relativní frekvence genotypů. Vynásobením počtem jedinců v populaci získáme očekávané počty genotypů za genetické rovnováhy. Dosazením do vzorce pro zjistíme jeho hodnotu.

Stupně volnosti pro gen se třemi genotypy a dvěma alelami je df = 3 - 1 - 1 = 1. Tabulkové hodnoty:

Tabulkové hodnoty chí kvadrátu
Hladina významnosti	Stupně volnosti
Hladina významnosti	1	2	3	4	5
0,05	3,84	5,99	7,81	9,48	11,07
0,01	6,35	9,21	11,34	13,27	15,08

~ Je shoda mezi pozorovanými a očekávanými četnostmi a H₀ se nezamítá. Pak populace pro daný lokus je v genetické rovnováze.

~ Je průkazný rozdíl mezi pozorovanými a očekávanými četnostmi a H₀ se zamítá. Pak populace pro daný lokus není v genetické rovnováze.

Aktualizováno: 03.02.2015