Jednoduché souhrnné statistiky

• Genetická data populace mohou být vyjádřena jako frekvence (četnosti) alel a genotypů.
• Každý gen má nejméně dvě alely (diploidní organizmy).
• Součet všech frekvencí alel v populaci může být považován za charakteristiku populace (genofond).
• V populaci mohou být frekvence alel různých genů velmi odlišné.
• Dvě populace stejného biologického druhu nemusí mít stejné frekvence genotypů a alel.

Frekvence alel a genotypů

Genetická variabilita odhalená genetickými markery může být kvantifikována mnoha způsoby. Hlavními mírami jsou frekvence alel a genotypů. Z četnosti genotypů lze následně stanovit četností genové (přesněji alelové). Slovo frekvence v genetice populací vyjadřuje podíl, takže frekvence dané alely či genotypu je jednoduše jejím podílem ze všech alel nebo genotypů daného lokusu v populaci. Někdy se termín frekvence genové a frekvence alel zaměňují, což není správné, protože dochází ke zmatení. Geny se neliší ve frekvencích, alely ano.

Rozlišují se frekvence absolutní, počty případů (velká písmena) a frekvence relativní (malá písmena). Velikost populace se značí N, a počet alel u diploidních organizmů je roven 2N. Sledujeme-li jeden lokus se dvěma alelami, označené A a a, pak se obvykle pro jejich frekvence používají symboly p a q. Protože frekvence (poměry) musí být rovny 1, pak:

p + q = 1

p = 1 - q

Tyto rovnice jsou velmi jednoduché, ale jsou velmi důležité pro počítání frekvencí alel. Genotypové frekvence se obvykle označují písmeny d, h a r a jejich součet také musí být roven 1.

Genofond populace nelze zatím studovat přímo, ale pomocí četností genotypů, které se vyskytují v populaci. Z četnosti genotypů lze následně stanovit četností alelové.

Výpočet frekvencí genotypů

Genotypy	Absolutní frekvence	Relativní frekvence
AA	D
Aa	H
aa	R
Součet	D + H + R = N	d + h + r = 1

Výpočet frekvencí alel

Alely	Absolutní frekvence	Relativní frekvence
A	P = 2D + H
a	Q = 2R + H
Součet	P + Q = 2N	p + q = 1

Genetická struktura různých populací člověka v rámci jednoho genu (MN krevní skupiny)

Populace	Frekvence genotypů (%)			Frekvence alel
	MM	MN	NN	M	N
Eskymáci (Grónsko)	83,48	15,64	0,88	0,913	0,087
Indiáni v USA	60,00	35,12	4,88	0,776	0,224
Běloši v USA	29,16	49,38	21,26	0,540	0,460
Černoši v USA	28,42	49,64	21,94	0,532	0,468
Ainiové v Japonsku	17,86	50,20	31,94	0,430	0,570
australští domorodci	3,00	29,60	67,40	0,178	0,822

Př.

Předpokládejme populaci s 400 jedinci. Zastoupení jednotlivých genotypů (jedinců s určeným genotypem) je: AA = 165, Aa = 190 , aa = 45. Pozorované počty alel tedy jsou:

A: P = 2 x 165 + 190 = 520

a: Q = 2 x 45 + 190 = 280

Celkový počet ale ve výběru je 2 x 400 = 800. Pak lze odhadnout p a q z absolutních frekvencí alel:

f(A): p = 520/800 = 0,65

f(a): q = 280/800 = 0,35

a platí že p + q = 1

Nejběžnější výpočet relativních frekvencí alel je výpočet z relativních frekvencí genotypů:

f(AA): d = 165/400 = 0,4125

f(Aa): h = 190/400 = 0,4750

f(aa): r = 45/400 = 0,1125

Pak relativní frekvence alel z relativních frekvencí genotypů:

f(A): p = 0,4125 + 0,4750/2 = 0,65

f(a): q = 0,1125 + 0,4750/2 = 0,35

Pozn.: Pokud jsou obě alely (A, a) náhodně kombinované do genotypů (náhodné páření ve velké populaci), pak lze spočítat očekávané frekvence tří genotypů podle pravidla pro opakované pokusy rozšířením výrazu (p + q)² = p² + 2pq + q². Za předpokladu náhodné kombinace alel do genotypů (při tvorbě zygot) budou očekávané frekvence genotypů:

f(AA): p² = (0,65)² = 0,4225 (x 400 = 169 jedinců)

f(Aa): h = 2 x 0,65 x 0,35 = 0,4550 (x 400 = 182 jedinců)

f(aa): p² = (0,35)² = 0,1225 (x 400 = 49 jedinců)

Tyto frekvence genotypů při náhodné kombinaci alel tvoří koncept Hardy-Weinbergova principu.

 

Parametry a odhady

Je rozdíl mezi skutečnými frekvencemi alel a odhadovanými v populaci. Rozdíl se objeví vždy, když výzkumník dělá závěry o celé populaci z testu náhodně vybraného vzorku z celé populace. To nejlepší, co lze udělat, je odhadovat frekvenci p na základě vzorku a doufat, že vzorek reprezentuje celou populaci. Odhadovaná hodnota p ze vzorku se označuje .

Střední chyba odhadu

Rozdíl mezi parametrem a odhadem je důležitý, protože rozdílné vzorky mohou mít rozdílné hodnoty odhadu frekvence alely z důvodu, že sourozenci se mohou lišit rozdílnou segregací a také náhodností opakování výběru. Odhad frekvence alely se může chovat jako opakující se pokusy za předpokladu, že alely jsou vybírány náhodně, jedna po druhé z velmi velké populace. Měli-li bychom soubor s 800 vybranými alelami a skutečná frekvence alely p = 0,65, pak vysvětlení opakovanými pokusy naznačuje, že všechny možné závěry 800 pokusů mají pravděpodobnosti dané postupně členy rozšíření (0,65 + 0,35)⁸⁰⁰. Toto binomické vyjádření představuje, že při procesu náhodného výběru je třeba počítat s variancí v odhadu z jednoho výběru 800 alel k dalšímu.

Pokud není hodnota p blízká nule nebo jedničce, je vhodnější aproximace k binominálnímu rozložení (p + q)ⁿ, kde n je počet vybraných alel. Čím je n větší, tím se distribuce přibližuje tvaru zvonovité křivky, tedy normální distribuci. Stupeň, kterým hodnoty jsou rozloženy kolem střední hodnoty, závisí na směrodatné odchylce:

,

kde . Jestliže vybírání a odhady p by byly opakovány mnohokrát ve stejné populaci, pak by se očekávalo, že hodnoty budou rozděleny symetricky kolem p podle směrodatné odchylky:

• přibližně 68 % odhadů 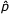leží v intervalu 1 směrodatná odchylka p
• přibližně 95 % odhadů 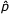leží v intervalu 2 směrodatné odchylky p
• přibližně 99,7 % odhadů 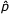leží v intervalu 3 směrodatné odchylky p

Jinými slovy, u 32 % odhadů se dá očekávat, že se budou lišit od skutečné hodnoty p více než 1s, 5 % více než 2s a pouze 0,3 % více než 3s. Tuto situaci dobře zobrazuje následující obrázek.

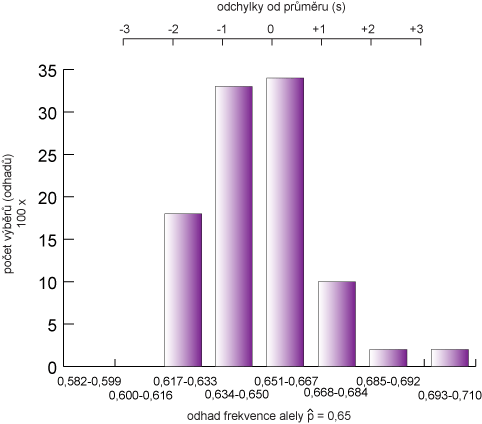
V grafu je zobrazena situace, kde je odhad získán ze 100 opakování experimentu výběrem 800 alel z velké populace, kde byla aktuální frekvence p = 0,65. Kdyby se zkombinovaly průměry ze všech 100 opakování (80000 pozorování) získali bychom = 0,6492. Tato hodnota se již velmi blíží skutečné hodnotě p. Směrodatná odchylka z dat je s = odmocnina [(0,65 x 0,35)/800]= 0,017. Očekávané hodnoty v rozmezí p (1, 2, 3)s jsou:

• s : interval od (0,633 - 0,650) do (0,651 - 0,667), což je 33 a 35 pozorování v každém intervalu (teoreticky 34 v každém intervalu)
• 2s : interval od (0,617 - 0,633) do (0,668 - 0,684), což je 18 a 10 pozorování v každém intervalu (teoreticky 13,5 v každém intervalu)
• 3 s : vyskytovali se 4 jedinci jen v horním intervalu nad 0,685 (teoreticky 2,5 v každém intervalu)

Odhady a jejich směrodatné odchylky jsou často zapisovány jako , nebo 0,65 0,017 v tomto případě. Odhady mohou být také zapsané pomocí konfidenčních intervalů, které vyjadřují míru jistoty, že skutečná hodnota parametru leží v určitém specifickém intervalu. Nejvíce používaný konfidenční interval je 95% konfidenční interval, definovaný jako interval (- 2s, + 2s). U 95% opakovaných výběrů se očekává, že se jednotlivé odhady budou vyskytovat v rozmezí 2s, kolem skutečného průměru a zahrnuje pravou hodnotu parametru p. V našem případě = 0,65, s = 0,017 a 95% konfidenční interval je 0,616 - 0,684.