Aplikace matematiky
Robert Mařík
16. listopadu 2009
Cílem tohoto dokumentu je ukázat některé praktické aplikace matematiky. Příklady
se snažím volit tak, aby byly jednoduché a srozumitelné i pro neodborníky v
dané oblasti. Proto zde například ekonomové nenajdou nějaké hluboké aplikace
matematiky v ekonomii – snažím se o volbu příkladů, u kterých nejsou pro
pochopení problému nutné žádné hluboké znalosti jiných oborů. Snad vám
tyto příklady praktického použití pomohou při pochopení toho, co je z látky,
kterou vás učím (nebo učíme) podstatné a co si máte odnést – ne vzorečky na
derivování (i když ty také – minimálně pro úspěšné složení zkoušky), ale spíš
hlavní smysl derivací, integrálů a dalších pojmů, s nimiž v matematice se
setkáváme.
Dokument vzniká postupně. Pokud sem náhodou zasurfujete a napadne vás
nějaká pěkná aplikace, která tu chybí, můžete mi o tom dát vědět například
mailem.
1 Populárně naučné prezentace
Kromě detailnějších matematických modelů zde naleznete i populárně naučné
prezentace o užitečnosti matematiky pro řešení zajímavých nebo praktických
problémů
2 Lineární algebra
- Většinu procesů v přírodě modelujeme pomocí diferenciálních rovnic, často
lineárních. Někdy linearita přirozeně vyplyne z povahy problému, někdy
lineárně aproximujeme nelineární jevy (viz níže), protože s nelineárními
rovnicemi si zatím dost dobře neumíme poradit. Přitom při řešení
diferenciálních rovnic často využíváme právě lineární algebru, ač se jedná
o oblast matematiky, které je diferenciálnímu počtu poměrně vzdálená.
Stačí však hledat stacionární řešení a úloha diferenciálního počtu se zcela
přirozeně promění v úlohu lineární algebry. Protože lineární algebra obsahuje
mocný aparát poměrně nenáročný na početní operace (nejsou zde žádné
derivace, integrály, logaritmy a jiné zrůdnosti) snažíme se někdy pomocí
aparátu lineární algebry aproximovat řešení nějaké diferenciální rovnice.
3 Derivace
Na derivaci pohlížíme dvojím způsobem - jednak “fyzikálně” jako na rychlost změny
dané veličiny a jednak “geometricky”, jako na směrnici tečny ke grafu funkce.
(Mimochodem – derivace je asi nejsilnějším argumentem pro užitečnost pojmu limita,
protože je definována právě pomocí limity.)
Derivace je veličinou udávající rychlost změny jiné veličiny.
- Pokud kráčím v noci pod lampou, můj stín roste když se od lampy vzdaluji.
Roste tento stín stále stejnou rychlostí, nebo roste zpočátku rychle a pak
pomaleji? Derivace nám na tento problém dají odpověď.
- Stín míče který padá volným pádem vedle lampy se pohybuje. Čím je míč
níže, tím je stín blíž k patě lampy a pohybuje se pomaleji, přestože rychlost
samotného míče se vlivem volného pádu zvyšuje. Jak rychle se tedy tento
stín pohybuje? Odpověď najdeme pomocí derivací.
- Derivaci je možno použít k řešení problému samočištění jezer (samovolné
vyplavování nečistot z jezera tím, že přitéká čistá a odtéká znečištěná voda), či k
modelování protékání nečistot soustavou jezer.
- Jedná se o sestavení diferenciální rovnice, či soustavy diferenciálních
rovnic – tyto rovnice je nutno vyřešit, chceme-li vědět, jak rychle bude
proces probíhat a kdy se značištění dostane na nějakou přijetalnou
hodnotu.
- Hledáme-li však ustálené řešení, ke kterému proces konverguje, stačí
nám vyřešit soustavu lineárních rovnic (bez derivací).
Derivaci je možno použít k hledání stavů systému, které jsou v určitém
smyslu optimální.
- Snažíme-li se dostat proti proudu řeky z bodu A do bodu B, musíme plavat
(či plout s plavidlem) dostatečně rychle, aby nás nestrhával proud, ale ne
příliš rychle, abychom se brzo nevyčerpali (nespotřebovali mnoho paliva a
nezavařili stroje). Je vhodné znát optimální rychlost, která umožní se do cíle
dostat s vynaložením minimální energie.
- Chceme-li z kulatiny vyříznout nosník čtvercového průřezu, který se co
nejméně prohýbá, nesmíme nosník vyřezat ani příliš nízký, ani příliš úzký.
Měl by mít optimální rozměry.
Derivace je prostředkem k popisu vlastností křivek (směrnice tečny).
- Tečna je nejlepší lineární aproximace pro nelineární funkci. Je tak možno
složitější formule nahradit za určitých okolností formulemi jednoduššími.
- Počítání ideální váhy pomocí BMI není zrovna jednoduché pro
výpočty zpaměti. Pokusíme se vzorec využívající BMI aproximovat tak,
abychom si mohli svoji ideální váhu vypočítat zpaměti.
- Kinetická energie tělesa je rozdíl celkové energie E = mc2 a klidové energie
E = m0c2.
- Podle tohoto vzorce však kinetickou energii počítá jen šílenec
nebo fyzik zabývající se relativistickou fyzikou. Většina populace
použije vzorec
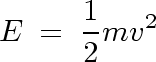 , který je lineárním přiblížením
relativistického vzorce.
, který je lineárním přiblížením
relativistického vzorce.
- Anglická verze tohoto dokumentu je obohacena o využití vyšších
derivací a Taylorova polynomu pro nalezení prvních opravných
členů, sloužících v případě, kdy klasický vzorec pro kinetickou
energii začíná selhávat (objekt se pohybuje relativně vysokou
rychlostí), ale ještě nechceme či necítíme potřebu využít plně
relativistického vzorce.
- Křivka táhnutí je křivka popisující trajektorii objektu taženého jiným
objektem.
- Soubor obsahuje animace v Javě. Aby fungovaly, otevřete soubor v
Adobe Readeru a nepoužívejte alternativní prohlížeče PDF.
- Na podobné myšlence je založena i křivka pronásledování, kde jeden
pohybující se objekt (zajíc) je sledován jiným objektem (psem) tak, že
pes běží z boku rychlostí větší než zajíc a v každém okamžiku směřuje
k zajíci. Uplatnění - samonaváděcí střely (fuj!).
- V textu odvodíme rovnici křivky tak, že najdeme její derivaci a křivku
pak najdeme integrováním.
- Zavěšené mosty jsou lehké a elegantní konstrukce, je potřeba je však postavit tak,
aby síla, která napíná nosné lano, přirozeně směřovala vždy ve směru tohoto lana.
Přitom záleží, jestli lano nese pevnou vodorovnou vozovku, nebo jestli se jedná o
lanový most, jaký známe z filmů o Indiana Jonesovi.
- U prvního typu mostu sestavíme rovnici pro derivaci křivky popisující
tvar nosného lana a křivku najdeme integrováním.
- U druhého typu mostu sestavíme pro hledanou křivku diferenciální
rovnici, kterou je nutno vyřešit.
- Zajímavost: Pomocí těchto výsledků lze postavit oblouk, který je
elegantně štíhlý a přesto dostatečně pevný – oblouk v Saint Louis.
Parciální derivace hrají stejnou úlohu jako derivace obyčejné, ale pro funkce
více proměnných.
- Nepřímo měřenou veličinou rozumíme veličinu, jejíž velikost stanovím tak,
že změřím jiné veličiny (např. M, l, r, φ), a hledanou veličinu vypočtu
pomocí nějakého vzorce (např.
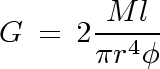 ). Přitom mě zajímá, jaký
mají nepřesnosti při měření vliv na celkovou nepřesnost, se kterou stanovuji
hledanou veličinu G – zejména se zajímám o to, která chyba se projeví
nevýrazněji. Chceme tedy vědět, na které z veličin výsledek závisí silněji.
). Přitom mě zajímá, jaký
mají nepřesnosti při měření vliv na celkovou nepřesnost, se kterou stanovuji
hledanou veličinu G – zejména se zajímám o to, která chyba se projeví
nevýrazněji. Chceme tedy vědět, na které z veličin výsledek závisí silněji.
- Předpovídáme-li z teorie lineární závislost y = ax + b mezi veličinami x a y
a naměříme-li konkrétní hodnoty x a y, zpravidla se nestane, aby všechny
body [x,y] ležely na stejné přímce. Metoda nejmenších čtverců umožňuje
minimalizovat chyby měření a proložit co nejlépe přímku souborem bodů v
rovině. Odvození vzorců pro tuto metodu je vlastně hledání extrémů funkce
dvou proměnných a používáme přitom parciální derivace.
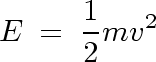 , který je lineárním přiblížením
relativistického vzorce.
, který je lineárním přiblížením
relativistického vzorce.
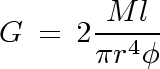 ). Přitom mě zajímá, jaký
mají nepřesnosti při měření vliv na
). Přitom mě zajímá, jaký
mají nepřesnosti při měření vliv na