This article is under construction.
Video presentation
Most of my articles on calculators are just a support to the video presentation of that calculator. The video for this calculator will be prepared on April 2016. Meanwhile you may enjoy the prelimiary attempt here.
Diehl DS18 calculator

This is the Diehl DS 18 calculator. The calculator is a close model to the Diehl KR 15 introduced in a separate article. There are only few differences. The model DS does not have back transfer to the input register (missing R in the name of the model) and has a register which allows to sum up the results - a version of mechanical memory (the letter S in the name of the model). With this device someof the computations can be performed easily and faster than on other calculators.
The mechanical memory

Here we describe some applications of the summation register. Suppose that the user has to fill in the following table.
| No. | Items | Price per one item | Price |
|---|---|---|---|
| 1. | $3$ | $\$121$ | ... |
| 2. | $4$ | $\$213$ | ... |
| 3. | $12$ | $\$96$ | ... |
| 4. | $7$ | $\$126$ | ... |
| Total price | ... |
The user of the calculator has to multiply the number of items and the price per one item to get the price in each row and then sum up all the prices to get the total price. Without the summation register the poor user had two options:
- either to mutltiply the pairs of numbers together and clear the output register after each computation
- or to mutltiply the pairs of the numbers without clearing the output register.
With the first approach the user has to note the results (the price in each row) and reuse them in the final computation wheh he sums the partial prices together. This could be source of errors, if he or she rewrites a number with a typo. With the second method the danger of an error is smaller, since we need not to make notes and reuse them to get the final result. On the other hand, using the second method the machine operator does not see the particular prices in each row, but just the total price.
With the summation register the user evaluates the product (price in the first row) and then transfers to the sum register. The result register is cleared after this operation. Then he or she proceeds in the same way with all the rows. Each particular product appears in the output register and then it is added to the summation register. When the last product is added to the summation register, this register shows the total price.
The lever used to transfer the output register to the summation register is marked with the plus sign in a circle. The following actions are performed when the lever is pushed.
- The number from the output register is added to the memory. Both output register and counter are cleared. It the lever on the right of the summation register is in minus position, then the output register is subtracted and the lever is returned to the plus position.
- The keyboard is cleared or is not cleared depending on the position of the associated lever just besides the button for clearing the keyboard.
- The carriage is moved to the initial position (leftmost position).
The button on the left of the register has been designed to reset the memory register to zero. There is also some lever behind, but I do not understand the purpose of that lever. The scheme of the memory (see the Literature below) also mentions a button in the front which can be used to transfer the number from the memory back to the output register (for division etc). However, something like this seems not to be present on my model.
Under the cover
In the showcase you can enjoy the beauty under the cover. The calculator came very nice and clean inside. No throughout cleaning was necessary. But this does not mean that it worked. Enjoy the beauty of the machine first and the have a look to the restoration story.
A bit of math never harms
You may enjoy the long input where you can enter numbers up to the 9 digit in length.
Definition: A zeroless pandigital number without redundant digits (ZPN) is the number which arises as a permutation of digits 1,2,3,4,5,6,7,8 and 9.
- There is no ZPN such that nine-multiple of this number is again a ZPN.
- The unique ZPN such that eight-multiple of this number is another ZPN is $123456789$, really $$8 \times 123456789 = 987654312$$
- There are only 24 ZPN such that seven-multiple of this number is another ZPN, the smallest of them is $123456789$, the largest is $138976452$ and we have $$7 \times 123456789 = 864197523$$ and $$7 \times 138976452 = 972835164$$
- The number $123456789$ is ZPN which can be multiplied by 2, 4, 5, 7 or 8 and we get again ZPN.
- The largest ZPN such that its multiple is again ZPN is $493827156$ and we have $$2 \times 493827156 = 987654312$$
- If you multiply $987654321$ by $45$, you get the number which contain only one digit different from $4$ $$ 45 \times 987654321 = 44444444445. $$ The same multiple of the reversed number has a similar property $$ 45\times 123456789=5555555505. $$ Another funny multiple of $987654321$ is $99$-multiple. It is a palindrom which contains only two digits different from the others $$ 99\times987654321=97777777779 $$
- There are two consecutive multplies of $123456789$ which are both pandigital without redundant digits (i.e. a permutation of the digits from $0$ to $9$). One such a pair is $$61\times 123456789=7530864129$$ and $$62\times 123456789=7654320918.$$ Other numbers $n$ with the property that both $n\times 123456789$ and $(n+1)\times 123456789$ are a permutation of all ten digits are $16$, $22$, $25$, $31$, $34$, $43$ and $52$.
My restoration story


The calculator came blocked. Like the brother of this calculator, Diehl KR 15, I succeeded to unblock by some (partly random partly organized) pushing the levers by the screwdriver and moving the motor by the hand. The motor worked, but the calculator got blocked again and again. The suspicion was, that the the motor runs too fast, perhaps problems with speed regulation. This proved to be the case and after fixing the problems with electricity, all the basic functionality has been restored.
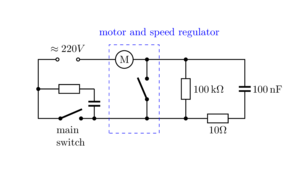
The electric circuit is on the picture. The calculator is protected by some sort of LRC filter attached to the main socket with 220V AC. The solenoid in this part burned and I removed this part without replacement. I hoped, it is not vital for basic function and can be replaced later by a convenient universal net filter. Further you can see that the main switch is in the series with the motor and a speed regulator (another switch mounted directly on the motor with the on/off state regulated by the rotation of the motor).
The main switch is protected by a component (probably RC filter) which burned in my calculator after a short while. I proceeded in the same way as with the input filter: I removed this component as not vital and if the calculator will work, I wil use some modern RC filter (or equivalent and much cheaper option: just a capacitor and resistor). Note that if the capacitor in this part has a short circuit inside, the curcuit is never disconnected. The motor is always on and never stops. On the other hand, if the capacitor is interrupted, the switch is not protected and may produce sparks.
The switch at the speed regulator is also protected by the RC filter. As before, if the capacitor has a short circuit inside, the switch is never off and the speed regulation does not work. This was my case: the high speed of the motor blocked the calculator also after very simple computation. Moreover, the gears got shock from fast move and ruthless bump caused into deformation if fine mechanics inside.
Parallel to the RC filter at the speed regulator you can find a resistor of high resistance, which does not allow to jump the current to zero, but keeps it on certain positive value and protects the motor from too steep jumps in the power management.
The resistors used in the circuit can hardly go wrong, I hope. But all the other parts burned with a lot of smoke and stink. Unfortunately, no two parts went to the component heaven simultaneously. I had to disassemble the calculator and rebuild electric after destroying each single component.
Now I am sure, that if I will repair similar Diehl calculator in future, the first thing will be to rebuild the hole electric circuit and replace old components by their modern versions. If I would do this when I got the calculator from the current article, I would avoid a lot of smoke and odor from burned components and also I would avoid severe shocks of the fine mechanics inside suffering from high speed when the speed regulator was out of order. These shocks had some consequences on the mechanical part and these problems could be prevented.
Literature
- Diehl KR 15 on another part of this site
- Patent DE 1124742 for the mechanical memory.
- Scheme of the mechanical memory.
Robert Mařík, March and April 2016





