Extremalni ulohy

5 Extremální úlohy

Motivace (tři typy extremálních úloh pro funkce více proměnných). Předpokládejme, že funkce $ \displaystyle f$ je spojitá a je definována v bodě $ \displaystyle (x_{0},y_{0})$, který je buď vnitřním nebo hraničním bodem definičního oboru. Bude nás zajímat, kdy jsou funkční hodnoty v bodě $ \displaystyle (x_{0},y_{0})$ ”co největší”, tj. kdy bude platit

\[ f(x_{0},y_{0}) > f(x,y)\quad \text{pro $(x,y)\neq (x_{0},y_{0})$}, \]

(5.1)

případně, kdy bude platit

\[ f(x_{0},y_{0})\geq f(x,y). \]

(5.2)

Pokud platí první z nerovností, říkáme, že funkce $ \displaystyle f$ má v bodě $ \displaystyle (x_{0},y_{0})$ ostré maximum a u druhé z nerovností říkáme, že funkce má v bodě $ \displaystyle (x_{0},y_{0})$ neostré maximum. Přitom musíme důkladně specifikovat, co přesně těmito nerovnostmi rozumíme, tj. pro která $ \displaystyle (x,y)$ musí nerovnost platit. Tím se budou jednotlivé druhy maxim lišit. V praxi má smysl rozeznávat tři druhy extremálních úloh, které jsou postupně uvedeny v následujících definicích.

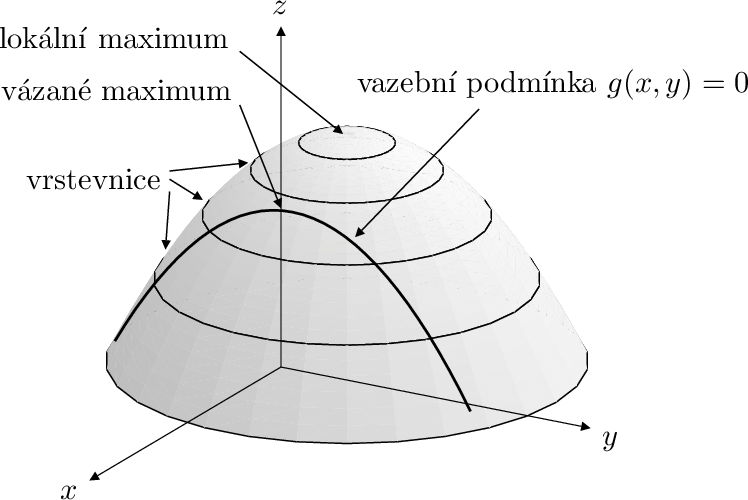
Definice 5.1 (lokální maximum). Je-li bod $ \displaystyle (x_{0},y_{0})$ vnitřním bodem definičního oboru a nerovnost (5.1) (případně (5.2)) platí pro všechna $ \displaystyle (x,y)$ z nějakého okolí bodu $ \displaystyle (x_{0},y_{0})$, říkáme, že funkce má v bodě $ \displaystyle (x_{0},y_{0})$ ostré lokální maximum (případně lokální maximum).

Definice 5.2 (absolutní maximum). Je-li funkce definovaná na předem zadané množině $ \displaystyle M$ a platí-li nerovnost (5.1) (případně (5.2)) pro všechna $ \displaystyle (x,y)\in M$, říkáme, že funkce má v bodě $ \displaystyle (x_{0},y_{0})$ ostré absolutní maximum (případně absolutní maximum) na množině $ \displaystyle M$.

Definice 5.3 (vázané maximum). Uvažujme další předem zadanou spojitou funkci dvou proměnných $ \displaystyle g :\mathbb{R} ^{2}\to \mathbb{R}$, která splňuje $ \displaystyle g(x_{0},y_{0}) = 0$, tj. bod $ \displaystyle (x_{0},y_{0})$ leží na vrstevnici $ \displaystyle g(x,y) = 0$ grafu funkce $ \displaystyle g$. Rovnici této vrstevnice

\[ g(x,y) = 0 \]

(5.3)

budeme nazývat vazební podmínkou. Platí-li nerovnost (5.1) (případně (5.2)) pro všechna $ \displaystyle (x,y)$ z nějakého okolí bodu $ \displaystyle (x_{0},y_{0})$, která splňují vazební podmínku (5.3), říkáme, že funkce má v bodě $ \displaystyle (x_{0},y_{0})$ ostré vázané lokální maximum (případně vázané lokální maximum) vzhledem k vazební podmínce (5.3).

Definice 5.4 (lokální, absolutní a vázané minimum). Změníme-li směr nerovností (5.1) a (5.2), obdržíme podobně (ostré) lokální minimum, (ostré) absolutní minimum na množině $ \displaystyle M$ a (ostré) vázané lokální minimum při vazební podmínce (5.3).

Věta 5.1 (absolutní extrémy na kompaktní množině, Weierstrassova věta). Spojitá funkce má na kompaktní množině absolutní maximum a absolutní minimum.

lok´aln´i maximum z

v´azan´e maximum vazebn´i podm´inka g(x,y) = 0

vrstevnice

y

x

Obrázek 1.1: Jednotlivé typy extrémů funkce dvou proměnných.

Poznámka 5.1 (geometrická interpretace). Geometricky graf funkce dvou proměnných zpravidla chápeme jako plochu v trojrozměrném prostoru. Geometrická interpretace jednotlivých typů extrémů je potom následující.

Ostré lokální maximum je takové místo na grafu funkce, které má nejvyšší funkční hodnotu ve srovnání s body z nejbližšího okolí⁹ .
Uvažujme jenom tu část grafu, jejímž kolmým průmětem do roviny $ \displaystyle z = 0$ (tj. do roviny obsahující osy $ \displaystyle x$ a $ \displaystyle y$) je právě množina $ \displaystyle M$. Ostré absolutní maximum na množině $ \displaystyle M$ odpovídá bodu, který má nejvyšší funkční hodnotu ve srovnání se všemi ostatními body uvažované části grafu¹⁰ .
Uvažujme jenom body na grafu funkce $ \displaystyle f$, které splňují vazební podmínku (5.3). Tyto body vytvoří křivku na grafu funkce $ \displaystyle f$ a tato křivka¹¹ prochází podle předpokladů bodem $ \displaystyle (x_{0},y_{0})$. Vázané ostré lokální maximum při vazební podmínce (5.3) je takové místo na grafu funkce, které má nejvyšší funkční hodnotu ve srovnání s těmi body z nejbližšího okolí, které leží na uvažované křivce¹² .
Interpretace neostrých extrémů je stejná, připouštíme navíc, že se mohou vyskytovat body, mající stejné funkční hodnoty, jako je příslušné maximum.

Poznámka 5.2 (derivace jako nutná podmínka existence lokálních extrémů). V diferenciálním počtu funkcí jedné proměnné platí poučka, že funkce nemá lokální extrém v bodě, v jehož okolí je rostoucí nebo klesající. Podezřelými body pro existenci lokálních extrémů jsou tedy pouze body, kde je derivace nulová, nebo kde derivace neexistuje. Analogické pravidlo platí i pro funkce více proměnných, jak uvádí následující věta.

Věta 5.2 (Fermatova). Jestliže funkce $ \displaystyle f(x,y)$ má v bodě $ \displaystyle (x_{0},y_{0})$ lokální extrém (ostrý nebo neostrý), pak každá parciální derivace, která v tomto bodě existuje, je nulová.

Definice 5.5 (stacionární bod). Bod $ \displaystyle (x_{0},y_{0})$ z definičního oboru funkce $ \displaystyle f$, ve kterém platí

\[ f'_{x}(x_{0},y_{0}) = 0 = f'_{y}(x_{0},y_{0}). \]

(5.4)

se nazývá stacionární bod funkce $ \displaystyle f$.

Poznámka 5.3 (důsledek Fermatovy věty). Lokální extrém tedy může nastat buď ve stacionárním bodě, nebo v bodě, kde alespoň jedna z parciálních derivací neexistuje. Z těchto ”kandidátů” navíc můžeme vyloučit ty, pro které některé parciální derivace neexistují a z těch co existují je alespoň jedna nenulová.

Poznámka 5.4 (stanovení typu lokálního extrému). V ryze praktických případech někdy poznáme z povahy úlohy, že ve stacionárním bodě je extrém a jaký. Například pokud z formulace úlohy je zřejmé, že funkce má nějaké lokální minimum a pokud vyjde jediný stacionární bod, je zřejmé, že lokální minimum je v tomto bodě¹³ . U funkce jedné proměnné jsme věděli, že ve stacionárním bodě je buď lokální maximum, minimum nebo inflexní bod a dokázali jsme mezi jednotlivými alternativami rozlišit pomocí monotonie¹⁴ nebo pomocí druhé derivace¹⁵ . U funkcí dvou proměnných umíme rozhodnout o tom, zda a jaký lokální extrém ve stacionárním bodě nastává, pomocí druhých derivací, což je uvedeno v následující větě.

Věta 5.3 (test pomocí druhé derivace). Nechť bod $ \displaystyle (x_{0},y_{0})$ je stacionárním bodem funkce $ \displaystyle f$ a nechť funkce $ \displaystyle f$ má spojité všechny parciální derivace druhého řádu v okolí tohoto bodu. Označme symbolem $ \displaystyle H$ následující determinant

\[ H(x_{0},y_{0}) = \left \vert \array{ f''_{xx}(x_{0},y_{0})& f''_{xy}(x_{0},y_{0}) \cr f''_{xy}(x_{0},y_{0})& f''_{yy}(x_{0},y_{0})\cr } \right \vert . \]

Nastane právě jeden z následujících případů

$ \displaystyle H > 0$ a $ \displaystyle f''_{xx} > 0$. Potom má funkce $ \displaystyle f$ v bodě $ \displaystyle (x_{0},y_{0})$ ostré lokální minimum.
$ \displaystyle H > 0$ a $ \displaystyle f''_{xx} < 0$. Potom má funkce $ \displaystyle f$ v bodě $ \displaystyle (x_{0},y_{0})$ ostré lokální maximum.
$ \displaystyle H < 0$. Potom funkce $ \displaystyle f$ nemá v bodě $ \displaystyle (x_{0},y_{0})$ lokální extrém.
$ \displaystyle H = 0$. Nelze rozhodnout o existenci a kvalitě lokálního extrému pomocí druhých derivací. Může nastat kterýkoliv z výše uvedených případů.

Definice 5.6 (Hessián). Matice uvedená v předchozí větě se nazývá Hessova matice a její determinant se nazývá Hessián.

Poznámka 5.5 (lokální extrémy funkce více než dvou proměnných). Všechny výše uvedené poznatky lze snadno zobecnit i na funkce $ \displaystyle 3$ a obecně $ \displaystyle n$ proměnných. Výjimkou je v tomto směru pouze předchozí věta, která je v případě funkcí více než $ \displaystyle 2$ proměnných znatelně složitější.

Poznámka 5.6. Všimněte si, že Věta 5.3 je nepoužitelná v případě, že některá z parciálníchderivací neexistuje. Rozhodnout v takovém případě o existenci lokálního extrému je obecně velice obtížný úkol. Při řešení takového úkolu opět nepříjemně pocítíme skutečnost, že zde nemáme jednu pěknou vlastnost, která nám v podobných případech pomáhala u funkce jedné proměnné – totiž monotonii.

Poznámka 5.7 (stanovení lokálních extrémů funkce dvou proměnných).

Nalezneme parciální derivace funkce $ \displaystyle f$.
Vyřešíme soustavu dvou rovnic pro stacionární body.
Nalezneme druhé derivace funkce $ \displaystyle f$.
Rozhodneme pomocí Hessiánu pro každý stacionární bod individuálně, zda a jaký v něm nastává lokální extrém.
Body, v nichž nelze podle předchozího kroku rozhodnout a body, v nichž neexistuje alespoň jedna z prvních parciálních derivací, vyšetřujeme individuálně.

Poznámka 5.8 (vázané lokální extrémy funkce dvou proměnných). Předpokládejme, že z vazební podmínky (5.3) lze explicitně vypočítat buď $ \displaystyle y =\varphi (x)$, nebo $ \displaystyle x =\psi (y)$. Uvažujme nejprve první případ.

Dosadíme vztah $ \displaystyle y =\varphi (x)$ do funkce $ \displaystyle f(x,y)$ a studujeme funkci $ \displaystyle f(x,\varphi (x))$, která je již funkcí jedné proměnné.
Nalezneme lokální extrémy této funkce jedné proměnné postupem známým z diferenciálního počtu funkce jedné proměnné.
Je-li bod $ \displaystyle x_{0}$ lokálním extrémem funkce $ \displaystyle f(x,\varphi (x))$, je bod $ \displaystyle (x_{0},\varphi (x_{0}))$ vázaným lokálním extrémem stejného typu funkce $ \displaystyle f(x,y)$ při vazební podmínce (5.3).

Pokud nelze z vazební podmínky vypočítat $ \displaystyle y$, ale lze vypočítat $ \displaystyle x =\psi (y)$, postupujeme analogicky.

Dosadíme vztah $ \displaystyle x =\psi (y)$ do funkce $ \displaystyle f(x,y)$ a studujeme funkci $ \displaystyle f(\psi (y),y)$, která je již funkcí jedné proměnné $ \displaystyle y$.
Nalezneme lokální extrémy této funkce jedné proměnné.
Je-li bod $ \displaystyle y_{0}$ lokálním extrémem funkce $ \displaystyle f(\psi (y),y)$, je bod $ \displaystyle (\psi (y_{0}),y_{0})$ vázaným lokálním extrémem stejného typu funkce $ \displaystyle f(x,y)$ při vazební podmínce (5.3).

Jsou i vazební podmínky, které nesplňují výše uvedené předpoklady. V těchto případech nejčastěji používáme postup využívající Lagrangeových multiplikátorů (možno nalézt v odborné literatuře).

Poznámka 5.9 (vázané lokální extrémy funkce tří proměnných). Předpokládejme, že hledáme extrém funkce tří proměnných $ \displaystyle f(x,y,z)$ při vazební podmínce $ \displaystyle g(x,y,z) = 0$. Předpokládejme, že z vazební podmínky lze vyjádřit jednu z proměnných pomocí ostatních, nechť je to například $ \displaystyle z$. Lze tedy $ \displaystyle g(x,y,z) = 0$ přepsat do tvaru $ \displaystyle z =\varphi (x,y)$. Dosadíme-li tento vztah do funkce $ \displaystyle f$, obdržíme funkci $ \displaystyle f(x,y,\varphi (x,y))$, která je funkcí dvou proměnných $ \displaystyle x$a $ \displaystyle y$. Nalezneme lokální extrémy této funkce. Je-li $ \displaystyle (x_{0},y_{0})$ takovým lokálním extrémem, je bod $ \displaystyle (x_{0},y_{0},\varphi (x_{0},y_{0}))$ vázaným lokálním extrémem stejného typu funkce $ \displaystyle f(x,y,z)$ při vazební podmínce $ \displaystyle g(x,y,z) = 0$.

Poznámka 5.10 (absolutní extrémy funkce dvou proměnných). Mějme zadánu hladkou funkci $ \displaystyle f$ definovanou na kompaktní množině $ \displaystyle M$.

Nejprve vyšetříme vnitřek množiny $ \displaystyle M$ – nalezneme všechny lokální extrémy funkce $ \displaystyle f$ ležící uvnitř množiny $ \displaystyle M$. Pouze v těchto vnitřních bodech může funkce nabývat absolutního extrému. Toto budou první ”kandidáti” na absolutní extrém.
Vyšetříme hranici množiny $ \displaystyle M$. Zpravidla je nutné, rozdělit tuto hranici na několik částí. Každou část hranice vyjádříme příslušnou rovnicí, každá taková rovnice bude vazební podmínkou. Postupně hledáme vázané lokální extrémy při těchto vazebních podmínkách. Toto budou další ”kandidáti” na body, v nichž může nastat absolutní extrém.
Pokud jsme v předchozím kroku hranici množiny $ \displaystyle M$ rozdělili na více částí, přidáme ke ”kandidátům” i body, kde se jednotlivé části hranice setkávají.
V každém bodě, který jsme pomocí některého z předchozích kroků zařadili mezi ”kandidáty” na absolutní extrém vypočteme funkční hodnotu. Z vypočtených funkčních hodnot (bude jich zpravidla konečně mnoho) vybereme největší a nejmenší — tyto hodnoty odpovídají absolutnímu maximu a absolutnímu minimu funkce $ \displaystyle f$ na množině $ \displaystyle M$.

Věta 5.4 (Bolzanova). Nechť $ \displaystyle f$ je funkce dvou proměnných spojitá na otevřené souvislé množině $ \displaystyle M\subseteq \mathbb{R}^{2}$ a nechť pro některé $ \displaystyle A$, $ \displaystyle B\in M$ platí $ \displaystyle f(A)f(B) < 0$, tj. nechť se $ \displaystyle f(A)$ a $ \displaystyle f(B)$ liší znaménkem. Pak existuje bod $ \displaystyle C\in M$ s vlastností $ \displaystyle f(C) = 0$.