![]()
Případy, kde jeden ze dvou alternativních jevů je možný během každého čísla pokusů. Aplikováním binomické věty, můžeme rychle vypočítat pravděpodobnost jakékoliv specifické sady jevů mezi velkým počtem potenciálních jevů. Např., v rodině jakékoliv velikosti můžeme vypočítat pravděpodobnost jakékoliv kombinace mužského či ženského potomka: v rodině o pěti dětech lze vypočítat pravděpodobnost čtyř dětí jednoho pohlaví a jednoho dítěte druhého pohlaví atd.
Binomická věta: (a + b)2 = 1 , kde a a b jsou pravděpodobnosti dvou alternativních jevů a n je počet pokusů. Pro každou hodnotu n má binomická věta svůj charakter.
| n | dvojčlen | rozvinutý dvojčlen |
| 1 | (a + b)1 | a + b |
| 2 | (a + b)2 | a2 + 2ab + b2 |
| 3 | (a + b)3 | a3 + 3a2b + 3ab2 + b2 |
| 4 | (a + b)4 | a4 + 4a3b + 6a2b2 + 4ab3 + b4 |
| 5 | (a + b)5 | a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 |
| n | (a + b)n |
an, an-1b, an-2b2, an-3b3,
… bn neboli:
|
Numerické koeficienty předcházející každému výrazu lze snadno určit pomocí Pascalova trojúhelníku:
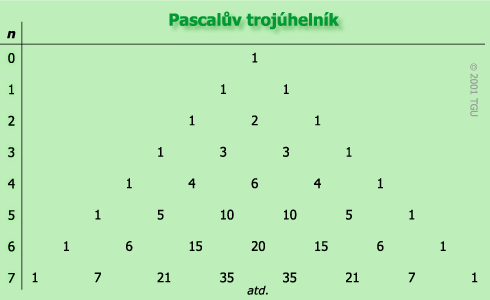
Použitím této metody lze rozčlenit například:
(a + b)7 = a7 + 7a6b + 21a5b2 + 35a4b3 + 35a3b4 + 21a2b5 + 7ab6 + b7
a = chlapec = ½ b = dívka = ½ Pak určíme odpovídající členy v rozvinutém dvojčlenu, kde n = 4: (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 Každý člen, mocnitel nad a reprezentuje počet chlapců a mocnitel nad b pak počet dívek. Takže přesné vyjádření pravděpodobnosti je: P = 6a2b2 = 6(½)2(½)2 = 6(½)4 = 6/16 = 3/8 Pravděpodobnost, že rodiny o 4 dětech budou mít dva chlapce a dvě dívky je 3/8. |
Pro určení početního koeficientu pro jakoukoliv sadu mocnitelů
(chceme-li znát pravděpodobnost určité kombinace ve skupině určitého
rozsahu) může být
aplikován
jednoduchý vzorec: ![]() ,
,
kde n je celkový počet jevů; s je počet kolikrát se jev a stane; t je počet kolikrát se jev b stane; PA , PB jsou pravděpodobnosti příslušných jevů; ! je faktoriál (5! = 5.4.3.2.1 = 120; 0! = 1). Tedy n = s + t.
Použitím vzorce, určeme pravděpodobnost u rodiny se sedmi dětmi, kde bylo 5 chlapců a 2 dívky. Pak s = 5, t = 2 a n = 7. Doplníme i 5 případů jevu A a 2 případy jevu B. V rodinách se sedmi dětmi, průměrně, je 21/128 předpovězeno, že mají 5 chlapců a 2 dívky. |
V rodině, kde oba rodiče mají normální pigmentaci se narodilo albinotické dítě. Tzn. že oba rodiče museli být heterozygoti v genu pro pigmentaci. Jestliže mají 6 dětí, jaká je pravděpodobnost, že 4 budou normální (A) a 2 budou albíni (B)? Na základě křížení Aa x Aa? A = ¾; B = ¼ |
Využití výpočtu na základě binomické věty je v různých oblastech genetiky, včetně analýzy polygenních vlastností a studiu populační rovnováhy.
Binomické rozdělení objevil i Mendel ve svých štěpných poměrech a je charakteristické právě pro genetickou problematiku. Popřemýšlejte znovu o Mendelových experimentech a jeho závěrech z tohoto matematického pohledu!
