Vysokorychlostní syntéza proteinů¶
Tento text je zpracován podle knihy Uri Alon: An Introduction to Systems Biology. Pojednává o tom, jak zpětná vazba může ovlivnit produkci proteinu. Ukazuje několik strategií, jak může příroda zajistit, že v případě potřeby je protein syntetizován rychle a v dostatečném množství. Zaměříme se na matematickou stránku věci. Pěkná přednáška autora knihy a jednoho ze klíčových vědců v systémové biologii, moderní vědě, která se touto problematikou zajímá, je k dispozici na Youtube zde.
Uvažujme model syntézy proteinu, který degraduje rychlostí $s(x)=\beta x,$ kde $\beta$ je konstanta, tj. rychlostí úměrnou množství proteinu $x$. To je realistický a měřením potvrzený předpoklad. Kromě toho je protein ještě i syntetizován jiným procesem. Při dosažení rovnováhy mezi degradací a produkcí je jeho úroveň konstantní.
Schopnost řízení syntézy správných proteinů ve správnou dobu je klíčová pro všechny organismy. Pro některé jednodušší organismy je vzájemný řetězec na sebe navazujících reakcí do značné míry zmapován a popsán. Tato spleť reakcí je výsledkem dlouhodobé evoluce, kde náhodné genové mutace změnily chod dosud zavedených věcí. Tyto mutace buď přinesly svému nositeli výhodu a udržely se a rozšířily, nebo naopak přinesly nevýhodu a jejich nositel mutaci dále nešířil, protože nebyl tak úspěšný v reprodukci.
V tomto dokumentu si ukážeme, jak se dá různými strategiemi ovlivnit rychlost, s jakou je v buňce syntetizován protein. Nejedná se o jedinou záležitost, kterou v souvislosti s chemickými reakcemi v buňce studujeme matematickými prostředky. Dalšími problémy jsou například stabilita a robustnost stacionárních stavů. Přístupy jsou jak kvalitativní (může to takto vůbec fungovat?), tak kvantitativní (dostáváme při předpovědích vypočtených z modelů správné numerické hodnoty pro pozorované veličiny?) a v obou přístupech je dovednost modelování pomocí diferenciálních rovnic nezastupitelnou pomůckou.
import matplotlib.pyplot as plt # knihovna pro statické grafy a grafy kreslit sem do zápisníku
%matplotlib inline
import numpy # knihovna pro numerické výpočty
from scipy.integrate import solve_ivp # řešení diferenciálních rovnic
import bokeh.io # knihovna pro kreslení interaktivních grafů
import bokeh.plotting # knihovna pro kreslení interaktivních grafů
bokeh.io.output_notebook() # grafy kreslit sem do zápisníku
colors = ['red','blue','orange','green'] # paleta barev
Produkce konstantní rychlostí¶
Množství proteinu označme $x$ a předpokládejme produkci konstantní rychlostí. Spolu s degradací z předchozího odstavce tedy máme model $$\frac{\mathrm dx}{\mathrm dt}=\alpha - \beta x.$$
Redukce počtu parametrů (nondimenzionalizace)¶
Vhodnou volbou jednotek pro veličinu $x$ je možné docílit toho, že platí $\alpha = \beta.$ Opravdu, rovnici je možno přepsat na tvar $$\frac{\mathrm d x}{\mathrm dt}=\alpha \left(1- \frac{\beta x}{\alpha} \right)$$ a odsud po vynásobení faktorem $\frac \beta\alpha$ $$ \frac{\mathrm d\frac{\beta x}{\alpha}}{\mathrm dt}=\beta \left(1 - \frac{\beta x}{\alpha} \right), $$ což v nových jednotkách $X=\frac {\beta x}\alpha$ vede na rovnici $$\frac{\mathrm d X}{\mathrm dt}=\beta \left(1 - X \right).$$ Tato volba znamená, že množství proteinu měříme v procentech rovnovážného stavu. Vhodnou volbou jednotky času je možné dosáhnout toho, že společná konstanta $\beta$ je numericky rovna jedné. Tuto volbu však dělat nebudeme, protože chceme porovnávat časový průběh pro různé hodnoty konstanty $\beta$. Pro pohodlí se navíc vrátíme k původnímu označení malým písmenem, tj. budeme studovat rovnici $$ \frac{\mathrm d x}{\mathrm dt}=\beta \left(1 - x \right).$$ Toto je rovnice $$ \frac{\mathrm d (x-1)}{\mathrm dt}=-\beta \left(x - 1 \right), $$ tj. rovnice popisující rozklad rychlostí úměrnou množství pro veličinu $x-1$ a řešením je tedy $$x(t)=1-(1-x_0) e^{-\beta t}. $$ Přestože máme k dispozici analytické řešení, vyřešíme si úlohu numericky, abychom mohli poté volit různé rychlosti produkce.
Růstové křivky¶
Nejprve nakreslíme křivky produkce a degradace do jednoho obrázku, abychom dokázali lokalizovat stacionární body.
Křivky pro stejné hodnoty parametru jsou stejnou barvou.
Průsečík křivek stejné barvy je stacionární bod systému při nastavení parametrů daném příslušnou barvou. Všimněte si, že všechny tyto průsečíky jsou nad sebou a každý v jiné výšce. Pro všechny parametry nastává stacionární stav pro stejné množství proteinu $x=1$, ale rychlosti produkce a degradace ve v tomtom stacionárním stavu liší.
Všechna nastavení parametrů vykazují převažující růst pro malé a převažující degradaci pro velké hodnoty $x$. Stacionární body jsou tedy stabilní.
beta = [1,2,3,4] # definice parametrů
alpha = beta # alpha a beta jsou po vhodné volbě jednotek pro x stejné
x = numpy.linspace(0, 2, 100) # definice intervalu pro kreslení růstových křivek
p = bokeh.plotting.figure(title="Křivky produkce a degradce proteinu",
x_axis_label='množství proteinu',
y_axis_label='rychlost produkce a degradace proteinu',
y_range=(0, 5)
# plot_width=1000
)
for i in range(len(beta)): # Cyklus přes parametry
produkce = beta[i]+0*x # Křivka produkce
degradace = beta[i]*x # Křivka degradace
p.line(x,produkce, color=colors[i], legend_label="produkce, alpha=beta=%s"%str(beta[i]), width=3) # Vykreslení křivky produkce
p.line(x,degradace, color=colors[i], legend_label="degradace, alpha=beta=%s"%str(beta[i]), width=3, line_dash='dashed') # Vykreslení křivky degradace
p.legend.click_policy="hide" # Skrývat křivky po kliknutí na legendu
bokeh.plotting.show(p)
Časový vývoj řešení¶
Průběh řešení pro jednotlivé hodnoty parametru u řešení vycházejícího z nulové počáteční podmínky je na obrázku. V praxi nás zajímá, jak rychle bude dosaženo určitého množství proteinu. Tedy vybereme si nějakou hladinu, například $0.6$, a sledujeme, která křivka této hladiny dosáhne jako první a která jako poslední.
tmin, tmax = 0,3 # definice počátečního a koncového časového okamžiku
t = numpy.linspace(tmin, tmax, 1000) # definice intervalu pro kreslení funkcí času
p = bokeh.plotting.figure(title="Množství proteinu jako funkce času",
x_axis_label='čas',
y_axis_label='množství proteinu',
#plot_width=1000
)
beta = [1,2,3,4] # nastavení parametrů
for i in range(len(beta)): # cyklus přes počáteční podmínky
# Vyřešení rovnice dx/dt=beta*(1-x) pro danou počáteční podmínku
sol = solve_ivp(lambda t, x: beta[i]*(1-x), [tmin, tmax], [0], dense_output=True)
reseni=sol.sol(t)[0] # uložení řešení do proměnné
p.line(t, reseni, # vykreslení řešení
color=colors[i],
legend_label="alpha=beta=%s"%str(beta[i]),
width=3
)
p.legend.click_policy="hide" # skrývat křivky po kliknutí na legendu
bokeh.plotting.show(p) # vykreslení řešení
Rychlá produkce je “zaplacena” rychlou degradací¶
Je patrné, že nejrychleji hladina enzymu roste pro nejvyšší hodnotu parametru. Vodorovnou čáru ve výšce $0.6$ protne jako první zelená křivka. Být první je neskutečně důležité, někdy přímo otázka života a smrti. Taková bakterie, která umí rychle produkovat enzym, například umí rychle uniknout z prostředí s nepříznivými životními podmínkami (rychle sestaví proteiny, které vytvoří jakýsi molekulární motor a ten buňku posune na jiné místo) nebo umí rychle začít ukládat v přítomnosti glukózy energii pro budoucí využití. Na druhou stranu, popsaným mechanismem je rychlost je dosažena nejenom rychlou produkcí, ale i rychlou degradací proteinu. Tedy protein se rychle produkuje a rychle rozpadá. Už z laického hlediska se takový postup nezdá být postupem optimálním pro přežití. Je to jako bychom u auta chěli mít možnost okamžitě zrychlit a za tímto účelem udržovali vysoké otáčky motoru, ale abychom jeli rozumnou rychlostí tak bychom brzdili. Tedy bychom současně šlapali na plyn i na brzdu. To rozumný člověk nedělá.
Proteiny ve skutečnosti nejsou rychle odbourávány. Popsaný mechanismus šlapání na brzdu a plyn současně v buněčném světě ve skutečnosti není použit. Životnost proteinu není řádově odlišná od životnosti buňky. Příroda a evoluce by takové plýtvání nepřipustily a namísto toho se k problému rychlé produkce proteinu staví jinak. Použitím zpětné vazby, což je předmětem následující kapitoly.
Vysoká rychlost produkce díky záporné zpětné vazbě¶
Předpokládejme produkci proteinu rychlostí související s množstvím proteinu. Jedná se tedy o model $$\frac{\mathrm dx}{\mathrm dt}=f(x) - \beta x,$$ kde $f(x)$ je rychlost produkce. Budeme porovnávat vliv funkce $f(x)$ na rychlost syntézy.
Vhodný tvar funkce $f(x)$ si můžeme vypůjčit například z modelu syntézy kolagenu ze cvičení v předmětu Aplikovaná matematika. Budeme uvažovat funkci která je rozdílem konstanty a třetí mocniny, tj. $$ f(x)=a-bx^3.$$
Redukce počtu parametrů, nondimenzionalizace¶
Vhodnou volbou jednotek pro veličinu $x$ dosáhneme toho, že stacionárním bodem bude $x=1$ (jinými slovy, množství enzymu budeme měřit v procentech rovnovážného stavu). Protože budeme uvažovat stále stejnou rychlost degradace a sledovat jenom vliv funkce $f(x)$, můžeme jednotky času zvolit tak, že $\beta = 1$. Tj. studujeme rovnici $$\frac{\mathrm dx}{\mathrm dt}=f(x) - x,$$ kde $f(1)=1$. Aby byla navíc splněna podmínka $f(1)=1$, budeme uvažovat funkci $$f(x)=\alpha-(\alpha-1)x^3, \quad \alpha \geq 1.$$
Křivky růstu a degradace¶
Funkce $$f(x)=\alpha-(\alpha-1)x^3, \quad \alpha \geq 1$$ je klesající funkce. Rychlost produkce tedy ubývá s množstvím. Toto se nazývá záporná zpětná vazba. Parametr $\alpha$ reguluje sílu této zpětné vazby, čím je vyšší, tím je zpětná vazba výraznější. Vyšší $\alpha$ charakterizuje vyšší hodnotu průsečíku na svislé ose (rychlejší produkci při nulové hladině proteinu) a rychlejší pokles při rostoucí koncentraci. Pěkně to je vidět na následujícím obrázku.
alpha = [1, 2, 3, 4] # Hodnoty parametrů
x = numpy.linspace(0, 2, 100) # Interval pro kreslení růstových křivek
p = bokeh.plotting.figure(title="Křivky produkce a degradce proteinu",
x_axis_label='množství proteinu',
y_axis_label='rychlost produkce a degradace proteinu',
y_range=(0, 4.5),
# plot_width=1000
)
for i in range(len(alpha)): # Cyklus přes parametry
produkce = alpha[i]-(alpha[i]-1)*x**3 # Křivka produkce
p.line(x,produkce, # Vykreslení křivky produkce
color=colors[i],
legend_label="produkce, alpha=%s"%str(beta[i]),
width=3)
degradace = x # Křivka degradace
p.line(x,degradace, # Vykreslení křivky degradace
color='black',
legend_label="degradace, společná pro všechny parametry",
width=3,
line_dash='dashed'
)
p.legend.click_policy="hide" # Skrývat křivky po kliknutí na legendu
bokeh.plotting.show(p) # Vykreslení grafu
Časový průběh řešení modelu¶
Zkusíme si namodelovat průběh řešení modelu pro různé hodnoty parametru.
tmin, tmax = 0, 3 # meze pro čas
t = numpy.linspace(tmin, tmax, 1000) # časový interval na 1000 dílků
p = bokeh.plotting.figure(title="Množství proteinu jako funkce času",
x_axis_label='čas',
y_axis_label='množství proteinu',
#plot_width=1000
)
alpha = [1,2,3,4] # nastavení paramatrů
for i in range(len(alpha)): # cyklus přes hodnoty parametrů
# Vyřešení rovnice dx/dt = alpha - (alpha-1)*x^3 - x pro nulovou počáteční podmínku
sol = solve_ivp(lambda t, x: alpha[i]-(alpha[i]-1)*x**3 - x, [tmin, tmax], [0], dense_output=True)
reseni=sol.sol(t)[0] # uložení řešení
p.line(t, reseni, # vykreslení řešení
color=colors[i],
legend_label="alpha=%s"%str(beta[i]),
width=3
)
p.legend.click_policy="hide" # skrývat křivky po kliknutí na legendu
bokeh.plotting.show(p)
Čím vyšší hodnota koeficientu $\alpha$, tím je počáteční produkce rychlejší a dříve je dosaženo potřebného množství enzymu. Toto se děje při konstantní zpětné vazbě a konstantním stacionárním stavu (všechny rovnice mají člen popsující degradaci ve tvaru $-x$ a stacionární stav $x=1$).
Jupíí, vysoká rychlost produkce i při nízké rychlostí degradace¶
Vidíme, že negativní zpětná vazba příznivě ovlivňuje rychlost syntézy proteinu. Tím je buňce umožněno zareagovat rychle na vnější podmínky, aniž by za to platila cenou rychlé degradace, jako bez zpětné vazby (současně přidávání plynu a brždění). Taková zpětná vazba může být zprostředkována například tím, že protein vstupuje do jiných chemických reakcí, jak jsme například modelovali v rovnici popusující syntézu kolagenu.
Příroda zařadila i do jednoduchých organismů typu buňka takových zpětných vazeb obrovské množství a dlouholetou evolucí vyladila hodnoty parametrů tak, aby potřebné proteiny vznikaly přesně v době, kdy jsou potřeba a aby dostatečně rychle vznikly v potřebné koncentraci. To je zařízeno mutacemi v genech. Chybou v přepise genů například může vznikout zpětná vazba, která do té doby neexistovala. Pokud se projeví jako užitečná, dává svému nositeli evoluční výhodu a šíří se dál. Podobně se během milionů let vyladí parametry této zpětné vazby, například hodnota parametru $\alpha$. Těmito problémy zabývá věda nazývaná systémová biologie. Tato věda prodělala bouřlivý rozvoj v letech okolo roku 2000, kdy byly vyvinuty učinné postupy pro získávání potřebných dat o genech a proteinech a tento rozvoj pokračuje dodnes.
Poznatky, na kterých je založen tento dokument, jsou potvzeny experimentálně. Používá se například vnesení genu způsobujícího světélkování do genetické informace bakterií.
Záporná zpětná vazba pomocí inhibitoru¶
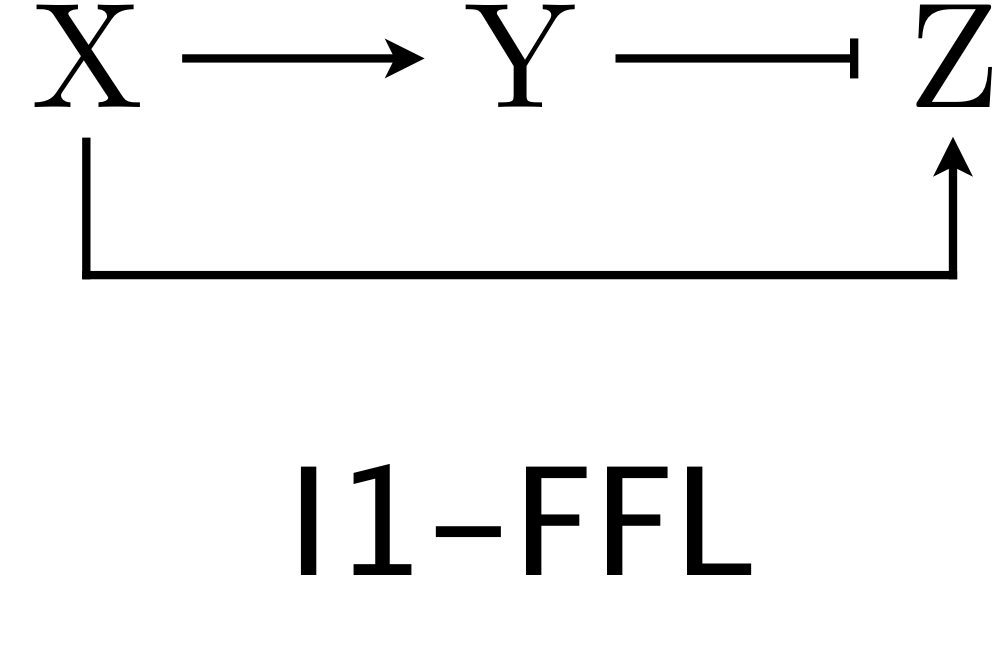(Obrázek z http://be150.caltech.edu/2020/content/lessons/05_ffls.html)
Uvažujme systém chemických reakcí, kdy přítomnost X spustí produkci Y a Z. Přitom Y je inhibitor pro Z a od určité aktivní koncentrace brzdí jeho produkci. Tento řetězec reakcí se vyskytuje často ve schématech reakcí probíhajících v buňce a nazývá se I1-FFL feed-forward loop network motif. S těmito schématy se pracuje podobně jako se součástmi elekrických obvodů, proto se můžeme v češtině na danou strukturu odkazovat jako na I1-FFL obvod.
Matematický model¶
Množství jednotlivých látek budeme vyjadřovat pomocí odpovídajících malých písmen abecedy. Tato množství budeme měřit v násobcích jejich rovnovážného množství. Spuštění reakce je $x(t)=1$ a tedy je látka X přítomna v konstantní koncentraci a nemusíme ji zahrnovat do dynamiky. Množství dalších látek jsou dána rovnicemi $$ \begin{aligned} \frac{\mathrm dy}{\mathrm dt}&=a-by\cr \frac{\mathrm dz}{\mathrm dt}&=f(y)-\beta z. \end{aligned} $$ Pro látku Y tyto rovnice vyjadřují konstantní produkci a degradaci úměrnou množství. Pro látku Z vyjadřují produkci závislou na množství represoru Y a degradaci úměrnou množství Z. Pro jednoduchost budeme volit funkci $f(y)$ ve tvaru přepínače, který při dosažení určitého množství Y přepne rychlost produkce Z na nižší. Tedy $$ f(y)=\begin{cases} r_1 & y<y_{\text{crit}} \cr r_2 & y>y_{\text{crit}}, \end{cases} $$ kde $r_1$ a $r_2$ jsou konstanty, přičemž $r_2<r_1$. Jinýmy slovy, model se chová jako $$ \begin{aligned} \frac{\mathrm dy}{\mathrm dt}&=a-by\cr \frac{\mathrm dz}{\mathrm dt}&=r_1-\beta z \end{aligned} $$ dokud množství $y$ nedosáhne hodnoty $y_{\text{crit}}$ a poté se začne chovat jako $$ \begin{aligned} \frac{\mathrm dy}{\mathrm dt}&=a-by\cr \frac{\mathrm dz}{\mathrm dt}&=r_2-\beta z. \end{aligned} $$ Proměnná $z$ nejprve konverguje k rovnovážné hodnotě $\frac{r_1}{\beta}$ a proměnná $y$ k hodnotě $\frac ab$. Jakmile $y$ vystoupá nad $y_{\text{crit}}$, přepne se chování systému a proměnná $z$ začne konvergovat k hodnotě $\frac{r_2}\beta$. Pokud je $r_1$ vysoké, mohlo se stát, že než bylo syntetizováno dostatečné množství inhibitoru Y, narostlo množství Z nad hodnotu $\frac{r_2}\beta$. Potom bude $z$ k nové rovnovážné poloze klesat. Jedná se vlastně o dvě samostatné rovnice s řešením v exponenciálním tvaru, přičemž jedna rovnice řídí přepnutí druhé rovnice na jinou hodnotu parametrů. Přesto si v numerickém modelu tuto úlohu naformulujeme jako úlohu pro systém, abychom měli otevřenou cestu k dalším modifikacím.
x=1
switch=0.6
def model(t, promenne): # Definice interakce mezi proteiny
global switch
y, z = promenne
a, b, c, beta = 2, 2, 4, 4
b = a
return [a - b*y, c*(1-0.5*numpy.heaviside(y-switch,1)) + - beta*z]
pocatek = [0,0]
tmin, tmax = 0, 3
t = numpy.linspace (tmin,tmax,1000)
reseni = solve_ivp(model, [tmin, tmax], pocatek, dense_output=True )
p = bokeh.plotting.figure(plot_height=300,
plot_width=600,
x_axis_label='čas',
y_axis_label='množství enzymu')
y, z = reseni.sol(t)
p.line(t, y, legend_label='relativní množství y', width=3)
p.line(t, z/z[-1], color='red', legend_label='relativní množství z', width = 3)
p.line(t, 1-0.5*numpy.heaviside(y-switch,1), color='green', legend_label='relativní rychlost produkce z', width = 3)
p.legend.click_policy="hide" # skrývat křivky po kliknutí na legendu
bokeh.io.show(p)
Druhá taktika rozumného zvýšení rychlosti produkce, I1 FFL obvod¶
V obrázku jsou množství látek normována tak, aby rovnovážná koncentrace byla rovna jedné. Látka Y se syntetizuje rychlostí úměrnou chybějícímu množství do rovnovážné koncentrace. Vidíme, že látka Z se může syntetizovat mnohem rychleji, červená křivka má mnohem rychlejší náběh. To je další taktika zrychlení, které používá příroda k tomu, aby řetezec syntézy proteinů fungoval tak, že každý protein je k dispozici v potřebný čas a v potřebném množství. Tuto taktiku je pochopitelně možno kombinovat s taktikou, kterou jsme viděli již v předchozím, se zápornou zpětnou vazbou. Příslušné rovnice a hodnoty parametrů i v tomto případě do systému “zadrátuje” evoluce.
Další využití obvodu I1 FFL¶
Popsanou strukuturu je možné využít nejenom k tomu, aby buňky dokázaly rychle syntetizovat proteiny. Je možné ji využít i k tomu, aby se buňky naučily derivovat (ano, není to překlep) nebo syntetizovat proteiny systémem JIT, just in time. Ale to je povídání zase na jindy. Zatím se můžete podívat, jak I1 FFL obvod umí zajisist, že při smyslovém vnímání reagujeme na relativní nárůst podnětu a nikoliv na absolutní.
Závěr¶
Ukázali jsme tři taktiky vedoucí k rychlé syntéze potřebných látek v buňce. Jednu “nerozumnou” založenou na rychlé produkci a rychlé degradaci, a dvě použitelné v evoluci, založené na zpětné vazbě. Díky zpětné vazbě, která zpomalí produkci při dostatečném množství produktu, je možnost mít rychlý proces syntézy potřebných látek bez požadavku na vysokou rovnovážnou hodnotu nebo na vysokou rychlost odbourávání. Zpětná vazba umožňuje rychlou syntézu proteinů i při udržení nízké hladiny proteinů v rovnovážném stavu a udržení nízké rychlosti jejich degradace. Ukázali jsme si zpětnou vazbu zprostředkovanou rovnicí $$\frac{\mathrm dx}{\mathrm dt}=f(x) - \beta x$$ a také zpětnou vazbu realizovanou I1 FFL obvodem. Zatímco první z nich funguje jenom pro zrychlení produkce enzymů, zpětná vazba založená na I1 FFL obvodu je použitelná i pro geny (viz Alon).
Podobný model jako zde, ale se spojitým zapnutím zpětné vazby namísto skoku, je v online materiálech ke kurzu Design Principles of Genetic Circuits na prestižní univerzitě Caltech (California Institute of Technology).
Literatura¶
U. Alon: An Introduction to Systems Biology: Design Principles of Biological Circuits, 2nd edition, CRC Press, 2019.
Materiály kurzu Design Principles of Genetic Circuits, Caltech, Spring term, 2020. URL http://be150.caltech.edu/2020/content/lessons/05_ffls.html (27.3.2021)