Žebro chladiče, vývoj embrya i radon¶

Budeme studovat jednorozměrnou difuzní rovnici se spotřebiči úměrnými stavové veličině a v homogenním prostředí s lineární materiálovou charakteristikou, tj. rovnici $$\frac{\partial u}{\partial t}=-ku+D\frac{\partial ^2u}{\partial x^2},\tag{1}$$ kde $k$ a $D$ jsou konstanty.

Model odpovídá například rozložení teploty v tyči, kde se teplo předává do okolí rychlostí úměrnou teplotě. Tato úloha je důležitá z technického hlediska, protože modeluje například žebro chladiče v jednodimenzionálním přiblížení, viz Spakovskzy (2007).

V systémové a vývojové biologii tato rovnice popisuje morfogen. Tato úloha je důležitá z hlediska pochopení vývoje zárodku ze shluku stejných zárodečných buněk na buňky jednotlivých tkání. Morfogen je transkripční faktor, který je na určitém místě embrya vyvíjejícího se živočicha, šíří se prostředím a degraduje. Z gradientu kocentrace dvou morfogenů zárodečné buňky poznají svou polohu v embryu. Poznají tím, na buňky jaké tkáně se mají přeměnit. Viz Doležal (2021) a Wartlick(2009). Poměrně podrobně je tato problematika rozebrána v knize Alon (2019) v kapitole 12.4 na příkladu mušky octomilky (Drosophila).

Jiný model, který nás přivede ke stejné rovnici, je model difuze radonu. Tento model je důležitý pro ochranu zdraví, protože radon jako radioaktivní těžký plyn vniká do budov, kumuluje se ve sklepích nebo v přízemí těchto budov. V oblastech se zvýšeným rizikem je jedním z nejzávažnějších spouštěčů rakoviny plic. Jako každý radioaktivní materiál, i radon se rozpadá rychlostí úměrnou množství tohoto prvku. Difuzní rovnice se započítáním konstantních zdrojů (prvky, ze kterých radon vzniká, mají dlouhý poločast rozpadu a na časové škále, na které studujedme změny koncentrace radonu, je jejich množství prakticky konstantní) je $$\frac{\partial u}{\partial t}=P-ku+D\frac{\partial ^2u}{\partial x^2}$$ a pokud uvažujeme asociovanou homogenní rovnici, dostáváme rovnici (1). Více viz Ishimori (2013).

Budeme hledat stacionární řešení, kdy se rovnice (1) zjednoduší na rovnici $$-ku+D\frac{\mathrm d ^2u}{\mathrm d x^2}=0.$$ Jedná se o diferenciální rovnici druhého řádu s konstantními koeficienty. Obecným řešením této rovnice je funkce $$ u=C_1 e^{-\sqrt{\frac{k}D}x}+C_2e^{\sqrt{\frac{k}D}x}.$$ My se budeme snažit tuto rovnici vyřešit společně s okrajovými podmínkami. To se dá udělat i analyticky, pokusíme se však o numerické řešení. Numerické řešení je snadno dosažitelné na počítači a narozdíl od analytického řešení není těžké postup modifikovat i na technicky zajímavější aplikace, například na nehomogenní prostředí a nelineární materiálovou charakteristiku.

Knihovna SciPy vyžaduje přepsat rovnici vyššího řádu na systém rovnic prvního řádu. Naši rovnici je možno přepsat na systém $$\begin{aligned}\frac{\mathrm d u}{\mathrm d x}&=v\cr \frac{\mathrm d v}{\mathrm d x}&=\frac{k}{D}u.\end{aligned}$$ Tento systém budeme řešit pro různé okrajové podmínky a různá nastavení parametrů. Při pořizování počítačového kódu vyjdeme z dokumentace funkce zajišťující hledání řešení okrajové úlohy.

import numpy
from scipy.integrate import solve_bvp
import matplotlib.pyplot as plt

def fun(X, Y):
    global k,D       # konstanty k a D použijeme globální
    u,v = Y          # identifikace komponent řešení
    return numpy.vstack((v, (k)/D*u))  # pravé strany rovnic jako sloupcový vektor

x = numpy.linspace(0, 1, 15)
y = numpy.zeros((2, x.size))
x_plot = numpy.linspace(0, 1, 100)   # interval pro kreslení grafu na 100 dílků

Smíšená okrajová úloha¶

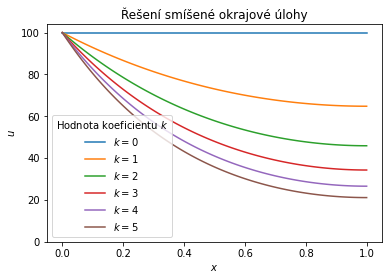
Budeme uvažovat okrajové podmínky $u(0)=100$ a $\frac{\mathrm du}{\mathrm dx}(1)=0.$ Okrajové podmínky vyjadřují, že levý konec je udržován na konstantní teplotě a pravý konec neodevzdává teplo do okolí. Pro systém je můžeme přepsat do tvaru $$\begin{aligned}u(a)-100&=0\cr v(1)&=0.\end{aligned}$$ Pro $k=0$ se jedná o vedení tepla v homogenním prostředí bez spotřebičů a očekáváme konstantní profil. Pro $k>0$ je podél tyče předáváno teplo do okolí a teplota klesá. Podle velikosti koeficientu $k$ klesne teplota na pravém konci hodně nebo málo. Větší hodnota $k$ vede ze zkušeností k rychlejšímu poklesu teploty.

D=1  # Důležitý je podíl k/D. Proto D volíme konstantní a měníme jenom k.

def bc2(Ya, Yb):  # definice okrajových podmínek
    # Ya je řešení v levém krajním bodě
    # Ya[0] je první komponenta tohoto řešení, tj. u
    # v levém bodě je u=100, tj. nuluje se funkce Ya[0]-100
    # Yb je řešení v pravém krajním bodě
    # Yb[1] je druhá komponenta tohoto řešení, tj. v, což je du/dx
    # v pravém bodě je du/dx=0, tj. nuluje se funkce Yb[1]
    return numpy.array([Ya[0]-100, Yb[1]])

for k in (0,1,2,3,4,5):
    sol = solve_bvp(fun, bc2, x, y)     # vyřešení rovnice pro danou hodnotu parametru
    y_plot = sol.sol(x_plot)[0]         # výpočet bodů pro vykreslení řešení
    plt.plot(x_plot, y_plot, label = r"$k=%s$"%k)  # vykreslení řešení
    
plt.xlabel(r"$x$")  # popisky na osách
plt.ylabel(r"$u$")
plt.ylim(0)      # dolní mez na svislé ose
plt.legend(title=r"Hodnota koeficientu $k$")  # legenda, včetně nadpisu
plt.title("Řešení smíšené okrajové úlohy") # nadpis grafu
plt.show()

Dirichletova okrajová úloha¶

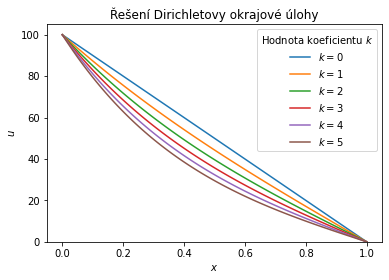
Budeme uvažovat okrajové podmínky $u(0)=100$ a $u(1)=0.$ Tyto podmínky vyjadřují, že oba konce jsou udržovány na konstantní teplotě, každý na jiné. Pro $k=0$ se jedná o vedení tepla v homogenním prostředí a očekáváme lineární profil. Pro $k>0$ je podél tyče předáváno teplo do okolí a teplota klesá rychleji.

D=1

def bc(Ya, Yb):  # Okrajové podmínky
    return numpy.array([Ya[0]-100, Yb[0]])

for k in (0,1,2,3,4,5):
    sol = solve_bvp(fun, bc, x, y)
    y_plot = sol.sol(x_plot)[0]
    plt.plot(x_plot, y_plot, label = r"$k=%s$"%k)
    
plt.xlabel(r"$x$")  # popisky na osách
plt.ylabel(r"$u$")
plt.ylim(0)
plt.legend(title=r"Hodnota koeficientu $k$")
plt.title("Řešení Dirichletovy okrajové úlohy")
plt.show()

Nekonstantní difuzní koeficient¶

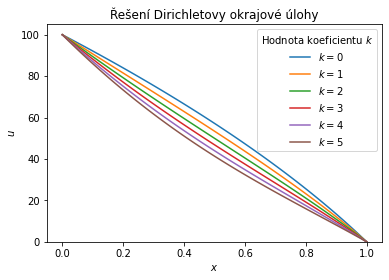
Popsanou analýzu můžeme udělat i s nekonstantním difuzním koeficentem $D$, což by se nám v obecném případě provádělo již hůře. To by odpovídalo vedení tepla v materiálu, jehož ochota vést teplo se mění s teplotou. Například pokud součinitel tepelné vodivosti s teplotou roste, očekáváme při větší teplotě intenzivnější předávání tepla a tedy i menší teplotní rozdíly. Proto by pro velké teploty křivka neměla klesat tak rychle. Vyjde to z modelu? Ten má ve stacionární verzi tvar $$-kT+\frac{\mathrm d }{\mathrm d x}\left(D\frac{\mathrm d T}{\mathrm d x}\right)=0.$$

Soustava rovnic ekvivalentní této rovnici je po označení $u=T$ a $\displaystyle v=D\frac{\mathrm d T}{\mathrm d x}$ ve tvaru $$\begin{aligned}\frac{\mathrm d u}{\mathrm d x}&=\frac 1D v\cr \frac{\mathrm d v}{\mathrm d x}&=ku.\end{aligned}$$

def fun(X, Y):
    global k         # konstantu k použijeme globální
    u,v = Y          # identifikace komponent řešení
    return numpy.vstack((1/(1.2+0.01*u)*v, (k)*u))  # pravé strany rovnic jako sloupcový vektor
    # soucinitel vodivosti roste s teplotou u podle vzorce 1.2+0.01*u

def bc(Ya, Yb):  # Okrajové podmínky
    return numpy.array([Ya[0]-100, Yb[0]])

for k in (0,1,2,3,4,5):
    sol = solve_bvp(fun, bc, x, y)
    y_plot = sol.sol(x_plot)[0]
    plt.plot(x_plot, y_plot, label = r"$k=%s$"%k)
    
plt.xlabel(r"$x$")  # popisky na osách
plt.ylabel(r"$u$")
plt.ylim(0)
plt.legend(title=r"Hodnota koeficientu $k$")
plt.title("Řešení Dirichletovy okrajové úlohy")
plt.show()

Redukce parametrů¶

V modelování reálných dějů hledáme kompromis mezi minimálním množstvím parametrů (snazší interpretace možných chování rovnice) a mezi ponecháním fyzikálního významu všech veličin (snazší interpretace souvislosti mezi matematickým modelem a fyzikální realitou). Například rovnici radonu $$\frac{\partial u}{\partial t}=P-ku+D\frac{\partial ^2u}{\partial x^2}$$ je možné volbou $U=u-\frac Pk$ přepsat do tvaru $$\frac{\partial U}{\partial t}=-kU+D\frac{\partial ^2U}{\partial x^2}$$ a v nových jednotkách je rovnice homogenní a má nulové řešení. Podobně je možné naložit s rovnicí popisující předávání tepla z žebra chladiče do okolí, kde je rychlost ve skutečnosti úměrná teplotě jenom v případě, že okolní teplota je nulová. Je-li okolní teplota $T_0$, měla by rovnice (1) napsaná pro teplotu tvar $$\frac{\partial T}{\partial t}=-k(T-T_0)+D\frac{\partial ^2T}{\partial x^2},$$ což je vzhledem k výše uvedenému skoro ekvivalentní rovnici (1). Přesněji, odpovídá rovnici (1) při volbě $u=T-T_0$.

Literatura¶

Uri Alon: An Introduction to Systems Biology: Design Principles of Biological Circuits, 2nd edition, CRC Press, 2019.
Tomáš Doležal: Vývojová biologie, online https://www.prf.jcu.cz/zmb/menu/vyvojova-biologie.html (2.4.2021)
Y. Ishimori, K. Lange, P. Martin, Y.S. Maya, M. Phaneuf: Measurement and calculation of radon releases from NORM residues, Vienna: International atomic energy agency, 2013. ISBN 978–92–0–142610–9. online https://www-pub.iaea.org/MTCD/Publications/PDF/trs474_webfile.pdf (4.4.2021)
Zoltán Spakovskzy: Heat Transfer From a Fin (2007) online https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node128.html (4.4.2021)
Ortrud Wartlick, Anna Kicheva, Marcos González-Gaitán: Morphogen Gradient Formation, Cold Spring Harb Perspect Biol. 2009 Sep; 1(3): a001255. doi: 10.1101/cshperspect.a001255 https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2773637/ (2.4.2021)
SciPy referrence guide, online https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.solve_bvp.html (4.4.2021)