Periodické přemnožování obaleče¶
import matplotlib.pyplot as plt # knihovna pro statické grafy a grafy kreslit sem do zápisníku
%matplotlib inline
import numpy # knihovna pro numerické výpočty
from scipy.integrate import solve_ivp # řešení diferenciálních rovnic
Následující model je model obaleče Choristoneura fumiferana, který periodicky atakuje lesy severní Ameriky. Jeho populace je relativně malá, ale některé roky se velikost populace zvýší tisícinásobně a dokáže zahubit $80$ procent stromů v lese. Tedy prakticky zničit les. Model sestavili dva matematikové (D. Ludwig a D. D. Jones) a jeden ekolog (C. S. Holling), aby nahradili starý počítačový model Canadian Forestry Service, který používal 30 654 proměnných spojených diferenčními rovnicemi. Nový model pracoval jenom se třemi rovnicemi.
Zde si představíme zjednodušenou verzi o jediné rovnici. Princip zjednodušení je v úvaze, že dynamika hmyzu je mnohem rychlejší než dynamika lesa a při sledování pouze populace hmyzu si můžeme dovolit považovat parametry lesa za konstantní. Matematikové mluví o kvazistacionárním přiblížení. Plný model kromě dobrých výsledků podal i objasnění příčiny náhlého masového přemnožení obaleče, ke kterému docházelo přibližně vždy po 35 letech. Původní počítačový model dokázal pouze počítat simulace.
Matematický model¶
Zde představený model je jeden z klasických modelů popsaných v mnoha učebnicích. Můžeme vycházet například z knihy Brauer, Kribs, Dynamical systems for biological modelling, plný text je pro uživatele MENDELU zdarma.
Populaci obaleče je možno modelovat logistickou rovnicí $$\frac{\mathrm dx}{\mathrm dt}=rx\left(1-\frac xK\right)-H\frac{x^2}{x^2+A^2},$$ kde druhý člen na pravé straně charakterizuje vliv predátorů. Jedná se o funkci, která zpomaluje růst, podobně jako lov v modelu s populací vystavené konstantnímu lovu. Protože však predátoři mají určitou hodnotu, nad kterou jsou saturovaní a nestačí brzdit růst populace, je tato funkce ohraničená. Platí $$H\frac{x^2}{x^2+A^2} \leq H.$$ To má dalekosáhlé důsledky. Pro určité hodnoty parametrů může mít pravá strana rovnice pro $x>0$ jeden nebo tři nulové body. Abychom to pěkně viděli i s reálými dopady, nejprve si model zjednodušíme a poté vyřešíme pro různé hodnoty parametrů.
Nondimenzionalizace¶
Pro jednodušší kvalitativní analýza modelu snížíme počet parametrů. Například:
zvolíme jednotku veličiny $x$ tak, aby koeficient $A$ byl roven jedné,
zvolíme jednotku času tak, aby koeficient $H$ byl roven jedné
vytkneme proměnnou $x$.
Model má potom tvar $$\frac{\mathrm dx}{\mathrm dt}=x\left [ r\left(1-\frac xK\right)-\frac{x}{x^2+1}\right].$$ Na pravé straně v hranaté závorce zůstává rozdíl funkce $\frac{x}{x^2+1}$ neobsahující žádný parametr a lineární funkce, se kterou snadno dokážeme manipulovat. Tento model je možné také zapsat ve tvaru $$\frac {\frac{\mathrm dx}{\mathrm dt}}{x}=r\left(1-\frac xK\right)-\frac{x}{x^2+1}$$ a výraz na levé straně, podíl rychlosti růstu a velikosti růstu, interpretujeme jako relativní rychlost růstu.
Numerický model¶
Nakreslíme křivky definované pravými stranami a řešení diferenciální rovnice pro různé počáteční podmínky
xmax = 15
tspan = numpy.linspace(0, 30, 1000)
xspan = numpy.linspace(0, xmax, 100)
x = xspan
count=0
# nastavení parametrů, pro které budeme počítat model
# uspořádané dvojice [r,K]
parametry = [ [0.5,5] , [0.5, 6], [0.5, 7], [0.5, 8], [0.5,10], [0.5,12], [0.6,12] ]
for par in parametry: # cyklus přes různé hodnoty parametrů
fig, axes = plt.subplots(1, 3, figsize=(20,5)) # inicializace a nastavení obrázku, kreslíme tři obrázky vedle sebe
count = count + 1
fig.suptitle('Model %s: Dynamika populace pro r=%s a K=%s.'%(count,par[0],par[1]), fontsize=18)
r, K = par
ax = axes[0] # kreslíme do prvního obrázku
ax.plot(x,r*(1-x/K),color='blue', label='Relativní rychlost rozmnožování') # přímka, růst popualce
ax.plot(x,x/(1+x**2), color='red', label='Relativní rychlost predace') # působení predátorů
ax.set_ylim([0,None]) # osa od nuly
ax.set_title("Růstové křivky I")
ax.set_xlabel("Velikost populace")
ax.set_ylabel("Rychlost růstu")
ax.legend(loc="upper right")
ax = axes[1] # kreslíme do druhého obrázku
ax.set_ylim([0,xmax]) # nastavení rozsahu pro svislou osu
ax.set_xlim([0,0.8]) # nastavení rozsahu pro vodorovnou osu
ax.plot(r*(1-x/K),x, color='blue', label='Relativní rychlost rozmnožování') # přímka v soustavě souřadnic se svislou osou x
ax.plot(x/(1+x**2),x, color='red', label='Relativní rychlost predace') # působení predátorů v soustavě souřadnic se svislou osou x
ax.set_title("Růstové křivky I")
ax.set_ylabel("Velikost populace")
ax.set_xlabel("Rychlost růstu")
ax.legend(loc="upper right")
ax = axes[2] # kreslíme do třetího obrázku
ax.set_ylim(0,xmax) # nastavení rozsahu pro svislou osu
for i in numpy.linspace(0,12,30): # cyklus přes počáteční podmínky
sol = solve_ivp(lambda t, x: r*x*(1-x/K)-x**2/(1+x**2), [tspan[0], tspan[-1]], [i], t_eval=tspan)
ax.plot(sol.t, sol.y[0]) # vykreslení řešení
ax.set_title("Časový vývoj populace")
ax.set_xlabel("Čas")
ax.set_ylabel("Velikost populace")
ax.set_facecolor('#f0f0f0') # šedé pozadí obrázku
None
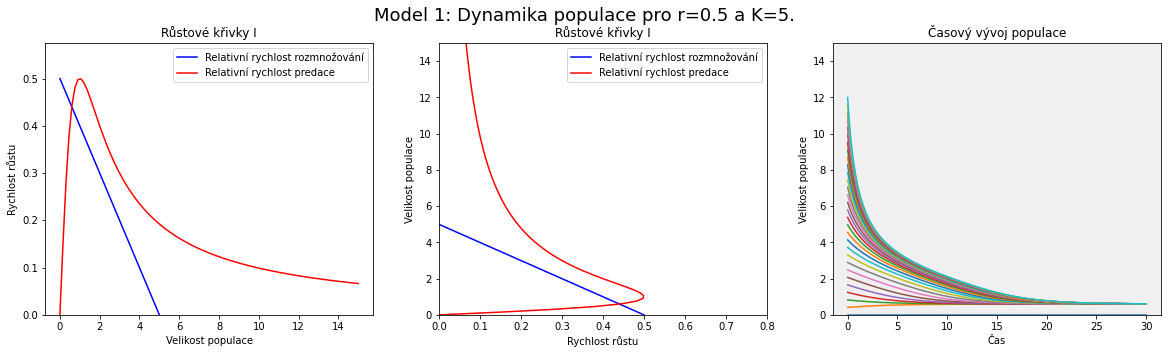
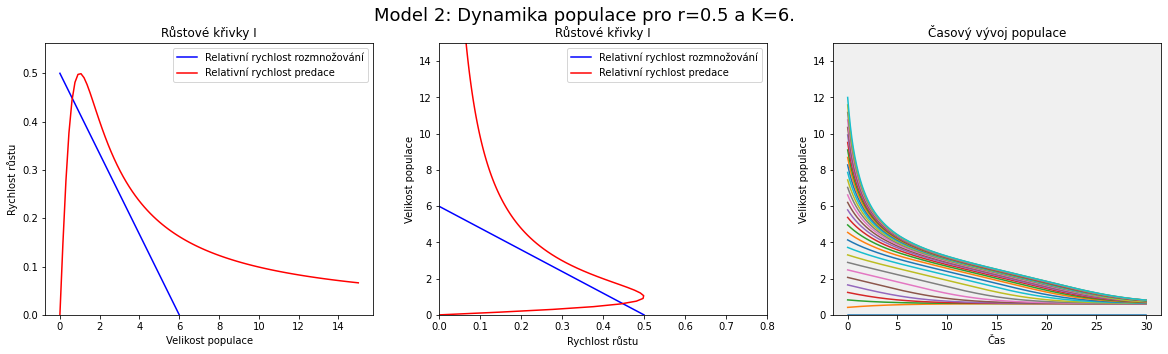
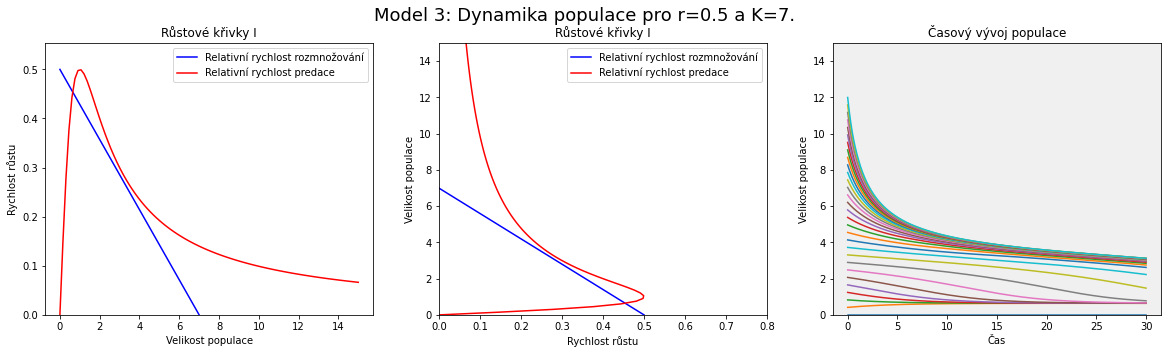
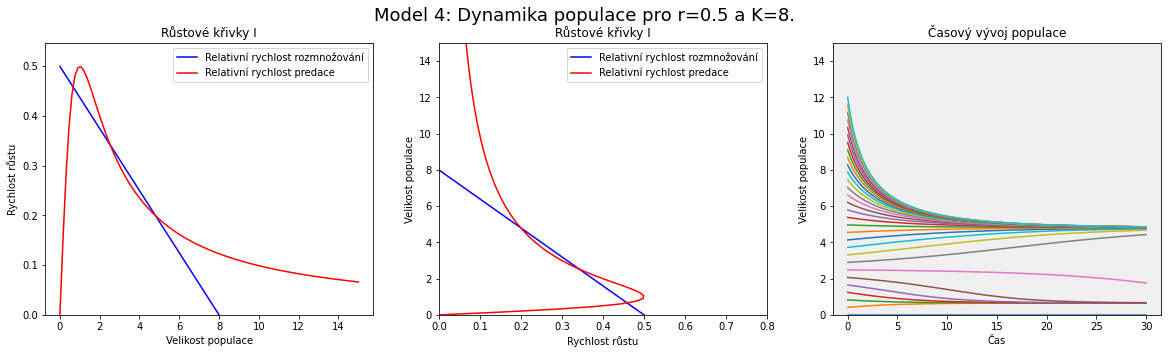
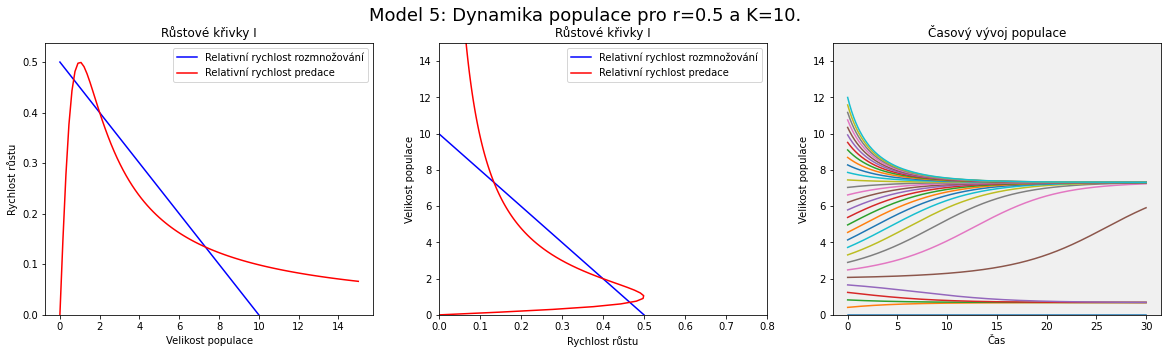
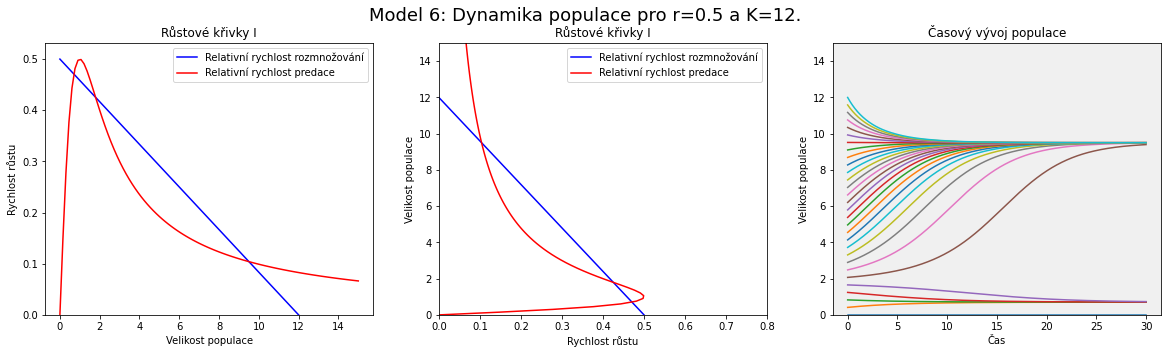
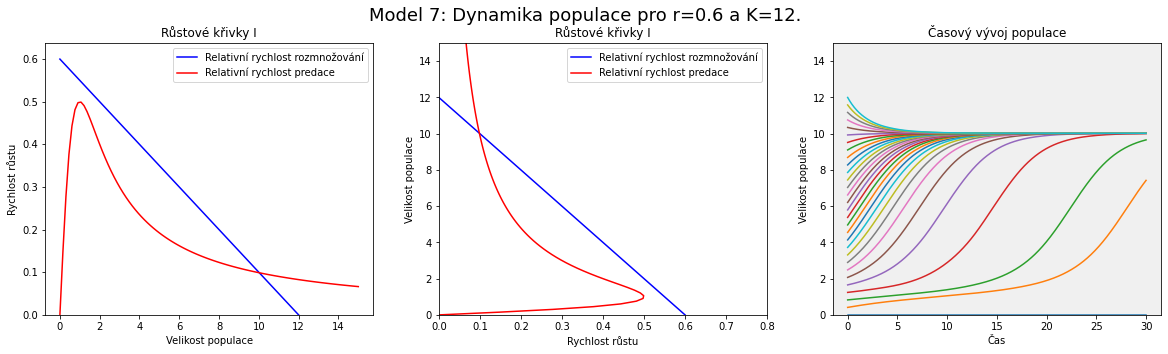
V modelu se postupně zvyšuje nosná kapacita prostředí (roste les) a malinko zvedneme i rychlost rozmnožování (například jsou roky příznivé pro vývoj hmyzu). Z obrázku je patrné, že zásadnější vliv na polohu a počet průsečíků má parametr $K$, nosná kapacita prostředí. To odpovídá místu, kde modrá přímka protíná vodorovnou osu na obrázku nalevo, resp. svislou na obrázku uprostřed.
Pro malé hodnoty (malý les) vidíme jeden průsečík pro malé $x$. Populace obaleče je přítomna, ale v malé míře. S rostoucí hodnotou $K$ se objeví další dva průsečíky, které odpovídají po řadě nestabilnímu a stabilnímu stacionárnímu bodu. Populace obaleče má možnost dalšího stacionárního stavu, ale pro dosažení vyššího stavu by musel překonat bariéru mezi stabilním stavem o malé velikosti populace a nestabilním stavem. I když k různým zakolísáním ve velikosti populace dochází, tak výrazné zakolísání směrem nahoru není pravděpodobné. Jak se však hodnota $K$ dále zvyšuje, je bariéra stále menší. Od určité hodnoty parametru $K$ dokonce nestabilní stav a stabilní stav s nízkou velikostí populace zaniknou a ze třech průsečíků křivek zůstane jenom ten napravo, který odpovídá stabilnímu stavu s vysokou velikostí populace obaleče.
Popsaným mechanismem Brauer a Kirbs vysvětlují situaci s periodickým přemnožováním. S růstem lesa se mění parametry modelu, stacionární body se posunují a populace obaleče se tomu přizpůsobuje. Více stromů znamená vyšší nosnou kapacitu prostředí pro obaleče a predátoři svou činností populaci obaleče udržují na rozumné míře. Pokud však nosná kapacita prostředí dosáhne takové hodnoty, že predátoři jsou nasycení a nestačí populaci redukovat, odpovídá to posunu nestabilního stacionárního bodu pod hodnotu velikosti populace a dojde k přemnožení. Toto přemnožení má devastující účinky pro les.
Matematický model přemnožení kůrovce¶
Dynamika kůrovce je jiná než u obaleče. U obaleče hraje roli rostoucí nosná kapacita prostředí a predace ptáky. Kůrovec nemá významné predátory a jeho přemnožení s nosnou kapacitou tolik nesouvisí. Matematický model jeho dynamiky byl také navržen, viz Křivan. Nahlédnutím do modelu zjistíte, že populace, které jsou ve středu našeho zájmu, jsou rozděleny do několika skupin. Pro každou z těchto skupin jsou definovány procesy, které tuto skupinu obohacují a procesy, které tuto skupinu ochuzují. Výsledkem je soustava rovnic, kterou je možno studovat po matematické stránce tak, jak je uvedeno v článku, nebo je možno ji prozkoumávat numericky. Modely založené na myšlence rozdělení populace na skupiny a sledování rychlosti změn těchto skupin se nazývají kompartmentové modely a jsou velice silným nástrojem pro simulace. Bohužel rostoucí počet skupin dramaticky zvětšuje složitost a odkazuje nás v podstatě pouze právě na numerické simulace. Proto jsou v modelu kůrovce použity triky, které umožní soustavu čtyř rovnic (1) zredukovat na soustavu dvou rovnic (10), kterou je již možné prozkoumat metodami založenými na vlastnostech rovinných křivek (v publikaci o kůrovcovi celostránkový obrázek na straně 30).
Literatura¶
D. Ludwig, D.D. Jones, C.S. Holling: Qualitative analysis of insect outbreak systems: the spruce budworm and forest, Journal of Animal Ecology 47(1): 315–332, February 1978.
Křivan, V., Lewis, M., Bentz, B., Bewick, S., Lenhart, S., Liebhold, A. 2016. A dynamical model for bark beetle outbreaks. Journal of Theoretical Biology 407:25-37. DOI 10.1016/j.jtbi.2016.07.009. Online verze (27.3.2021)
