Konstitutivní zákony¶
Konstitutivní zákony jsou zákony definující vztah mezi stavovou veličinou a jejím tokem. Můžeme si představit například teplotu a tok tepla. Tato představa je nejnázornější, ale mohla by být matoucí, protože teplota je intenzivní veličina. Veličina, která se přesunuje tokem, není teplota, ale energie. Proto si místo toho můžeme představit i něco jiného. Nabízí se například obsah vody v materiálu. Představme si například vodu v prostředí, ve kterém se může pohybovat, ale tento pohyb je pomalý. Nejčastěji si jako konkrétní model představujeme vlhkostní pole ve dřevě, nebo hladinu podzemní vody v půdě. To by pro nás mohly být vhodné materiálové realizace obecných myšlenek.
Tok přenášené veličiny souvisí s tím, jak nerovnoměrně je rozložena tato veličina v prostoru. Pokud je množství veličiny ve všech bodech stejné, k toku nedochází. (V případě teploty, která je intenzivní veličinou, pochopitelně nemluvíme o množství teploty v bodě, ale o teplotě v bodě. U obsahu vody v bodě máme na mysli hustotu tohoto obsahu, tj. obsah vody v jednotce objemu, jednotce plochy nebo jednotce délky, podle dimenzionality úlohy.)
Pokud mají všechny části tělesa stejnou teplotu, nedochází v tělese k toku tepla. Nemůže se část tělesa samovolně ohřát a druhá ochladit.
Pokud mají všechny části tělesa stejný obsah vody, nedochází v tělese k přenosu vody difuzním tokem. Voda se samovolně nezačne koncentrovat v jednom místě více, než v místě jiném.
Pro pochopení souvislosti mezi stavovou veličinou a jejím tokem nejprve musíme mít míru udávající nerovnoměrnost rozložení stavové veličiny v prostoru. To bude veličina měřící intenzitu podnětu, který spouští tok.
Gradient¶
Gradient skalární funkce dvou proměnných $f(x,y)$ je vektorové pole označené $\nabla f$ a definované vztahem $$ \nabla f=\begin{pmatrix}\frac{\partial f}{\partial x}\cr \frac{\partial f}{\partial y}\end{pmatrix}. $$
Gradient skalární veličiny $f$ je vektorová veličina, která vyjadřuje směr a intenzitu maximálního růstu veličiny $f$. Přesněji, výsledkem gradientu je vektor ve směru maximálního růstu veličiny $f$. Délka tohoto vektoru je nárůst veličiny $f$ na intervalu jednotkové délky. Pro rovnoměrně rozloženou veličinu v prostoru (tj. s konstantní hustotou) je gradient nulový. Proto je možné gradient chápat jako míru nerovnoměrného rozložení veličiny v prostoru. Řada fyzikálních dějů probíhá tak, že tato nerovnoměrnost vyvolá proudění, které se snaží tuto nerovnoměrnost vyrovnat. Například teplotní rozdíl vyvolá tok tepla, který se snaží teploty vyrovnat. Rozdíl v koncentracích vyvola difuzní tok, který se snaží vyrovnat koncetnrace. V těchto případech tedy teče teplo do míst s menší teplotou nebo látka podléhající difuzi domíst s menší koncentrací. V praxi nás díky tomuto většinou nezajímá směr maximálního růstu, ale pokles. Pracuje se tedy se záporně vzatým gradientem, $-\nabla f$.
Pokud je například gradient teploty v rovině v bodě $(1,1)$ dán vektorem
$$
\nabla T(1,1)=\begin{pmatrix}1 \cr -2\end{pmatrix}{}^{\circ}\mathrm C \mathrm m^{-1},
$$
znamená to, že v tomto bodě roste teplota ve směru osy $x$ rychlostí $1$ stupeň Celsia na každý metr délky a ve směru osy $y$ klesá rychlostí $2$ stupně Celsia na každý metr délky. Vektor definovaný tímto gradientem má směr doprava dolů (pod úhlem splňujícím podmínku $\tan \varphi = -2$) a délku $\sqrt{(1)^2+(-2)^2}=\sqrt 5\approx 2.2$. To znamená, že maximální nárůst teploty je směrem doprava dolů a tento nárůst je $2.2$ stupně Celsia na každý metr délky.
V následujícím textu něco podobného použijeme pro počítačem vygenerovaná data. Nakreslíme si rozložení teploty a gradient. Všímejme si, že šipky míří vždy směrem, kterým nejrychleji roste teplota, což poznáme podle barev na “termosnímku”. Tento termosnímek můžeme chápat tak, že deska je uprostřed ochlazována na nulovou teplotu. (Ve skutečnosti pouze chladič uprostřed nestačí, závislost by byla logaritmická. Pro rovnoměný pokles teploty směrem do středu je nutné rozmístit po desce chladiče přesně napočítaného výkonu tak, aby pokles byl rovnoměrný. Jak takový výkon napočítat se dozvíme studiem difuzní rovnice a rovnice vedení tepla a praktická realizace takového výpočtu je v kapitole Dvojný integrál. Jiná taktika by byla skládat desku z materiálů různé tepelné vodivosti a tyto vodivosti opět napočítat tak, aby i bez zdrojů teplota klesala směrem ke středu jako lineární funkce vzdálenosti od středu.)
import numpy # knihovna na numerické výpočty (goniomerické funkce, gradient, 2D mřížka a dělení intervalu, ...)
import scipy.integrate # knihovna na vědecké výpočty (integrál)
import matplotlib.pyplot as plt # knihovna na kreslení
def teplota (x,y):
return numpy.sqrt(x**2+y**2)
steps = 51 # hustota mřížky pro kreslení teplotního snímku
ps = 5 # krok na mřížce při kreslení gradientu a toku
y, x = numpy.mgrid[-1:1:steps*1j, -1:1:steps*1j] # mrizka pro kresleni gradientu a barevne mapy funkce dvou promennych
z = teplota(x, y) # výpočet teploty na mřížce
grady, gradx = numpy.gradient(z) # gradient teploty
fig, ax = plt.subplots(1,1, figsize=(20,12)) # inicializace grafiky
## Vykreslení teploty a gradientu teploty
cmap = plt.get_cmap('hot') # nastaveni schema pro barevnou mapu
output = plt.pcolormesh(x, y, z, cmap=cmap, shading='gouraud') # vykresleni barevne mapy pomocí zvolené barevné mapy a vyhlazování přechodů
plt.colorbar(output) # barevný sloupec s hodnotami vedle grafu
plt.quiver(x[::ps,::ps], y[::ps,::ps], gradx[::ps,::ps], grady[::ps,::ps], color='blue') # vykreslení toku
ax.set_aspect(1)
None
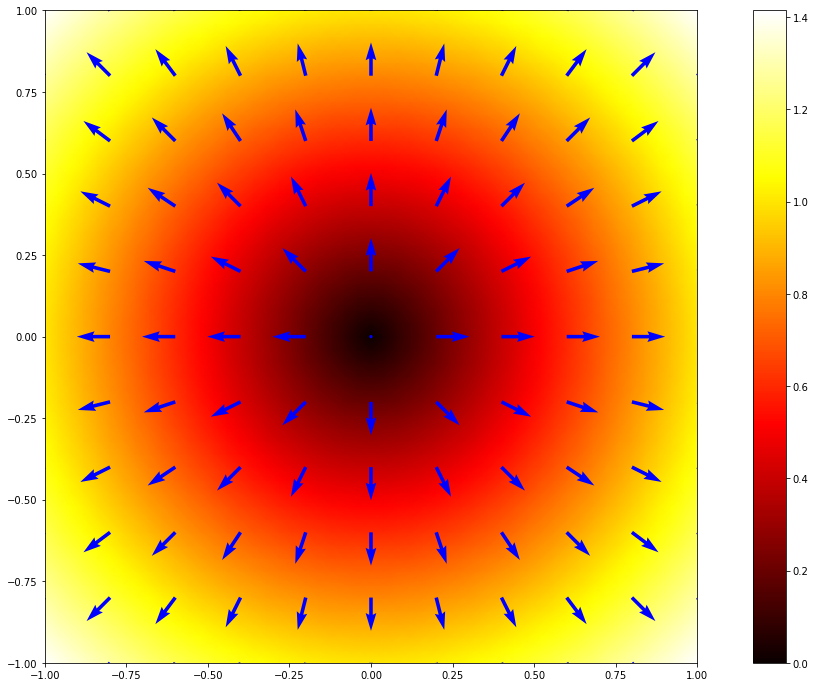
Tok v izotropním materiálu (keramika, kov)¶
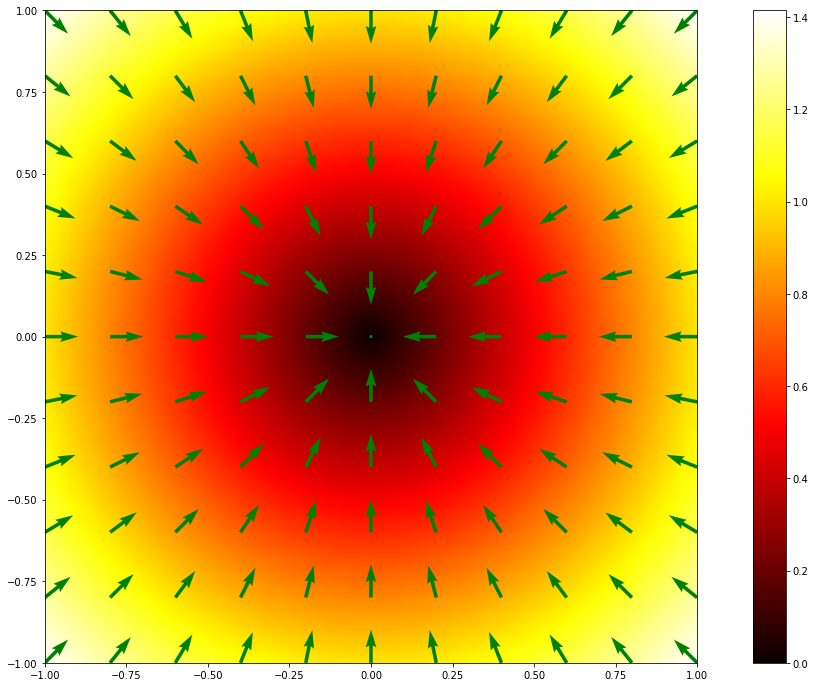
Nerovnoměrnost v rozložení teploty popsaná v předchozím odstavci bude tvořit hnací faktor snažící se hnát teplo opačným směrem, než jakým narůstá teplota. Bude to opravdu směr toku? Pokud bude materiál izotropní (bude mít ve všech směrech stejné vlastnosti), jako například kov nebo keramika, je odpověď na tuto otázku kladná. Teplo bude mít tendenci téct na opačnou stranu než je směr gradientu. Jak intenzivní tok tepla bude závisí na materiálu. Jinak to dopadne pro měď a jinak pro keramiku. Může to dopadnout například následovně. Všimněte si, že všechny šipky míří do středu, tedy přesně ve směru klesající teploty. A přesně proti směru gradientu.
tokx = -gradx
toky = -grady
fig, ax = plt.subplots(1,1, figsize=(20,12)) # inicializace grafiky
output = plt.pcolormesh(x, y, z, cmap=cmap, shading='gouraud') # vykresleni barevne mapy pomocí zvolené barevné mapy a vyhlazování přechodů
plt.colorbar(output) # barevný sloupec s hodnotami vedle grafu
plt.quiver(x[::ps,::ps], y[::ps,::ps], tokx[::ps,::ps], toky[::ps,::ps], color='green')
# vykreslení toku, na řidší mřížce než termosnímek
ax.set_aspect(1)
None
Tok v ortotropním materiálu (dřevo)¶
V ortotorpních a izotrpních materiálech závisí materiálové vlastnosti na směru. Typicky se jedná o materiály, které mají jistou strukturu. Nejhezčím a nejdostupnějším takovým materiálem je dřevo.
Naopak, materiály, které takovou strukturu nemají a jejich stavební části jsou uspořádány chaoticky, bývají izotropní. Například kov nebo guma. I v tomto případě však je možné strukturu dodat, čímž se změní vlastnosti materiálu a materiál přestane být izotropní a začne vykazovat v odlišných směrech odlišné vlasnosti. Například kov válcovaný za studena nebo napnutá guma.
V takových případech je závislost toku $\vec q$ na gradientu $\nabla u$ stavové veličiny $u$ popsána obecnou funkční závislostí $$ \vec q= \vec F (\nabla u),$$ přičemž nulový vektor se zobrazuje na nulový vektor, protože bez podnětu není odezva, tedy $$ \vec F(0)=0,$$ kde nula v tomto případě označuje nulový vektor.
Lineární aproximace¶
Připomeňme, jak funguje lineární aproximace pro vektorové funkce. Vyjdeme z aproximace obecné vektorové funkce $\vec F$ se dvěma komponentami $f_1(x,y)$ a $f_2(x,y)$. V okolí bodu $(x_0,y_0)$ jsou komponenty této funkce aproximovány vztahy $$ f_1(x,y)\approx f_1(x_0, y_0)+\frac{\partial f_1 (x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial f_1 (x_0,y_0)}{\partial y}(y-y_0)$$ a $$ f_2(x,y)\approx f_2(x_0, y_0)+\frac{\partial f_2 (x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial f_2 (x_0,y_0)}{\partial y}(y-y_0).$$ Pro nulovou odezvu při nulovém podnětu máme $x_0=y_0=f_1(0,0)=f_2(0,0)=0,$ čímž dostáváme $$ f_1(x,y)\approx \frac{\partial f_1 (0,0)}{\partial x}x+\frac{\partial f_1 (0,0)}{\partial y}y$$ a $$ f_2(x,y)\approx \frac{\partial f_2 (0,0)}{\partial x}x+\frac{\partial f_2 (0,0)}{\partial y}y.$$ Použitím maticového součinu a Jacobiho matice $$J(x,y)=\begin{pmatrix} \frac{\partial f_1}{\partial x}(x ,y ) & \frac{\partial f_1}{\partial y}(x ,y )\cr \frac{\partial f_2}{\partial x}(x ,y ) & \frac{\partial f_2}{\partial y}(x ,y )\end{pmatrix}$$ můžeme tento vztah zapsat jako $$ \vec F (x,y) \approx J(0,0) \begin{pmatrix} x\cr y\end{pmatrix}.$$ Pokud toto vyjádření použijeme pro gradient, dostáváme $$ \vec F(\nabla u)\approx - D \nabla u,$$ kde $D=-J(0,0)$ je záporně vzatá Jacobiho matice.
Tenzorová formulace konstitutivního zákona¶
Jacobiho matice z předešlého navíc splňuje jisté vztahy, které vyjadřují to, že fyzikální realita je nezávislá na zvolené souřadné soustavě, ve které problém studujeme. Matice, které mají ještě další vlastnosti vyplývající z chování při transformacích, nazývají tenzory. Pomocí nich můžeme konstituvní zákon zapsat ve tvaru $$ \vec q = -D\nabla u,$$ kde $D$ je matice a $u$ stavová veličina. Podle kontextu mají uvedený vztah a matice $D$ speciální název.
Například při studiu vedení tepla jde o Fourierův zákon a součinitel tepelné vodivosti.
V případě pohybu vody ve dřevě nebo obecně v případě difuze jde o Fickův zákon a difuzní koeficient.
V případě pohybu podzemní vody mluvíme o Darcyho zákoně a transmisivitě.
Vlastní směry materiálu¶
U vhodně natočených souřadných os je matice $D$ diagonální. To znamená, že pokud vektor gradientu je směru osy $x$, tok je opět ve směru osy $x$. Skutečně, vektory ve směru osy $x$ mají druhou komponentu nulovou a z maticového součinu plyne $$ \begin{pmatrix} D_x & 0 \cr 0 & D_y \end{pmatrix} \begin{pmatrix} \frac{\partial u}{\partial x} \cr 0 \end{pmatrix} = \begin{pmatrix} D_x\frac{\partial u}{\partial x} \cr 0 \end{pmatrix} = D_x\begin{pmatrix} \frac{\partial u}{\partial x} \cr 0 \end{pmatrix}.$$ Podobně pro gradient a tok ve směru osy $y$ máme $$ \begin{pmatrix} D_x & 0 \cr 0 & D_y \end{pmatrix} \begin{pmatrix} 0\cr \frac {\partial u}{\partial y} \end{pmatrix} =\begin{pmatrix} 0\cr D_y\frac{\partial u}{\partial y} \end{pmatrix} = D_y \begin{pmatrix} 0\cr \frac{\partial u}{\partial y} \end{pmatrix}. $$ To znamená, že v těchto směrech je tok proti směru gradientu. V těchto směrech je reakce materiálu určitým způsobem snadněji popsatelná, než v obecném případě, kdy máme $$ \begin{pmatrix} D_x & 0 \cr 0 & D_y \end{pmatrix} \begin{pmatrix} \frac{\partial u}{\partial x}\cr \frac{\partial u}{\partial y} \end{pmatrix} = \begin{pmatrix} D_x \frac{\partial u}{\partial x} \cr D_y\frac{\partial u}{\partial y} \end{pmatrix} $$ a výsledný tok $\begin{pmatrix} D_x \frac{\partial u}{\partial x} \cr D_y\frac{\partial u}{\partial y} \end{pmatrix}$ má obecně jiný směr než podnět $\begin{pmatrix} \frac{\partial u}{\partial x} \cr \frac{\partial u}{\partial y} \end{pmatrix}.$ Jak vlastní směry nalézt necháme teď bokem, jenom stručně zmíníme možnosti. U dřeva se stačí podívat na strukturu. U obecnějšího materiálu můžeme vlastní směry identifikovat experimentem. U materiálu u kterého známe difuzní matici i s příslušnou nenulovou mimodiagonální složkou můžeme vlastní směry vypočítat, zvolit novou souřadnou soustavu v těchto vlastních směrech a difuzní matice v této nové soustavě bude diagonální.
Numerický experiment¶
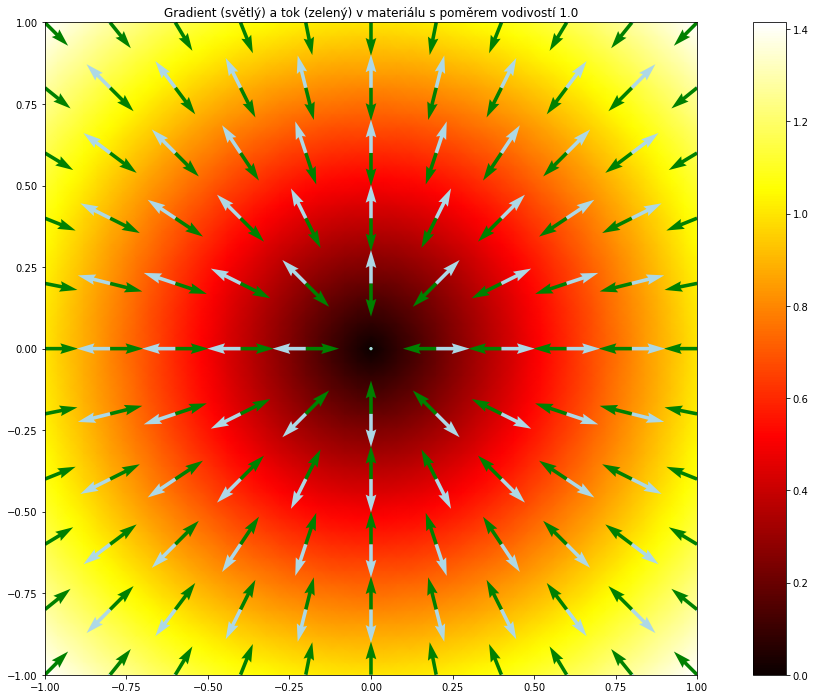
Zkusíme namodelovat vliv různých difuzních koeficientů v diagonální matici na tok. Budeme modelovat tok v materiálech popsaných difuzní rovnicí, kde matice je nejprve jednotková a koeficient $D_y$ se postupně zvyšuje na pětinásobek původní hodnoty. Co sledovat?
Pokud je $D_x=D_y=1$ (první obrázek), jedná se o izotropní materiál. Tok je ve směru klesající stavové veličiny, tj. přesně proti gradientu. Šipky znázorňující tok a gradient míří přesně opačným směrem.
Na dalších obrázcích postupně narůstá tendence materiálu stáčet tok do svislého směru, protože roste $D_y$. Gradient zůstává, ale tok se stáčí do svislého směru.
Pokud míří gradient vodorovně nebo svisle, tok je proti směru gradientu i v případě odlišných $D_x$ a $D_y$. To je v souladu se závěry předchozího odstavce. Některé směry tedy mají tu vlastnost, že tok je ve směru podnětu. U materiálu s pravidelnou strukturou to jsou směry vyplývající ze této struktury. Například u dřevěné desky uvažované jako 2D materiál by se jednalo o podélný směr a směr k němu kolmý. V ostatních směrech se tok odkldání od směru maximálního poklesu ve prospěch podélného směru dřeva.
V důsledku uvedeného máme následující pozorování.
Na prvním obrázku jsou šipky znázorňující gradient a tok přesně naopak. Dále to tak není.
Ve všech obrázcích míří šipky znázorňující tok a gradient proti sobě v případě, že tento směr je vodorovný nebo svislý. Sledujte vodorovné a svislé řezy středem čtverce (počátkem). Na všech obrázcích to vypadá podobně.
S výjimkou prvního obrázku je směr šikmých šipek znázorňujících gradient jiný, než směr toku v daném bodě. Tendence odklánět to do svislého směru je tím vyšší, čím je větší nepoměr mezi $D_x$ a $D_y$. Sledujte rohy čtverců. Situace na obrázcích se dramaticky mění. Zelená šipka (tok) se stále více stáčí do svislého směru.
Dx = 1
for Dy in numpy.linspace(1,5,5):
D = numpy.array([[Dx,0],[0,Dy]])
tokx,toky = -D[0,0]*gradx - D[0,1]*grady, -D[1,0]*gradx - D[1,1]*grady,
fig, ax = plt.subplots(1,1,figsize=(20,12)) # inicializace grafiky
plt.quiver(x, y, gradx, grady, color='blue')
output = plt.pcolormesh(x, y, z, cmap=cmap, shading='gouraud') # vykresleni barevne mapy pomocí zvolené barevné mapy a vyhlazování přechodů
fig.colorbar(output) # barevný sloupec s hodnotami vedle grafu
plt.quiver(x[::ps,::ps], y[::ps,::ps], tokx[::ps,::ps], toky[::ps,::ps], color='green') # vykreslení toku
plt.quiver(x[::ps,::ps], y[::ps,::ps], gradx[::ps,::ps], grady[::ps,::ps], color='lightblue') # vykreslení gradientu
plt.title("Gradient (světlý) a tok (zelený) v materiálu s poměrem vodivostí %s"%str(Dy))
ax.set_aspect(1)
None
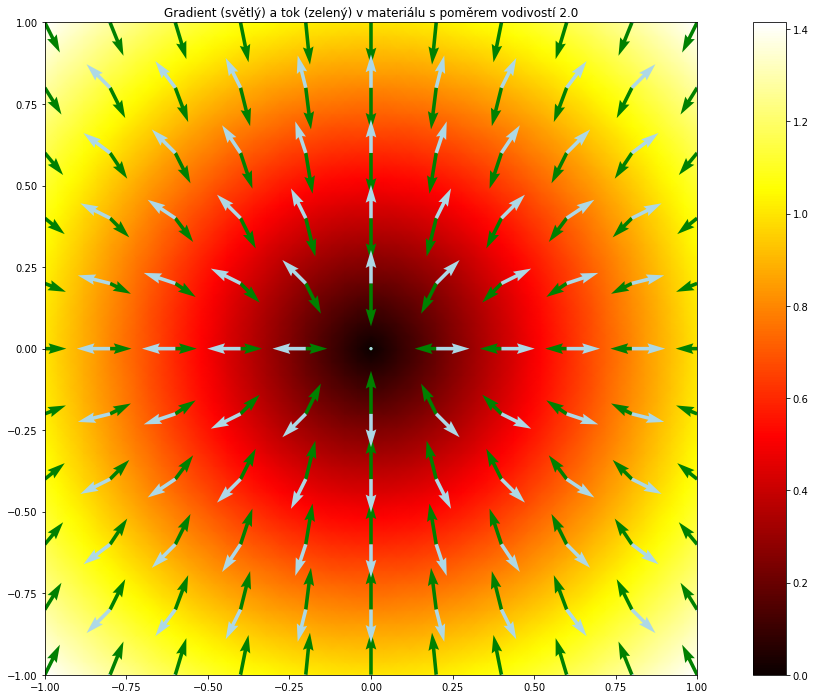
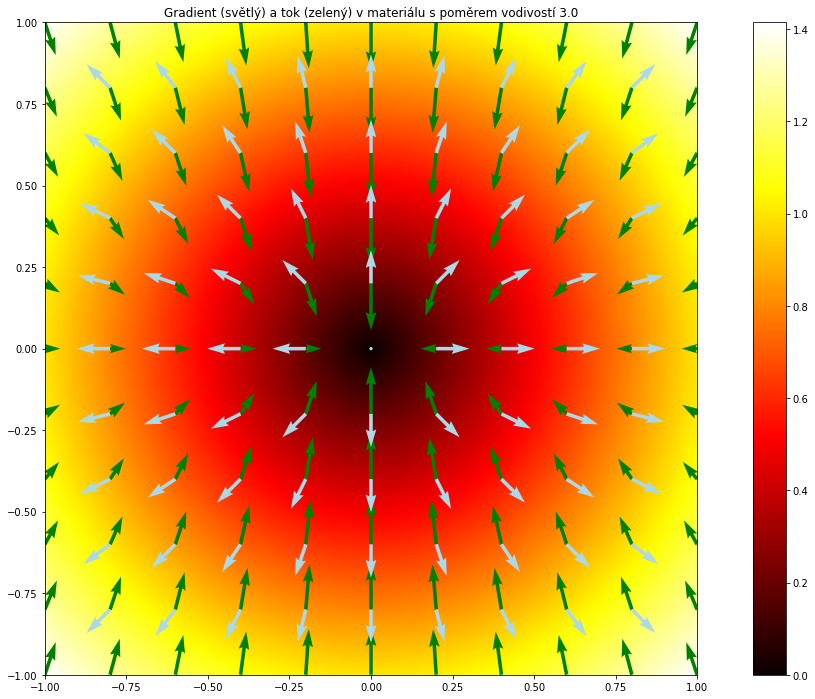
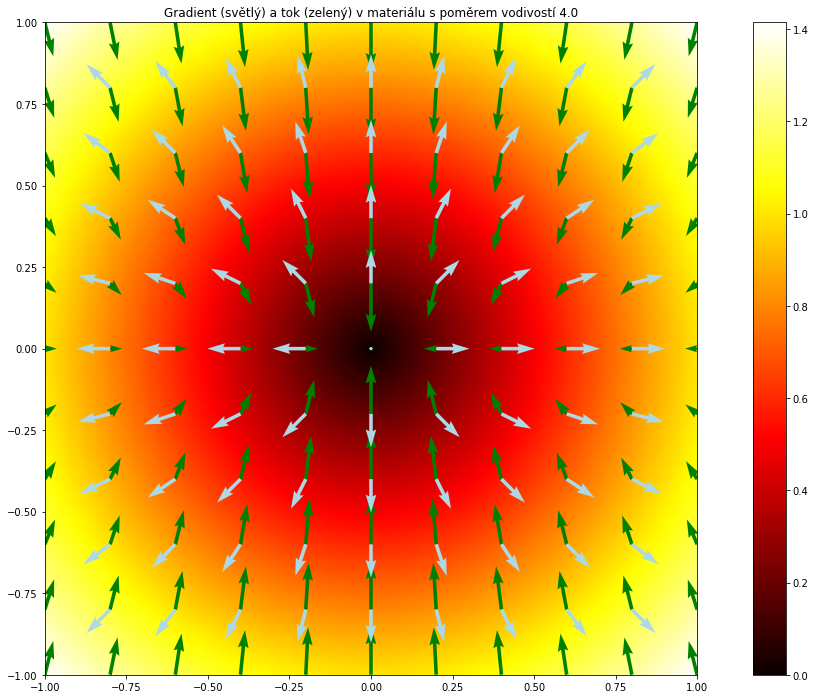
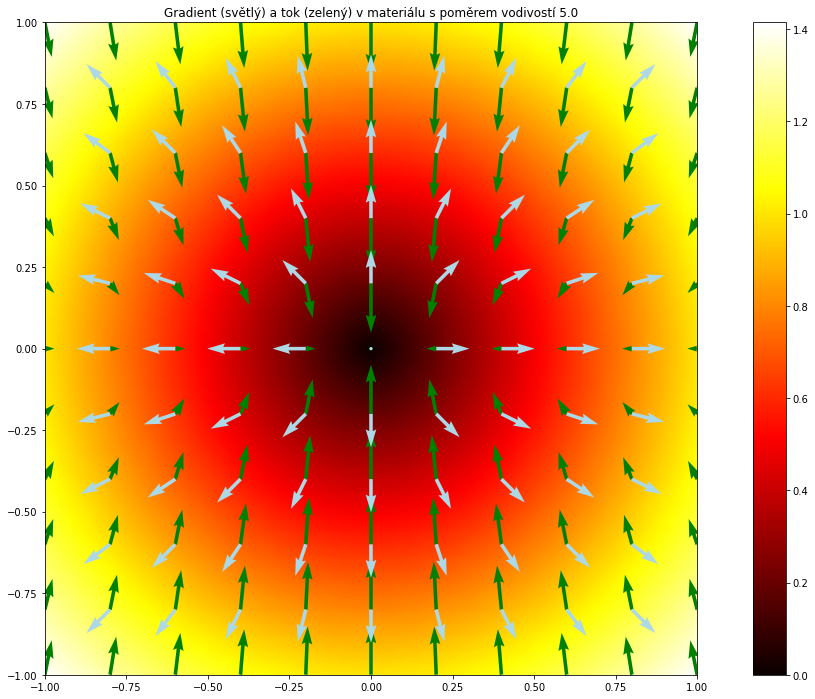
A na závěr ještě jedno pozorování: u ortotropních materiálů s podnětem ve vlastním směru je odezva ve stejném směru jako podnět, což vidíme na obrázcích na ose $x$ a $y$. Na obou osách je světlá šipka přímo proti zelené. Přesto situace není stejná. Čím více se mění nepoměr mezi difuzními koeficienty v jednotlivých směrech, tím více je patrné, že sice na obou osách směr toku koresponduje se záporně vzatým gradientem, ale situace týkající se intenzity toku (délky šipky) je odlišná. Na obou osách jsou bílé šipky stejně dlouhé, tj. gradient je stejný. Zelené šipky na ose $y$ však jsou mnohem delší než šipky na ose $x$ a tento nepoměr je tím větší, čím je větší nepoměr mezi difuzními koeficienty v jednotlivých směrech.
