Nezávislost na integrační cestě¶
V učebnicích často najdete příklady na výpočet křivkového integrálu pomocí potenciálu, protože toto je jednodušší v ručně vypočítatelných příkladech. Pro numerickou integraci je často situace přesně opačná. Křivkový integrál je relativně snadné vypočítat robustními metodami a jeho výpočet vede k jedné z cest, jak potenciál určit.
Zkusíme si problematiku ilustrovat na příkladu dvou vektorových polí a dvou integračních cest v každém z nich.
První pole bude nevírové, bude v něm existovat skalární potenciál a integrace po obou cestách (zvolíme přímku a kubickou parabolu) dá stejný výsledek. Kterákoliv z těchto “cest” vede ke stejné skalární funkci, která ekvivalentním způsobem charakterizuje vektorové pole a je skalárním potenciálem tohoto pole.
Druhé vektorové pole bude vírové, nebude v něm existovat skalární potenciál a poznáme to podle toho, že pokud se budeme snažit jej hledat, tak skalární funkce, která by mohla jeho roli hrát, bude vycházet jinak pro přímky a jinak pro kubické funkce.
Vektorové pole se skalárním potenciálem¶
Budeme si demonstrovat závislost či nezávislost na integrační cestě. Budeme pro zadané vektorové pole $$\vec F=(6x^2y+x+y)\vec i + (2x^3+x)\vec j$$ počítat křivkový integrál po dvou různých křivkách, po přímce a po kubické parabole. Křivky budou vycháztet z počátku a koncový bod bude parametrizován, abychom jím mohli pohybovat v rovině. Budeme tak moci vypočítat křivkový integrál z počátku do libovolného bodu roviny.
Ve cvičení bylo ukázáno, že k tomuto vektorovému poli existuje kmenová funkce $$ \varphi (x,y)=2x^3y+\frac 12 x^2+xy+C.$$ Nyní si tento proces vyzkoušíme numericky. Protože budeme integrovat z počátku, očekáváme, že výsledkem bude potenciál, který je v počátku roven nule, tj. funkce $$ \varphi (x,y)=2x^3y+\frac 12 x^2+xy.$$
import numpy # knihovna na numerické výpočty (goniomerické funkce, gradient, 2D mřížka a dělení intervalu, ...)
import scipy.integrate # knihovna na technické výpočty (integrál)
import matplotlib.pyplot as plt # knihovna na kreslení
x = numpy.linspace (0,4,21) # diskretizace intervalu pro x
y = numpy.linspace (0,4,21) # diskretizace intervalu pro y
Y, X = numpy.meshgrid(x, y) # mřížka v rovině z bodů, do kterých budeme počítat křivkový integrál
PotencialPrimka = numpy.zeros((x.shape[0],y.shape[0])) # naplnění pole pro výsledky integrace po přímkách nulami
PotencialParabola = numpy.zeros((x.shape[0],y.shape[0])) # naplnění pole pro výsledky integrace po kubických parabolách nulami
Zkusíme dvě integrační cesty z bodu $(0,0)$ do bodu $(x,y)$. Přímku $$\vec r(t)=xt\vec i + yt\vec j, \quad t\in[0,1] $$ a kubickou parabolu $$\vec r(t)=xt\vec i + yt^3\vec j, \quad t\in[0,1].$$ Křivkové integrály přetransformujeme na Riemannovy $$\int_0^1 P(xt,yt)x+Q(xt,yt)y, \mathrm dt $$ pro integrál po přímce a $$\int_0^1 P(xt,yt^3)x+Q(xt,yt^3)y3t^2, \mathrm dt $$ pro integrál po parabole a numerickou integrací tyto integrály vypočteme.
def KrivkovyIntegralPrimka(P, Q, a,b): # Definice procedury pro vypocet integralu po přímce
t = numpy.linspace(0,1,100) # Nastavíme interval pro diskretizaci integrálu
integrand = P(a*t,b*t)*a+Q(a*t,b*t)*b # Vypočteme skalární součin vektorového pole a tečného vektoru k přímce
return(scipy.integrate.simps(integrand,t)) # Vypočteme integrál a vrátíme jako výstup funkce
def KrivkovyIntegralParabola(P, Q, a,b): # Definice procedury pro vypocet integralu po přímce
t = numpy.linspace(0,1,100) # Nastavíme interval pro diskretizaci integrálu
integrand = P(a*t,b*t**3)*a+Q(a*t,b*t**3)*3*b*t**2 # Vypočteme skalární součin vektorového pole a tečného vektoru ke kubické parabole
return(scipy.integrate.simps(integrand,t)) # Vypočteme integrál a vrátíme jako výstup funkce
Nadefinujeme komponenty vektorového pole a vypočteme křivkové inetrgály do jednotlivých bodů v rovině. Ve dvojitém cyklu tedy nakonec počítáme obrovské množství intergrálů, ale ani tak to moc dlouho netrvá.
def P(x,y): # definice komponent vektorového pole
return (6*x**2*y+x+y)
def Q(x,y):
return (2*x**3+x)
for i in range(x.shape[0]): # Vyplníme pole s hodnotami potenciálu příslušnými hodnotami v cyklu přes první a druhou proměnnou
for j in range(y.shape[0]):
PotencialPrimka[i][j] = KrivkovyIntegralPrimka(P, Q, x[i], y[j]) # Výpočet a uložení integálu po přímce
PotencialParabola[i][j] = KrivkovyIntegralParabola(P, Q, x[i], y[j]) # Výpočet a uložení integálu po kubické parabole
fig, axes = plt.subplots(1,2, figsize=(20,8)) # inicializace grafiky
ax = axes[0] # začneme kreslit do prvního grafu
cmap = plt.get_cmap('hot') # nastaveni schema pro barevnou mapu
output = ax.pcolormesh(X, Y, PotencialPrimka, cmap=cmap, shading='gouraud') # vykresleni barevne mapy pomocí zvolené barevné mapy a vyhlazování přechodů
plt.colorbar(output, ax=ax, label="Potenciál") # barevný sloupec s hodnotami vedle grafu
ax.set_aspect(1) # stejné měřítko na osách, aby se kružnice nedeformovaly
ax.set_title("Výsledky integrálů po přímkách") # nadpis grafu
ax = axes[1] # začneme kreslit do prvního grafu
output = ax.pcolormesh(X, Y, PotencialParabola, cmap=cmap, shading='gouraud') # vykresleni barevne mapy pomocí zvolené barevné mapy a vyhlazování přechodů
plt.colorbar(output, ax=ax, label="Potenciál") # barevný sloupec s hodnotami vedle grafu
ax.set_aspect(1) # stejné měřítko na osách, aby se kružnice nedeformovaly
ax.set_title("Výsledky integrálů po parabolách") # nadpis grafu
None
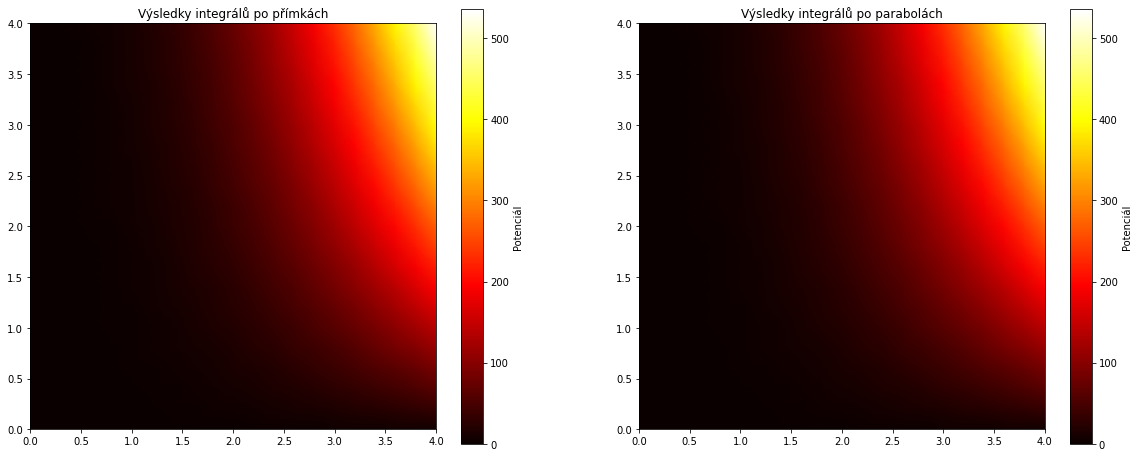
Vidíme, že obrázky vypadají přibližně stejně. To je dobré znamení, ale přesvědčivější bude zjistit, o kolik se výsledky liší numericky. Najdeme maximum a průměr absolutní hodnoty rozdílu. Po výpočtu vidíme, že ve srovnání s funkčními hodnotami je tento rozdíl zanedbatelný. Je připsatelný na vrub tomu, že neintegrujeme symbolicky a přesně, ale numericky na mřížce s konečně velkým krokem.
numpy.amax(abs(PotencialPrimka-PotencialParabola)) # Maximum absolutní hodnoty rozdílu
0.0020979988173621678
numpy.average(abs(PotencialPrimka-PotencialParabola)) # Průměr absolutní hodnoty rozdílu
0.0002773205040675051
Vektorové pole bez skalárního potenciálu¶
Pokusíme se provést totéž co výše pro vektorové pole $$ \vec F=x\vec i+(y-x^2)\vec j,$$ tj. komponenty vektorového pole budou $$ P(x,y)=x $$ a $$ Q(x,y)=y-x^2.$$ Najdeme křivkové integrály z počátku do bodu $(x,y)$ a znázorníme výsledné hodnoty graficky v rovině. Použijeme dvě různé integrační cesty. To povede ke dvěma různým výsledkům, protože $$ \begin{aligned}\frac{\partial P}{\partial y}&=0\cr \frac{\partial Q}{\partial x}&=-2x\end{aligned}$$ a obě parciální derivace jsou různé. To znamená, že vektorová funkce nemá potenciál a v takovém případě snaha integrovat po různých cestách vede k různým výsledkům. Obrázky jsou zřetelně odlišné.
def P(x,y): # definice komponent nového vektorového pole
return (x)
def Q(x,y):
return (y-x**2)
PotencialPrimka = numpy.zeros((x.shape[0],y.shape[0])) # vynulování polí pro uložení výsledků
PotencialParabola = numpy.zeros((x.shape[0],y.shape[0]))
for i in range(x.shape[0]): # integrace do jednotlivých bodů mřížky ve dvojitém cyklu přes všechny body této mřížky
for j in range(y.shape[0]):
PotencialPrimka[i][j] = KrivkovyIntegralPrimka(P, Q, x[i], y[j]) # výpočet integrálu po přímce
PotencialParabola[i][j] = KrivkovyIntegralParabola(P, Q, x[i],y[j]) # výpočet integrálu po kubické parabole
fig, axes = plt.subplots(1,2, figsize=(20,8)) # inicializace grafiky
Zmin = numpy.amin([PotencialPrimka, PotencialParabola]) # Určíme minimum a maximumu pro stavení barevné škály
Zmax = numpy.amax([PotencialPrimka, PotencialParabola]) #
ax = axes[0] # začneme kreslit do prvního grafu
output = ax.pcolormesh(X, Y, PotencialPrimka, cmap=cmap, shading='gouraud', vmin=Zmin, vmax=Zmax) # vykresleni barevne mapy pomocí zvolené barevné mapy a vyhlazování přechodů
plt.colorbar(output, ax=ax, label="Potenciál") # barevný sloupec s hodnotami vedle grafu
ax.set_aspect(1) # stejné měřítko na osách, aby se kružnice nedeformovaly
ax.set_title("Výsledky integrálů po přímkách")
ax = axes[1] # začneme kreslit do prvního grafu
output = ax.pcolormesh(X, Y, PotencialParabola, cmap=cmap, shading='gouraud', vmin=Zmin, vmax=Zmax) # vykresleni barevne mapy pomocí zvolené barevné mapy a vyhlazování přechodů
plt.colorbar(output, ax=ax, label="Potenciál") # barevný sloupec s hodnotami vedle grafu
ax.set_aspect(1) # stejné měřítko na osách, aby se kružnice nedeformovaly
ax.set_title("Výsledky integrálů po parabolách")
None
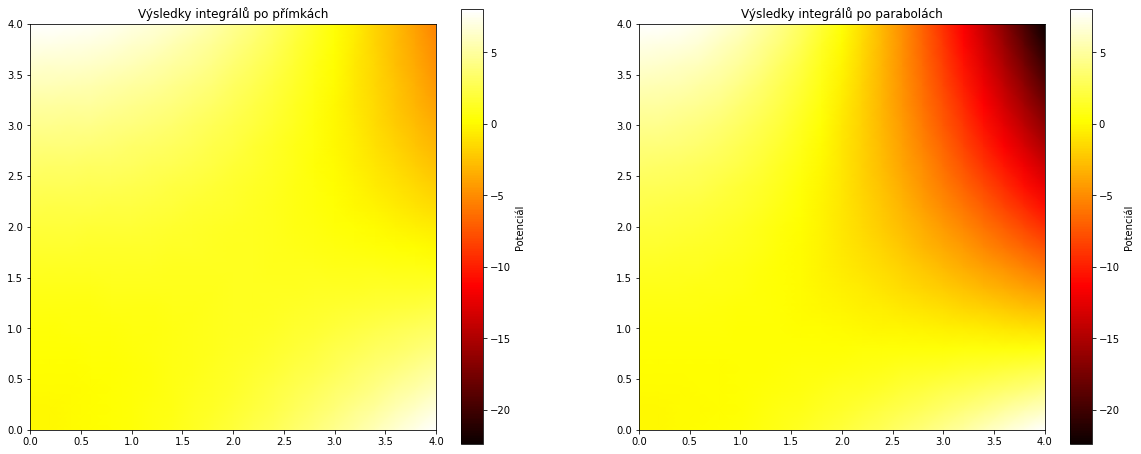
Grafická kontrola je dostatečně průkazná, v pravém horním rohu je situace silně odlišná. Můžeme vypočítat i maximum rozdílu mezi funkčními hodnotami. Je srovnatelné s funkčními hodnotami, tedy nemůže být připsáno na vrub diskretizaci.
numpy.amax(abs(PotencialPrimka-PotencialParabola)) # maximální hodnota, o kterou se liší výpočet integrálů po různých cestách
17.066713114092696
numpy.average(abs(PotencialPrimka-PotencialParabola)) # průměrná hodnota, o kterou se liší výpočet integrálů po různých cestách
2.9155578523049726
Potenciálové versus nepotenciálové pole¶
Proč vlastně chceme vědět, zda je možné ve vektrorovém zavést skalární potenciál? Existence skalárního potenciálu umožní přejít k alternativnímu popisu pole. V naprosté většině případů se to vyplatí, protože se skalárními funkcemi se pracuje lépe než s funkcemi vektorovými.
Jako robustnější kriterium než porovnávat obrázky je možné například testovat integrály po uzavřených křivkách. Pokud vychází nulové, je vektorové pole potenciálové. Pokud integrály po uzavřených křivkách vychází výrazně nenulové (tak, že případná nenulovost nemůže být způsobena jenom zaokrouhlováním při diskretizaci spojité veličiny), je to signál toho, že skalární popis pomocí potenciálu není možno zavést.
Další varianta testu na možnost zavedení potenciálu je výpočet rotace derivováním. To si ukážeme v následující. Protože máme dvourozměrné pole, má rotace první dvě komponenty nulové a zkráceně rotací budeme nazývat jenom třetí komponentu vektoru rotace. Rotaci vypočteme vzorcem $$\nabla \times (P,Q,0)=\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\vec k.$$ Derivace vystupující v této rotaci budeme počítat pomocí centrálních diferencí podle vzorců $$\frac{\partial Q}{\partial x}\approx \frac{Q(x+h,y)-Q(x-h,y)}{2h}$$ a $$\frac{\partial P}{\partial y}\approx \frac{P(x,y+h)-P(x,y-h)}{2h}.$$ Délku kroku odvodíme z disketizace prostoru.
def rotace(P,Q,x,y): # nadefinujeme funkci pro výpoče rotace
krokx=(x[-1]-x[0])/(x.shape[0]-1) # vzdálenost mezi sousedními uzly na dělení pro x se použije jako ...
kroky=(y[-1]-y[0])/(y.shape[0]-1) # ... diferenční krok při derivaci podle x, podobně pro y
vysledek=numpy.zeros((x.shape[0],y.shape[0])) # příprava pole pro uložení výpočtů
for i in range(1,x.shape[0]-1): # dvojitý cyklus pro výpočet hodnot na dvourozměnré mřížce
for j in range(1,y.shape[0]-1):
dQ_podle_x=(Q(x[i+1],y[j])-Q(x[i-1],y[j]))/(2*krokx) # derivace Q podle x
dP_podle_y=(P(x[i],y[j+1])-P(x[i],y[j-1]))/(2*kroky) # derivace P podle y
vysledek[i][j]= dQ_podle_x - dP_podle_y # rotace vektoroveho pole (P,Q)
return(vysledek) # výstup výpočtu rotace
# Abychom nemuseli znovu pojmenovávat funkce, jejichž rotaci počítáme, použijeme trik s nepojmenovanou ...
# ... funkcí pomocí konstrukce lambda x,y:funkční hodnota
R1=rotace(lambda x,y:6*x**2*y+x+y,lambda x,y:2*x**3+x,x,y) # výpočet rotace vektorového pole (6*x^2+x+y, 2*x^3+x)
R2=rotace(lambda x,y:x,lambda x,y:y-x**2,x,y) # výpočet rotace vektorového pole (x, y-x^2)
Po výpočtu je možno například najít maximální absolutní hodnotu, nebo součet absolutních hodnot či jejich druhých mocnin, nebo vykreslit vypočtené hodnoty graficky. Zvolíme poslední možnost, použijeme stejné příkazy jako u vizualizce výsledku křivkového integrálu po různých cestách výše. Jenom musíme vzít v úvahu, že pro porovnání obrázků je nutné najít společné maximum a minium zobrazovaných funkcí a podle toho nastavit barevnou škálu.
fig, axes = plt.subplots(1,2, figsize=(20,8)) # inicializace grafiky
Zmin = numpy.amin([R1, R2]) # Určíme minimum a maximumu pro stavení barevné škály
Zmax = numpy.amax([R1, R2]) #
ax = axes[0] # začneme kreslit do prvního grafu
output = ax.pcolormesh(X, Y, R1, cmap=cmap, shading='gouraud', vmin=Zmin, vmax=Zmax) # vykresleni barevne mapy pomocí zvolené barevné mapy a vyhlazování přechodů
plt.colorbar(output, ax=ax, label="Rotace") # barevný sloupec s hodnotami vedle grafu
ax.set_aspect(1) # stejné měřítko na osách, aby se kružnice nedeformovaly
ax.set_title("Rotace vektorového pole majícího potenciál")
ax = axes[1] # začneme kreslit do prvního grafu
output = ax.pcolormesh(X, Y, R2, cmap=cmap, shading='gouraud', vmin=Zmin, vmax=Zmax) # vykresleni barevne mapy pomocí zvolené barevné mapy a vyhlazování přechodů
plt.colorbar(output, ax=ax, label="Rotace") # barevný sloupec s hodnotami vedle grafu
ax.set_aspect(1) # stejné měřítko na osách, aby se kružnice nedeformovaly
ax.set_title("Rotace vektorového pole ve kterém neexistuje potenciál")
None
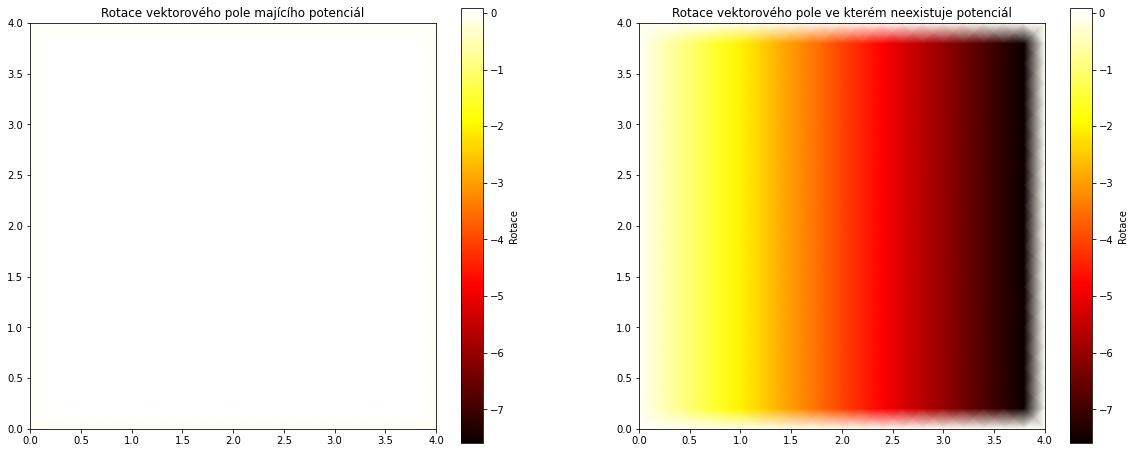
Závěr¶
Hledali jsme pomocí křivkového integrálu skalární potenciál vektorového pole. Jednou z toho v případě předem odsouzeném pro nezdar, kdy skalární potenciál neexistuje. Zvolili jsme pro jednoduchost grafické porovnání, protože zřetelně ilustruje rozdíl. Výsledek jsme potvrdili výpočtem rotace. U vektorového pole se skalárním potanciálem je rotace nulová, u druhého nenulová.
