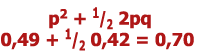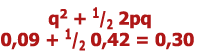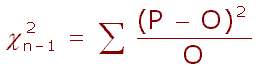Genetická rovnováha

Hardyho - Weinbergův zákon

Jestliže se velká diploidní populace pohlavně panmikticky rozmnožuje, nemění se její genetická struktura, protože její alelové a genotypové četnosti jsou konstantní z generace na generaci. Pak se hovoří, že populace je v genetické (genotypové) rovnováze.

Princip genetické rovnováhy odhalili nezávisle na sobě v roce 1908 anglický matematik G.H. Hardy a německý lékař W. Weinberg. Hardyho-Weinbergův zákon (princip rovnováhy) je jeden ze základních koncepcí genetiky populací kvalitativních znaků. Předpovídá, jak budou přenášeny frekvence alel z generace na generaci za specifických podmínek. Zákon rovnováhy má tři hlavní vlastnosti:

  1. frekvence alel předpovídají (určují) frekvence genotypů,
  2. v rovnováze se frekvence alel a genotypů nemění z generace na generaci,
  3. rovnováha je dosažena za jednu generaci náhodného páření.
Podmínky H.-W. rovnováhy

  1. Populace je nekonečně velká, což v praxi znamená, že populace je dost velká na to, aby náhodné chyby výběru a další náhodné efekty byly zanedbatelné.

  2. Organizmy jsou diploidní.

  3. Páření v populaci se děje náhodně (panmixie).

  4. Generace se nepřekrývají.

  5. Nepůsobí selekce proti žádnému genotypu, tzn. všechny rozmnožované genotypy jsou stejně životaschopné a plodné (všichni jedinci mají stejnou plodnost).

  6. Nepůsobí další faktory včetně mutace, migrace a náhodného driftu (evoluční síly).

Základní model je mnohybrid s alelami A a a. Mendelistickou segregaci můžeme vyjádřit binomickým rozvojem: (a+b)n = (A+a)2 = 1 AA + 2 Aa + 1aa. Zobecňuje se frekvence f(A) ~ p, f(a) ~ q.

 Gamety vybrané z genofondu populace tvoří genotypy příští generace. V tomto případě samci a samice mají stejné frekvence (p) dominantní alely A a stejné frekvence (q) recesivní alely a. Po páření mají tři genotypy AA, Aa a aa frekvence p2, 2pq a q2.

Distribuci genotypů v příští generaci za genetické rovnováhy lze zapsat:
 
Pokud je populace v genetické rovnováze, mohou být frekvence alel a genotypů vypočítány pouze ze známé frekvence jednoho genotypu (zpravidla recesivního homozygota).
 

V této populaci je frekvence dominantní alely f(A) = p = 0,7 a frekvence recesivní alely f(a) = q = 0,3. použitím rovnice genetické rovnováhy jsou frekvence genotypů v příští generaci AA = 0,49, Aa = 0,42 a aa = 0,09. 

Frekvence alel zůstávají konstantní z generace na generaci:

 

Jedna frekvence alel může v různých populacích mít různé frekvence genotypů. Ale jen jedna populace je v genetické rovnováze, neboť její frekvence genotypové odpovídají frekvencím rovnice genetické rovnováhy p2 + 2pq + q2 = 1. Z četnosti alel nelze vypočítat četnosti genotypů, protože jedné četnosti alel mohou odpovídat různé četnosti genotypů.

p (A) q (a) p2 (AA) 2pq (Aa) q2 (aa)
0,80 0,20 0,60 0,40 0,00
0,80 0,20 0,61 0,38 0,01
0,80 0,20 0,64 0,32 0,04
0,80 0,20 0,70 0,20 0,10
0,80 0,20 0,75 0,10 0,15
0,80 0,20 0,80 0,00 0,20

Rovnovážný stav pro různé frekvence alel. Všimněte si, že čím nižší četnost alely, tím větší je její výskyt v heterozygotech:

p (A) q (a) p2 (AA) 2pq (Aa) p2 (aa) p2 + 2pq 2pq:q2
0,99 0,01 0,9801 0,0198 0,0001 0,9999 198:1
0,95 0,05 0,9025 0,0950 0,0025 0,9975 38:1
0,90 0,10 0,81 0,18 0,01 0,99 18:1
0,80 0,20 0,64 0,32 0,04 0,96 8:1
0,70 0,30 0,49 0,42 0,09 0,91 4,7:1
0,60 0,40 0,36 0,48 0,16 0,84 3:1
0,50 0,50 0,25 0,50 0,25 0,75 2:1
0,40 0,60 0,16 0,48 0,36 0,64 1,3:1
0,30 0,70 0,09 0,42 0,49 0,51 0,86:1
0,20 0,80 0,04 0,32 0,64 0,36 0,5:1
0,10 0,90 0,01 0,18 0,81 0,19 0,22:1

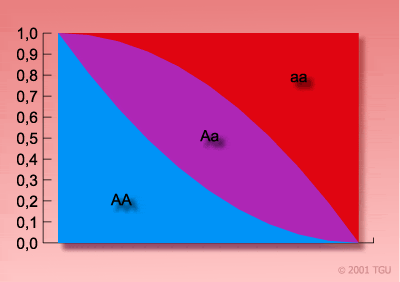
Grafické zobrazení genetické rovnováhy - vztah mezi frekvencemi genotypů a alel odvozený z H.-W. rovnováhy.

Odvoďte vztah mezi genetickou rovnováhou a genetickou variabilitou?

Odhadněte význam genetické rovnováhy k procesu evoluce?

Testování genetické rovnováhy

Rovnovážný genetický stav v populaci nastává, když platí: 

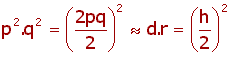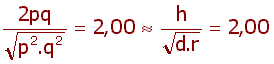Populace je v genetické rovnováze, když frekvence genotypů pozorovaných P (skutečných) se statisticky neliší od frekvencí genotypů za genetické rovnováhy O (očekávané). Na vyhodnocení se používá test dobré shody - (chí kvadrát) test (viz. pravděpodobnost a genetika):

P - pozorované absolutní frekvence genotypů

O - očekávané absolutní frekvence genotypů