Lineární operátory

Operátorem rozumíme zobrazení, které má na vstupu i na výstupu funkci. Například pro funkce jedné proměnné mohou být operátory derivace, druhá derivace, vynásobení funkce funkcí \(\ln x\) anebo vnoření zadané funkce do funkce \(\ln x\). Tj. pro \(y=y(x)\) můžeme uvažovat operátory \(F_1[y]=\frac{\mathrm dy}{\mathrm dx}\), \(F_2[y]=\frac{d^2y}{dx^2}\), \(F_3[y](x)=y(x)\ln(x)\), \(F_4[y](x)=\ln(y(x)).\)

Lineárním operátorem rozumíme zobrazení, které zachovává součet funkcí a násobek konstantou, tj. platí \[L[y_1+y_2]=L[y_1]+L[y_2]\] a \[L[C y_1]=C L[y_1]\] pro libovolné reálné číslo \(C\) a libovolné funkce \(y_1\) a \(y_2\) z definičního oboru operátoru \(L\).

Příklady lineárních operátorů

Linearitu se naučíme využívat k tomu, abychom úlohu najít řešení rovnice rozkouskovali na řešení jednodušších úloh. Například je možné zkombinovat úlohu na stacionární proudění podzemní vody a úlohu na radiální proudění ke studni. Každou z těchto úloh umíme redukovat na separovatelnou diferenciální rovnici a vyřešit. Zkombinováním těchto úloh je možné modelovat chování studny v rovinném toku. Používá se například k zachycení kontaminace spodní vody.

• Operátor derivace, tj. operátor definovaný vztahem \(L[y]=\frac{\mathrm dy}{\mathrm dx}\) je lineární. Toto plyne ze vzorců pro derivaci součtu a konstantního násobku.
• Buď dána funkce \(a(x)\). Operátor násobení funkcí \(a(x)\), tj. \(L[y](x)=a(x)y(x)\) je lineární. To plyne z komutativity násobení a z distributivního zákona (roznásobování závorek).
• Složení (postupná aplikace) lineárních operátorů je lineární operátor. Například tedy \[\frac{\mathrm d^2 y}{\mathrm dx^2}\] je lineární operátor.
• Součet lineárních operátorů je lineární operátor.
• Buď pevně dána funkce \(a(x)\). Lineární operátor \[L[y]=\frac{\mathrm dy}{\mathrm dx}+a(x)y\] se nazývá lineární diferenciální operátor prvního řádu.
• Buďte pevně dány funkce \(p(x)\) a \(q(x)\). Lineární operátor \[L[y]=\frac{\mathrm d^2y}{\mathrm dx^2}+p(x)\frac{\mathrm dy}{\mathrm dx}+q(x)y\] se nazývá lineární diferenciální operátor druhého řádu.
• Buď dána \(n\times n\) matice reálných čísel \(A\) a \(n\)-vektorová funkce \(\vec F(x)\). Zobrazení, které funkci \(\vec F(x)\) přiřadí součin \(A\vec F(x)\) je lineární. To plyne z distributivnosti násobení vzhledem ke sčítání matic a z toho, že součin matice a reálného čísla komutuje.

Princip superpozice

Věta (princip superpozice).

Každý lineární operátor zachovává lineární kombinaci funkcí, tj. platí \[L[C_1 y_1+C_2 y_2]=C_1 L[y_1]+C_2 L[y_2]\] vždy, když \(C_{1,2}\in\mathbb{R}\) a \(y_{1,2}\) jsou funkce z definičního oboru operátoru \(L\).

Plyne přímo rozepsáním \[ \begin{aligned}L[C_1 y_1+C_2 y_2]&= L[C_1 y_1]+L[C_2 y_2]\\ &= C_1 L[y_1]+C_2 L[y_2] \end{aligned} \]

Operátorové rovnice s lineárním operátorem

Operátorovou rovnicí budeme rozumět rovnici \[L[x]=b(t),\] kde \(b(t)\) je funkce a \(L\) operátor.

• Například pro \(b(t)=0\) a \(L[x]=\frac{\mathrm dx}{\mathrm dt}-x\) má rovnice tvar \[\frac{\mathrm dx}{\mathrm dt}-x=0,\] tj. \[\frac{\mathrm dx}{\mathrm dt}=x.\]

Následující věta vlastně vyjadřuje totéž co princip superpozice z předchozího textu, pouze v jiných pojmech: v pojmech řešení rovnice s lineárním operátorem.

Věta (princip superpozice při řešení rovnic).

Jsou-li funkce \(x_1(t)\) a \(x_2(t)\) po řadě řešeními rovnic \[L[x]=b_1(t),\quad L[x]=b_2(t),\] Je funkce \[x(t)=C_1 x_1(x)+C_2 x_2(x)\] řešením rovnice \[L[x]=C_1 b_1(t)+C_2 b_2(t).\]

Pro \(b_1(t)=b_2(t)=0\) všechny tři výše uvedené rovnice splynou a lineární kombinace dvou řešení homogenní lineární rovnice je také řešením. Toto je možné pochopitelně rozšířit na libovolný konečný počet funkcí.

Pro \(b_1(t)=0\) a \(C_2=1\) jsou obě nehomogenní rovnice stejné a pokud k řešení rovnice přičteme řešení asociované homogenní rovnice (se stejným operátorem na levé straně, ale nulou na pravé straně), dostaneme řešení stejné rovnice.

Z těchto jednoduchých tvrzení plyne několik zásadních pozorování.

• Pokud máme k dispozici několik řešení homogenní rovnice, libovolná jejich lineární kombinace je také řešením.
• Za určitých okolností lineární kombinace z předchozího bodu umožní splnit libovolnou počáteční podmínku a vzhledem k jednoznačnosti řešení, která lineární rovnice zpravidla provází, je jistota, že žádné další řešení neexistuje. Nalezení těchto funkcí je tedy zásadní krok při řešení rovnice.
• U nehomogenní rovnice stačí se úloha najít všechna řešení dá rozdělit na dvě dílčí úlohy: najít jenom jedno řešení a k tomu najít všechna řešení homogenní rovnice se stejnou levou stranou. Každá z těchto dvou úloh je mnohem lehčí než úloha celková a součtem jednoho řešení nehomogenní rovnice a obecného řešení asociované homogenní rovnice dostaneme obecné řešení nehomogenní rovnice.

Příklad využití linearity v jedné dimenzi

Pro konkrétnost specifikujeme myšlenky z předchozího textu na příkladě.

Pro jednu funkci lineární kombinace degenerují na násobky. Proto je obecné řešení rovnice součtem jednoho řešení rovnice a obecného řešení asociované homogenní rovnice. Toto jedno řešení vlastně udává pozici v prostoru funkcí a řešení asociované homogenní rovnice udává směr. Například funkce \(x=e^t\) splňuje rovnici \[x'-x=0\] a funkce \(x=-\pi\) splňuje rovnici \[x'-x=\pi.\] Všechna řešení rovnice \[x'-x=\pi\] jsou tvaru \(x=Ce^t-\pi\)

Lineární diferenciální rovnice prvního řádu s konstantními koeficienty

V aplikacích často vídáme rovnici tvaru \[\frac{\mathrm dx}{\mathrm dt}+ax=b,\tag{N}\] která vznikne například úpravou rovnice \[\frac{\mathrm dx}{\mathrm dt}=b-ax.\]
Podobně jako v předchozím příkladě stačí najít jedno řešení rovnice (N) a jedno nenulové řešení rovnice \[\frac{\mathrm dx}{\mathrm dt}+ax=0.\tag{H}\] První z řešení udává bod v prostoru funkcí, druhé řešení jakýsi směr a společně definují jakousi přímku obsahující všechna řešení. Rovnici (N) splňuje konstantní funkce \(x(t)=\frac ba\) a rovnici (H) exponenciální funkce \(x(t)=e^{-at}.\) Obecné řešení rovnice (N) je proto \[x(t)=\frac ba+Ce^{-at}.\] Pro \(t\) jdoucí do nekonečna toto řešení za předpokladu \(a>0\) konverguje ke stacionárnímu řešení \(\frac ba\). Partikulární řešení odpovídající počáteční podmínce \(x(0)=0\) je \[x(t)=\frac ba-\frac bae^{-at}=\frac ba\Bigl(1-e^{-at}\Bigr).\] To znamená, že řešení se exponenciálně přibližuje ke stacionárnímu řešení. Pro \(a<0\) se naopak od stacionárního řešení exponenciálně vzdaluje.

Věta (řešení lineární diferenciální rovnice prvního řádu s konstantními koeficienty).

Obecným řešením rovnice \[\frac{\mathrm dx}{\mathrm dt}+ax=b\] je \[x(t)=x_{\text{st}}+Ce^{-at},\] kde \(x_{\text{st}}=\frac ba\) je stacionárním řešením této rovnice. Pro \(a>0\) je toto řešení stabilní a globálně atraktivní. Pro \(a<0\) je nestabilní.

Obrat, že stacionární řešení je globálně atraktivní znamená, že všechna řešení k tomuto stacionárním stavu konvergují nezávisle na počáteční podmínce.

Lineární autonomní systémy

Následující příklad je mírně modifikovaný příklad z kurzu MIT o diferenciálních rovnicích. Ve formulaci s vařením vajíčka se zdá triviální a prakticky neužitečný. Toto je však voleno pro jednoduchost výkladu a snadnou představu povahy zkoumaného jevu. V praxi se stejným modelem předává teplo vrstveným materiálem (jako je tepelná ochrana domů nebo raketoplánů) nebo chemické látky vstupující do dalších reakcí (jako například řetěz reakcí vedoucí k syntéze bílkovin, které buňka v reakci na okolní prostředí potřebuje k přežití).

Budeme modelovat ohřívání vejce ve vodě o konstantní teplotě \(T_0\). Na počátku mají bílek a žloutek teplotu \(T_1\) a \(T_2\). Žloutek přebírá teplo od bílku rychlostí úměrnou rozdílu teplot žloutku a bílku. Bílek přebírá teplo od vodní lázně rychlostí úměrnou rozdílu teplot a předává teplo žloutku procesem popsaným v předchozí větě. Vody je hodně a její teplota se nemění. Proces můžeme modelovat soustavou diferenciálních rovnic \[\begin{aligned}T_1^\prime &= k_1(T_0-T_1)-k_2(T_1-T_2) \\ T_2^\prime&=k_2(T_1-T_2)\end{aligned}\] Tento systém je možno přepsat do tvaru \[\begin{aligned}T_1^\prime &= -(k_1+k_2)T_1+k_2T_2+T_0k_1 \\ T_2^\prime&=k_2T_1-k_2T_2\end{aligned}\] a zapsat maticově \[\begin{pmatrix}T_1\\T_2\end{pmatrix}'= \begin{pmatrix}-(k_1+k_2) & k_2 \\ k_2 & -k_2\end{pmatrix} \begin{pmatrix}T_1\\T_2\end{pmatrix} + \begin{pmatrix}k_1T_0\\0\end{pmatrix}. \] Pokud zvolíme teplotní stupnici tak, že teplota vroucí vody je v naší nové stupnici nula, můžeme dokonce eliminovat druhý člen a dostáváme \[\begin{pmatrix}T_1\\T_2\end{pmatrix}'= \begin{pmatrix}-(k_1+k_2) & k_2 \\ k_2 & -k_2\end{pmatrix} \begin{pmatrix}T_1\\T_2\end{pmatrix} \tag{V} \] tj. symbolicky \(X'=AX\), kde \(X=(T_1,T_2)^T\) je vektorová funkce (sloupcový vektor) a \(A\) je \(2\times 2\) matice.

Systém \(X'=AX\)

Je-li determinant matice nenulový, má soustava \(AX=0\) pouze nulové řešení a systém \[X'=AX\tag{1}\] má jediné konstantní řešení, kterým je počátek. Konstantní řešení bude nazývat stacionární bod.

Tento systém můžeme přepsat na \[X'-AX=0\] a tento systém je lineární, protože díky distributivnímu zákonu pro matice pro operátor \(L[X]=X'-AX\) platí \[\begin{aligned}L[X_1+X_2]&=(X_1+X_2)'-A(X_1+X_2)\\&=X_1^\prime+X_2^\prime-AX_1 -AX_2\\&=(X_1^\prime -AX_1)+(X_2^\prime-AX_2)\\&=L[X_1]+L[X_2]\end{aligned}\] a díky komutativitě při násobení s konstantou \(C\in\mathbb R\) také \[L[CX]=(CX)'-A(CX)=CX'-CAX=C(X'-AX)=CL[X].\]

Je možné ukázat, že každá počáteční úloha je jednoznačně řešitelná a pro obecné řešení stačí najít tolik nezávislých řešení, kolik komponent má neznámá vektorová funkce \(X\). Platí následující věta, kterou je možno ověřit přímo dosazením.

Věta (souvislost vlastních čísel matice a řešení lineárního autonomního systému).

Má-li matice \(A\) vlastní číslo \(\lambda\) a příslušný vlastní vektor je \(v\), tj. platí \(A v =\lambda v\), je funkce \(X(t)=v e^{\lambda t}\) řešením systému \(X'=AX.\) Jsou-li \(\lambda\) a \(v\) komplexní, je řešením i samostatně reálná část a imaginární část.

Systém \[X'=AX+B\tag{2}\] je možno na tvar (1) převést po přepsání do tvaru \((X-X_0)'=A(X-X_0)\), kde \(X_0\) je řešením soustavy \(AX+B=0\), což odpovídá posunu stacionárního bodu do počátku.

Chování exponenciální funkce je možno prozkoumat numericky zde

Poznámka (vlastní hodnoty a řešení).

Následující poznatky jsou shrnutím a specifikací výše uvedeného a klasifikují stabilitu některých řešení systému (2), tj. \[X'=AX+B.\]

• Jakmile má matice \(A\) reálnou kladnou vlastní hodnotu, existuje řešení, které se vzdaluje od stacionárního bodu směrem daným příslušným vlastním vektorem.
• Jakmile má matice \(A\) reálnou zápornou vlastní hodnotu, existuje řešení, které se přibližuje ke stacionárnímu bodu ze směru daného příslušným vlastním vektorem.
• Jakmile má matice \(A\) komplexní hodnotu s kladnou reálnou částí, existuje řešení, které se v oscilacích vzdaluje od stacionárního bodu.
• Jakmile má matice \(A\) komplexní hodnotu se zápornou reálnou částí, existuje řešení, které se v oscilacích přibližuje ke stacionárnímu bodu.

Pokud jsou například všechna vlastní čísla v daném bodě záporná, poté každé z nich generuje řešení konvergující do stacionárního bodu. Díky linearitě, jednoznačnosti řešení a tomu, že máme tolik řešení, kolik je nutno pro splnění libovolné podmínky, je možné pomocí těchto dílčích řešení zapsat i libovolné jiné řešení. Tím pádem ale všechna řešení konvergují do stacionárního bodu. Pokud jsou vlastní čísla komplexní se zápornou reálnou částí, je situace stejná, ale řešení navíc konvergují do stacionárního bodu postupnými oscilacemi. Podobně, pokud všechny vlastní hodnoty jsou kladné, všechna řešení se od stacionárního bodu vzdalují a pokud jsou všechny vlastní hodnoty komplexní s kladnou reálnou částí, probíhá toto vzdalování oscilacemi s narůstající amplitudou.

Příklad. Model ohřívání vajíčka (V) z předchozí části této přednášky má (v posunuté teplotní stupnici, na které teplota varu vody odpovídá nule) stacionární bod \((0,0)\). Zkusíme zvolit parametry \(k_1\) a \(k_2\) a určit chování trajektorií v okolí tohoto bodu. Pro \(k_1=1\) a \(k_2=2\) dostáváme \[\begin{pmatrix}T_1\\T_2\end{pmatrix}'= \begin{pmatrix}-3 & 2 \\ 2 & -2\end{pmatrix} \begin{pmatrix}T_1\\T_2\end{pmatrix}. \] Vlastní čísla jsou záporná, \(\lambda_{1}=-4.56\) a \(\lambda_{2}=-0.44\) (viz zde). Budou tedy existovat dvě nezávislá řešení konvergující do počátku a všechna další řešení dostaneme jako jejich lineární kombinaci. Proto všechna řešení konvergují k počátku tj. \(T_1=T_2=0\). Obě teploty v naší posunuté stupnici se tedy ustálí na teplotě vodní lázně. Nic jiného jsme ani nečekali, ať mají žloutek a bílek na začátku jakoukoliv teplotu, po čase se teplota ustálí na teplotě vodní lázně. V tomto případě není zajímavé vědět, do jakého stavu systém konverguje, ale například za jak dlouho bude dosaženo potřebné teploty ve žloutku nebo v bílku. V praxi se podobným způsobem neřeší vaření vajec, ale předávání chemických látek jako jsou léky nebo enzymy mezi tkáněmi, prostřednictvím krve. Podobně jako u Newtonova zákona tepelné výměny, i zde je rychlost procesu úměrná množství, v tomto případě úměrná rozdílu koncentrací.

Nelineární autonomní systémy

Soustava diferenciálních rovnic, kde pravé strany nezávisí na čase, se nazývá autonomní systém.

Je-li \(f(X_0)=0\), je možno systém \[X'=f(X)\] v okolí bodu \(X_0\) aproximovat lineárním systémem \[X'=J(X_0)(X-X_0),\] kde \(J(X_0)\) je Jacobiho matice funkce \(f(X)\) v bodě \(X_0\), tj. pro \(f(X)=(f_1(X),\dots,f_n(X))^T\) je \[J(X)=\left(\frac{\partial f_i(X_0)}{\partial x_j}\right).\] O chování trajektorrií v okolí stacionárního bodu tedy rozhodnou vlastní čísla Jacobiho matice. Za předpokladu, že jsme relativně daleko od případů, kdy se mění typ stacionárního bodu, tj. vlastní čísla jsou navzájem různá, jsou nenulová a v případě komplexních vlastních čísel mají nenulové reálné části, má původní nelineární systém stejný typ stacionárního bodu jako lineární systém s Jacobiho maticí. Nelineární systém tedy v jistém smyslu “zdědí” chování řešení od své lineární aproximace pomocí Jacobiho matice. Je však nutno připomenout, že aproximace pomocí Jacobiho matice je jenom lokální a můžeme takto posoudit jenom řešení z nějakého okolí stacionárního bodu.

Zejména tedy, pokud má Jacobiho matice všechny vlastní hodnoty záporné, tak všechna řešení z nějakého okolí stacionárního bodu konvergují do tohoto bodu. Pokud má všechny vlastní hodnoty kladné, všechna řešení z nějakého okolí se naopak od stacionárního bodu vzdalují. To platí i pro vlastní komplexní vlastní hodnoty, pouze se mezi konvergencí a vzdalování přepíná podle znaménka reálné části vlastních hodnot a řešení oscilují směrem ke stacionárnímu bodu nebo od něj.

Poznámka (stabilita a strukturální stabilita řešení).

Stabilitou stacionárního bodu budeme rozumět, stejně jako výše, že malá výchylka od stacionárního bodu vede na řešení, které konverguje zpět k tomuto stacionárnímu bodu. Stabilita vyjadřující, že při malé změně koeficientů v systému se nezmění typ singulárních bodů se nazývá strukturální stabilita.

Bruselátor

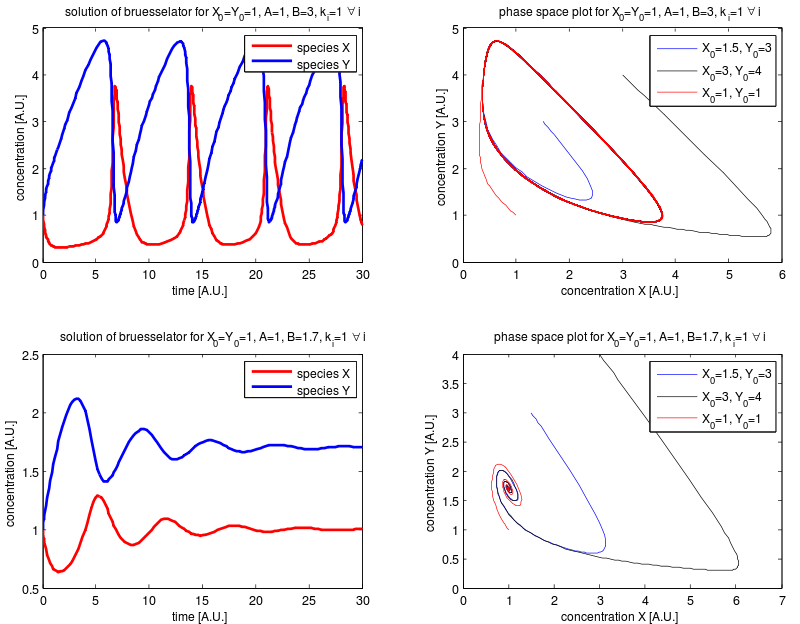
Systém chemických reakcí \[\begin{aligned}A &\rightarrow X\\2X + Y &\rightarrow 3X\\B + X &\rightarrow Y + D\\X &\rightarrow E\end{aligned}\] má pozoruhodnou minulost. První chemickou reakci probíhající podle tohoto schematu objevil ruský chemik B. Bělousov, jeho výsledky přezkoumal a potvrdil A. Žabotinský. Oba zaznamenali překvapivé chování, kdy se periodicky mění koncentrace. Protože to bylo v roce 1951 mimo chápání chemiků, měli potíže s publikováním tohoto převratného jevu. Všeobecně totiž panoval názor, že chemická reakce rychle spěje ke stavu termodynamické rovnováhy a oscilující reakce byla něco jako chemické perpetum mobile. Později vědci (I. Prigogine) sestavili teoretický model periodicky probíhající reakce a po čase několik takových reakcí i našli. Dnes toto chápeme jako jakési chemické hodiny. Název bruselátor je spojení slova Brusel (pracoviště I. Prigogina) a oscilátor.

Pokud je dostatek složek \(A\) a \(B\), modeluje po zjednodušení (viz Wikipedie, konstanty úměrnosti klademe rovny jedné) chemické reakce soustava \[ \begin{aligned} \frac {\mathrm d X}{\mathrm dt}&= A + X ^2 Y - B X - X,\\ \frac {\mathrm d Y}{\mathrm dt}&= BX-X^2Y, \end{aligned} \] kde \(X\) pro jednoduchost znamená koncentraci látky \(X\) a totéž platí i pro další veličiny vystupující v rovnici.

Stacionárním bodem je bod \(X=A\), \(Y=\frac BA\). Pro \(A=1\) a \(B=4\) má systém tvar \[ \begin{aligned} \frac {\mathrm d X}{\mathrm dt}&= X ^2 Y - 5 X,\\ \frac {\mathrm d Y}{\mathrm dt}&= 4X-X^2Y, \end{aligned} \]

Jacobiho matice je \[J(X,Y)=\begin{pmatrix}2XY-5 & X^2 \\ 4-2XY & -X^2\end{pmatrix}\] a \[J(1,4)=\begin{pmatrix}3& 1\\-4 & -1\end{pmatrix}.\] Vlastní čísla jsou řešením rovnice \[0=\begin{vmatrix}3-\lambda & 1\\-4 & -1-\lambda\end{vmatrix} =\lambda^2- 2\lambda+4=(\lambda-1)^2+3.\] Taková rovnice nemá řešení v množině reálných čísel a vlastní čísla jsou komplexně sdružená \[\lambda_{1,2}=1\pm \sqrt {3}i.\] Protože reálná část \(\Re(\lambda_i)=1>0\), řešení se v oscilacích vzdalují od rovnovážného bodu. Protože systém je druhého řádu a tímto postupem je možno získat dvě nezávislá řešení, lineárními kombinacemi vygenerujeme všechna řešení. Proto se v oscilacích budou od stacionárního bodu vzdalovat všechna řešení. Další stacionární bod neexistuje a koncentrace určitě zůstanou ohraničené z fyzikálních důvodů. Proto neexistuje stabilní stav, a systém je nestabilní. Je možné ukázat, že systém není chaotický, ale oscilacemi se přibližuje k periodickému řešení. Taková analýza je však již nad rámec základního seznámení se s aparátem autonomních systémů.

Autonomní systém ve dvou dimenzích

Ve dvou dimenzích je autonomní systém možno psát ve tvaru \[ \begin{aligned} x'=f(x,y),\\ y'=g(x,y). \end{aligned}\] Pro autonomní systémy v rovině používáme dva základní způsoby vizualizace. Oba si můžete prohlédnout výše v příkladu s bruselátorem.

1. Řešení zobrazíme jako grafy funkcí \(x(t)\) a \(y(t)\). Tímto přístupem dokážeme posoudit dynamiku v čase, odhadnout rychlost s jakou se mění obě komponenty řešení. Často kreslíme do jednoho obrázku a často máme v tomto obrázku dvojí souřadnicový systém: jeden pro hodnoty \(x\) a jeden pro hodnoty \(y\).
2. Řešení zobrazíme jako parametrickou křivku \(\vec r(t)=[x(t), y(t)]\). Tato křivka se nazývá trajektorie. V tomto případě sice nemáme informaci o dynamice v čase, ale můžeme lehce posoudit, jak se chovají řešení vycházející z různých počátečních podmínek. Proto tento způsob zpravidla preferujeme. Tento způsob znázornění se nazývá fázový portrét.

Křivky tvořené trajektoriemi mají speciální vlastnosti. Například se díky jednoznačné řešitelnosti nemohou dvě různé trajektorie protnout. Díky tomu existuje jenom několik málo druhů trajektorií.

• Stacionární body. Tyto body odpovídají konstantním řešením.
• Uzavřené trajektorie, cykly. Tyto trajektorie odpovídají periodickým řešením. Uvnitř každého cyklu leží alespoň jeden stacionární bod.
• Trajektorie, které samy sebe nikde neprotínají a pro \(t\to\pm\infty\) tyto trajektorie mají jednu z následujících vlastností.
  • Trajektorie mají alespoň jednu složku neohraničenou.
  • Trajektorie konvergují k některému ze stacionárních bodů.
  • Trajektorie konvergují k některému z cyklů.
  • Trajektorie konvergují k množině tvořené konečným počtem singulárních bodů a jinými trajektoriemi, které vedou z jednoho stacionárního bodu do druhého. S tímto typem trajektorií se však v jednoduchých modelech nesetkáme.

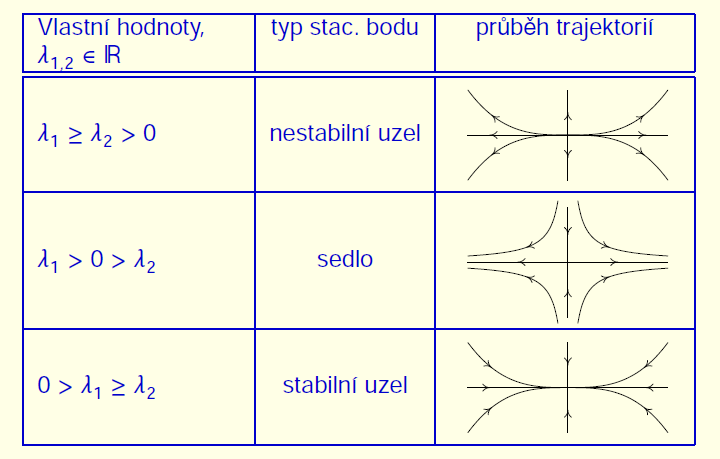
Podle chování trajektorií v okolí stacionárních bodů rozdělujeme tyto stacionární body do několika navzájem disjunktních skupin. Dokážeme je identifikovat pomocí vlastních hodnot Jacobiho matice vypočtené v tomto stacionárním bodě.

• Stabilní uzel je stacionární bod takový, že pro \(t\to\infty\) všechny trajektorie z nějakého okolí konvergují do tohoto bodu bez oscilací. Nestabilní uzel má stejnou vlastnost, ale pro \(t\to-\infty\). Stabilní uzel poznáme podle dvou záporných a nestabilní uzel podle dvou kladných reálných vlastních hodnot.
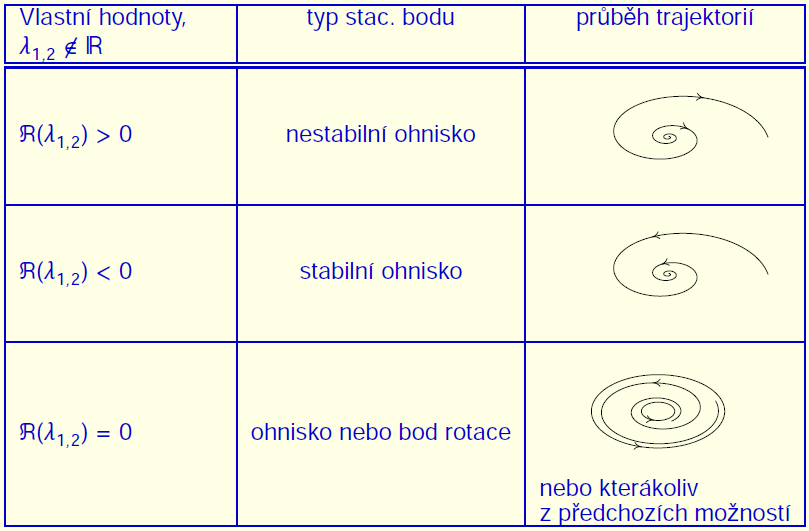
• Stabilní a nestabilní ohnisko je stacionární bod se stejnou vlastností jako uzel, ale konvergence je spojena s oscilacemi okolo stacionárního bodu. Stabilní ohnisko poznáme podle dvou komplexně sdružených vlastních hodnot se zápornou reálnou částí, nestabilní ohnisko s kladnou reálnou částí.
• Sedlo je stacionární bod, který má v každém okolí pouze konečný počet trajektorií, které pro \(t\to\pm\infty\) konvergují k tomuto bodu. Poznáme jej podle jedné kladné a jedné záporné vlastní hodnoty.
• Bod rotace je takový bod, v jehož každém okolí jsou cykly. Pokud navíc v nějakém okolí existují pouze cykly, nazývá se tento bod navíc střed. Bod rotace souvisí s komplexně sdruženými vlastními čísly s nulovou reálnou částí, ale v těchto případech může stacionární bod být i ohniskem.

Vícerozměrné autonomní systémy, kompartmentové modely

Kompartmentové modely jsou modely, kde se je studovaná veličina rozdělena do několika stavů a mezi těmito stavy se v jakémsi smyslu přelévá definovanou rychlostí. Klasickým případem v roce 2020 je model epidemie, například SIR model nebo SEIR model.