Inverzní matice, determinanty
Robert Mařík
2020-2021
- Inverzní matice
- Matice přechodu
- Zobrazení v různých soustavách souřadnic
- Praktická aplikace: transformace tenzoru
- Obecné vzorce pro transformaci tenzoru
- Role vlastních vektorů při transformaci matic
- Transformace symetrické matice na diagonální tvar
- Determinant matice
- Determinant matice \(2\times 2\) (křížové pravidlo)
- Determinant matice \(3\times 3\) (Sarusovo pravidlo)
- Determinant matice ve schodovitém tvaru
- Souvislost některých pojmů
- Hookův zákon, matice tuhosti a poddajnosti
- Vlastní vektory matice a matice inverzní
- Shrnutí, hlavní myšlenky
Motivace.
- Chování libovolného systému nezávisí na souřadné soustavě, ve které tento systém popisujeme. Opravdu, dřevo neví, jak jsme si zvolili osy soustavy souřadnic. Ani, zda používáme pravoúhlou soustavu či jinou. Už vůbec dřevo nepozná, zda úlohu řešíme v pravotočivé či levotočivé soustavě souřadnic. Vhodná volba souřadné soustavy přirozeně neovlivní chování systému. Může ale značně usnadnit výpočty. Proto například při studiu obdélníkového objektu volíme osy ve směru hran. Proto například při studiu dřeva volíme souřadné osy v anatomických směrech dřeva. Tyto dva požadavky jsou částečně proti sobě v případě, že studujeme obdélníkový materiál s hranami jdoucími jiným směrem, než jsou anatomické směry dřeva. Naučíme se s tímto probléme vypořádat. Naučíme se používat matice k přechodu mezi souřadnými soustavami. Naučíme se transformovat fyzikální vlastnosti popsané maticemi z jedné soustavy do druhé.
- Ukázali jsme si, že soustavu lineárních rovnic je možné zapsat pomocí maticového násobení ve tvaru \(AX=B\). Pokud by veličiny v této rovnici byla reálná čísla, řešitelnost je značně ovlivněna nulovostí či nenulovostí veličiny \(A\). Ukážeme si zobecnění této vlastnosti i pro matice a soustavy rovnic. K tomu si představíme nový pojem - determinant matice.
Inverzní matice

U reálných čísel máme doplňkové operace ke sčítání a násobení. Jsou to odečítání a dělení. Odečítání matic můžeme implementovat jako sčítání matice s maticí vynásobenou minus jedničkou: \(A-B=A+(-B)\). Oproti tomu operace dělení matic vůbec není implementována. U reálných čísel lze dělení nahradit násobením převrácenou hodnotou: \(\frac {a}{b}=ab^{-1}\). Tuto proceduru částečně rozšíříme pro matice. Připomeňme ještě, že roli neutrálního prvku při násobení matic hraje jednotková matice. Například pro matice \(3\times 3\) je jednotková matice \[ I= \begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix} . \]
Definice (inverzní matice).
Buď \(A\in\mathbb R^{n\times n}\) čtvercová matice řádu \(n\). Jestliže existuje čtvercová matice \(A^{-1}\) řádu \(n\), splňující vztahy \[A^{-1}A=I=A A^{-1},\] nazýváme matici \(A^{-1}\) inverzní maticí k matici \(A\).
Poznámka. Předchozí definice nezaručuje existenci inverzní matice. K některým čtvercovým maticím inverzní matice existuje, k některým ne. Později uvidíme, že existuje jednoduchá charakterizace matic, ke kterým inverzní matice existuje, pomocí determinantu matice.
Věta (inverze maticového součinu).
Inverzní matice k součinu dvou matic je součinem jednotlivých inverzních matic, ale v opačném pořadí, tj. \[(AB)^{-1}=B^{-1}A^{-1}.\]

Příklad. Pomocí matic a jejich součinu je možné zapsat libovolnou permutaci konečněprvkové množiny. Známým permutačním hlavolamem je Rubikova kostka. Na ní snadno vidíme, že pokud kostku zamícháme ze složeného stavu tahem v horní stěně a poté v pravé stěně, pro opětovné složení musíme vracet tahy v opačném pořadí, tj. nejdřív vrátit tah v pravé stěně a poté ve stěně horní. Pěkně to jde vidět na následující animaci, kterou můžete spustit nebo přehrávat po jednotlivých krocích. Na druhou stranu, tato vlastnost se dá využít k vyřešení Rubikovy kostky naprosto bez algoritmů, protože při vhodně zvolených tazích ovlivníme jenom málo kostiček, například jenom tři.
Inverzní matice k matici popisující rotaci v rovině
Pro matici rotace \[R_\theta=\begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix}\] z minulé přednášky platí \[(R_\theta)^{-1}=R_{-\theta} = \begin{pmatrix} \cos(-\theta) & -\sin (-\theta)\\ \sin(-\theta) & \cos(-\theta) \end{pmatrix} = \begin{pmatrix} \cos\theta & \sin \theta\\ -\sin\theta & \cos\theta \end{pmatrix}\] což je přirozené pokud si uvědomíme, že inverzní operací k pootočení roviny o úhel \(\theta\) je pootočení roviny o úhel opačný.
Odsud mimo jiné vidíme, že platí \[(R_\theta)^{-1}=\begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix}^{-1}=\begin{pmatrix} \cos\theta & \sin \theta\\ -\sin\theta & \cos\theta \end{pmatrix} =\begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix}^T=(R_\theta)^T,\] tj. že inverzní a transponovaná matice jsou v případě matice rotace stejné. To je velká náhoda, ale přesto matice s touto vlastností hrají tak důležitou roli, že si vysloužily vlastní název představený v následujícím odstavci.
Ortogonální matice
Definice (ortogonální matice).
Ortogonální matice je matice, jejíž transponovaná matice je současně maticí inverzní.
Řádky ortogonální matice jsou tvořeny navzájem kolmými vektory jednotkové délky. Má-li například symetrická čtvercová matice \(A\) řádu \(n\) celkem \(n\) lineárně nezávislých jednotkových vlastních vektorů, potom matice vytvořená tak, že sloupce nebo řádky matice jsou tyto vektory, je ortogonální.
Matice přechodu


Ukážeme si, že pomocí matic je možné přepočítávat souřadnice mezi jednotlivými souřadnými soustavami. Praktické využití je studium ortotropních materiálů v situace, kdy pro matematický popis jsou výhodné směry os, ale roviny symetrie neodpovídají souřadným rovinám. Například dřevěný kvádr je vhodné studovat tak, že hrany kvádru jsou rovnoběžné se souřadnými osami. Materiálové vlastnosti jsou známy v anatomických směrech dřeva. Pokud tyto směry nejsou nejsou rovnoběžné s osami (kvádr je nařezaný našikmo), je potřeba mezi souřadnými soustavami přecházet. To se dá elegantně udělat pomocí maticového násobení a inverzní matice.
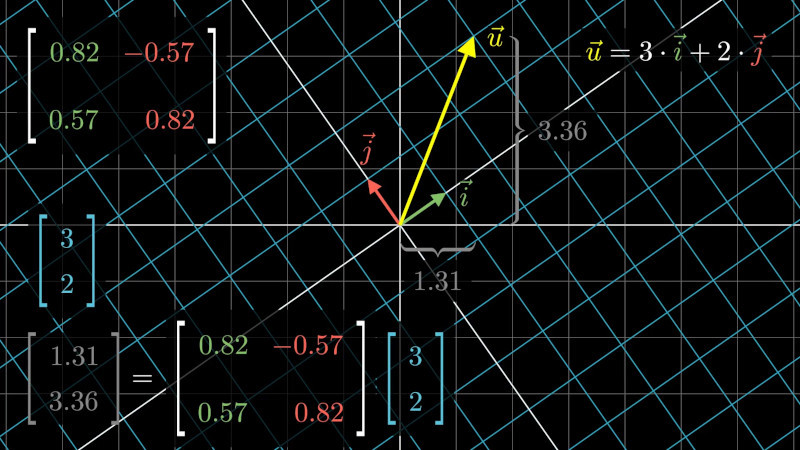
Předpokládejme, že v rovině jsou dány dvě kartézské soustavy souřadnic \(\mathcal B\) a \(\mathcal B'\), které jsou vzájemně pootočené o úhel \(\theta\). V těchto soustavách budou souřadnice \((x,y)^T\) a \((x',y')^T\). Je-li soustava \(\mathcal B'\) otočená oproti soustavě \(\mathcal B\) o úhel \(\theta\) proti směru hodinových ručiček, má (viz obrázek) jednotkový vektor ve směru osy \(x'\) v bázi \(\mathcal B\) souřadnice \((\cos(\theta),\sin(\theta))^T\) a jednotkový vektor ve směru osy \(y'\) má v bázi \(\mathcal B\) souřadnice \((-\sin(\theta),\cos(\theta))^T\). Proto je vztah mezi souřadnicemi dán maticovým součinem \[\begin{pmatrix}x\\y\end{pmatrix}_{\mathcal B}= \begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix}x'\\y'\end{pmatrix}_{\mathcal B'}. \] Matice \[R=\begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix}\] je matice, kterou jsme poznali jako matici rotace. Je to matice, která svým působením pootočí vektor který ji násobí zprava o úhel \(\theta\) proti směru hodinových ručiček. Ve výše uvedením kontextu se tato matice nazývá maticí přechodu mezi oběma uvažovanými souřadnými systémy. Matice přechodu umožňuje najít souřadnice vektoru v jedné souřadné soustavě pomocí souřadnic vektoru v souřadné soustavě vzniklé pootočením díky vztahu \[\begin{pmatrix}x\\y\end{pmatrix}_{\mathcal B}= R\begin{pmatrix}x'\\y'\end{pmatrix}_{\mathcal B'}. \] Tato matice má inverní matici a proto evidentně můžeme mezi souřadnicemi přecházet i v opačném směru vztahem \[R^{-1}\begin{pmatrix}x\\y\end{pmatrix}_{\mathcal B} = \begin{pmatrix}x'\\y'\end{pmatrix}_{\mathcal B'}. \]
V inženýrských problémech je častou aplikací lineární algebry transformace úlohy do vhodných souřadnic, ve kterých je popis jednodušší. Zpravidla se jedná o prosté otočení. Toto se používá při studiu dřeva, které má anatomicky význačné směry, při studiu vrstvených materiálů, při studiu chování vodorovně uložených geologických vrstev. Nemusí však vždy jít jenom o materiál s charakteristickými směry. Transformace mezi souřadnicemi se používá například v letectví, kdy je jedna souřadná soustava spojena s trupem a další dvě jsou pootočené ve směru křídel šípovitě připojených k trupu.
Matici transformace popisující otočení souřadnic budeme zkráceně označovat \(R\), pokud budeme potřebovat zdůraznit velikost úhlu, použijeme \(R(\theta)\) a pokud budeme potřebovat matici rozepsat ve složkách, budeme zkracovat výrazy \(\cos\theta\) a \(\sin\theta\) na \(C\) a \(S\) a psát \[R= \begin{pmatrix} C & -S \\ S & C \end{pmatrix}. \] Potom například platí \[R^{-1}= \begin{pmatrix} C & S \\ -S & C \end{pmatrix}. \]
Zobrazení v různých soustavách souřadnic
Ukážeme si důležité využití matice přechodu. Předpokládejme, že máme zobrazení \(f\colon X\to Y\), které je možno charakterizovat maticemi. Na vstupu i výstupu je tedy vektor. Může se jednat třeba o zobrazení, které působícím silám přiřadí deformaci tělesa, což uvidíme v Hookově zákoně později. Může se jednat také o zobrazení, které vektoru charakterizujícímu změnu tlaku v podzemní vodě nebo změnu koncentrace vody ve dřevě přiřadí směr proudění. (Směr podnětu a výsledného proudění si nemusí odpovídat, protože voda je poháněna rozdílem tlaků ve směru největšího poklesu tlaku nebo rozdílem koncentrací ve směru největšího poklesu koncentrace, ale současně si v anizotropním prostředí hledá cestu nejmenšího odporu).
Nechť je naše zobrazení vyjádřeno v nějaké souřadné soustavě \(\mathcal B\) maticí \(A\), tj. \[Y=AX,\] kde \(X\) a \(Y\) jsou souřadnice vzoru a obrazu v souřadné soustavě \(\mathcal B\). Budeme chtít toto zobrazení vyjádřit v jiné soustavě. Například v soustavě \(\mathcal B'\) takové, že platí \(X=PX'\) a \(Y=PY'\), kde čárkovaná písmena jsou souřadnice v čárkované souřadné soustavě \(\mathcal B'\). Dosazením získáme \[PY'=APX'\] a po vynásobení inverzní maticí \[P^{-1}(PY')=P^{-1}(APX'),\] tj \[Y'=(P^{-1}AP)X'.\] V pootočených souřadnicích \(\mathcal B'\) je tedy zobrazení charakterizováno maticí \(P^{-1}AP\). Pro vhodně zvolenou matici \(P\) může být matice v nové bázi podstatně jednodušší než matice v bázi původní.
Častým úkolem je zapsat vztahy mezi veličinami tak, aby byly co nejjednodušší a proto jeden z častých úkolů v lineární algebře bývá takovou šikovnou bázi nalézt. Nastíníme neoptimističtější variantu postupu, případné detaily a řešení zádrhelů je možné najít v odborné literatuře. Zpravidla vyjadřujeme zobrazení v bázi tvořené ortonormálními vlastními vektory matice \(A\). Sloupce matice \(P\) jsou vlastní vektory matice \(A\). Pokud je matice \(A\) symetrická, je matice \(P\) navíc ortogonální, její inverze je tedy matice transponovaná. Tomuto procesu se říká diagonalizace matice, protože \(P^{-1}AP\) vychází diagonální a v diagonále vychází právě vlastní čísla matice.
Stejným způsobem se transformují i fyzikální veličiny veličiny popisované maticemi, nazývané tenzory.
Praktická aplikace: transformace tenzoru



V knize A. Požgaj a kol., Štruktúra a vlastnosti drevá, je následující úloha (str. 322, vydání 1997, ISBN 80-07-00960-4). Dřevo v konfiguraci podle obrázku je namáháno pouze tahovou silou svisle, tedy tenzor napětí má jenom jednu nenulovou složku. Naším cílem je pootočit souřadnou soustavu tak, aby byl tenzor napětí vyjádřen v anatomických směrech dřeva. Úloha je v knize vyřešena pomocí směrových kosinů. Ukážeme si alternativní způsob, který je výhodný v tom, že využívá pouze základní aparát lineární algebry. Původní souřadnice \((x_1,x_2)\) označíme \((x,y)\), osa \(x\) směřuje vodorovně vpravo (v obrázku \(x_2\)) a osa \(y\) nahoru (v obrázku \(x_1\)). Tenzor napětí je \(A= \begin{pmatrix} 0 & 0\\0& 10 \end{pmatrix}\) (tah pouze ve směru osy \(y\)). Souřadnice je nutno pootočit o \(30\) stupňů po směru hodinových ručiček, tj. v záporném směru. Nový tenzor napětí (viz Sage nebo Python) je \[R(30^\circ)AR(-30^\circ)= \begin{pmatrix} 2.5 & -4.3\\ -4.3& 7.5 \end{pmatrix}.\] V nových souřadnicích je směr \(y'\) podélný a proto \(\sigma_{RR}=2.5\) a \(\sigma_{LL}=7.5\). Mimodiagonální složka udává komponentu \(\sigma_{RL}=-4.3\), smykové napětí. Tento výsledek je stejný, jako výsledek získaný jiným postupem v knize, pomocí směrových kosinů. Použili jsme však jenom základní nástroje lineární algebry.
Výše uvedený výpočet se používá, když chceme najít deformaci vyvolanou působícím napětím. Protože konstanty udávající materiálovou odezvu máme změřeny v anatomických směrech dřeva, je nutno nejprve zjistit, jaké namáhání je v těchto směrech, pomocí materiálových konstant zjistíme, jaká je deformace v těchto směrech a poté zpětnou transformací přepočítáme tuto deformaci do původních souřadnic.
Stejný výpočet používáme, pokud se snažíme transformovat působící napětí při posouzení, jaké smykové a jaké normálové napětí působí na šikmý lepený spoj. Pokud je spoj pod úhlem \(30\) stupňů a v ose \(y\) působí tahové napětí \(10\,\mathrm{MPa}\), potom normálové napětí namáhající tento spoj je \(7.5\,\mathrm{MPa}\) a smykové napětí \(4.3\,\mathrm{MPa}\).
Obecné vzorce pro transformaci tenzoru

Úloha na transformaci tenzoru, kterou jsme řešili v minulém odstavci je v aplikacích velmi důležitá. Proto existuje řada grafických nebo inženýrských metod na řešení tohoto úkolu. Tyto metody jsou důvtipné a názorné, například metoda Mohrovy kružnice, oproti lineární algebře však mají zásadní nevýhodu: uživatel se musí stále učit něco nového a dostává návod “jak”, nikoliv “proč”. Použitím aparátu lineární algebry, stejně jako dokážeme v pootočených souřadnicích vyjádřit libovolné zobrazení, dokážeme vyjádřit v pootočených souřadnicích i libovolný tenzor. Vzorce jsou stejné a navíc při otočení v rovině je matice rotace ortogonální, tj. inverzní matice je maticí transponovanou. Pro symetrický tenzor \(A= \begin{pmatrix} a_{11} & a_{12} \\ a_{12} & a_{22} \end{pmatrix}\) dostáváme v souřadnicích otočených o úhel \(\theta\) proti směru hodinových ručiček \[\begin{pmatrix} a'_{11} & a'_{12} \\ a'_{12} & a'_{22} \end{pmatrix} = \begin{pmatrix} C&S\\-S&C \end{pmatrix} \begin{pmatrix} a_{11} & a_{12} \\ a_{12} & a_{22} \end{pmatrix} \begin{pmatrix} C&-S\\S&C \end{pmatrix}, \] kde po výpočtu \[ \begin{aligned} a'_{11}&=C^2a_{11} + S^2a_{22} + 2CSa_{12},\\ a'_{22}&=S^2a_{11} + C^2a_{22} - 2CSa_{12},\\ a'_{12}&=-CSa_{11} + CSa_{22} + (C^2 - S^2)a_{12}. \end{aligned}\tag{*} \] Tento vztah je lineání vzhledem ke všem komponentám a je možné jej zapsat pomocí maticového násobení \[ \begin{pmatrix} a'_{11}\\a'_{22}\\a'_{12} \end{pmatrix} = \begin{pmatrix} C^2 & S^2 & 2CS\\ S^2 & C^2 & -2CS\\ -CS & CS & C^2-S^2 \end{pmatrix} \begin{pmatrix} a_{11}\\a_{22}\\a_{12} \end{pmatrix}. \] Tento vztah je uveden i v literatuře A. Požgaj a kol., Štruktúra a vlastnosti drevá, a v e-opoře Fyzikální a mechanické vlastnosti dřeva. Zde je také uvedena jedna z aplikací, transformace tenzoru deformací naměřených při bobtnání dřeva. V této úloze je nutno tenzor deformací transformovat do anatomických směrů dřeva. To je možné udělat po změření sklonu vláken a pootočení tenzoru o příslušný úhel.
Inverzní operací je pootočení o úhel \(-\theta\) a proto je snadné najít inverzní transformaci: vzhledem k sudosti funkce \(\cos\) a lichosti funkce \(\sin\) stačí změnit znaménko u členů s \(S\), tj. \[ \begin{pmatrix} a_{11}\\a_{22}\\a_{12} \end{pmatrix} = \begin{pmatrix} C^2 & S^2 & -2CS\\ S^2 & C^2 & 2CS\\ CS & -CS & C^2-S^2 \end{pmatrix} \begin{pmatrix} a'_{11}\\a'_{22}\\a'_{12} \end{pmatrix}. \]
Poznámka. Pokud vypočteme derivaci členů \(a'_{11}\) a \(a'_{22}\) podle \(\theta\), dostaneme použitím \[\frac{\mathrm d}{\mathrm d\theta}C^2=\frac{\mathrm d}{\mathrm d\theta}\cos^2\theta=2\cos\theta(-\sin\theta)=-2CS,\] a analogicky \(\frac{\mathrm d}{\mathrm d\theta}S^2=2SC\), \(\frac{\mathrm d}{\mathrm d\theta}CS=-S^2+C^2\) derivace \[ \begin{aligned} \frac{\mathrm d a'_{11}}{\mathrm d\theta}&= -2CSa_{11}+2SCa_{22}+2(C^2-S^2)a_{12}=2a'_{12},\\ \frac{\mathrm d a'_{22}}{\mathrm d\theta}&= 2SCa_{11}-2CSa_{22}+2(S^2-C^2)a_{12}=-2a'_{12}.\\ \end{aligned} \] To znamená, že lokální extrémy diagonálních prvků nastávají v okamžiku, kdy jsou prvky mimo diagonálu nulové. Toto pozorování perfektně ladí s výsledky, které známe v lineární algebře i bez hledání lokálních extrémů a bez derivací. Náznak tohoto konceptu si představíme na dalších stránkách. Budeme potřebovat vlastní vektory matice.
Pozor. V případě tenzoru deformace se někdy se namísto mimodiagonální komponenty bere její dvojnásobek, protože ten má názorný význam jako úhel smyku. Proto se někdy v literatuře uvádí transformační vzorec pro deformace v upraveném tvaru, kdy u složek se součinem \(CS\) ve třetím sloupci není koeficient \(2\) a u odpovídajících složek ve třetím řádku tento koeficient naopak figuruje. Je proto potřeba dávat pozor na to, s jakými komponentami je tenzor malých deformací uvažován.
Role vlastních vektorů při transformaci matic

Budeme zkoumat, kdy platí \[P^{-1}AP=D\] pro čtvercové matice \(P\), \(A\) a diagonální čtvercovou matici \(D\). Vynásobením maticí \(P\) zleva dostaneme \[AP=PD.\] Ve cvičení jsme násobili čtvercovou matici s maticí diagonální a není těžké vidět obecný princip, že matice \(PD\) má za sloupce násobky sloupců matice \(P\) s odpovídajícím číslem z hlavní diagonály matice \(D\). Například pro první sloupec matice \(P\) a první číslo v hlavní diagonále matice \(D\), které označíme \(\vec p_1\) a \(\lambda_1\), dostáváme \[A\vec p_1=\lambda_1 \vec p_1,\] tj. (viz předchozí přednášky) \(p_1\) je vlastní vektor matice \(A\) příslušný vlastní hodnotě \(\lambda_1\). Podobný princip platí pro všechny sloupce. Je otázkou, jestli vlastních hodnot a vlastních vektorů je tolik, kolik pro diagonalizaci “potřebujeme”. Částečně pozitivní odpověď na tuto otázku udávají věty na následujícím slidu.
Transformace symetrické matice na diagonální tvar
Věta (vlastní čísla symetrické matice).
Symetrická čtvercová matice \(A\) řádu \(n\) má \(n\) reálných vlastních čísel (počítáno i s případnou násobností).
Věta (diagonalizace symetrické matice).
Nechť má symetrická čtvercová matice \(A\) řádu \(n\) celkem \(n\) reálných různých vlastních čísel \(\lambda_i\). Označme odpovídající vlastní vektory jednotkové délky \(\vec v_i\).
- Matice \(P\) sestavená tak, že sloupce této matice jsou tvořeny vektory \(\vec v_i\) je ortogonální.
- Matice \(D\) definovaná vztahem \[D=P^TAP\] je diagonální.
- Diagonální prvky matice \(D\) jsou právě vlastní čísla \(\lambda_i\) a jsou ve stejném pořadí jako odpovídající vlastní vektory v matici \(P\).
Poznámka (diagonální tvar materiálových vlastností dřeva).
Typickým ortotropním materiálem je dřevo. Pokud transformujeme tenzor difuzní matice pro dřevo na diagonální tvar, jsou diagonální prvky v poměru přibližně \(D_L:D_R:D_T=35:3:2\) (P. Horáček, Fyzikální a mechanické vlastnosti dřeva, 2008 , str. 65). Ortotropní charakter má však nejenom transport tekutin, ale i sesychání a bobtnání. V tomto případě však naopak v podélném směru dřevo bobtná nejméně a tenzor popisující bobtnání má po transformaci na diagonální tvar v diagonále prvky v poměru přibližně \(\alpha_T:\alpha_R:\alpha_L=20:10:1\) (P. Horáček, Fyzikální a mechanické vlastnosti dřeva, 2008 , str. 38).
Matice transformace \(P\) z předchozí věty je ortogonální (její transponovaná matice je současně její inverzní matice) a její determinant (veličina, se kterou se seznámíme vzápětí) je roven \(1\) nebo \(-1\). Pokud je determinant kladný, reprezentuje matice pootočení soustavy souřadnic. Pokud je determinant záporný, jedná se o pootočení spojené se zrcadlením jedné osy. Protože tento případ většinou z fyzikálních důvodů nepreferujeme, sestavujeme matici transformace tak, aby měla determinant kladný. V případě záporného determinantu stačí prohodit dva vektory (sloupce matice transformace) mezi sebou, nebo jeden vynásobit faktorem \(-1\).
Pro kontrolu je zajímavé vědět, že determinant matice se pootočením nemění a je tedy stejný pro původní i transformovanou matici. Totéž platí pro součet prvků v hlavní diagonále (v lineární algebře se nazývá stopa matice), pro charakteristický polynom a pro vlastní hodnoty. Tenzor, jak jej uvažujeme v tomto textu, je matice, která má navíc fyzikální význam a vzhledem ke své povaze pro ni platí speciální transformační pravidla. Nicméně je to mimo jiné i matice a proto vše výše uvedené platí i pro tenzory.
Transformace tenzorů je užitečná a důležitá činnosti. Bohužel však vzorce s touto transformací spojené nejsou natolik zapamatovatelné, aby bylo obvyklé s nimi pracovat. Možnosti jsou v zásadě tři.
- Mít vzorce v psané podobě po ruce a pouze do nich dosazovat.
- Mít k dispozici jednoduše zapamatovatelný postup, jak s transformacemi pracovat. Takový postup existuje, nazývá se Mohrova kružnice a po zapracování se jedná o efektivní grafickou metodu pro transforamci tenzorů. Zpravidla je v literatuře popsána pro tenzor napětí, funguje však obecně.
- Pracovat pouze s elementárními prostředky lineární algebry. Narozdíl od předchozích bodů máme přehled o tom, co a proč děláme (oproti vzorcům) a nemusíme se učit další metodu (oproti Mohrově kružnici).
Determinant matice
Definice (determinant).
Buď \(A\in\mathbb R^{n\times n}\) čtvercová matice řádu \(n\). Determinant matice \(A\) je reálné číslo \({\det A}\) přiřazené matici \(A\) následujícím způsobem:
- Je-li \(A\) matice řádu \(1\), tj. \(A=(a_{11})\), je \(\det A=a_{11}\).
- Máme-li definován determinant z matice řádu \((n-1)\) označme symbolem \(M_{ij}\) determinant matice řádu \((n-1)\), která vznikne z matice \(A\) vynecháním \(i\)-tého řádku a \(j\)-tého sloupce. Definujme algebraický doplněk \(A_{ij}\) prvku \(a_{ij}\) jako součin \(A_{ij}=(-1)^{i+j}M_{ij}\).
- Konečně, definujme determinant řádu \(n\) následovně: zvolíme libovolný index \(i\in\{1,2,\dots n\}\) a definujeme \[ \det A= a_{i1}A_{i1}+ a_{i2}A_{i2}+\cdots+ a_{in}A_{in}. \]
Uff. Zacházejme vyjímečně s touto definicí stejně jako s definicí limity: vezmeme na vědomí, že nějaká korektní definice existuje, ale učit se ji nebudeme. Není to totiž tak úplně potřeba. bude nám stačit naučit se několik málo speciálních případů.
Determinant matice \(A\) označujeme též \(|A|\). Je-li \(A=(a_{ij})\) píšeme zkráceně \(|a_{ij}|\) místo \(|(a_{ij})|\). K záměně s absolutní hodnotou může dojít jedině v případě, že matice \(A\) je řádu jedna. V praxi se však obvykle s maticemi řádu jedna nepracuje.
Definice (regulární a singulární matice).
Buď \(A\) čtvercová matice. Je-li \(\det A=0\), říkáme, že matice \(A\) je singulární, v opačném případě říkáme, že je regulární.
Determinant matice \(2\times 2\) (křížové pravidlo)
\[ \begin{vmatrix} a &b\\ c& d \end{vmatrix} =ad-bc \]
Tento determinant je roven nule právě tehdy, když je jeden řádek matice násobkem druhého a to bude právě tehdy když je jeden sloupec matice násobkem druhého.
Determinant matice \(3\times 3\) (Sarusovo pravidlo)
\[ \begin{vmatrix} a&b&c\\ i&j&k\\ x&y&z \end{vmatrix} =ajz+bkx+ciy-(cjx+biz+aky) \]
Mnemotechnická pomůcka: opsat první dva řádky pod determinant, vynásobit hlavní diagonálu a dvě diagonály pod tím, potom vynásobit vedlejší diagonálu a dvě diagonály pod tím. Příspěvky od hlavní diagonály a dvou šikmých řad pod ní se sčítají, příspěvky od vedlejší diagonály a dvou šikmých řad pod ní se odečítají.
Determinant matice ve schodovitém tvaru
Definice (schodovitý tvar).
Řekneme, že matice \(A\) je ve schodovitém tvaru, jestliže případné nulové řádky jsou uspořádány na konci matice a nenulové jsou uspořádány tak, že každý následující řádek začíná větším počtem nul než řádek předchozí.
Příklad. Matice \[ \begin{pmatrix} 4& 7 &0\\ 0 & -2 & 1\\ 0& 0& 5 \end{pmatrix} \] je ve schodovitém tvaru.
Věta (determinant matice ve schodovitém tvaru).
Determinant matice, která je ve schodovitém tvaru je roven součinu prvků v hlavní diagonále.
Totéž platí zejména pro matice diagonální, které mají nenulové prvky jenom v hlavní diagonále a tedy jsou ve schodovitém tvaru.
Příklad. Platí \[ \begin{vmatrix} 4& 7 &0\\ 0 & -2 & 1\\ 0& 0& 5 \end{vmatrix}=4\cdot (-2)\cdot 5=-40. \]
Souvislost některých pojmů
Pojmy lineární algebry spolu krásně souvisí.
Věta.
Buď \(A\) čtvercová matice řádu \(n\). Následující výroky jsou ekvivalentní:
- K matici \(A\) existuje matice inverzní \(A^{-1}\).
- Matice \(A\) je regulární, tj. \(\det A\neq 0\).
- Soustava lineárních rovnic \[AX=B\] má pro libovolnou pravou stranu \(B\) jediné řešení.
- Homogenní soustava lineárních rovnic \[AX=0\] má pouze nulové řešení.
- Každý vektor z \(\mathbb R^n\) lze vyjádřit jako lineární kombinaci vektorů tvořených řádky (sloupci) matice \(A\), a to jednoznačně, až na pořadí.
Například je-li \(\vec q\) vlastním vektorem matice \(A\) příslušným vlastní hodnotě \(\lambda\), platí \[A\vec q=\lambda \vec q.\] Odsud \[\begin{aligned}A\vec q-\lambda \vec q&=0\\ A\vec q-(\lambda I )\vec q &=0\\ (A-\lambda I )\vec q &=0\end{aligned}.\] Pokud chápeme poslední rovnost jako soustavu rovnic s koeficienty \((A-\lambda I)\), nulovou pravou stranou a nenulovým řešením \(\vec q\) (tj. bod 4 předchozí věty neplatí), musí být determinant matice \(A-\lambda I\) nulový (tj. bod 2 předchozí věty neplatí). Tím je motivována následující definice a dokázána následující věta.
Definice (charakteristická rovnice, charakteristický polynom).
Rovnice \[\det (A-\lambda I)=0\] s neznámou \(\lambda\) se nazývá charakteristická rovnice matice \(A\). Výraz na levé straně této rovnice je polynom proměnné \(\lambda\) a nazývá se charakteristický polynom matice \(A\).
Důsledek (vlastní čísla).
Vlastní čísla matice \(A\) jsou právě řešení charakteristické rovnice. Vlastní vektor \(\vec u\) příslušný vlastnímu číslu \(\lambda\) je nenulové řešení homogenní soustavy rovnic \[(A-\lambda I)\vec u=0.\]
Hookův zákon, matice tuhosti a poddajnosti
V minulé přednášce jsme odvodili tvar tenzoru malých deformací pro popis deformace tělesa ve tvaru \[\begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)\\ \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)& \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix}\]

Toto můžeme zapsat symbolicky \[\varepsilon_{ij}=\frac 12\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right).\tag{*}\] Pro deformaci v prostoru máme nikoliv dvě, ale tři souřadnice a tenzor deformací je tedy \(3\times 3\) symetrická matice, tj. matice, která má šest nezávislých komponent. (Zbylé tři komponenty dostaneme ze symetrie.) Tyto komponenty dostaneme postupnou volbou indexů ve vzorci (*) a můžeme je sestavit do sloupcového vektoru \[(\varepsilon_{11},\varepsilon_{22},\varepsilon_{33},\varepsilon_{23},\varepsilon_{13},\varepsilon_{12})^T\] Podobně, působící sílu můžeme rozdělit podle působení v jednotlivých směrech a tím dostaneme tenzor napětí, šest veličin charakterizujících napětí. (Zbylé tři jsou dány podmínkou, že se deformované těleso nepohybuje.) Pro další úvahy složky tenzoru napětí uspořádáme do sloupcového vektoru \[(\sigma_{11},\sigma_{22},\sigma_{33},\sigma_{23},\sigma_{13},\sigma_{12})^T.\]
Následující poučka je fyzikálně ověřený fakt, že vztah mezi složkami tenzoru napětí a tenzoru deformace je lineární. To nás nepřekvapí, protože z přednášek o derivacích na začátku semestru víme, že jakákoliv funkční závislost se dá linearizovat. Podstatné zde však je, že interval, na kterém má linearizace smysl, není příliš malý, tj. že tato linearizace platí pro prakticky významné případy.
Hookův zákon deformace (volná slovní formulace). Do určité hranice zatížení je libovolná složka tenzoru deformace úměrná libovolné složce tenzoru napětí.
K tomu si přidejme, že příspěvky k deformaci, způsobené různými složkami tenzoru napětí, se přirozeně sčítají. Matematicky vyjádřeno proto platí \[ \begin{pmatrix}\varepsilon_{11}\\\varepsilon_{22}\\\varepsilon_{33}\\\varepsilon_{23}\\\varepsilon_{13}\\\varepsilon_{12}\end{pmatrix} = S \begin{pmatrix}\sigma_{11}\\\sigma_{22}\\\sigma_{33}\\\sigma_{23}\\\sigma_{13}\\\sigma_{12}\end{pmatrix}, \] kde \(S\) je čtvercová \(6\times 6\) matice.

Fyzikální úvahy ukazují, že matice \(S\) je určitě symetrická a obsahuje celkem ne 36, ale jenom 21 nezávislých veličin. Nazývá se matice poddajnosti. V obecném případě tedy musíme pro popis deformace mít celkem 21 materiálových konstant. Tento počet se však výrazně redukuje, pokud je materiál například izotropní nebo ortotropní. Například ortotropní materiál jakým je dřevo, můžeme umístit do soustavy souřadnic tak, aby byl invariantní vůči symetrii podle jednotlivých průměten. Poté je možné odvodit, že nejobecnější možný tvar matice \(S\) je \[ S= \begin{pmatrix} S_{11} & S_{12} & S_{13} & 0 & 0 & 0 \\ S_{12} & S_{22} & S_{23} & 0 & 0 & 0 \\ S_{13} & S_{23} & S_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & S_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & S_{55} & 0\\ 0 & 0 & 0 & 0 & 0 & S_{66} \end{pmatrix},\] tj. tvar, obsahující jenom devět materiálových konstant. Odsud vidíme, že v takovém materiálu se smykové napětí projeví jenom na jedné komponentě tenzoru deformace, protože poslední tři sloupce, které udávají složky jednotlivých deformací způsobených napětími \(\sigma_{23}\), \(\sigma_{13}\) a \(\sigma_{12}\) mají jenom jednu nenulovou složku.
Pokud bychom použili k popisu obecnou soustavu souřadnic, nebylo by možné se na symetrii odvolávat. Matice \(S\) by obsahovala všechny prvky a bylo by nutné hledat bázi, v níž je její vyjádření nejjednodušší. U dřeva je však snadné rozpoznat význačné směry. Když soustavu souřadnic zvolíme tak, aby byla v souladu s těmito význačnými směry, docílíme tohot, že obdržíme matici \(S\) již přímo ve tvaru s co nejvíce nulami.
Někdy je vhodné umět určit napětí pomocí deformací. K tomu stačí Hookův zákon vynásobit maticí \(S^{-1}\) a obdržíme \[ \begin{pmatrix}\sigma_{11}\\\sigma_{22}\\\sigma_{33}\\\sigma_{23}\\\sigma_{13}\\\sigma_{12}\end{pmatrix}= S^{-1} \begin{pmatrix}\varepsilon_{11}\\\varepsilon_{22}\\\varepsilon_{33}\\\varepsilon_{23}\\\varepsilon_{13}\\\varepsilon_{12}\end{pmatrix}. \] Matice \(S^{-1}\) se nazývá matice tuhosti a označuje \(C\).
Souvislostí vlastních vektorů matice tuhosti a matice poddajnosti (nebo obecněji souvislostí vlastních vektorů matice a matice inverzní) se budeme zabývat na následujícím slidu.
Vlastní vektory matice a matice inverzní
Fyzikální úvaha snadno vede k závěru, že matice a matice inverzní mají stejné vlastní vektory. To proto, že pokud v některém směru je materiálová odezva násobkem podnětu, je i opačně podnět násobkem materiálové odezvy. To, že matice \(A\) a \(A^{-1}\) mají stejné vlastní vektory plyne i z toho, že pokud definiční vztah pro vlastní vektor matice \(A\), tj. vztah \[A\vec u=\lambda\vec u,\] vynásobíme zleva maticí \(\frac 1\lambda A^{-1}\), dostaneme vzhledem k identitě \(\frac 1\lambda A^{-1}A \vec u=\frac 1\lambda I \vec u =\frac 1\lambda \vec u\) rovnici \[\frac 1\lambda \vec u=A^{-1}\vec u,\] která vyjadřuje, že \(\vec u\) je vlastním vektorem matice \(A^{-1}\) s vlastním číslem \(\frac 1\lambda.\)
Shrnutí, hlavní myšlenky

- Přestože maticový součin nemá všechny vlastnosti na které jsme zvyklí u součinu čísel, jedna vlastnost zůstává: existence “převrácené hodnoty”. V případě matic je zobecnění převrácené hodnoty reprezentováno inverzní maticí.
- Pomocí matic je možné transformovat souřadnice bodů, vektorů a tenzorů z jedné soustavy souřadnic do jiné. Inverzní matice poté představuje zpětnou transformaci.
- Při transormaci tenzorů se snažíme o to, aby po transformaci byl tenzor co nejjednodušší. Pokud použijeme souřadnou soustavu s osami ve vlastních směrech (jsou kolmé a tedy je tato volba smysluplná), je tento tenzor je diagonální s vlastními čísly v diagonále.
- Pro identifikaci vlastních vektorů matice \(A\) je nutné řešit soustavu rovnic \[(A-\lambda I)v=0,\] ve které figuruje jistým i vlastní číslo \(\lambda\). Toto umožňuje definovat podmínku na vlastní čísla: uvažovaná soustava musí mít nenulové řešení.
- Existence nenulového řešení rovnice z předchozího bodu úzce souvisí s pojmem determinantu matice. Přesněji, aby soustava z předchozího bodu měla nenulové řešení, musí mít matice \(A-\lambda I\) nulový determinant.