V této přednášce se seznámíme s diferenciálními rovnicemi. To není nic jiného, než správný název pro to, čemu jsme dříve říkali matematické modely formulované pomocí derivace. Viděli jsme že tyto modely jsou v některých případech přirozeným matematickým aparátem pro popis reálně probíhajících dějů v přírodě. V přednášce se seznámíme se základním názvoslovím spojeným s touto problematikou, seznámíme se s metodami identifikace některých kvalitativních vlastností a u rovnic se separovanými proměnnými se naučíme hledat i analytické řešení. Protože se často setkáváme s modely nezávislými na čase, budeme se problematice těchto modelů věnovat podrobněji. Tyto modely mají tu vlastnost, že se ohraničená řešení po čase ustálí okolo stabilní hodnoty. Naučíme se hledat hodnoty odpovídající ustáleným řešením a z nich vybrat ty stabilní, k nimž systém může konvergovat, nebo nestabilní, které oddělují oblasti, ze kterých systém dospívá k jednotlivým stabilním stavům.

Motivace

Diferenciální rovnice jsou jakýmsi zlatým grálem modelování. V historii byly matematické modely založené na těchto rovnicích přímou motivací k rozvoji diferenicálního počtu (aby bylo možno tyto rovnice formulovat) a integrálního počtu (aby bylo možno tyto rovnice řešit). Od té doby dosáhla trojice derivace+integrál+diferenciální rovnice na obrovskou řadu úspěchů napříč mnoha obory.

• Odvození Keplerových zákonů pohybu planet matematickou cestou a tím potvrzení gravitačního zákona (Newton).
• Matematický aparát pro statické výpočty a výpočty nosníků (Euler, Bernoulli, Timoshenko).
• Objev planety Neptun předpovězením existence této planety na základě jinak nevysvětlitelných poruch v dráze planety Uran (Verrier).
• Teorie rovnováhy populací na ostrovech (MacArthur, Wilson).
• Teorie epidemií (Kermack, McKendrick).
• Chemické oscilátory (Prigogine), Nobelova cena za nerovnovážnou termodynamiku.
• Modely konkurence živočišných druhů, princip konkurenčního vyloučení (Gause).
• Modely predace živočišných druhů, oscilace v systému dravce a kořisti (Lotka, Volterra, Holling).
• Vysvětlení podstaty periodického přemnožování Choristoneura fumiferana v kanadských lesích (Ludwig, Jones, Holling).
• Systémová biologie, výzkum složitých interakcí mezi enzymy, geny a proteiny v živých organismech (Alon).
• Výzkum meteoritů s rodokmenem (Zdeněk Ceplecha, Pavel Spurný), výpočet jejich místa dopadu a místa, odkud meteorit přiletěl. Nesmírně cenný zdroj studijního materiálu.
• Zaměřovače pro řízení protiletecké obrany (Antonín Svoboda, český kybernetik). Svoboda později konstruoval výkonnější zaměřovače, získal prestižní vyznamenání námořnictva USA, jeho práce pomohla rozhodnout válku v tichomoří.

Někdy je nutné znát řešení rovnice, někdy stačí znát rovnici řídící studovaný proces a i bez znalosti řešení je možné získat užitečné informace.

• Chování řešení při změně rozměrů systému. Využívá se například v aerodynamických tunelech, kdy se rozměrné objekty testují na zmenšeninách. Dále se využívá tam, kde rovnici nedokážeme vyřešit, například model sesuvu hory do přehrady a následná tsunami v údolí Vajont nebo akustika v Janáčkově hudební síni.
• Náhrada jednoho problému jiným, který se chová stejně, ale je možné jej modelovat. Zahrnuje sestavování mechanických počítačů (zaměřovače prof. Svobody) nebo vodních počítačů (Moniac sestavený v roce 1949 pro model ekonomiky Nového Zélandu, vodní integrátor používaný Ruskem do 80-tých let)

Obyčejná diferenciální rovnice prvního řádu

Obyčejná diferenciální rovnice je rovnice, kde vystupuje neznámá funkce a její derivace. Setkáváme se s ní například všude tam, kde rychlost růstu nebo poklesu veličiny souvisí s její velikostí. Například rychlost s jakou se mění teplota horkého tělesa je funkcí teploty samotné. Rychlost tepelné výměny mezi dvěma tělesy je totiž úměrná rozdílu jejich teplot (Newtonův zákon). Takto se přirozeně diferenciální rovnice objevují v modelech nejrůznějších dějů jevů. Podstatu děje, který modelujeme, musí dodat fyzika, biologie nebo jiná aplikovaná věda. To v matematice obsaženo není. Matematika poté poslouží k analýze, jaké jsou pozorovatelné důsledky a tím se ověří, jestli příslušná aplikovaná věda správně vystihuje podstatu modelovaného děje.

Definice (diferenciální rovnice).

Obyčejnou diferenciální rovnicí prvního řádu rozřešenou vzhledem k derivaci (stručněji též diferenciální rovnicí, DR) s neznámou \(y\) rozumíme rovnici tvaru \[ \frac{\mathrm{d}y}{\mathrm{d}x}=\varphi(x,y) \tag{1}\] kde \(\varphi\) je funkce dvou proměnných.

(anglicky ordinary differential equation, ODE)

Další formy zápisu rovnice (1) jsou \[y'=\varphi(x,y),\] \[{\mathrm{d}y}=\varphi(x,y)\mathrm{d}x,\] \[{\mathrm{d}y}-\varphi(x,y)\mathrm{d}x=0.\]

Příklad. Najděte všechny funkce splňující \(y'=2xy\). (Naučíme se řešit později.)

Diferenciální rovnice bývá v aplikacích matematickým modelem kvantifikujícím scénář vývoje systému. Řešením jsou všechny možnosti, jak se tento systém může vyvjíjet. K jednoznačnému předpovězení budoucího stavu je ovšem nutno znát také stav počáteční, který ze všech teoreticky možných průběhů vybere průběh odpovídající modelované situaci. Tento stav vyjadřuje počáteční podmínka, uvedená v následující definici.

Definice (počáteční podmínka, Cauchyova úloha).

Nechť \(x_0\), \(y_0\) jsou reálná čísla. Úloha najít řešení rovnice
\[ \frac{\mathrm{d}y}{\mathrm{d}x}=\varphi(x,y), \tag{1}\] které splňuje zadanou počáteční podmínku \[ y(x_0)=y_0 \tag{2}\] se nazývá počáteční (též Cauchyova) úloha.

Řešení Cauchyovy úlohy nazýváme též partikulárním řešením rovnice. Graf libovolného partikulárního řešení se nazývá integrální křivka.

(anglicky initial condition, IC, initial value problem, IVP)

Příklad (praktická interpretace řešení počáteční úlohy).

• Pokud diferenciální rovnice udává rychlost ochlazování horkého nápoje a počáteční podmínka teplotu na počátku, je řešením počáteční úlohy funkce, do které dosadíme čas a přímo dostáváme teplotu nápoje v daném čase.
• Pokud diferenciální rovnice udává rychlost růstu populace živočišného druhu v čase a počáteční podmínka velikost populace na počátku sledování, je řešením počáteční úlohy funkce, do které dosadíme čas a přímo dostáváme velikost populace v daném čase.
• Pokud diferenciální rovnice udává rychlost nárůstu hladiny podzemní vody ve směru od čerpané studny a počáteční podmínka udává výšku hladiny ve studni, je řešením počáteční úlohy funkce udávající výšku hladiny podzemní vody jako funkci vzdálenosti od studny.

Příklad. Najděte všechny funkce splňující \(y'=2xy\) a \(y(0)=3\). (Naučíme se řešit později.)

Věta (existence a jednoznačnost řešení Cauchyovy úlohy).

Má-li funkce \(\varphi (x,y)\) ohraničenou parciální derivaci \(\frac{\partial \varphi}{\partial y}\) v okolí počáteční podmínky, potom má počáteční úloha (1)-(2) právě jedno řešení definované v nějakém okolí počáteční podmínky.

Příklad. Rovnice \[y'=y\tag{3}\] má řešení \(y=e^x\), což nahlédneme snadno, protože exponenciální funkce se nemění derivováním. Dosazením je možné ukázat, že má dokonce řešení \[y=Ce^x,\tag{4}\] kde \(C\) je libovolné číslo.

Příklad. Řešení počáteční úlohy \[y'=y, \quad y(x_0)=y_0\] najdeme tak, že využijeme řešení (4) a zařídíme, aby byla splněna počáteční podmínka. Tj. řešením počáteční úlohy je \[y= (y_0 e^{-x_0}) e^x.\] Vidíme, že toto řešení existuje pro každou počáteční podmínku a proto vzorec (4) popisuje dokonce všechna řešení rovnice (3).

Obecné a partikulární řešení

Řešení diferenciální rovnice je nekonečně mnoho. Zpravidla je dokážeme zapsat pomocí jediného vzorce, který obsahuje nějakou (alespoň do jisté míry libovolnou) konstantu \(C\). Takový vzorec se nazývá obecné řešení rovnice. Pokud není zadána počáteční podmínka a mluvíme o partikulárním řešení, máme tím na mysli jednu libovolnou funkci splňující diferenciální rovnici.

Příklad: Obecným řešením diferenciální rovnice \[y'=2xy\] je \[y=Ce^{x^2}, \quad C\in\mathbb{R}.\] Žádná jiná řešení neexistují, všechna řešení se dají zapsat v tomto tvaru pro nějakou vhodnou konstantu \(C\). Partikulárním řešením je například \(y=5e^{x^2}\). Řešením počáteční úlohy \[y'=2xy, \quad y(0)=3\] je \[y=3e^{x^2}.\]

Softwarové řešiče ODE (symbolicky):

• Wolfram Alpha
• Matlab
• Sage

Modely využívající diferenciální rovnice

Tepelná výměna

• Z fyziky víme, že rychlost tepelné výměny mezi dvěma tělesy je úměrná rozdílu jejich teplot (Newtonův zákon).
• Z přednášek o derivacích víme, že rychlost je matematicky derivace. Proces tepelné výměny probíhající podle Newtonova zákona je tedy možno modelovat diferenciální rovnicí \[ \frac{\mathrm dT}{\mathrm dt}=-k(T-T_0). \]
• Rovnice udává, že teplota \(T\) horkého tělesa se mění (rychlost změny je derivace) tak, že klesá (znaménko minus) rychlostí úměrnou (konstanta \(k\)) teplotnímu rozdílu mezi teplotou tělesa a teplotou okolí \(T_0\) (člen \(T-T_0\)).
• K rovnici v ideálním případě dodáváme materiálovou charakteristiku (konstantu úměrnosti \(k\)) a počáteční teplotu. Řešením rovnice je funkce udávající závislost teploty na čase. Chceme-li znát teplotu za určitý čas, není nutné provádět pokus a čekat na uplynutí požadované doby. Můžeme teplotu přímo vypočítat.
• Někdy může být vhodné nesledovat teplotu \(T\), ale rozdíl oproti okolní teplotě, \(\tau=T-T_0\). Rovnice se potom zjednoduší na \[ \frac{\mathrm d\tau}{\mathrm dt}=-k\tau,\] tedy na rovnici, kdy rychlost změny je úměrná funkční hodnotě.

Datování pomocí uhlíku

• Při datování archeologických nálezů pozůstatků živých organismů se využívá fyzikálního poznatku, že radioaktivní prvky se rozpadají rychlostí, která je úměrná množství dosud nerozpadnutého materiálu.
• Rychlost, s jakou se mění množství (a tedy i koncentrace \(y\) v daném vzorku) nerozpadnutého radioaktivního materiálu je tedy matematicky popsána rovnicí \[\frac{\mathrm dy}{\mathrm dt}=-\lambda y,\] kde \(\lambda\) je konstanta úměrnosti. Tato rovnice je přirozeným důsledkem toho, že pro daný nestabilní izotop mají všechny atomy stejnou pravděpodobnost, že u nich dojde k rozpadu a tato pravděpodobnost se s časem nemění.
• Vhodný radioaktivní prvek vybereme podle toho, jak starý vzorek chceme datovat. Nejčastěji měříme množství radioaktivního uhlíku \(^{14}C\) vztažené k množství stabilního \(^{12}C\). Počáteční podmínka je známa (předpokládáme stejný poměr zastoupení jako relativně nedávno, před průmyslovou revolucí) a díky tomu můžeme najít funkci udávající, jak s časem klesá zastoupení radioaktivního uhlíku. Obsah radioaktivního i stabilního uhlíku je možné změřit a tím získáme odhad, kolik procent radioaktivního uhlíku se rozpadlo. Řešení počáteční úlohy poté použijeme pro odhad doby, kdy organismus přestal spotřebovávat uhlík z atmosféry, tj. odhad stáří vzorku.
• Při pokusu o datování kostí dinosaurů klesne množství radioaktivního uhlíku pod měřitelnou úroveň. Proto se v tomto případě používají látky s delším poločasem rozpadu.

Vývoj populace a její ekologický lov

• Zkoumejme velikost \(y\) určité populace, v prostředí s nosnou kapacitou \(K\).
• Budeme pracovat s pojmem specifická míru růstu populace, což je rychlost růstu populace vztažená na jednotkové množství populace. Realistickým předpokladem dodaným biologickými vědami je, že v prostředí s omezenými úživnými vlastnostmi specifická míru růstu populace klesá s tím, jak se velikost populace přibližuje k nosné kapacitě, a specifická rychlost růstu populace je modelována funkcí \(r\left(1-\frac yK\right)\). Podle velkosti koeficientů v této rovnici dělíme živočichy na r-stratégy a K-stratégy a toto dělení odráží, jak se snaží druh vyrovnávat se změnami prostředí.
• Za uvedených předpokladů je možno vývoj populace popsat rovnicí \[\frac 1y \frac{\mathrm dy}{\mathrm dt}=r\left(1-\frac yK\right),\] tj. \[\frac{\mathrm dy}{\mathrm dt}=ry\left(1-\frac yK\right).\] Tato rovnice se nazývá logistická rovnice.
• Pokud lovem snížíme přírůstky populace, můžeme tento proces modelovat rovnicí \[\frac{\mathrm dy}{\mathrm dt}=ry\left(1-\frac yK\right)-h(y),\] kde \(h(y)\) je intenzita lovu populace o velikosti \(y\). Modelování tohoto procesu umožní nalezení ekonomicky výhodné ale přitom trvale udržitelné strategie lovu.

Lovci meteoritů z ČSSR a ČR

Česká republika je na světové špičce ve oblasti propočítávání dráhy meteoritů ze světelné stopy zachycené sítí bolidových kamer. Vědcům z Astronomického ústavu se podařilo

• jako prvním na světě najít pozůstatky meteoritu propočítáním jeho dráhy ze snímků zachycených speciálními kamerami a zpětně propočítat, odkud meteorit přiletěl (meteorit Příbram, 1959, první “meteorit s rodokmenem”, tj. s doloženým původem),
• jako prvním na světě najít pozůstatky meteoritu 20 let po dopadu použitím analýz, které v době dopadu meteoritu nebyly k dispozici (meteorit Benešov, dopad 1991, nalezen 2011),
• propočítat a najít (mimo jiné i na dně jezera!) zbytky meteoritu Čeljabinsk z roku 2013.

Meteority s vystopovaným původem jsou extrémně vzácné (do roku 2000 jenom 5 meteoritů, do roku 2016 pouze 31 meteoritů) a tým založený Zdeňkem Ceplechou a nyní vedený Pavlem Spurným se podílel na výpočtu drah většiny z nich. Použité metody jsou popsány například v článku Ceplecha, Revelle: Fragmentation model of meteoroid motion, mass loss, and radiation in the atmosphere, Meteoritics & Planetary Science 40, Nr 1, 35–54 (2005). Například ztráta rychlosti třením v atmosféře je modelována rovnicí \[\frac{\mathrm dv}{\mathrm dt}=-K\rho m^{-1/3}v^{2}\] a ztráta hmotnosti vypařováním \[\frac{\mathrm dm}{\mathrm dt}=-K\sigma \rho m^{2/3}v^3.\] Jedná se o diferenciální rovnice, kde zrychlení (derivace rychlosti) a časová změna hmotnosti (derivace hmotnosti podle času, rychlost, s jakou ubývá hmotnost) je úměrná vhodným mocninám těchto veličin.

Testová otázka

Geometrická interpretace a transformace jednotek

Geometrická interpretace ODE

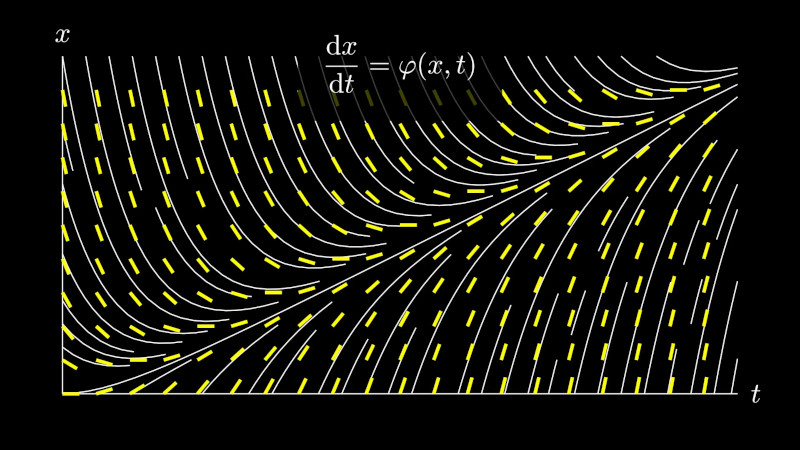
Protože derivace funkce v bodě udává směrnici tečny ke grafu funkce v tomto bodě, lze rovnici \[\frac{\mathrm dy}{\mathrm dx}=\varphi(x,y)\tag{1}\] chápat jako předpis, který každému bodu v rovině přiřadí směrnici tečny k integrální křivce, která tímto bodem prochází. Sestrojíme-li v dostatečném počtu (například i náhodně zvolených) bodů \([x,y]\) v rovině vektory \((1,\varphi(x,y))\), obdržíme směrové pole diferenciální rovnice — systém lineárních elementů, které jsou tečné k integrálním křivkám.

Počáteční podmínka \(y(x_0)=y_0\) geometricky vyjadřuje skutečnost, že graf příslušného řešení prochází v rovině bodem \([x_0,y_0]\). Má-li tato počáteční úloha jediné řešení, neprochází bodem \([x_0,y_0]\) žádná další křivka. Má-li každá počáteční úloha jediné řešení (což bude pro nás velice častý případ), znamená to, že integrální křivky se nikde neprotínají.

Transformace diferenciální rovnice

Naučíme se vyjadřovat diferenciální rovnici v jiných proměnných tak, aby bylo možné snížit počet parametrů v této rovnici. Pro jednoduchost budeme uvažovat jenom případ, kdy nová proměnný je lineární funkcí původní proměnné.

Uvažujme funkci \(y\) proměnné \(x\). Připomeneme si vzorce pro derivaci součtu, derivaci konstantního násobku a derivaci složené funkce, ale uvedeme si je v kontextu vhodném pro studium diferenciálních rovnic.

• Z derivace součtu a z derivace konstanty plyne pro funkci \(y\) a konstantu \(y_0\) vztah \[ \frac{\mathrm d (y\pm y_0)}{\mathrm dx} = \frac{\mathrm d y}{\mathrm dx} \pm \frac{\mathrm d y_0}{\mathrm dx} = \frac{\mathrm d y}{\mathrm dx} \pm 0= \frac{\mathrm d y}{\mathrm dx}.\]
• Z derivace konstantního násobku funkce plyne pro funkci \(y\) a konstantu \(k\) vztah \[ \frac{\mathrm d (ky)}{\mathrm dx} = k\frac{\mathrm d y}{\mathrm dx}.\]
• Z derivace složené funkce plyne pro konstantu \(k\) a veličinu \(X = kx\) vztah \[ \frac{\mathrm d y}{\mathrm d x} = \frac{\mathrm d y}{\mathrm dX} \frac{\mathrm d X}{\mathrm dx} = \frac{\mathrm d y}{\mathrm d X} k \] tj. \[ \frac{\mathrm d y}{\mathrm d (kx)} = \frac{\mathrm d y}{\mathrm d X} = \frac 1k \frac{\mathrm d y}{\mathrm d x}.\]

Výše uvedené výpočty je možno shrnout do pravidla v následující poznámce.

Poznámka (transformace diferenciální rovnice do jiných jednotek).

Pro \(Y=k_1(y-y_0)\) a \(X=k_2 x\) platí \[ \frac{\mathrm d Y}{\mathrm d X} = \frac{\mathrm d \Bigl(k_1(y-y_0)\Bigr)}{\mathrm d (k_2 x)} = \frac{k_1}{k_2} \frac{\mathrm dy}{\mathrm dx}\] a podobně (všimněte si druhé mocniny u \(k_2\) díky druhé derivaci) \[ \frac{\mathrm d^2 Y}{\mathrm d X^2} = \frac{k_1}{k_2^2} \frac{\mathrm d^2y}{\mathrm dx^2}.\] Výraz nalevo neobsahuje konstanty, které jsou ve výrazu napravo. Tyto konstanty jsou v definici nových veličin \(X\) a \(Y\).

Navíc vzorec z poznámky silně připomíná klasické počítání se zlomky. Proto máme Leibnizův tvar zápisu derivací \(\frac{\mathrm dy}{\mathrm dx}\) při studiu diferenciálních rovnic více v oblibě, než zápis Lagrangeův, \(y'\).

Příklad. Diferenciální rovnice tepelné výměny \[\frac{\mathrm dT}{\mathrm dt}=-k(T-T_\infty), \quad T(0)=T_0\tag{*}\] obsahuje tři parametry: teplotu okolního prostředí \(T_\infty\), počáteční teplotu \(T_0\) a konstantu \(k\) související s fyzikálními vlastnostmi prostředí. Postupně můžeme posunout teplotní stupnici tak, aby teplota okolí byla nula a počáteční teplota jedna, tj. hodnotu \(T\) snížíme o \(T_\infty\) a upravíme dílek stupnice \((T_0-T_\infty)\)-krát \[\frac{\mathrm d\left(\frac{T-T_\infty}{T_0-T_\infty}\right)}{\mathrm dt}=-k\frac{T-T_\infty}{T_0-T_\infty}\] vydělit konstantou \(k\) \[\frac{\mathrm d\left(\frac{T-T_\infty}{T_0-T_\infty}\right)}{k\mathrm dt}=-\frac{T-T_\infty}{T_0-T_\infty}\] a přeškálovat pomocí konstanty \(k\) čas \[\frac{\mathrm d\left(\frac{T-T_\infty}{T_0-T_\infty}\right)}{\mathrm d(kt)}=-\frac{T-T_\infty}{T_0-T_\infty}.\] Po substituci \(y=\frac{T-T_\infty}{T_0-T_\infty}\), \(x=kt\) má úloha tvar \[\frac{\mathrm d y}{\mathrm d x}=-y,\quad y(0)=1. \tag{**}\] Nová rovnice (**) neobsahuje žádné parametry a proto je pro studium jednodušší. Přesto je v ní obsažena veškerá informace obsažená v rovnici (*). Tuto informaci je však nutno interpretovat v kontextu definice nových proměnných. Například to, že všechna řešení rovnice (**) konvergují k nule znamená, že všechna řešení rovnice (*) konvergují k \(T_0\). To, že řešení rovnice (**) klesne na poloviční hodnotu za čas \(\ln 2\) znamená, že vzdálenost řešení rovnice (*) od rovnovážného stavu se na polovinu zmenší za čas \(\frac 1k \ln 2\).

Poznámka (nondimenzionalizace, rozměrová analýza).

Proces eliminace parametrů z modelu popsaného diferenciální rovnicí se nazývá nondimenzionalizace nebo rozměrová analýza modelu, protože eliminaci parametrů je vhodné provádět tak, aby výsledné nové veličiny vycházely bez fyzikálních jednotek. K tomu se provádí rozbor jednotek jednotlivých veličin. V jednoduchých případech však stačí primitivní postup popsaný v odstavcích výše a ukázaný na příkladu. V tomto příkladě veličina \(x\) nemá fyzikální jednotku, protože je součinem konstanty \(k\) (s jednotkou \(\mathrm s^{-1}\)) a času \(t\) (s jednotkou \(\mathrm s\)). Je možné ji považovat za bezrozměrný čas. Veličina \(y\) také nemá fyzikální jednotku, protože je podílem dvou teplot a je možné ji považovat za bezrozměrnou teplotu.

V úloze s ochlazováním tělesa bylo zavedení nových veličin přirozené. I u méně zřejmých úloh zkušenosti ukazují, že je vhodné volit transformaci tak, aby vznikly veličiny bezrozměrné, které nemají fyzikální jednotku. Například v Horáček, Fyzikální a mechanické vlastnosti dřeva I je zavedena bezrozměrná vlhkost, bezrozměrný čas a bezrozměrná vzdálenost na straně 61 pro rovnici popisující difuzi a charakteristická délka, Biotovo číslo (bezrozměrná tepelná vodivost) a bezrozměrná teplota, bezrozměrný čas a bezrozměrná vzdálenost pro rovnici popisující vedení tepla na stranách 88 a 89.

Obecné výhody transformace diferenciálních rovnic jsou následující.

• Po transformaci obsahuje rovnice v nových veličinách menší množství parametrů.
• Nové veličiny jsou bez fyzikální jednotky a tudíž vhodné pro numerické simulace, kdy se zpravidla o jednotky nestaráme.
• Nové veličiny zpravidla nabývají hodnot řádově srovnatelných s jedničkou. Nejedná se ani o tisíce ani o tisíciny.

Všechny tři uvedené skutečnosti vedou k tomu, že s transformovanými rovnicemi se lépe pracuje v numerických modelech.

Příklad. Diferenciální rovnici logistického růstu s lovem konstantní intenzity \[\frac{\mathrm dx}{\mathrm dt}=rx\left(1-\frac xK\right)-h\] je možno přepsat do tvaru \[\frac{\mathrm d\frac xK}{\mathrm d(rt)}=\frac xK\left(1-\frac xK\right)-\frac{h}{rK}\] a po zavedení bezrozměrné velikosti populace \(X=\frac xK\), bezrozměrného času \(T=rt\) a bezrozměrné intenzity lovu \(H=\frac{h}{rK}\) má model tvar \[\frac{\mathrm dX}{\mathrm dT}=X\left(1-X\right)-H.\] Jinými slovy, chování modelu například z hlediska konvergence řešení k nenulové hodnotě závisí na parametru \(\frac{h}{rK}.\) Pokud se sníží nosná kapacita prostředí o dvacet procent, je nutné pro udržení stejného chování rovnice snížit lov nebo zvýšit koeficient \(r\) tak, aby poměr \(\frac{h}{rK}\) zůstal zachován.

ODE tvaru \(\frac{\mathrm dy}{\mathrm dx}=f(y)\), autonomní ODE

Rovnice \[\frac{\mathrm dy}{\mathrm dx}=f(y)\tag{♣}\] se nazývá autonomní, nebo též nezávislá na čase. Je speciálním případem rovnice se separovanými proměnnými, která je uvedena na dalším slidu a naučíme se ji řešit analytickou cestou. Proto se nyní nebudeme zaměřovat na hledání obecného řešení, ale pokusíme se popsat chování řešení, aniž bychom tato řešení znali. Pokusíme se s co nejmenší námahou říct, jak se budou řešení chovat.

• Je-li \(f(y_0)=0\), je konstantní funkce \(y(x)=y_0\) řešením rovnice (♣). Protože derivace konstantní funkce je nula, vidíme, že řešením rovnice \[f(y)=0\] obdržíme všechna konstantní řešení rovnice (♣). Tato konstantní řešení se nazývají stacionární body.
• Stacionární body a jim odpovídající konstantní řešení představují rovnovážný stav. Často nás zajímá, jestli při vychýlení z tohoto rovnovážného stavu má systém tendenci se vrátit do původního stavu, nebo se od původního stavu dále odchylovat.
  
• Pokud se při malém vychýlení z rovnovážného stavu systém do tohoto stavu vrací, mluvíme o stabilním stacionárním bodu.
• Pokud se systém po malé výchylce do tohoto rovnovážného stavu nevrací, ale vyvíjí se k dalšímu stacionárnímu bodu nebo neohraničeně, mluvíme o nestabilním stacionárním bodu.

Následující věta umožní odlišit stabilní a nestabilní stacionární body. Protože v přírodě dochází k drobným perturbacím neustále, udává vlastně, které stacionární stavy jsou realizovatelné a můžeme je v přírodě pozorovat a které jsou prakticky nerealizovatelné.

Věta (stabilita konstantních řešení).

Jestliže platí \(f(y_0)=0\), je konstantní funkce \(y(x)=y_0\) konstantním řešením rovnice \[\frac{\mathrm dy}{\mathrm dx}=f(y).\] Toto řešení je stabilní pokud \(\frac{\mathrm df}{\mathrm dy}(y_0)<0\) a nestabilní pokud \(\frac{\mathrm df}{\mathrm dy}(y_0)>0\).

Pro grafickou intepretaci je vhodné připomenout, že funkce s kladnou derivací jsou rostoucí a funkce se zápornou derivací klesající. Pokud má tedy pravá strana derivaci různou od nuly, poznáme stabilitu z monotonie pravé strany.

Příklad. Logistická diferenciální rovnice s konstantním lovem \(h\), tj. rovnice \[\frac{\mathrm dy}{\mathrm dt}=ry\left(1-\frac yK\right)-h,\] má pro malé \(h\) dva stacionární body. Funkce \(ry\left(1-\frac yK\right)\) je parabola otočená vrcholem nahoru a s nulovými body \(y=0\) a \(y=K\). V prvním stacionárním bodě je funkce rostoucí a tento stacionární bod je nestabilní. Ve druhém stacionárním bodě je funkce klesající a tento stacionární bod je stabilní. Jak se zvyšuje faktor \(h\), graf paraboly se posouvá směrem dolů a oba stacionární body se posouvají směrem k sobě a k  vrcholu. Jejich stabilita zůstává neporušena. To znamená, že sice pořád existuje stabilní stav, ale se zvyšující se intenzitou lovu se tento stacionární stav dostává stále blíže ke stavu nestacionárnímu a rovnováha je tedy poněkud křehká.

Poznámka (autonomní rovnice s rozdílem na pravé straně).

Rovnice \[\frac{\mathrm dy}{\mathrm dx}=g(y)-h(y)\] má stacionární bod \(y_0\), jestliže \[g(y_0)=h(y_0).\] Často jsou funkce \(g\) a \(h\) zadány graficky a stacionární bod je v průsečíku grafů funkcí \(g\) a \(h\). Ze vzájemné polohy těchto grafů také vidíme, zda je stacionární bod stabilní (funkce \(g\) je napravo od bodu \(y_0\) pod funkcí \(h\) a nalevo nad ní) nebo nestabilní (naopak).

Příklad. Teplotní bilanci Země je možno vyjádřit rovnicí \[\frac{\mathrm dT}{\mathrm dt}=R_{\text{in}}(T)-R_{\text{out}}(T),\] kde \(R_{\text{in}}\) a \(R_{\text{out}}\) jsou funkce dané na obrázku. Vidíme tři průsečíky, tj. tři stacionární body. Uvažujme stacionární bod nejvíce napravo. Malá výchylka nahoru k větší teplotě nás posune do oblasti, kde převažuje vyzařování energie, \(R_{\text{out}}\) je vetší než \(R_{\text{in}}\), pravá strana je záporná a teplota klesá zpět do stacionárního stavu. Podobně, malá výchylka směrem dolů způsobí nárůst a opět návrat do stacionárního stavu. Stacionární stav zcela vpravo je tedy stabilní. Podobně ukážeme, že stacionární stav odpovídající průsečíku zcela vlevo je také stabilní. Naopak, stacionární stav uprostřed je nestabilní, libovolná výchylka z tohoto stavu způsobí přechod systému do některého ze stabilních stavů.

Testová otázka Testová otázka Testová otázka Testová otázka

ODE tvaru \(\frac{\mathrm dy}{\mathrm dx}=f(x)g(y)\) (rovnice se separovanými proměnnými)

Definice (ODE se separovanými proměnnými).

Diferenciální rovnice tvaru \[ \frac{\mathrm dy}{\mathrm dx}=f(x)g(y) \tag{S}\] kde \(f\) a \(g\) jsou funkce spojité na (nějakých) otevřených intervalech se nazývá obyčejná diferenciální rovnice se separovanými proměnnými.

Příklad: Rovnice \[y'+xy +xy^2=0\] je rovnicí se separovanými proměnnými, protože je možno ji zapsat ve tvaru \[y'=-xy(y+1).\] Rovnice \[y'=x^2-y^2\] není rovnice se separovatelnými proměnnými.

Řešení ODE se separovanými proměnnými

1. Má-li algebraická rovnice \(g(y)=0\) řešení \(k_1\), \(k_2\), …, \(k_n\), jsou konstantní funkce \(y\equiv k_1\), \(y\equiv k_2\), …, \(y\equiv k_n\) řešeními rovnice.

2. Pracujme na intervalech, kde \(g(y)\neq 0\) a odseparujeme proměnné. \[ \frac{\mathrm{d}y}{g(y)}=f(x)\mathrm{d}x\]

3. Získanou rovnost integrujeme. Tím získáme obecné řešení v implicitním tvaru. \[ \int \frac{\mathrm{d}y}{g(y)}=\int f(x)\mathrm{d}x+C\]

4. Pokud je zadána počáteční podmínka, je možné ji na tomto místě dosadit do obecného řešení a určit hodnotu konstanty \(C\). Tuto hodnotu poté dosadíme zpět do obecného řešení a obdržíme řešení partikulární.

5. Pokud je to možné, převedeme řešení (obecné nebo partikulární) do explicitního tvaru (vyjádříme odsud \(y\)).

Poslední krok (převod do explicitního tvaru) je volitelný, zpravidla záleží na tom, co dalšího hodláme s řešením dělat. Pro většinu výpočtů je však explicitní tvar vhodnější než tvar implicitní a proto se o něj vždy snažíme.

Poznámka (zápis partikulárního řešení pomocí určitého integrálu).

V případě počáteční podmínky \(y(x_0) = y_0\) je možné spojit třetí a čtvrtý krok a použít určitý integrál \[ \int_{y_0}^y \frac{\mathrm{d}t}{g(t)}=\int_{x_0}^x f(t)\mathrm{d}t. \]

Počáteční úloha má jediné řešení, pokud má pravá strana ohraničenou parciální derivace podle \(y\), jak je zmíněno v úvodu přednášky. Nicméně pro diferenciální rovnici se separovanými proměnnými je možné vyslovit následující mnohem jednodušší postačující podmínku pro jednoznačnost řešení.

Věta (existence a jednoznačnost řešení Cauchyovy úlohy pro rovnici se separovanými proměnnými).

Je-li \(g(y_0)\neq 0\), má počáteční úloha \[\frac{\mathrm dy}{\mathrm dx}=f(x)g(y),\qquad y(x_0)=y_0\] právě jedno řešení definované v nějakém okolí počáteční podmínky.

Diferenciální rovnice růstu vodní kapky

Modelujme růst kulové kapky. Ta roste tak, že na povrchu kondenzují vodní páry. Kapka proto roste tak, že její objem se zvětšuje rychlostí úměrnou povrchu. Povrch je zase úměrný druhé mocnině poloměru a poloměr je úměrný třetí odmocnině objemu. Platí tedy (po sloučení všech konstant úměrnosti do jedné) \[\frac{\mathrm dV}{\mathrm dt}=kV^{2/3}.\]
Tato rovnice má konstantní řešení \(V=0\). Nekonstantní řešení dostaneme po úpravě \[V^{-2/3}\mathrm dV=k\mathrm dt\] a po integraci \[\int V^{-2/3}\mathrm dV=k\int \mathrm dt,\] což dává \[3V^{1/3}=kt+C\] a \[V=\left(\frac 13 kt+ \frac 13 C\right)^3,\] tj. \[V=\left(k_0t+ c\right)^3,\] kde \(k_0=\frac 13 k\) a \(c=\frac 13 C\) jsou konstanta spojená rychlostí kondenzace a integrační konstanta.

Všimněte si, že počáteční úloha s počáteční podmínkou \(V(0)=0\) má konstantní nulové řešení \[V(t)=0\] a nenulové řešení \[V(t)=(k_0t)^3.\] Máme zde tedy nejednoznačnost v řešení počáteční úlohy. Tato nejednoznačnost není v rozporu s větou o existenci a jednoznačnosti řešení, protože pravá strana je nulová (podmínka pro separovatelnou rovnici není splněna) a nemá ohraničenou derivaci podle \(V\) (podmínka pro obecnou rovnici také není splněna). A nejednoznačnost má v tomto případě dokonce fyzikální význam. Plynné skupenství může existovat i pod bodem kondenzace. Takovému jevu se říká přechlazená pára. Aby došlo ke kondenzaci, musí být k dispozici kondenzační jádra, například nečistoty ve vzduchu. Proto ve znečištěném ovzduší dochází častěji ke kondenzaci a tvorbě mlhy. Své by o tom mohli vyprávět obyvatelé Londýna, kteří se proslulých mlh zbavili poté, co se omezilo topení uhlím. My dnes spíše známe přechlazenou tekutinu ve formě hřejících polštářků, kde se po lupnutí plíškem spustí přeměna skupenství na pevné spojená s intenzivním uvolněním tepla.

Diferenciální rovnice vyšších řádů

Shrnutí, hlavní myšlenky

• Aplikované vědy (fyzika, biologie, nauka o materiálu, hydrologie) přirozeně formulují své zákony a poznatky mimo jiné i kvantitativně a pomocí pojmů vyjadřujících rychlosti změn. Při přepisu těchto zákonitostí do matematických modelů používáme derivaci jako rychlost růstu (případně záporně vzatou derivaci, jako rychlost poklesu).
• Pokud známým způsobem souvisí změna veličiny popisující stav systému s velikostí této veličiny, je příslušným matematickým modelem diferenciální rovnice. S tímto jsme se setkali již mnohokrát ve cvičení během semestru.
• Naučili jsme se základní diferenciální rovnice řešit analyticky, řekli jsme si, že se dají řešit numericky (v praxi využijeme předpřipravené procedury a proto se touto problematikou nemusíme zabývat do hloubky) a naučili jsme se i rovnice transformovat do jiných proměnných, které mohou být pro studium problému přínosnější, než původní veličiny.