Derivace funkce
Robert Mařík
2020,2021, 2022
Motivace.
- Seznámíme se s pojmem derivace funkce. Tento pojem umožňuje u měnící se veličiny určovat, jak rychle se tato veličina mění. Zatímco v případě rovnoměrné změny je problematika rychlosti triviální a řešitelná středoškolskými prostředky, v případě změny jejíž rychlost akceleruje nebo klesá je nutné zapojit zcela nový aparát, nazývaný infinitezimální počet. Derivace je jeho prvním představitelem. S dalším, integrálem, se setkáme později.
- Ze střední školy je student zvyklý na to, že si má osvojit dovednosti, jak se to počítá. Pro nás je však už důležité si uvědomit, že vůbec nějak dokážeme zachytit rychlost změny. Že s tím dokážeme pracovat, že například dokážeme pomocí těchto pojmů naformulovat fyzikální zákony pracující s rychlostmi změn. A věřte či ne, takové jsou skoro všechny. V podstatě celá středoškolská fyzika je postavena na studiu veličin, měnících se konstantní rychlostí. S tím se dá modelovat mnoho dějů okolo nás, ale pro hlubší poznání světa je to žalostně málo. Derivace umožní pracovat s libovolnými rychlostmi změn. Nesoustřeďte se proto na počítání, soustřeďte se na význam a využití. Soustřeďte se na rozpoznání kontextu, ve kterém problematiku studujeme.
- Po přečtení přednášky byste měli mít v hlavě vybudovanou spojnici mezi derivací a rychlostí. Pokud se ve slovním popisu děje mluví o rychlosti, v matematickém modelu tato rychlost figuruje prostřednictvím derivace.
Funkce

Při hlubším než povrchním studiu libovolného systému nás zajímají veličiny spojené se studovaným problémem a vztahy mezi těmito veličinami. Tyto vztahy jsou zprostředkovávány funkcemi. Jako příklad si představme nosník vetknutý do země a na konci zatížený vodorovnou silou \(F\). Deformace nosníku \(\delta\) na konci (skalární veličina) souvisí s velikostí zatěžující síly (skalární veličina). Pro studium problému je vhodné mít převodní pravidlo, které pro každé zatížení udává deformaci. Toto pravidlo bude z matematického úhlu pohledu funkce (funkce jedné proměnné). Může mít například formu \[\delta=\frac 1k F,\] kde \(k\) je konstanta pro daný nosník (tuhost).
Na řadu použití stačí intuitivní chápání funkce i jejích vlastností. Někdy je však potřeba si myšlenky zpřesnit a plně formalizovat. V následujícím představíme definici funkce, rozdělíme funkce na rostoucí, klesající a ostatní a ukážeme si využití těchto vlastností.
Funkce jedné proměnné
Definice (funkce jedné proměnné).
Buďte \(A\) a \(B\) neprázdné podmnožiny množiny reálných čísel. Pravidlo \(f\), které každému prvku množiny \(A\) přiřadí jediný prvek množiny \(B\) se nazývá funkce (přesněji: reálná funkce jedné reálné proměnné). Zapisujeme \(f:A\to B\). Skutečnost, že prvku \(a\in A\) je přiřazen prvek \(b\in B\) zapisujeme \(f(a)=b\). Přitom říkáme, že \(b\) je obrazem prvku \(a\) při zobrazení \(f\), resp. že \(a\) je vzorem prvku \(b\) při zobrazení \(f\).
Poznámka (terminologie).
Množina \(A\) z definice funkce se nazývá definiční obor funkce \(f\). Označujeme \(\mathrm D(f)\) (resp. \(\mathrm{Dom}(f)\)). Je-li \(M\) podmnožina definičního oboru, definujeme množinu \(f(M)\) jako množinu všech obrazů bodů množiny \(M\). Množina \(f(\mathrm{Dom}(f))=b\) se nazývá obor hodnot funkce \(f\). Označujeme \(\mathrm H(f)\) (resp. \(\mathrm{Im}(f)\)).
Je-li \(y=f(x)\) nazýváme proměnnou \(x\) též nezávislou proměnnou a proměnnou \(y\) závislou proměnnou. Grafem funkce rozumíme množinu všech uspořádaných dvojic \([x,y]\in\mathbb R^2\) s vlastností \(y=f(x)\).
Přímá a nepřímá úměrnost
Je to až k nevíře, ale k popisu obrovského množství dějů stačí čtyři základní operace: sčítání, odčítání, násobení a dělení. Vzhledem k požadavku na konzistenci fyzikálních jednotek se nejčastěji setkáváme s násobením a dělením a proto funkce pracující s těmito operacemi mají výsadní postavení. Takový, že si vysloužily pojmenování běžně užívané i mezi nematematiky: přímá a nepřímá úměrnost. Je to formální popis situace, kdy souvislost mezi dvěma veličinami je zprostředkována násobením konstantou (přímá úměrnost), nebo kdy je násobením konstantou zprostředkována souvislost mezi jednou veličinou a převrácenou hodnotou druhé veličiny.
Definice (přímá a nepřímá úměrnost).
Veličina \(y\) je přímo úměrná veličině \(x\) jestliže existuje konstanta \(k\) taková, že platí \[y=kx.\] Veličina \(y\) je nepřímo úměrná veličině \(x\) jestliže existuje konstanta \(k\) taková, že platí \[y=\frac kx.\]
Poznámka. Je-li veličina \(y\) úměrná veličině \(x\), píšeme \[y\sim x\text{ nebo }y\propto x.\] Je-li navíc konstanta úměrnosti blízká jedničce, tj. \(x\) a \(y\) jsou blízké, píšeme \[y\approx x.\] Pro nepřímou úměrnost píšeme podobně \(y\sim \frac 1x\), \(y\propto \frac 1x\) a \(y\approx \frac 1x\) s využitím toho, že nepřímá úměrnost je vlastně přímá úměrnost pro převrácenou hodnotu.

Příklad.
- Při pohybu konstantní rychlostí je dráha \(s\) úměrná času \(t\). Příslušnou konstantou úměrnosti je rychlost \(v\), tj. \(s=vt\). Pro \(t=1\) je dráha \(s\) přímo rovna konstantě úměrnosti \(v\). Proto můžeme konstantu úměrnosti reprezentovat jako dráhu za jednotku času. Takto rychlost i chápeme a v tomto smyslu čteme i její jednotku. Nečteme “kilometrů lomeno hodin” ale “kilometrů za hodinu”.
- Při pohybu po předem stanovené dráze \(s\) je čas nepřímo úměrný rychlosti \(v\). Platí \(t=\frac sv\). Konstantou úměrnosti je dráha \(s\). Pro \(v=1\) je čas přímo roven dráze. Proto je možno konstantu úměrnosti slovně vyjádřit tak, že udává čas, který je nutný pro projetí příslušné dráhy jednotkovou rychlostí.
- Při periodickém pohybu je frekvence \(f\) nepřímo úměrná periodě \(T\). Příslušnou konstantou úměrnosti je jednička, tj. \(f=\frac 1T\).
- Objem \(V\) koule o poloměru \(r\) je přímo úměrný třetí mocnině poloměru. Existuje tedy konstanta \(k\) taková, že platí \(V=k r^3\). Pro \(r=1\) je objem \(V\) přímo roven konstantě \(k\). Konstanta proto \(k\) vyjadřuje objem koule jednotkového poloměru. Protože objem koule jednotkového poloměru je \(\frac 43 \pi\) učí se žáci v matematice rovnou vzorec \(V=\frac 43 \pi r^3\).
- Dynamická odezva stromů ve větru je častým námětem mnoha vědeckých prací. Souhrnná studie Jackson, T. et al (2021) The motion of trees in the wind: a data synthesis. Biogeosciences. tvrdí, že v některých případech (zpravidla listnáče v lese) je základní frekvence vlastních kmitů stromů nepřímo úměrná odmocnině výšky, což je vztah známý pro kyvadlo. \[f=\frac 1T \sim \frac 1{\sqrt H}.\] U jiných stromů (zpravidla jehličnaté stromy) je základní frekvence přímo úměrná průměru \(d\) a nepřímo úměrná druhé mocnině výšky \(H\), tj. \[f=\frac 1T\sim \frac{d}{H^2}.\] Tento vztah je znám pro nosníky. To ukazuje, že pro některé stromy je pro dynamické vlastnosti dominantní hmota v koruně, pro jiné stromy hmota podél kmene.
- Síla působící na těleso ve vzdálenosti \(r\) od planety je dána vztahem \(F=\frac{k}{r^2}\), kde \(k\) je konstanta úměrnosti (závislá na hmotnosti planety i tělesa). Toto můžeme slovně vyjádřit tak, že síla je nepřímo úměrná druhé mocnině vzdálenosti. Pro \(r\) rovno jedné je síla \(F\) přímo rovna konstantě \(k\). Konstanta úměrnosti \(k\) proto udává sílu působící na těleso v jednotkové vzdálenosti od planety.
Monotonie funkce
V následující definici jsou nejdůležitější pojmy rostoucí a klesající funkce. Názorně řečeno, jsou to funkce které zachovávají (rostoucí) nebo obracejí (klesající) směr nerovnosti při aplikaci funkce na obě strany nerovnice.
Definice (monotonie funkce).
Nechť \(f\) je funkce a \(M\subseteq \mathrm{Dom}(f)\) podmnožina definičního oboru funkce \(f\).
- Řekneme, že funkce \(f\) je na množině \(M\) rostoucí jestliže pro každé \(x_1, x_2\in M\) s vlastností \(x_1<x_2\), platí \(f(x_1)<f(x_2)\).
- Řekneme, že funkce \(f\) je na množině \(M\) klesající jestliže pro každé \(x_1, x_2\in M\) s vlastností \(x_1<x_2\), platí \(f(x_1)>f(x_2)\).
- Řekneme, že funkce \(f\) je na množině \(M\) (ryze) monotonní je-li buď rostoucí, nebo klesající na \(M\).
Nespecifikujeme-li množinu \(M\), máme na mysli, že uvedená vlastnost platí na celém definičním oboru funkce \(f\).
Poznámka (monotonie z hlediska řešitelnosti nerovnic).
Je-li funkce \(f\) rostoucí nebo klesající, je i prostá a nerovnice uvedené v předchozí definici jsou dokonce ekvivalentní. Můžeme tedy na obě strany nerovnice aplikovat tutéž rostoucí funkci, nebo rostoucí funkci z obou stran nerovnice vynechat.
- Je-li \(f\) rostoucí, platí \[x_1\leq x_2 \iff f(x_1)\leq f(x_2).\]
- Je-li \(f\) klesající, platí \[x_1\leq x_2 \iff f(x_1)\geq f(x_2).\]
- Stejné vztahy platí i pro ostré nerovnosti.
Tyto poučky použijeme vždy, když rozvažujeme, zda můžeme k oběma stranám nerovnice přičíst stejné číslo (můžeme), zda můžeme obě strany nerovnice vynásobit stejným nenulovým číslem (můžeme, ale pokud násobíme záporným číslem, obrací se směr nerovnosti), zda můžeme obě strany nerovnice logaritmovat logaritmem o stejném základě (můžeme, ale v případě logaritmu a základě menším než \(1\) se obrací směr nerovnosti), umocnit (nemůžeme, leda bychom měli dodatečnou informaci například o tom, že obě strany nerovnice jsou kladné nebo obě strany nerovnice jsou záporné) apod. Takových situací je mnoho a protože není v lidských silách si všechny pamatovat, stačí je míst spojeny s definicí rostoucí a klesající funkce.
Příklad (užitečnost monotonie při práci s nerovnicemi). Funkce \(\ln x\) a \(\sqrt x\) jsou rostoucí a proto z nerovnic \[\ln x>\ln 6\] a \[\sqrt x>\sqrt 6\] plyne \[x>6.\] Zejména v druhém případě je nutné si uvědomit, že používáme definici rostoucí funkce a skutečnost, že nezápornost obou stran nerovnice zajišťuje, že pracujeme na intervalu kladných hodnot \(x\), kde je druhé mocnina rostoucí funkce. Nestačí říct, že umocňujeme obě strany nerovnice, jak by někdo mohl tento krok dezinterpretovat. Umocněním obou stran nerovnice se obecně může změnit obor pravdivosti, proto tato operace u nerovnic není povolena. Na celém svém definičním oboru totiž druhá mocnina rostoucí není.
Příklad (nerovnice obsahující nemonotonní funkce). Funkce \(\frac 1x\) a \(y=x^2\) nejsou ani rostoucí ani klesající a proto z žádné z nerovností \[\frac 1x \leq \frac 15\] a \[x^2 \leq 5^2\] neplyne ani \(x\leq 5\) ani \(x\geq 5\). Tento příklad ukazuje, že nerovnice obsahující nemonotonní funkce jsou v obecném případě složitější, protože nemůžeme speciálních vlastností monotonních funkcí. Někdy však není nutné pracovat na celém definičním oboru, ale je možno definiční obor zúžit na množinu, kde funkce již monotonní je. Například funkce \(\sqrt x\) nabývá nezáporných hodnot a funkce \(\frac 1x\) je klesající na \((0,\infty)\). Proto z nerovnosti \[\frac 1{\sqrt x} \leq \frac 15\] plyne \[\sqrt x\geq 5=\sqrt {25}.\] Druhá mocnina je na intervalu \((5,\infty)\) rostoucí a proto odsud plyne dále \[x\geq 25.\]
Přípravné úvahy pro zavedení derivace
Různé pojetí rychlosti

Budeme se zajímat o to, jak rychle se mění funkční hodnoty v čase nebo při změnách vstupních dat. V souvislosti s obrázkem nás může napadnout mnoho významů pojmu rychlost.
- Jakou rychlost (v kilometrech za hodinu) může automobil vyvinout?
- Jak rychle (v kilometrech za hodinu za sekundu) automobil zrychluje?
- Jak rychle (v metrech na kilometr za hodinu) se prodlužuje brzdná dráha při zvyšující se rychlosti?
- Jak rychle (v tisících kilometrů na kilopascal) klesá životnost pneumatik při přehuštění?
- Jak rychle (v litrech na 100 kilometrů na kilometr za hodinu) roste spotřeba auta při vyšší průměrné cestovní rychlosti?
- Jak rychle (v tisících Kč na automobil) rostou náklady výrobce automobilů při zvyšování produkce?
Průměrná rychlost a okamžitá rychlost

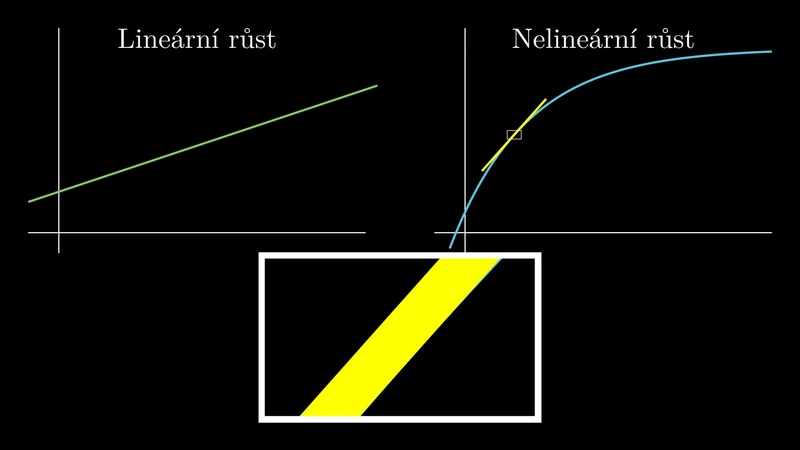
Průměrnou rychlost určujeme tak, že změnu sledované veličiny přepočteme na jednotku času (u závislosti na čase), délky (u závislosti na poloze) nebo obecně na jednotku veličiny, na které sledovaná veličina závisí.
Průměrná rychlost s jakou se mění funkce \(f\) na intervalu \([x,x+h]\) je dána vztahem \[\frac{f(x+h)-f(x)}h.\]
Průměrná rychlost pracuje jenom s informací v koncových bodech intervalu a proto bohužel neobsahuje informaci, co přesně se děje uvnitř intervalu, přes který průměrujeme. Počítáme-li ale průměr přes stále kratší interval, nevýhoda průměrné rychlosti mizí. Cílem je počítat průměr přes interval prakticky nerozlišitelný od nuly. To by dalo okamžitou rychlost. Numerický experiment ukazuje, že u některých funkcí toto funguje pěkně, u některých bohužel ne.
Pokud průměrujeme za stále kratší čas, čitatel i jmenovatel se blíží k nule a jsou potíže s interpretací zlomku. Nulou totiž není možné dělit. Musíme vytvořit koncept, který umožní sledovat, co se děje s funkčními hodnotami funkce, pokud se vstupními daty jdeme “na krev” ke kraji definičního oboru. K tomu použijeme pojem limita. Budeme se (zatím) soustředit na tzv. vlastní limitu ve vlastním bodě. Tím se oproti obecnému postupu mnohé usnadní. Zejména pojem limity můžeme opřít o pojem spojitost, který je přece jenom intuitivnější.
Spojitost

Definice spojitosti zavádí jakousi třídu funkcí, které jsou v jistém smyslu pěkné a můžeme pro ně použít postupy, které pro obecné funkce nefungují. Jsou zde funkce, jejichž funkční hodnoty se mění plynule a nemůžou se změnit skokově. Malá změna ve vstupních datech vyvolá malou změnu ve funkčních hodnotách.
Buď \(f\colon \mathbb R\to\mathbb R\) funkce jedné proměnné.
Definice (okolí).
Okolím bodu \(x_0\) rozumíme libovolný otevřený interval obsahující bod \(x_0\).
Definice (spojitost).
Řekneme, že funkce \(f\) je spojitá v bodě \(x_0\) jestliže je v tomto bodě definovaná a pro libovolnou předem zadanou toleranci (i extrémně malou) existuje okolí bodu \(x_0\) takové, že všechny body z okolí bodu \(x_0\) mají funkční hodnotu v rámci uvažované tolerance nerozlišitelnou od \(f(x_0)\). Řekneme, že funkce \(f\) je spojitá na otevřeném intervalu, je-li spojitá v každém jeho bodě.
Definice spojitosti sice není zcela názorná, ale následující definice a věta velmi pomůže. Zhruba řečeno vysvětlují, proč si v naprosté většině prakticky využitelných případů můžeme spojitost ověřit jenom tím, že zjistíme, zda je funkce definována.
Definice (elementární funkce).
Všechny mnohočleny, goniometrické, cyklometrické, exponenciální a logaritmické funkce a obecná mocnina se nazývají základní elementární funkce Všechny funkce, které ze základních elementárních funkcí získáme konečným počtem operací sčítání, odečítání, násobení, dělení a skládání těchto funkcí navzájem se nazývají elementární funkce.
Věta (spojitost elementárních funkcí).
Všechny elementární funkce jsou spojité v každém vnitřním bodě svého definičního oboru.
Podobně jako spojitost funkce jedné proměnné je definována spojitost funkcí více proměnných. Zůstane dokonce v platnosti předchozí věta. V naprosté většině základních praktických aplikací vystačíme s popisem pomocí elementárních funkcí a proto jsou funkce, se kterými pracujeme, zpravidla automaticky spojité. Opatrnost je nutné pouze tam, kde bychom se od elementárních funkcí odchýlili, například při použití nekonečných řad.
Poznámka.
Body, v jejichž okolí je funkce ohraničená, ale je zde porušena spojitost, jsou například následující.
- skok
- Na jeho odhalení stačí zvolit toleranci v definici spojitosti menší, než je výška skoku. Například \(f(x)=\frac{|x|+x}{2x}\) je jednotkový skok v nule.
- odstranitelná nespojitost
- Tato nespojitost nás zajímá nejvíce. Je to nespojitost, která zmizí pokud vhodně dodefinujeme funkční hodnotu v bodě nespojitosti. Například funkce \[f(x)= \begin{cases} \frac {\sin x}{x}& x\neq 0\\ 1& x=0 \end{cases} \] je spojitá funkce. Vznikla doplněním jedné funkční hodnoty do definice funkce \(\frac{\sin x}x\), která má odstranitelnou nespojitost v bodě \(x=0\).
Limita
Definici limity opřeme o pojem spojitosti. V podstatě pod limitu skryjeme buď funkční hodnotu spojité funkce (pokud existuje), nebo hodnotu, která danou funkci učiní spojitou. Můžeme tedy limitu považovat za “nejlepší rozumnou náhradu” funkční hodnoty v tom smyslu, že po předefinování jedné funkční hodnoty se funkce stane spojitou, tj. relativně pěknou.
Definice (limita).
Nechť \(f\) je funkce definovaná v okolí bodu \(x_0\), s případnou výjimkou bodu \(x_0\). Řekneme, že funkce \(f\) má v bodě \(x_0\) limitu rovnu číslu \(L\), jestliže funkce \(g(x)\) definovaná vztahem \[g(x)= \begin{cases} L& x=x_0\\ f(x)& \text {jinak,}\end{cases}\] je spojitá v bodě \(x_0\). Píšeme \[\lim_{x\to x_0}f(x)=L.\]
Velmi stručně řečeno: pokud se nedá nějaké číslo do funkce dosadit přímo, mohlo by to jít pomocí limity. Například funkce \[\frac{\sin x}{x}\] není definována v nule. V okolí nuly se však chová v jistém smyslu pěkně: má funkční hodnoty prakticky nerozlišitelné od jedničky, viz graf v odstavci věnovanému spojitosti. Proto platí \[\lim_{x\to 0}\frac{\sin x}{x}=1.\]
Derivace
Teď jsme připraveni (alespoň teoreticky) počítat průměrnou rychlost na intervalu, jehož délka je nerozlišitelná od nuly. Vypočteme průměrnou rychlost na intervalu délky \(h\) a poté položíme \(h\) rovno nule. Ve smyslu limity, pokud je to nutné.
Buď \(y=f(x)\) funkce definovaná na nějakém otevřeném intervalu.
Definice (derivace).
Derivací funkce \(f\) v bodě \(x\) rozumíme limitu \[\frac{\mathrm df}{\mathrm dx}:=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}.\]
Derivaci funkce \(f\) v bodě \(x_0\) označujeme \(f'(x_0)\) nebo \(\frac{\mathrm df(x_0)}{\mathrm dx}\). Derivaci v libovolném bodě potom \(f'\), \(f'(x)\) nebo \(\frac{\mathrm df}{\mathrm dx}\). Zápis \(\frac{\mathrm df}{\mathrm dx}\) je Leibnizova notace, zápis \(f'\) je Lagrangeova notace.
Poznámka (slovní interpretace definice derivace).
- Výraz z čitatele, tj. \(f(x+h)-f(x)\), je změna veličiny \(f\) na intervalu \([x,x+h]\). Často označujeme též \(\Delta f\).
- Podíl, tj. \(\frac{f(x+h)-f(x)}h\) je změna veličiny \(f\) na intervalu \([x,x+h]\) přepočítaná na jednotku veličiny \(x\), tj. v jistém smyslu průměrná rychlost na tomto intervalu. Často označujeme též \(\frac{\Delta f}{\Delta x}\).
- Limita v definici derivace stahuje délku intervalu, na kterém počítáme průměrnou rychlost, k nule. Tím se z průměrné rychlosti stane okamžitá rychlost.
| Část definičního vztahu | Slovní interpretace |
|---|---|
| \(f(x)\) | funkční hodnota v bodě |
| \(f(x+h)\) | funkční hodnota ve vedlejším bodě |
| \(f(x+h)-f(x)\) | změna funkce na intervalu \([x,x+h]\) |
| \(\displaystyle\frac{f(x+h)-f(x)}{h}\) | průměrná rychlost změny funkce na intervalu \([x,x+h]\), též změna funkce po přepočtu na interval jednotkové délky |
| \(\displaystyle\lim_{h\to 0}\cdots\) | limita pro redukci průměrné rychlosti na okamžitou |
| \(\displaystyle\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\) | okamžitá rychlost změny funkce v bodě \(x\), derivace |
Interpretace derivace v nematematických disciplínách je okamžitá rychlost s jakou veličina \(f\) reaguje na změny veličiny \(x\). Často studujeme veličiny závislé na čase s v tomto případě jde tedy o rychlost, s jakou se veličina mění v čase. Další možnosti a obraty používané pro slovní vyjádření derivace jsou zmíněny níže v podkapitole věnované derivaci podle času. Analogickou terminologii (rychlost růstu, rychlost změny) zpravidla přenášíme i na případy, kdy nezávislou proměnnou není čas. Rychlost potom chápeme v abstraktním slova smyslu.
Obecně, ať již je nezávislou proměnnou čas či jiná veličina, se derivace \(f'(x)\) často slovně interpretuje jako změna veličiny \(f\), odpovídající změně veličiny \(x\) o jednotku. Je to podobné, jako údaj o rychlosti na tachometru v automobilu. Ten udává, kolik kilometrů ujedeme za hodinu. Od skutečně uražené dráhy se tento údaj může lišit, protože pohyb může trvat třeba jenom deset minut. A kdyby jízda opravdu trvala hodinu, mohlo vlivem jízdy v zácpě dojít k podstatnému nesouladu se skutečně uraženou dráhou. Přesto je okamžitá rychlost ukazovaná na tachometru při jízdě automobilem užitečná veličina a nemáme problémy s jejím chápáním. Stejně tak pohlížejme na derivaci.
Testová otázkaPoznámka (jednotka derivace).
Jednotka derivace \(\frac{\mathrm df}{\mathrm dx}\) funkce \(f(x)\) je stejná, jako jednotka podílu \(\frac {f(x)}x\).
Věta (existence derivace implikuje spojitost).
Má-li funkce \(f\) derivaci na intervalu \(I\), je na tomto intervalu spojitá.
Věta (znaménko derivace implikuje monotonii).
- Má-li funkce \(f\) kladnou derivaci na intervalu \(I\), je na tomto intervalu rostoucí.
- Má-li funkce \(f\) zápornou derivaci na intervalu \(I\), je na tomto intervalu klesající.
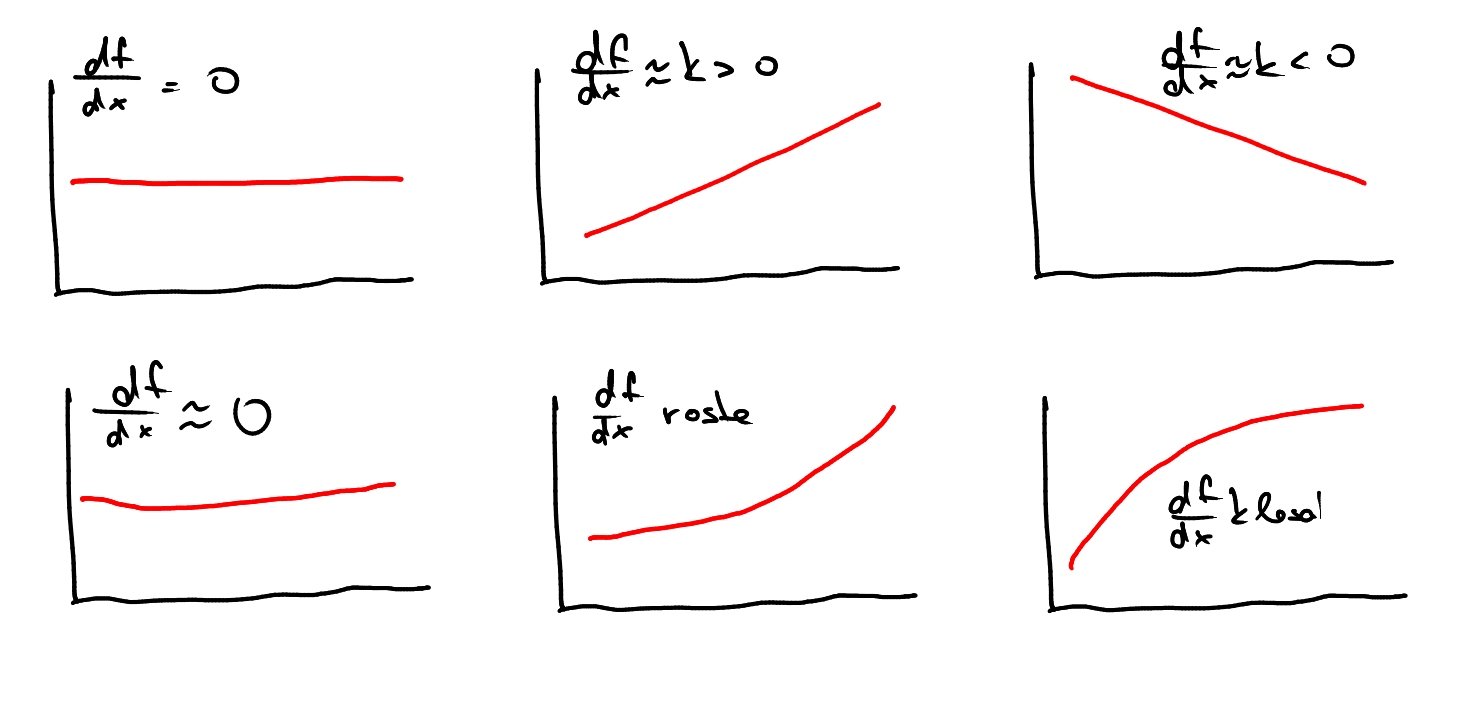
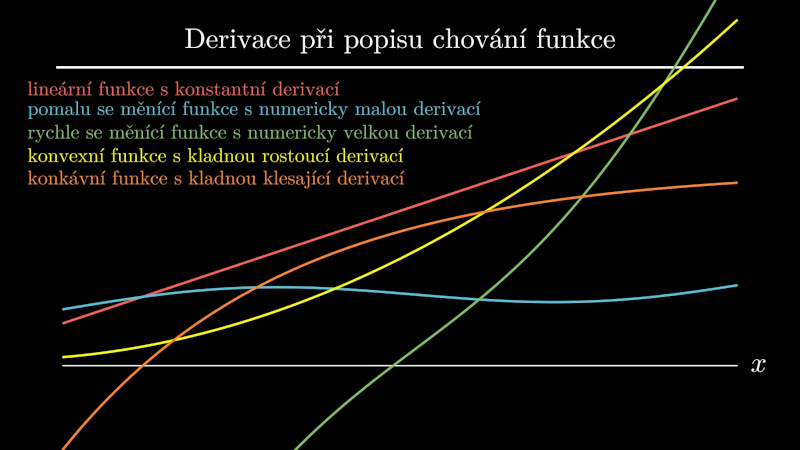
| Derivace funkce | Chování funkce |
|---|---|
| Derivace je nulová. | Funkce je konstantní. Sledovaná veličina se nemění při změně vstupních dat. |
| Derivace je kladná. | Funkce roste. Pokud data na vstupu rostou, sledovaná veličina také roste. |
| Derivace je záporná. | Funkce klesá. Pokud data na vstupu rostou, sledovaná veličina klesá. |
| Derivace je numericky malá (blízká k nule). | Funkce se mění pomalu. Sledovaná veličina reaguje na změny ve vstupních datech pouze málo. |
| Derivace je numericky velká (hodně kladná nebo hodně záporná). | Funkce se mění rychle. Malá změna na vstupu má velký vliv na sledovanou veličinu. |
| Derivace je konstantní. | Funkce je lineární. Klesá nebo roste pořád stejně rychle. Pokud vstup roste aritmetickou řadou (po stejných skocích), sledovaná veličina roste nebo klesá také aritmetickou řadou. |
| Derivace roste. | Funkce je nelineární a roste stále rychleji. Pokud je funkce kladná, rostoucí derivace znamená, že růst se stále zrychluje. |
| Derivace klesá k nule. | Funkce je nelineární a přibližuje se k vodorovné asymptotě. Pokud je funkce kladná, k nule klesající derivace znamená, že růst se stále zpomaluje a zastaví se. |
Aplikace derivací 1: Jak rychle? (změna v čase)
Poznámka (slovní vyjádření derivace podle času).
Derivace v bodě, pokud ji nahlížíme z hlediska časové změny veličiny, je okamžitá rychlost s jakou se mění tato veličina. Protože kladná změna je růst, nahrazujeme někdy slovo “změna” slovem “růst”. Protože rychlost je změna za jednotku času, nahrazujeme někdy slovo “rychlost” obratem “změna za jednotku času”. Derivaci podle času můžete tedy přečíst libovolným z následujících obratů. Všechny se běžně používají a všechny chápeme stejně – jako derivaci podle času.
- Rychlost růstu
- Rychlost změny (implicitně předpokládáme, že kladná změna odpovídá růstu a záporná změna poklesu)
- Nárůst za jednotku času
- Změna za jednotku času
- Časová změna veličiny
Pokud potřebujeme pracovat s poklesem, násobíme derivaci faktorem \(-1\). Toto čteme též jako “záporně vzatá derivace.”

Zákon ochlazování
Horké těleso o teplotě \(T\) je v chladnější místnosti o teplotě \(T_0\). Z fyziky je známo (Newtonův zákon tepelné výměny), že rychlost s jakou klesá teplota tělesa je úměrná teplotnímu rozdílu. Tento rozdíl je \(T-T_0\) (od většího odečítáme menší).
- Veličina \(T\) je teplota tělesa měřená například ve stupních Celsia.
- Veličina \(t\) je čas měřený například v hodinách.
- Derivace \(\frac{\mathrm dT}{\mathrm dt}\) ve stupních Celsia za hodinu je rychlost, s jakou roste teplota tělesa.
- Pokud je například derivace kladná a rovna hodnotě \(5\) stupňů Celsia za hodinu, znamená to, že teplota roste rychlostí \(5\) stupňů Celsia za hodinu.
- Pokud je například derivace záporná a rovna hodnotě \(-5\) stupňů Celsia za hodinu, znamená to, že teplota klesá rychlostí \(5\) stupňů Celsia za hodinu.
- Pokud je derivace dána vztahem \(-e^{-t}\), kde \(t\) je čas v hodinách a derivace vychází ve stupních Celsia za hodinu, využijeme toho, že \(e^0=1\) a \(e^{-1}=0.37\). To znamená, že na počátku se teplota snižuje okamžitou rychlostí jeden stupeň Celsia za hodinu, tato rychlost ochlazování se pozvolna mění a například po hodině se teplota snižuje už jenom rychlostí \(0.37\) stupně Celsia za hodinu.
- Matematickým vyjádřením toho, že rychlost s jakou se mění teplota je úměrná teplotnímu rozdílu \(T-T_0\) je rovnice \[\frac{\mathrm dT}{\mathrm dt}=-k(T-T_0),\] kde \(k\) je konstanta úměrnosti a záporné znaménko vyjadřuje, že teplota klesá. Konstanta \(k\) je číselně rovna rychlosti ochlazování v situaci, kdy je jednotkový rozdíl mezi teplotou objektu a okolí.
- Neznámou v sestavené rovnici je funkce a v rovnici figuruje derivace této funkce. Takové rovnice se naučíme řešit později.
V této chvíli je pro nás cenné to, že umíme přeformulovat fyzikální popis vývoje (rychlost změny teploty je úměrná rozdílu teplot) na kvantitativní popis, kde dokážeme realizovat numerickou simulaci. Realizace takové simulace může vypadat například tak, že na krátký časový krok budeme předpokládat konstantní rychlost. Tuto rychlost použijeme pro odhad nové teploty, tato nová teplota změní teplotní rozdíl, tím se změní i rychlost a postup opakujeme. Toto děláme na počítači.
Poznámka (smysl příkladu se zákonem ochlazování).
Předchozí příklad je často v různých obměnách používán na modelování ochlazování kávy, což je proces, který většina lidí důvěrně zná. Nemáme pochopitelně ambice se domnívat, že bychom dokázali z této rovnice odvodit nějaké zásadní výsledky aplikovatelné při pití ranní kávy nebo při konzumaci horké polévky. Učíme se na malých věcech, abychom později mohli dělat věci velké. Na známých věcech se učíme aparát, který bude naším jediným nástrojem tam, kde intuice začne selhávat. Z tohoto příkladu je nutné si odnést, že derivace, jako rychlost změny, hraje roli při kvantitativním popisu dějů a při studia procesů, kdy se mění veličiny. Ať už doopravdy (studium pohybu nebo dějů, probíhajících v čase) nebo virtuálně (problémy spojené s mechanikou, včetně statiky, stability a deformací, často pracují s virtuálními změnami, tj. se změnami, které jsou sice z hlediska úlohy přípustné, ale příroda je z nějakého důvodu nerealizuje). Tedy naprostá většina dějů a jevů, které studujeme a chceme jim rozumět. Jakmile se v popisu fyzikálního zákona objeví slovo rychlost, někdy nahrazené souslovím časová změna, znamená to, že kvantitativní popis se děje pomocí derivací.
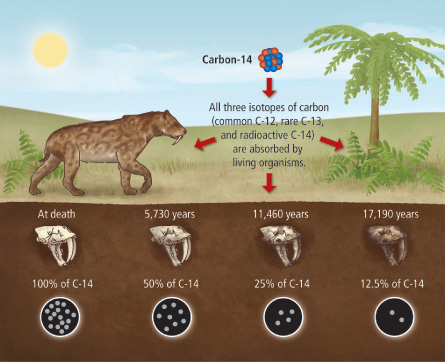
Uhlík 14C a datování organických nálezů
V roce 1940 byl objeven uhlík \(^{14}C\). Jedná se o radioaktivní prvek s mnoha skvělými vlastnostmi. Jednou z nich je vhodná rychlost rozpadu, která jej činí vhodným pro datování archeologických nálezů pozůstatků živých organismů
- Rychlost, s jakou se mění množství (a tedy i koncentrace \(y\) v daném vzorku) nerozpadnutého radioaktivního materiálu je úměrná jeho množství (a tedy i koncentraci). Tato skutečnost je přirozeným důsledkem toho, že pro daný nestabilní izotop mají všechny atomy stejnou pravděpodobnost, že u nich dojde k rozpadu a tato pravděpodobnost se s časem nemění. Kvantitativně je proces rozpadu popsán rovnicí \[\frac{\mathrm dy}{\mathrm dt}=-\lambda y,\] kde \(\lambda\) je konstanta úměrnosti.
- Konstanta úměrnosti \(\lambda\) vyjadřuje rychlost, s jakou se rozpadá jednotkové množství látky.
- Uhlík je na datování vhodný, protože jej během života absorbují živé organismy a protože poločas rozpadu jej činí vhodným pro datování většiny archeologicky zajímavých nálezů. (Pro datování vzorků starších než 50 tisíc let je nutné použít jiný prvek, protože v tomto případě již uhlíku \(^{14}C\) ve vzorku zůstane málo.)
Aplikace derivací 2: Jak strmě? (změna v prostoru)
Derivace v bodě můžeme nahlížet z hlediska prostorové změny veličiny. Tím zjistíme, jak nerovnoměrně je veličina rozložena v prostoru. Často se derivace podle prostorové proměnné nazývá gradient, zejména pokud nepracujeme v jednorozměrném případě, ale pokud popisujeme děj probíhající v rovině nebo v prostoru.
Vedení tepla (dřevařství, nábytek, dřevostavby)
Nerovnoměrnost rozložení teploty v tělese vede k vyrovnávání teplot přenosem tepla. Uvažujme teplotu \(T\) tyče jako funkci polohy \(x\) na tyči. Ke kvantitativnímu vyjádření vedení tepla je nutné vědět, jaký rozdíl teplot připadá na jednotku délky. V homogenním případě vydělíme teplotní rozdíl vzdáleností. V obecném případě rychlost s jakou se mění teplota podél tyče (gradient teploty) vyjadřujeme pomocí derivace \[\frac{\mathrm dT}{\mathrm dx}.\] Využívá se v posuzování izolačních vlastností a při sušení dřeva.
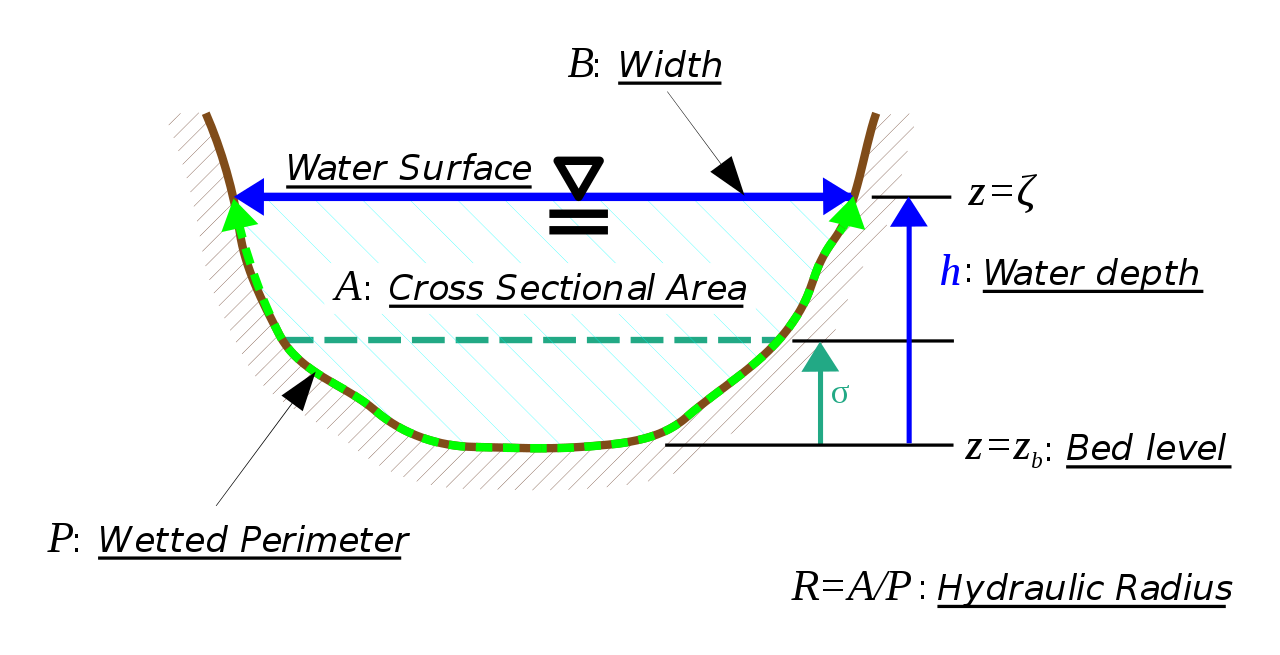

Koryto řeky (krajinářství)
Uvažujme příčný řez korytem řeky, jak je na obrázku. Z tohoto obrázku je zřejmé, že při zvyšování obsahu průřezu roste hladina. Pokud by stěny byly svislé (tj. \(B\) nezávislé na \(h\)), byla by změna průřezu \(\Delta A\) (například v milimetrech čtverečních) vyvolaná změnou výšky \(\Delta h\) (například v milimetrech) rovna šířce řeky \(B\) v milimetrech, protože koryto by bylo obdélníkové a podíl obsahu obdélníka a jeho výšky je šířka. V případě nekonstantního \(B\) dostáváme místo podílu derivaci, tj. \[\frac{\mathrm d A}{\mathrm dh}=B.\] Derivace průřezu koryta podle výšky koryta hraje důležitou roli například při přechodu říčního proudění v bystřinné. Tato veličina vyjadřuje, jak rychle se mění obsah průřezu s rostoucí hladinou. V praxi je možné ji spočítat pro speciální tvary koryta, proto jsou vzorce pro vodní skok související s tímto přechodem k dispozici jenom ve speciálních případech, jako například koryto obdélníkového tvaru.
Výpočet derivace
- Nikdy (nebo alespoň skoro nikdy) nederivujeme pomocí definice, ale používáme vzorce pro derivace základních elementárních funkcí a pro derivace matematických operací s funkcemi.
- Viz cvičení v prvním týdnu.
Derivování si také můžete procvičit v následujících cvičeních. Se zápisem matematických výrazů Vám může pomoci tento cheatsheet.
Testová otázka Testová otázka Testová otázka Testová otázka Testová otázka Testová otázka Testová otázka Testová otázka Testová otázka Testová otázka Testová otázkaVztah mezi rychlostmi měnících se veličin

Pokud existuje mezi dvěma veličinami známý vztah, můžeme pomocí derivací odvodit vztah mezi rychlostmi, s jakými se tyto veličiny mění. Ukážeme si to na příkladu kyvadla. Podobně se chová strom s dlouhým kmenem a korunou nahoře, například listnaté stromy v lese.
Perioda matematického kyvadla délky \(L\) je dána vzorcem \(T=2\pi \sqrt{\frac Lg}\). Tento vzorec je možno přepsat do tvaru \[T=\frac{2\pi}{\sqrt g} \sqrt L, \] který ukazuje, že perioda je úměrná odmocnině délky kyvadla.
Pro derivování použijeme vzorec pro derivaci konstantního násobku a mocninné funkce. \[\frac {\mathrm d T}{\mathrm dL}=\frac{\mathrm d}{\mathrm dL}\left(\frac{2\pi}{\sqrt g} \sqrt L\right)=\frac{2\pi}{\sqrt g} \frac{\mathrm d}{\mathrm dL}\left (L^{\frac 12}\right)=\frac{2\pi}{\sqrt g}\frac 12 L^{-\frac 12}=\frac{\pi}{\sqrt{gL}}. \] Tento výraz udává v jednotkách sekunda na metr, jak rychle se prodlužuje perioda kyvadla při prodloužení délky kyvadla. Například pro \(L=2\,\mathrm m\) je derivace číselně rovna \(0.71\,\mathrm{s}\,\mathrm{m}^{-1}.\) Prodloužení dvoumetrového kyvadla o metr prodlouží periodu o \(0.71\) sekundy. Protože derivace je okamžitá rychlost změny a na delším intervalu se tato rychlost může změnit, je blíže realitě spíše formulace pro jednotky tisíckrát menší: “Prodloužení kyvadla o milimetr prodlouží periodu o \(0.71\) milisekundy.”
Pokud se kyvadlo délky \(L=2\,\mathrm m\) prodlužuje (po přenesení ze zimy do vytopené místnosti se závěs se prodlužuje teplotní roztažností), je rychlost prodlužování \(\frac{\mathrm dL}{\mathrm dt}\) a rychlost, s jakou roste perioda je (s použitím pravidla pro derivaci složené funkce) \[ \frac{\mathrm dT}{\mathrm dt} = \frac{\mathrm dT}{\mathrm dL} \frac{\mathrm dL}{\mathrm dt} = \frac{\pi}{\sqrt {gL}}\frac{\mathrm dL}{\mathrm dt}\] Pokud se kyvadlo prodlužuje rychlostí \(0.5\) milimetru za sekundu, je \[\frac{\mathrm dL}{\mathrm dt}=0.000\,5\,\mathrm{m}\,\mathrm{s}^{-1}\] a \[\frac{\mathrm dT}{\mathrm dt} =\frac {\pi}{\sqrt{2\cdot 9.81}} 0.000\,5=0.00035\] Derivace vychází bez jednotky (sekunda lomeno sekundou se zkrátí) a je možné ji přepsat do tvaru \[\frac{\mathrm dT}{\mathrm dt} =0.35 \frac{\mathrm{ms}}{\mathrm{s}}.\] Perioda kyvadla se prodlužuje rychlostí \(0.35\) milisekundy za sekundu.
Rychlost nabíjení kondenzátoru

Elektrický odpor dřeva a mnoha dalších stavebních materiálů souvisí s vlhkostí a tato souvislost je umožňuje sestrojení vlhkoměru. Protože elektrický odpor těchto materiálů je velký, není vhodné pro určení elektrického odporu použít Ohmův zákon a změřený proud a napětí. Jedna z možností je měření času nutného k nabití nebo vybití kondenzátoru přes odpor. Napětí \(U\) na kondenzátoru o kapacitě \(C\) souvisí s nábojem na kondenzátoru vztahem \[U=\frac 1C Q.\] Derivováním tohoto vztahu podle času dostaneme vztah mezi rychlostmi změn těchto veličin ve tvaru \[\frac{\mathrm dU}{\mathrm dt}=\frac 1C \frac{\mathrm dQ}{\mathrm dt}.\] Veličina \(\frac{\mathrm dQ}{\mathrm dt}\) je nabíjecí proud. Ten dokážeme určit analýzou elektrického obvodu, jak si ukážeme v přednášce o diferenciálních rovnicích. Tím budeme znát derivaci \(\frac{\mathrm dU}{\mathrm dt}\) a najít napětí jako funkci času z derivace se naučíme v přednášce o integrálech. Důležitým prvním krokem při analýze uvažovaného elektrického zapojení je však souvislost časové změny napětí a časové změny náboje, tj. derivace dvou souvisejících veličin.
Funkce více proměnných
Funkce má na vstupu více proměnných, na výstupu reálné číslo. Některé pojmy, jako například monotonie, ztrácejí ve světě funkcí více proměnných smysl, například monotonie nebo inverzní funkce. Proměnné značíme pomocí jejich fyzikálního označení. Bez fyzikálního kontextu zpravidla používáme funkce dvou, tří, nebo \(n\) proměnných v následujícím tvaru.
- \(f:\mathbb R^2\to\mathbb R\), \(f(x,y)\) Geometricky můžeme chápat jako výšku přiřazenou bodu v rovině a výsledkem je plocha ve 3D, nebo barvu přiřazenou bodu v rovině a výsledkem je obarvená rovina.
- \(f:\mathbb R^3\to\mathbb R\), \(f(x,y,z)\) Geometricky můžeme chápat jako barvu přiřazenou bodu v prostoru a výsledkem je obarvený prostor.
- \(f:\mathbb R^n\to\mathbb R\), \(f(x_1,x_2,\dots,x_n)\) Geometrická představa zde není možná, chápeme čistě abstraktně.
Myšlenka na zavedení derivace funkce více proměnných

Derivace je vhodná ke studiu fyzikálních procesů na makroskopické úrovni těles. Pro vyjadřování procesů jako jsou rychlost změny teploty tělesa nebo množství tekutiny v daném objemu jsou vhodné (obyčejné) derivace.
Například při studiu tepelného pole v materiálech rozlišujeme (pomocí takzvaného Biotova čísla) na jednu stranu případy, kdy vedení tepla není podstatné a těleso lze uvažovat jako celek mající ve všech částech stejnou teplotu, a na druhou stranu případy, kdy je nutné pracovat s prostorovým rozložením tepla v tělese. Druhá varianta typicky nastává například u úloh na tepelnou modifikaci dřeva, kdy teplo prostupuje do vzorku a musíme být schopni modelovat tento proces. Teplota se mění s časem i s polohou. Skutečně, v jeden okamžik mohou mít různé body různou teplotu a proto teplota závisí na poloze. Podobně, v daném místě se teplota může zvyšovat i snižovat a proto teplota závisí i na čase. Při modelování takového procesu již musíme znát teplotu nejen jako funkci času, ale i jako funkci prostorových souřadnic. Musíme tedy být schopni pracovat modelem, kdy teplota, nebo obecně nějaká stavová veličina, závisí na více faktorech. To si vynucuje práci s funkcemi více proměnných a studium toho, jak se mění vzhledem k jednotlivým proměnným. To je přesně úkol pro diferenciální počet funkcí více proměnných a parciální derivace.
Výsledkem tohoto přístupu je formulace zákonů v diferenciálním tvaru. Tento tvar říká, co se děje v konkrétním místě a dává lepší náhled na fyzikální podstatu. Tento přístup používáme, pokud není možný makroskopický pohled na těleso jako na jeden celek.
Parciální derivace
Změna funkce více proměnných může být způsobena změnou libovolné nezávislé proměnné. Pokud sledujeme například ve stěně měnící se teplotní profil, zajímá nás, jak se teplota v jednotlivých místech stěny mění v čase a jak se teplota mění v řezu stěnou. Zdá se býti rozumné oddělit obě změny a studovat každou samostatně. Buď v daném bodě fixovat polohu a sledovat časový vývoj v tomto bodě, nebo v daném čase udělat něco jako teplotní snímek a srovnávat teplotu ve vybraném bodě s okolními teplotami ve stejném čase. To vede k následujícímu přístupu, kdy u funkce více proměnných sledujeme reakci na změnu jedné jediné veličiny.
Následující definice výše uvedenou myšlenku odděleného sledování změny funkce (závislé veličiny) jako reakce na změnu jedné jediné vstupní informace (jedné nezávislé veličiny) uvádí v život. Definice je stejná jako u derivace funkce jedné proměnné, změna je pouze v tom, že je přítomna i další proměnná.
Definice (parciální derivace).
Buď \(f\colon \mathbb R^2\to\mathbb R\) funkce dvou proměnných, \(x\) a \(y\), tj. \(f(x,y)\). Výraz \[\frac{\partial f}{\partial x}:=\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}h\] se nazývá parciální derivace funkce \(f\) podle \(x\). Podobně, \[\frac{\partial f}{\partial y}:=\lim_{h\to 0}\frac{f(x,y+h)-f(x,y)}h\] je parciální derivace funkce \(f\) podle \(y\).
Podobně můžeme definovat parciální derivaci pro funkce libovolného konečného počtu proměnných. V těchto parciálních derivacích vlastně sledujeme, jak reaguje veličina \(f\) na změny jenom v jedné proměnné. Proměnná, přes kterou se nederivuje, má vlastně roli parametru, nijak se nemění.
Rovnice vedení tepla v 1D
Studujme vedení tepla v jednorozměrné tyči. Teplota je funkcí dvou proměnných, polohy a času. Tedy \(T=T(t,x).\) Parciální derivace \(\frac{\partial T}{\partial t}\) udává je rychle (například ve stupních Celsia za hodinu) roste v daném místě teplota. V různých částech desky může být tato veličina jiná a vždy se vztahuje k danému bodu. Přirozeně se mění i v čase, například v prostředí s konstantní teplotou postupně systém dospěje do stavu se stacionárním rozložením teploty, kdy se teplota v žádném místě ani neroste ani neklesá a parciální derivace podle času je nulová. Derivace \(\frac{\partial T}{\partial x}\) udává jak prudce (například ve stupních Celsia na centimetr) roste teplota ve směru osy \(x\).
Poznámka.
Potřebujeme fyzikální zákony řídící vedení tepla. Bez nich matematika model vedení tepla nemá jak naformulovat. Tyto zákony je potřeba matematice dodat “z venku”, z aplikované vědy. Tou je v tomto případě fyzika, jindy může být biologie nebo geologie. Jakmile jsou potřebné zákony a případně materiálové vztahy k dispozici, stává se problém čistě matematickým a fyzika přijde ke slovu při závěrečné interpretaci. Použijeme následující fyzikální fakta.
- Rozdílem teplot je způsoben tok tepla. Velikost toku tepla je úměrná teplotnímu rozdílu a teplo teče z místa v větší teplotou do místa s menší teplotou.
- Teplota se zvyšuje dodáním tepla. Změna teploty je úměrná dodanému teplu.
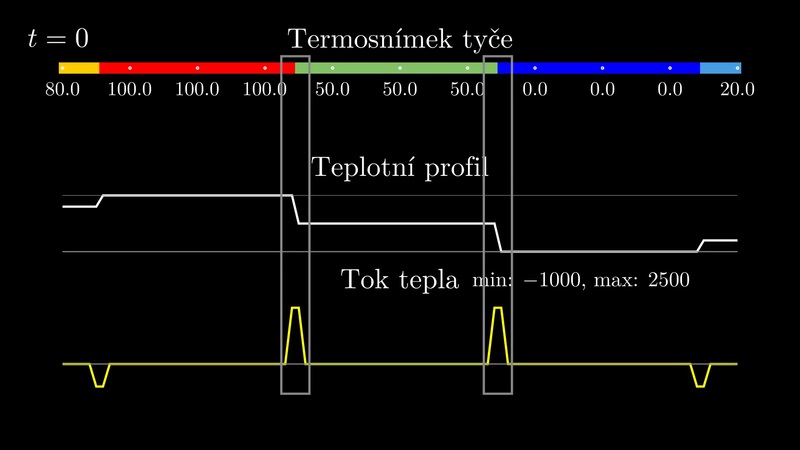
V dalším už nastupuje matematický popis a ve vhodných chvílích vždy použijeme výše uvedené fyzikální zákony. Mluvíme o teple, ale jako mechanický model si můžeme představit proudění tekutiny (pro jednoduchou představu) nebo proudění vlhkosti (pro odvození rovnice difuze namísto rovnice vedení tepla). Budeme uvažovat libovolné místo materiálu a budeme matematicky vyjadřovat děje, které přispívají ke změně teploty.
- Rychlost s jakou s daném místě roste teplota (v čase) je \[\frac{\partial T}{\partial t}\] a měříme ji například ve stupních Celsia za minutu. Tato rychlost je úměrná rychlosti s jakou do daného místa dodáváme teplo. Proto v dalším budeme hledat rychlost dodávání tepla a daného místa a poté se sem vrátíme a dáme tuto rychlost do souvislosti s rychlostí růstu teploty.
- Je-li například parciální derivace \(\frac{\partial T}{\partial t}\) rovna \(2^{\circ}\mathrm{C}/\mathrm{min}\), znamená to, že v daném místě roste teplota v čase rychlostí dva stupně Celsia za minutu.
- Pokud je parciální derivace záporná a rovna například hodnotě \(-2^{\circ}\mathrm{C}/\mathrm{min}\), znamená to, že teplota v tomto místě klesá rychlostí dva stupně Celsia za minutu.
- Rychlost s jakou s daném místě roste teplota jako funkce polohy je \(\frac{\partial T}{\partial x}\) a měříme ji například ve stupních Celsia na centimetr.
- Je-li například parciální derivace \(\frac{\partial T}{\partial x}\) rovna \(2^{\circ}\mathrm{C}/\mathrm{cm}\), znamená to, že v daném místě roste teplota ve směru osy \(x\) tak, že na každém centimetru naroste o dva stupně Celsia.
- Pokud je parciální derivace záporná a rovna například hodnotě \(-2^{\circ}\mathrm{C}/\mathrm{cm}\), znamená to, že ve směru osy \(x\) teplota klesá a na každém centimetru klesne o dva stupně Celsia.
- Pro přepočet nerovnoměrného rozložení teploty na tok tepla nás zajímá nikoliv jak teplota v prostoru roste, ale jak klesá. Proto musíme vzít derivaci podle prostorové proměnné záporně, abychom dostali pokles teploty.Tento pokles vynásobíme konstantou, která převede spád teploty na tok tepla. Tuto konstantu označíme \(k\) (nazývá se součinitel tepelné vodivosti a dodá nám ji fyzika, přesněji Fourierův zákon) a tok tepla \(q\) ve směru osy \(x\) je \[q=-k\frac{\partial T}{\partial x}.\] To je veličina, která udává, kolik joulů tepla proteče průřezem za jednotku času.
- Je-li \(q\) rovno \(7\,\mathrm{J}/\mathrm{min}\) znamená to, že průřezem proteče ve směru osy \(x\) sedm joulů za minutu.
- Je-li \(q\) záporné a rovno \(-7\,\mathrm{J}/\mathrm{min}\), znamená to, že sedm joulů za minutu proteče v daném místě proti směru osy \(x\).
- Pokud do daného místa přitéká teplo stejnou rychlostí jako odtéká, teplota se nemění a dané místo se ani neohřívá ani neochlazuje. Intenzita ochlazování je dána bilancí mezi přítokem a odtokem. Můžeme si to představit tak, že z tepla které do daného bodu přiteče, se část “oddělí” a přispěje k navýšení teploty a zbytek teče dál. Pro zjištění, kolik tepla se z toku “oddělí” a způsobí v daném místě navýšení teploty potřebujeme vědět, jak rychle v daném místě tok klesá jako funkce proměnné \(x\). Nárůst určíme derivací podle \(x\) a pokles z nárůstu uděláme změnou znaménka. Pokles toku tepla je tedy \[-\frac{\partial q}{\partial x}=
-\frac{\partial }{\partial x}\left(-k\frac{\partial T}{\partial x}\right)=
\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right).
\]
- Například pokles \(-\frac{\partial q}{\partial x}=2\,\mathrm{J}/(\mathrm{min}\,\mathrm{cm})\) toku \(q=10\,\mathrm{J}/\mathrm{min}\) znamená, že o centimetr dál ve směru osy \(x\) proteče průřezem směrem doprava už nikoliv deset, ale pouze osm joulů za minutu.
- Stejný pokles u toku \(q=-10\,\mathrm{J}/\mathrm{min}\) znamená, že v daném místě proteče směrem doleva deset joulů za minutu, ale o centimetr více vpravo je o \(2\) méně, tj. \(-10-2=-12\) a směrem doleva teče dvanáct joulů za minutu.
- V obou případech intenzita toku klesá podél tohoto toku. Tok slábne.
- Pokles toku vypočtený v předchozím bodě je úměrný rychlosti růstu teploty. Příslušné konstanty úměrnosti dodá fyzika a platí \[\frac{\partial}{\partial x}\left(k\frac{\partial T}{\partial x}\right)=\rho c\frac{\partial T}{\partial t},\] kde \(c\) je měrná tepelná kapacita a \(\rho\) je hustota. (V tomto případě jsou hustota i měrná tepelná kapacita vztaženy ne k jednotce objemu, jak jsme zvyklí, ale k jednotce délky. Například \(\rho\) je lineární hustota, tj. v gramech na centimetr).
- Například pokles \(-\frac{\partial q}{\partial x}=2\,\mathrm{J}/(\mathrm{min}\,\mathrm{cm})\) toku \(q=10\,\mathrm{J}/\mathrm{min}\) znamená, že o centimetr dál ve směru osy \(x\) proteče průřezem směrem doprava už nikoliv deset, ale pouze osm joulů za minutu. Tedy každou minutu se v jenom centimetru délky od toku “odpojí” energie o velikosti dva jouly a ta se “uloží” do materiálu. Navenek se to projeví ohřevem, přičemž hrají roli fyzikální vlastnosti materiálu.
- Rovnice odvozená v předchozím kroku se nazývá rovnice vedení tepla a dokáže modelovat například prostup tepla stěnou domu. Tato rovnice zachycuje matematicky to, jak funguje vedení tepla.
Shrnutí. V odvození vidíme, že rovnice vedení tepla je vlastně bilance toku tepla. Hodnota o kolik se v daném místě snižuje tok tepla udává, kolik tepla se v daném místě spotřebovalo. Tato spotřeba tepla se projeví zvýšením teploty v daném bodě.
| Část rovnice vedení tepla | Slovní interpretace |
|---|---|
| \(\color{red}\displaystyle\frac{\partial T}{\partial t}\) | Rychlost s jakou roste v daném místě teplota jako funkce času. |
| \(\displaystyle\frac{\partial T}{\partial x}\) | Rychlost s jakou roste v daném okamžiku teplota podél tyče. |
| \(\displaystyle-\frac{\partial T}{\partial x}\) | Rychlost s jakou klesá v daném okamžiku teplota podél tyče. Záporně vzatá rychlost růstu. |
| \(\displaystyle-k\frac{\partial T}{\partial x}\) | Tok tepla. Podle Fourierova zákona je úměrný rychlosti s jakou klesá teplota. |
| \(\displaystyle\frac{\partial}{\partial x}\left(-k\frac{\partial T}{\partial x}\right)\) | Rychlost s jakou roste tok tepla podél tyče. |
| \(\displaystyle-\frac{\partial}{\partial x}\left(-k\frac{\partial T}{\partial x}\right)\) | Rychlost s jakou klesá tok tepla podél tyče. Toto teplo zůstává v daném místě tyče a projeví se nárůstem teploty v tomto místě. |
| \(\color{red}\displaystyle\frac{\partial}{\partial x}\left(k\frac{\partial T}{\partial x}\right)\) | Upravený výraz z předchozího řádku. Rychlost s jakou klesá tok tepla podél tyče. |
| Rovnice vedení tepla | Červené výrazy jsou si úměrné. |
Poznámka. Vyřešit rovnici vedení tepla je bohužel možné jenom v poměrně speciálních případech, které jsou z praktického hlediska málo významné. Existuje však řada numerických metod jak tuto rovnici vyřešit přibližnými metodami. Tato rovnice je potom “schována” například v softwarech umožňujících vizualizovat tepelné namáhání v okolí kritických prvků staveb, jako jsou okna. Všimněte si univerzálnosti této rovnice. Stejná rovnice, jakou můžeme použít pro posouzení teplotního komfortu ve stavbě, dokáže modelovat například vliv stromu na tepelnou pohodu v městském prostředí nebo prostup tepla do dřeva při jeho tepelné modifikaci.
Shrnutí, hlavní myšlenky

- Aplikované vědy (fyzika, biologie, nauka o materiálu, hydrologie) přirozeně formulují své zákony a poznatky mimo jiné i kvantitativně a pomocí pojmů vyjadřujících rychlosti změn. Doteď jsme aparátem střední školy uměli počítat jenom průměrně rychlosti za daný časový interval, s derivací dostáváme do ruky nástroj pro práci s okamžitými rychlostmi.
- Jakmile ve slovním popisu procesu slyšíme slovo rychlost, znamená to, že při matematickém modelování hraje pravděpodobně důležitou roli derivace. Okamžitá rychlost je derivace. Jenom v krásných případech probíhajících konstantní rychlostí můžeme tuto rychlost počítat pomocí podílu, jak to známe u rychlosti pohybu.
- Naučili jsme se nebo se naučíme pomocí vzorců derivovat běžné funkce.
- Derivace umožní předpovědět, co se stane s veličinou, která závisí na jiné veličině a tato jiná veličina se mění známou rychlostí. Ze vztahu, který dává do souvislosti hodnoty dvou veličin, můžeme určit pomocí derivací vztah, dávající do souvislosti rychlosti změn těchto veličin.
- V případě nutnosti umíme rozšířit derivace i do světa funkcí více proměnných. Děláme to tak, že sledujeme rychlost změny způsobenou vždy změnou jenom jedné veličiny. Proto příslušné derivace nazýváme parciální. (Parciální znamená v tomto smyslu částečný.)