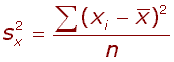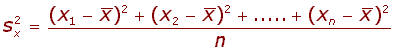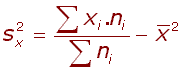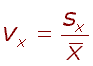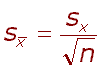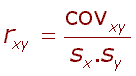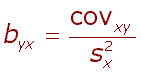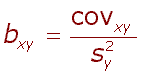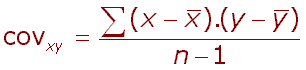Analýza kvantitativních vlastností

Změříme-li hodnotu nějaké kvantitativní vlastnosti organizmu, zjišťujeme jeho fenotypovou hodnotu, na jejímž základě lze odhadnout genotypovou hodnotu vlastnosti. Hodnotíme-li větší množství jednotlivých hodnot v populaci, lze popsat fenotypovou variabilitu a na jejím základě odhadnout variabilitu genotypovou.

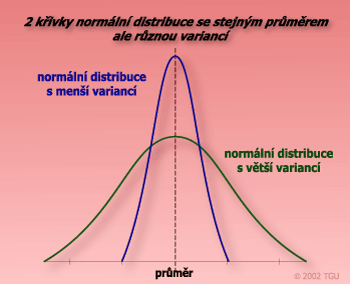
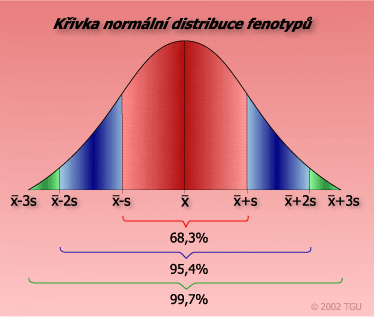
Distribuce fenotypů může být popsána různými způsoby. Jako první se určuje střed distribuce (průměr). Ten však sám o sobě nestačí k popisu distribuce. Je nutné určit variabilitu (pomocí variance, rozptylu) okolo tohoto průměru, která určuje tvar křivky distribuce.

Průměr, variance a směrodatná odchylka

Střed distribuce je aritmetickým průměrem všech fenotypových hodnot a je definován:

= průměr = součet všech hodnot = počet hodnot

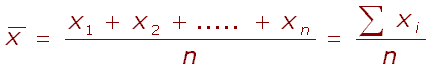Variabilita okolo průměru je definována jako součet čtverců odchylek od průměru:

výpočtový vzorec:

Směrodatná odchylka je další způsob hodnocení variability distribuce a navíc je v jednotkách měřené vlastnosti:   Variační koeficient vyjadřuje relativní míru variance. Pomocí něj, lze porovnávat variabilitu různých vlastností s různými jednotkami (na rozdíl od směrodatné odchylky):

Další doplňující mírou variance je střední chyba průměru (charakteristika přesnosti odhadu průměru, závislá na velikosti výběrového souboru):

Data jsou často sumarizována jako:

Kovariance, korelace a regrese

Genetické studie často sledují vztahy mezi různými vlastnostmi, nebo vztah mezi vlastností změřenou u rodičů a u potomků a pod. Na základě těchto vztahů jsou určovány různé genetické parametry (heritabilita, genetické korelace, plemenná hodnota, ...). Vznik závislosti mezi znaky může být podmíněn vazbou genů nebo pleiotropním účinkem. 

Existence vzájemného vztahu dvou vlastností x a y je korelace, jeho těsnost vyjadřuje koeficient korelace r (s rozmezím hodnot: -1 až + 1).
Jednoduchou závislost dvou vlastností x a y, kdy jedna vlastnost je závisle a druhá nezávisle proměnná, se nazývá regrese a jeho stupeň se vyjadřuje regresním koeficientem b. Ten je vyjádřen v jednotkách závisle proměnné.
Kovariance je analogická k varianci, ale zahrnuje současně odchylky od průměru obou vlastností zároveň (x a y), nebo-li součet součinů odchylek vlastností x a y.