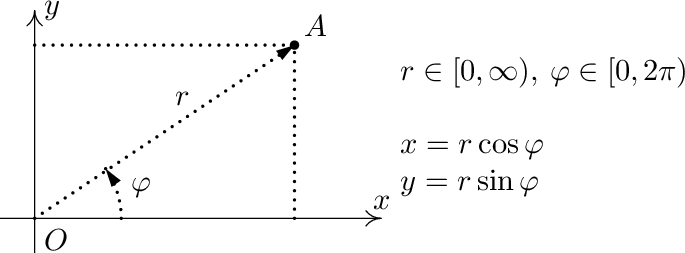4 Polární souřadnice
Dosud jsme používali pouze kartézské souřadnice: dvojici čísel udávající vzdálenost bodu od osy \( \displaystyle y\) a od osy \( \displaystyle x\), která jednoznačně určuje polohu bodu v rovině1 . V praxi je někdy výhodnější použít i jiný způsob jak pomocí dvojice čísel charakterizovat polohu bodu v rovině – takové souřadnice potom nazýváme křivočaré souřadnice.
Z křivočarých souřadnic jsou nejdůležitější polární souřadnice. Při jejich použití polohu bodu \( \displaystyle A\) zadáváme tak, že určíme vzdálenost \( \displaystyle r\) bodu od počátku soustavy souřadnic \( \displaystyle O\) a úhel \( \displaystyle \varphi \), který svírá spojnice bodů \( \displaystyle O\) a \( \displaystyle A\) s kladnou částí osy \( \displaystyle x\).
Chceme-li převést dvojný integrál do polárních
souřadnic, provádíme v něm vlastně substituci
\( \displaystyle x = r\cos \varphi \) a
\( \displaystyle y = r\sin \varphi \). Přitom se transformují
i diferenciály \( \displaystyle \, \mathrm{d}x\)
a \( \displaystyle \, \mathrm{d}y\) a
výsledný vzorec má tvar
| \[ \int\int _{\Omega }f(x,y)\, \mathrm{d}x\, \mathrm{d}y =\int\int _{\Omega }f(r\cos \varphi ,r\sin \varphi )\, \cdot r\, \mathrm{d}\varphi \, \mathrm{d}r. \] |
V diferenciálním počtu polární souřadnice používáme především tam, kde má problém radiální symetrii. Například při studiu ochlazování nebo kmitů kruhových desek či válcovitých součástek. V integrálním počtu tyto souřadnice použijeme zejména v případě, kdy integrujeme přes kružnici nebo její část (např. mezikruží či kruhová výseč). V takovém případě mají totiž integrály které vzniknou po aplikaci Fubiniovy věty pevné meze a výpočet druhého integrálu je zpravidla jednodušší. V následujícím příkladě pro srovnání vypočteme tentýž integrál v polárních i v kartézských souřadnicích.
Příklad 4.1. Vypočtěte \( \displaystyle \int\int _{\Omega }x\, \mathrm{d}x\, \mathrm{d}y\), kde \( \displaystyle \Omega \) je čtvrtina jednotkového kruhu, ležící v prvním kvadrantu.
![y
r ∈ (0,π1]
φ ∈ [0,2]
Ω
x](in-mat-web30x.png)
Výpočet v polárních souřadnicích:
\[ \begin{align*} \int\int _{\Omega }x\, \mathrm{d}x\, \mathrm{d}y & =\int _{ 0}^{1}{\Bigl (\int _{ 0}^{\pi ∕2}\underbrace{ \ r\cos \varphi \ }_{ \text{funkce}}\underbrace{r}_{\text{Jakobián}}\, \mathrm{d}\varphi \Bigr )}\, \mathrm{d}r =\int _{ 0}^{1}{\Bigl [r^{2}\sin \varphi \Bigr ]}_{ 0}^{\pi ∕2}\, \mathrm{d}r & & \\ & =\int _{ 0}^{1}{\Bigl [r^{2}\sin { \pi \over 2} - r\sin 0\Bigr ]}\, \mathrm{d}r =\int _{ 0}^{1}{\Bigl [r^{2}\Bigr ]}\, \mathrm{d}r & & \\ & ={\Bigl [{ r^{3} \over 3} \Bigr ]}_{0}^{1} ={ 1 \over 3} -{ 0 \over 3} ={ 1 \over 3} & & \\\end{align*}\]Výpočet v kartézských souřadnicích:
\[ \begin{align*} \int\int _{\Omega }x\, \mathrm{d}x\, \mathrm{d}y & =\int _{ 0}^{1}{\Bigl (\int _{ 0}^{\sqrt{1-x^{2}} }x\, \mathrm{d}y\Bigr )}\, \mathrm{d}x & & \\ & =\int _{ 0}^{1}{\Bigl [xy\Bigr ]}_{ 0}^{\sqrt{1-x^{2}} }\, \mathrm{d}x & & \\ & =\int _{ 0}^{1}x\sqrt{1 - x^{2}}\, \mathrm{d}x & & \\ & = \text{substituční metodou …} & & \\ & ={\Bigl [ -{ 1 \over 3} (1 - x^{2})^{{ 3 \over 2} }\Bigr ]}_{0}^{1} & & \\ & = -{ 1 \over 3} (0)^{{ 3 \over 2} } -{\Bigl (-{ 1 \over 3} (1)^{{ 3 \over 2} }\Bigr )} & & \\ & ={ 1 \over 3} & & \\\end{align*}\]