Dvojny integral v obecne oblasti

3 Dvojný integrál v obecné oblasti

Definice 3.1 (dvojný integrál v obecné oblasti). Buď \( \displaystyle \Omega \) uzavřená ohraničená oblast. Buď \( \displaystyle R\) dostatečně velký obdélník, takový, že \( \displaystyle \Omega \subseteq R\). Definujme na \( \displaystyle R\) funkci \( \displaystyle g\) předpisem

\[ g(x,y) = \left \{\array{ f(x,y)\quad & (x,y)\in \Omega \cr 0 \quad & \text{jinak}} \right . \]

Potom definujeme integrál funkce \( \displaystyle f\) na množině \( \displaystyle \Omega \) předpisem

\[ \int\int _{\Omega }f(x,y)\, \mathrm{d}x\, \mathrm{d}y =\int\int _{R}g(x,y)\, \mathrm{d}x\, \mathrm{d}y. \]

V dalším budeme pro jednoduchost předpokládat, že oblasti přes které integrujeme mají hranici tvořenu po částech hladkou uzavřenou křivkou.

y

ψ(x)

oblast Ω

φ(x)
a b x

Věta 3.1 (Fubini). Nechť \( \displaystyle f\) je funkce spojitá v uzavřené oblasti

\[ \Omega = \{(x,y)\in \mathbb{R}^{2} : a\leq x\leq b\text{ a }\varphi (x)\leq y\leq \psi (x)\}. \]

Potom

\[ \int\int _{\Omega }f(x,y)\, \mathrm{d}x\, \mathrm{d}y = \int _{a}^{b}{\Bigl [\int _{ \varphi (x)}^{\psi (x)}f(x,y)\, \mathrm{d}y\Bigr ]}\, \mathrm{d}x \]

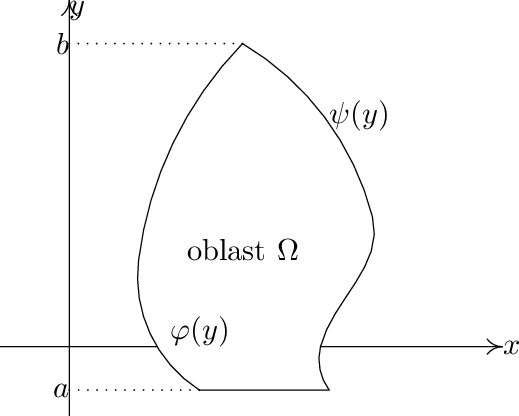
y

b
ψ (y)

oblast Ω

φ (y)
x
a

Věta 3.2 (Fubini). Nechť \( \displaystyle f\) je funkce spojitá v uzavřené oblasti

\[ \Omega = \{(x,y)\in \mathbb{R}^{2} : a\leq y\leq b\text{ a }\varphi (y)\leq x\leq \psi (y)\}. \]

Potom

\[ \int\int _{\Omega }f(x,y)\, \mathrm{d}x\, \mathrm{d}y = \int _{a}^{b}{\Bigl [\int _{ \varphi (y)}^{\psi (y)}f(x,y)\, \mathrm{d}x\Bigr ]}\, \mathrm{d}y \]

Příklad 3.1.

Vypočtěte \( \displaystyle \int\int _{\Omega }2y\, \mathrm{d}x\, \mathrm{d}y\) přes množinu vyznačenou na obrázku.

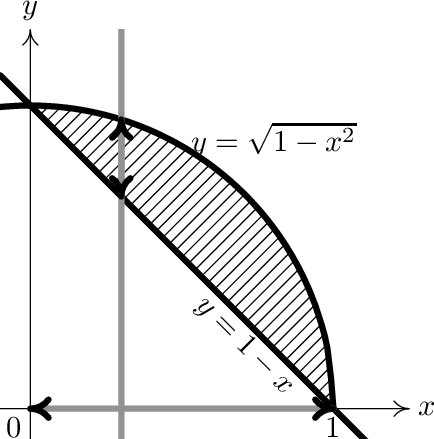
y

√------
y = 1 - x2

y = 1- x

x
0 1

\( \displaystyle x_{\mathop{min}} = 0\),

\( \displaystyle x_{\mathop{max}} = 1\),

\( \displaystyle y_{\mathop{min}} = 1 - x\),

\( \displaystyle y_{\mathop{max}} = \sqrt{1 - x^{2}}\)

\[ \begin{align*} \int\int _{\Omega }2y\, \mathrm{d}x\, \mathrm{d}y & =\int _{ 0}^{1}{\Bigl (\int _{ 1-x}^{\sqrt{1-x^{2}} }2y\, \mathrm{d}y\Bigr )}\, \mathrm{d}x & & \\ & =\int _{ 0}^{1}{\Bigl ({\Bigl [y^{2}\Bigr ]}_{ 1-x}^{\sqrt{1-x^{2}} }\Bigr )}\, \mathrm{d}x & & \\ & =\int _{ 0}^{1}{\Bigl ({\Bigl [1 - x^{2} - (1 - x)^{2}\Bigr ]}\Bigr )}\, \mathrm{d}x & & \\ & =\int _{ 0}^{1}{\Bigl (1 - x^{2} - (1 - 2x + x^{2})\Bigr )}\, \mathrm{d}x & & \\ & =\int _{ 0}^{1}{\Bigl (2x - 2x^{2}\Bigr )}\, \mathrm{d}x & & \\ & ={\Bigl [ x^{2} -{ 2 \over 3} x^{3}\Bigr ]}_{ 0}^{1} & & \\ & = 1 -{ 2 \over 3} ={ 1 \over 3} & & \\\end{align*}\]

Věta 3.3 (linearita integrálu). Buď \( \displaystyle f_{1}\), \( \displaystyle f_{2}\) funkce integrovatelné v \( \displaystyle \Omega \) a \( \displaystyle c_{1}\), \( \displaystyle c_{2}\) libovolná reálná čísla. Platí

\[ \int\int _{\Omega }{\bigl [c_{1}f_{1}(x,y) + c_{2}f_{2}(x,y)\bigr ]}\, \mathrm{d}x\, \mathrm{d}y = c_{1}\int\int _{\Omega }f_{1}(x,y)\, \mathrm{d}x\, \mathrm{d}y + c_{2}\int\int _{\Omega }f_{2}(x,y)\, \mathrm{d}x\, \mathrm{d}y \]

Věta 3.4 (aditivita vzhledem k oboru integrace). Nechť je oblast \( \displaystyle \Omega \) rozdělena na dvě oblasti \( \displaystyle \Omega _{1}\) a \( \displaystyle \Omega _{2}\), které mají společné nejvýše hraniční body. Platí

\[ \int\int _{\Omega }f(x,y)\, \mathrm{d}x\, \mathrm{d}y =\int\int _{\Omega _{1}}f(x,y)\, \mathrm{d}x\, \mathrm{d}y +\int\int _{\Omega _{2}}f(x,y)\, \mathrm{d}x\, \mathrm{d}y \]