2 Dvojný integrál na obdélníku
Definujme funkci na obdélníku \( \displaystyle R = [a,b]\times [c,d]\) ohraničenou funkci \( \displaystyle f(x,y)\). Obdélník rozdělme na podobdélníky \( \displaystyle p_{1}\), \( \displaystyle p_{2}\), …, \( \displaystyle p_{n}\) o obsazích \( \displaystyle \Delta p_{1}\), \( \displaystyle \Delta p_{2}\), …, \( \displaystyle \Delta p_{n}\). Toto dělení označme \( \displaystyle D\).
V obdélníčku \( \displaystyle p_{i}\)
najdeme supremum \( \displaystyle M_{i}\)
a infimum \( \displaystyle m_{i}\)
funkce \( \displaystyle f(x,y)\).
Sestrojme horní a dolní integrální součet příslušný
dělení \( \displaystyle D\)
podle vzorců
- Supremum množiny všech dolních součtů nazýváme dolní dvojný integrál a značíme \( \displaystyle \underline{\int\int _{R}}f(x,y)\, \mathrm{d}x\, \mathrm{d}y\).
- Infimum množiny všech horních součtů nazýváme horní dvojný integrál a značíme \( \displaystyle \overline{\int\int _{R}}f(x,y)\, \mathrm{d}x\, \mathrm{d}y\).
Definice 2.1 (dvojný integrál). Jestliže jsou si horní a dolní integrál rovny, pak jejich společnou hodnotu značíme
| \[ \int\int _{R}f(x,y)\, \mathrm{d}x\, \mathrm{d}y \] | (2.1) |
a nazýváme dvojný integrál funkce \( \displaystyle f\) v \( \displaystyle R\). O funkci \( \displaystyle f\) říkáme, že je na množině \( \displaystyle R\) integrovatelná.
Výpočet dvojného integrálu provádíme s využitím následující věty o převodu dvojného integrálu na dvojnásobný (dva ”obyčejné” integrály).
Věta 2.1 (Fubini). Nechť \( \displaystyle R = [a,b]\times [c,d]\) je
uzavřený obdélník v \( \displaystyle \mathbb{R}^{2}\)
a \( \displaystyle f\) funkce definovaná
a spojitá na \( \displaystyle R\).
Pak platí
| \[ \int\int _{R}f(x,y)\, \mathrm{d}x\, \mathrm{d}y =\int _{ a}^{b}{\Bigl [\int _{ c}^{d}f(x,y)\, \mathrm{d}y\Bigr ]}\, \mathrm{d}x =\int _{ c}^{d}{\Bigl [\int _{ a}^{b}f(x,y)\, \mathrm{d}x\Bigr ]}\, \mathrm{d}y. \] |
Příklad 2.1. Vypočtěte
\( \displaystyle \int\int _{\Omega }(x + y)\, \mathrm{d}x\, \mathrm{d}y\)
přes obdélník vyznačený na obrázku.
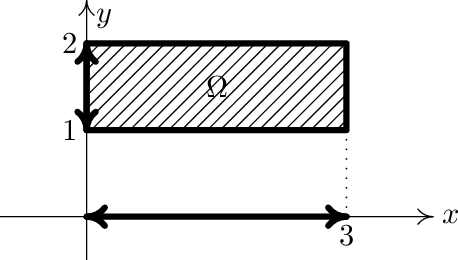
\[ \begin{align*} \int\int _{\Omega }(x + y)\, \mathrm{d}x\, \mathrm{d}y & = \int _{1}^{2}{\Bigl [\int _{ 0}^{3}(x + y)\, \mathrm{d}x\Bigr ]}\, \mathrm{d}y =\int _{ 1}^{2}{\Bigl [{ x^{2} \over 2} + xy\Bigr ]}_{0}^{3}\, \mathrm{d}y & & \\ & =\int _{ 1}^{2}{\Bigl [{ 9 \over 2} + 3y -{\bigl ({ 0 \over 2} + 0y\bigr )}\Bigr ]}\, \mathrm{d}y =\int _{ 1}^{2}{\Bigl ({ 9 \over 2} + 3y\Bigr )}\, \mathrm{d}y & & \\ & ={\Bigl [{ 9 \over 2} y + 3{ y^{2} \over 2} \Bigr ]}_{1}^{2} ={ 9 \over 2} \cdot 2 + 3\cdot { 4 \over 2} -{\Bigl ({ 9 \over 2} + 3\cdot { 1 \over 2} \Bigr )} & & \\ & = 9 + 6 - 6 = 9 & & \\\end{align*}\]
Věta 2.2 (Důsledek Fubiniovy věty). Platí-li ve větě 2.1 rovnost \( \displaystyle f(x,y) = g(x)h(y)\), platí
| \[ \int\int _{R}f(x,y)\, \mathrm{d}x\, \mathrm{d}y =\int _{ a}^{b}g(x)\, \mathrm{d}x\int _{ c}^{d}h(y)\, \mathrm{d}y. \] |