3 Stacionární body
Poznámka 3.1 (klasifikace stacionárních bodů). 
Podle chování
trajektorií v okolí stacionárních bodů rozdělujeme tyto
stacionární body do několika navzájem disjunktních skupin. Nechť
\( \displaystyle (x^{*},y^{*})\) je
singulárním bodem systému (1.1).
- Uzel
- Stacionární bod \( \displaystyle (x^{*},y^{*})\) se nazývá uzel, jestliže všechny trajektorie \( \displaystyle (x(t),y(t))\) z nějakého okolí tohoto bodu konvergují pro \( \displaystyle t\to \infty \) nebo \( \displaystyle t\to -\infty \) k \( \displaystyle (x^{*},y^{*})\) tak, že nedochází k oscilacím kolem limitní hodnoty.
- Ohnisko
- Stacionární bod \( \displaystyle (x^{*},y^{*})\) se nazývá ohnisko, jestliže všechny trajektorie z nějakého okolí tohoto stacionární bodu do tohoto bodu konvergují buď pro \( \displaystyle t\to \infty \) nebo pro \( \displaystyle t\to -\infty \) a to tak, že kolem tohoto bodu oscilují se zmenšující se amplitudou.
- Sedlo
- Stacionární bod \( \displaystyle (x^{*},y^{*})\) se nazývá sedlo, jestliže v každém jeho okolí existuje pouze konečný počet trajektorií, které pro \( \displaystyle t\to \pm \infty \) konvergují k tomuto bodu.
- Střed a bod rotace
- Stacionární bod \( \displaystyle (x^{*},y^{*})\) se nazývá bod rotace, jestliže každé jeho okolí obsahuje nekonečně mnoho trajektorií, které jsou cykly. Pokud v nějakém okolí existují pouze cykly, nazývá se tento bod navíc střed.
- Uzel nebo ohnisko nazýváme stabilní, jestliže všechny trajektorie do něj konvergují pro \( \displaystyle t\to \infty \), tj. všechny trajektorie z nějakého okolí směřují do tohoto bodu. V opačném případě tento bod nazýváme nestabilní.
- Pro stabilní uzel a ohnisko existují oblasti ve fázové rovině které mají tu vlastnost, že všechny trajektorie procházející některou z těchto oblastí konvergují pro \( \displaystyle t\to \infty \) do tohoto stacionárního bodu. Takové oblasti se nazývají oblasti atraktivity stacionárního bodu.
Definice 3.1 (Jacobiho matice). Matice
| \[ J(x,y) = \left (\array{ { \partial\, f \over \partial\, x} (x,y)& { \partial\, f \over \partial\, y} (x,y) \cr { \partial\, g \over \partial\, x} (x,y)& { \partial\, g \over \partial\, y} (x,y) \cr } \right ) \] |
se nazývá Jacobiho matice soustavy (1.1).
Definice 3.2. Charakteristickou rovnicí matice \( \displaystyle A\) rozumíme kvadratickou rovnici \( \displaystyle \det (A -\lambda I) = 0\) s neznámou \( \displaystyle \lambda \), tj. charakteristickou rovnicí matice \( \displaystyle A = \left (\array{ a& b\cr c& d} \right )\) je rovnice
| \[ \lambda ^{2} - (a + d)\lambda + ad - bc = 0. \] |
Kořeny této rovnice (reálné nebo komplexní) nazýváme vlastní čísla matice \( \displaystyle A\).
Věta 3.1 (klasifikace stacionárních bodů pomocí vlastních čísel Jacobiho matice).
Předpokládejme, že nula není vlastním číslem Jacobiho matice pro
dvourozměrný autonomní systém (1.1).
- Jsou-li obě vlastní čísla reálná kladná, je stacionární bod nestabilní uzel.
- Jsou-li obě vlastní čísla reálná záporná, je stacionární bod stabilní uzel.
- Jsou-li vlastní čísla reálná a mají-li opačná znaménka, je stacionární bod sedlo.
- Jsou-li vlastní čísla komplexně sdružená s kladnou reálnou částí, je stacionární bod nestabilní ohnisko.
- Jsou-li vlastní čísla komplexně sdružená se zápornou reálnou částí, je stacionární bod stabilní ohnisko.
- Jsou-li vlastní čísla komplexně sdružená s nulovou reálnou částí, je stacionární bod ohnisko nebo bod rotace.
Vlastní hodnoty, \( \displaystyle \lambda _{1,2}\in \mathbb{R}\) | typ stac. bodu | průběh trajektorií |
\( \displaystyle \lambda _{1}\geq \lambda _{2} > 0\) | nestabilní uzel |  |
\( \displaystyle \lambda _{1} > 0 >\lambda _{2}\) | sedlo |  |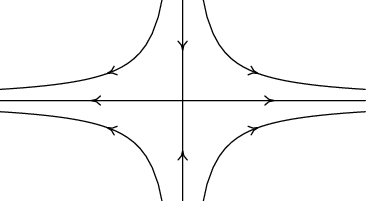
\( \displaystyle 0 >\lambda _{1}\geq \lambda _{2}\) | stabilní uzel |  |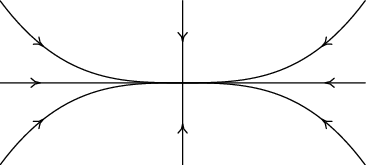
Vlastní hodnoty, \( \displaystyle \lambda _{1,2}\not \in \mathbb{R}\) | typ stac. bodu | průběh trajektorií |
\( \displaystyle ℜ(\lambda _{1,2}) > 0\) | nestabilní ohnisko |  |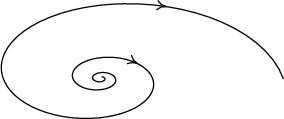
\( \displaystyle ℜ(\lambda _{1,2}) < 0\) | stabilní ohnisko |  |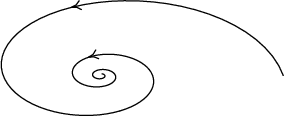
\( \displaystyle ℜ(\lambda _{1,2}) = 0\) | ohnisko nebo bod rotace | 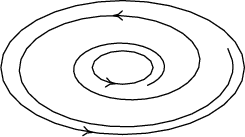 nebo kterákoliv z předchozích možností |
Poznámka 3.2. Zjednodušeně řečeno, kdykoliv se mezi vlastními hodnotami Jacobiho matice v bodě \( \displaystyle S\) objeví vlastní hodnota se zápornou reálnou částí, existuje trajektorie konvergující do bodu \( \displaystyle S\). Pokud má některé vlastní hodnota kladnou reálnou část, existuje trajektorie vycházející z bodu \( \displaystyle S\). Pokud mají vlastní hodnoty nenulovou imaginární část, dochází v okolí bodu \( \displaystyle S\) k oscilacím.
Jiná možnost, jak určit typ stacionárních bodů, je obsažena v následující větě. V této větě \( \displaystyle D\) značí determinant Jacobiho matice v bodě \( \displaystyle (x^{*},y^{*})\), tj. a \( \displaystyle \Delta \) stopu1 Jacobiho matice v tomto bodě, tj.
\[ \begin{align*} D & =\det J(x^{*},y^{*}) ={ \partial\, f \over \partial\, x} (x^{*},y^{*}){ \partial\, g \over \partial\, y} (x^{*},y^{*}) -{ \partial\, f \over \partial\, y} (x^{*},y^{*}){ \partial\, g \over \partial\, x} (x^{*},y^{*}), & & \\\Delta & =\mathop{\mathrm{Tr}} J(x^{*},y^{*}) ={ \partial\, f \over \partial\, x} (x^{*},y^{*}) +{ \partial\, g \over \partial\, y} (x^{*},y^{*}). & & \\\end{align*}\]Věta 3.2. Nechť \( \displaystyle (x^{*},y^{*})\) je stacionární bod soustavy (1.1) a \( \displaystyle J(x^{*},y^{*})\) hodnota Jacobiho matice v tomto bodě. Pomocí čísel \( \displaystyle D\) a \( \displaystyle \Delta \) lze rozhodnout o kvalitě stacionárního bodu \( \displaystyle (x^{*},y^{*})\) podle následující tabulky.
| \( \displaystyle D^{} < 0\) | sedlo | ||
| \( \displaystyle D > 0\) | \( \displaystyle \Delta > 0\) | \( \displaystyle \Delta ^{2}\geq 4D\) | nestabilní uzel |
| \( \displaystyle \Delta ^{2} < 4D\) | nestabilní ohnisko | ||
| \( \displaystyle \Delta < 0\) | \( \displaystyle \Delta ^{2}\geq 4D\) | stabilní uzel | |
| \( \displaystyle \Delta ^{2} < 4D\) | stabilní ohnisko | ||
| \( \displaystyle \Delta ^{} = 0\) | bod rotace nebo ohnisko | ||