2 Určitý integrál
Definice 2.1 (dělení intervalu). Buď \( \displaystyle [a,b]\) uzavřený interval \( \displaystyle -\infty < a < b <\infty \) . Dělením intervalu \( \displaystyle [a,b]\) rozumíme konečnou posloupnost \( \displaystyle D = \{x_{0},x_{1},\mathop{\mathop{…}},x_{n}\}\) bodů z intervalu \( \displaystyle [a,b]\) s vlastností
| \[ a = x_{0} < x_{1} < x_{2} < x_{3} <\cdots < x_{n-1} < x_{n} = b. \] |
Čísla \( \displaystyle x_{i}\) nazýváme dělící body.
- Dolní závorou intervalu \( \displaystyle (0,1)\) jsou například čísla \( \displaystyle - 1,-\pi ,0\) .
- Dolní závorou intervalu \( \displaystyle (0,1)\) nejsou čísla \( \displaystyle \frac{1} {2}\) , \( \displaystyle 6\) ani \( \displaystyle e\) .
Příklad 2.2. Intervaly \( \displaystyle (0,1)\) , \( \displaystyle [0,1]\) , \( \displaystyle (0,1]\) mají všechny infimum rovno číslu \( \displaystyle 0\) .
Příklad 2.3. Intervaly \( \displaystyle (0,1)\) , \( \displaystyle [0,1]\) , \( \displaystyle (0,1]\) mají všechny supremum rovno číslu \( \displaystyle 1\) .
Definice 2.6 (dolní a horní součet). Buď \( \displaystyle [a,b]\) uzavřený interval a \( \displaystyle f\) funkce definovaná, spojitá1 a ohraničená na \( \displaystyle [a,b]\) . Buď \( \displaystyle D\) dělení intervalu \( \displaystyle [a,b]\) . Buď \( \displaystyle s_{i} =\mathop{ min}\{f(x),x_{i-1}\leq \xi _{i}\leq x_{i}\}\) pro \( \displaystyle i = 1..n\) minimum funkce \( \displaystyle f\) na jednotlivých intervalech dělení. Potom součet
| \[ s(f,D) =\sum _{ i=1}^{n}s_{ i}(x_{i} - x_{i-1}) \] |
se nazývá dolní součet funkce \( \displaystyle f\) příslušný dělení \( \displaystyle D\) . Podobně obdržíme horní součet funkce \( \displaystyle f\) , pokud použijeme \( \displaystyle S_{i} =\mathop{ min}\{f(x),x_{i-1}\leq \xi _{i}\leq x_{i}\}\) a
| \[ S(f,D) =\sum _{ i=1}^{n}S_{ i}(x_{i} - x_{i-1}). \] |
Definice 2.7 (určitý integrál). Buď \( \displaystyle [a,b]\) uzavřený interval a \( \displaystyle f\) funkce definovaná, spojitá a ohraničená na \( \displaystyle [a,b]\) a \( \displaystyle \mathcal D\) množina všech dělení intervalu \( \displaystyle [a,b]\) . Řekneme, že funkce \( \displaystyle f\) je integrovatelná na intervalu \( \displaystyle [a,b]\) , jestliže existuje číslo \( \displaystyle I\in \mathbb{R}\) s vlastností
| \[ I =\mathop{ sup}_{D\in \mathcal D}s(f,D) =\mathop{ inf} _{D\in \mathcal D}S(f,D), \] |
pak číslo \( \displaystyle I\) nazýváme určitý integrál funkce \( \displaystyle f\) na intervalu \( \displaystyle [a,b]\) a označujeme
| \[ \int _{a}^{b}f(x)\, \mathrm{d}x. \] |
Následující definice doplňuje definici určitého integrálu v případě, že dolní mez není menší než mez horní.
Věta 2.1 (linearita určitého integrálu vzhledem k funkci). Nechť \( \displaystyle f\) , \( \displaystyle g\) jsou funkce integrovatelné na \( \displaystyle [a,b]\) , \( \displaystyle c\) nechť je reálné číslo. Pak platí
\[ \begin{align*} \int _{a}^{b}[f(x) + g(x)]\, \mathrm{d}x & =\int _{ a}^{b}f(x)\, \mathrm{d}x +\int _{ a}^{b}g(x)\, \mathrm{d}x, & & \\\int _{a}^{b}cf(x)\, \mathrm{d}x & = c\int _{ a}^{b}f(x)\, \mathrm{d}x. & & \\\end{align*}\]Věta 2.2 (aditivita určitého integrálu vzhledem k mezím). Nechť \( \displaystyle f\) je funkce integrovatelná na \( \displaystyle [a,b]\) . Buď \( \displaystyle c\in (a,b)\) libovolné. Pak je \( \displaystyle f\) integrovatelná na intervalech \( \displaystyle [a,c]\) a \( \displaystyle [c,b]\) a platí
| \[ \int _{a}^{b}f(x)\, \mathrm{d}x =\int _{ a}^{c}f(x)\, \mathrm{d}x +\int _{ c}^{b}f(x)\, \mathrm{d}x. \] |
Věta 2.3 (monotonie vzhledem k funkci). Buďte \( \displaystyle f\) a \( \displaystyle g\) funkce integrovatelné na \( \displaystyle [a,b]\) takové, že \( \displaystyle f(x)\leq g(x)\) pro \( \displaystyle x\in (a,b)\) . Pak platí \( \displaystyle \int _{a}^{b}f(x)\, \mathrm{d}x\leq \int _{a}^{b}g(x)\, \mathrm{d}x.\)
Poznámka 2.1 (integrál z nezáporné funkce). Pro \( \displaystyle f\equiv 0\) dostáváme z předchozí věty tvrzení, že integrál z funkce nezáporné na celém integračním oboru je nezáporný.
V praxi se určitý integrál počítá užitím následující věty.
Věta 2.4 (Newtonova–Leibnizova věta). 
Nechť funkce
\( \displaystyle f(x)\) je Riemannovsky
integrovatelná na \( \displaystyle [a,b]\) .
Nechť \( \displaystyle F(x)\) je funkce
spojitá na \( \displaystyle [a,b]\) ,
která je intervalu \( \displaystyle (a,b)\)
primitivní k funkci \( \displaystyle f(x)\) .
Pak platí
| \[ \int _{a}^{b}f(x)\, \mathrm{d}x = [F(x)]_{ a}^{b} = F(b) - F(a). \] |
Příklad 2.4 (použití Newtonovy–Leibnizovy věty). Protože primitivní funkcí k funkci \( \displaystyle x^{3}\) je funkce \( \displaystyle \frac{x^{4}} {4} \) , platí
| \[ \int _{0}^{1}x^{3}\, \mathrm{d}x = \left [\frac{x^{4}} {4} \right ]_{0}^{1} = \frac{1^{4}} {4} -\frac{0^{4}} {4} = \frac{1} {4}. \] |
V následující poznámce si uvedeme metodu, jak přibližně určit hodnotu určitého integrálu v případě, že není snadné použít Newtonovu–Leibnizovu větu, např. když nedokážeme nalézt primitivní funkci.
Poznámka 2.2 (lichoběžníkové pravidlo, přibližný výpočet určitého integrálu
).
Nechť je funkce \( \displaystyle f\)
spojitá na intervalu \( \displaystyle [a,b]\) .
Rozdělme interval \( \displaystyle [a,b]\)
na \( \displaystyle n\) intervalů
stejné délky \( \displaystyle h\) ,
tj. platí \( \displaystyle h = \frac{b-a}
{n} \) .
Krajní body těchto intervalů označme po řadě
\( \displaystyle x_{0}\) ,
\( \displaystyle x_{1}\) , …,
\( \displaystyle x_{n}\)
a jim odpovídající funkční hodnoty
\( \displaystyle y_{0}\) ,
\( \displaystyle y_{1}\) , …,
\( \displaystyle y_{n}\) .
Hlavní myšlenka aproximace integrálu funkce
\( \displaystyle f\) na
intervalu \( \displaystyle [a,b]\)
spočívá v tom, že na tomto intervalu nahradíme funkci
\( \displaystyle f(x)\) lomenou čarou
s vrcholy v bodech \( \displaystyle [a = x_{0},y_{0}]\) ,
\( \displaystyle [x_{1},y_{1}]\) ,
…\( \displaystyle [x_{n} = b,y_{n}]\)
a integrál z takto upravené funkce vypočteme jako součet
obsahů jednotlivých lichoběžníků, z nichž je obrazec
pod lomenou čárou sestaven. (Toto lze provést i když funkce
\( \displaystyle f\) nezachovává
znaménko na intervalu \( \displaystyle [a,b]\) .)
Potom platí:
| \[ \int _{a}^{b}f(x)\, \mathrm{d}x\approx \frac{h} {2}{\Bigl (y_{0} + 2y_{1} + 2y_{2} +\cdots +2y_{n-1} + y_{n}\Bigr )}. \] |
Přitom chyba v tomto vzorci je tím menší, čím je
- větší \( \displaystyle n\) ,
- menší rozdíl \( \displaystyle b - a\) ,
- menší \( \displaystyle |f''(x)|\) na \( \displaystyle (a,b)\) .
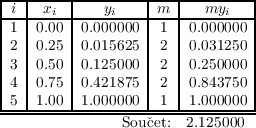
Příklad 2.5 (lichoběžníkové pravidlo). Pokusíme se pomocí lichoběžníkového pravidla aproximovat integrál \( \displaystyle \int _{0}^{1}x^{3}\, \mathrm{d}x\) z Příkladu 2.4. Rozdělíme interval \( \displaystyle [0,1]\) na 4 dílky o délce \( \displaystyle 0.25\) a pro pohodlný výpočet použijeme Tabulku 2.1.
Výsledná aproximace tedy je \( \displaystyle \int _{0}^{1}x^{3}\, \mathrm{d}x\approx \frac{0.25} {2} 2.125000 = 0.265526\) . Porovnáme-li tuto hodnotu s přesným výsledkem z Příkladu 2.4 vidíme, že přes poměrně primitivní aproximaci, je chyba menší než 7%. Jemnějším dělením získáme hodnotu ještě přesněji.
Pomocí integrálu můžeme definovat užitečné neelementární funkce – například primitivní funkce k funkcím, které jsme doposud neuměli integrovat. Umožní nám to následující věta.
Věta 2.5 (integrál jako funkce horní meze). Nechť funkce \( \displaystyle f(x)\) je spojitá na intervalu \( \displaystyle I\) a nechť \( \displaystyle a\in I\) . Potom funkce \( \displaystyle F(x)\) definovaná na \( \displaystyle I\) vztahem
| \[ F(x) =\int _{ a}^{x}f(t)\, \mathrm{d}t \] |
má na intervalu \( \displaystyle I\) derivaci a platí \( \displaystyle F'(x) = f(x)\) .
Příklad 2.6. Pro funkci \( \displaystyle f(x) = x^{2}\) platí \( \displaystyle \int _{0}^{x}t^{2}\, \mathrm{d}t = \left [\frac{t^{3}} {3} \right ]_{0}^{x} = \frac{x^{3}} {3} \) což je skutečně jedna z primitivních funkcí k funkci \( \displaystyle x^{2}\) , jak již víme z kapitoly o neurčitém integrálu (viz též vzorce na konci tohoto textu).
Poznámka 2.3. Již dříve jsme uvedli, že k funkci \( \displaystyle e^{-x^{2} }\) existuje primitivní funkce, ale tuto funkci neumíme najít. Nyní vidíme, že tuto primitivní funkci lze zapsat například ve tvaru \( \displaystyle \int _{0}^{x}e^{-t^{2} }\, \mathrm{d}t\) . Pokud nás zajímá například funkční hodnota v bodě \( \displaystyle x = 1\) , stačí určit hodnotu integrálu \( \displaystyle \int _{0}^{1}e^{-x^{2} }\, \mathrm{d}x\) . Tuto hodnotu sice neumíme vypočítat přesně, můžeme ji však přibližně vypočítat pomocí lichoběžníkového pravidla.
