3 Dvojný integrál
3.1 Dvojný integrál na obdélníku
Definujme funkci na obdélníku \( \displaystyle R = [a,b]\times [c,d]\) ohraničenou funkci \( \displaystyle f(x,y)\) . Obdélník rozdělme na podobdélníky \( \displaystyle p_{1}\) , \( \displaystyle p_{2}\) , …, \( \displaystyle p_{n}\) o obsazích \( \displaystyle \Delta p_{1}\) , \( \displaystyle \Delta p_{2}\) , …, \( \displaystyle \Delta p_{n}\) . Toto dělení označme \( \displaystyle D\) .
V obdélníčku \( \displaystyle p_{i}\)
najdeme supremum \( \displaystyle M_{i}\)
a infimum \( \displaystyle m_{i}\)
funkce \( \displaystyle f(x,y)\) .
Sestrojme horní a dolní integrální součet příslušný
dělení \( \displaystyle D\)
podle vzorců
- Supremum množiny všech dolních součtů nazýváme dolní dvojný integrál.
- Infimum množiny všech horních součtů nazýváme horní dvojný integrál .
Definice 3.1 (dvojný integrál). Jestliže jsou si horní a dolní integrál rovny, pak jejich společnou hodnotu značíme
| \[ \int\int _{R}f(x,y)\, \mathrm{d}x\, \mathrm{d}y \] | (3.1) |
a nazýváme dvojný integrál funkce \( \displaystyle f\) v \( \displaystyle R\) . O funkci \( \displaystyle f\) říkáme, že je na množině \( \displaystyle R\) integrovatelná.
Výpočet dvojného integrálu provádíme s využitím následující věty o převodu dvojného integrálu na dvojnásobný (dva ”obyčejné” integrály).
Věta 3.1 (Fubini). Nechť \( \displaystyle R = [a,b]\times [c,d]\) je
uzavřený obdélník v \( \displaystyle \mathbb{R}^{2}\)
a \( \displaystyle f\) funkce definovaná
a spojitá na \( \displaystyle R\) .
Pak platí
| \[ \int\int _{R}f(x,y)\, \mathrm{d}x\, \mathrm{d}y =\int _{ a}^{b}{\Bigl [\int _{ c}^{d}f(x,y)\, \mathrm{d}y\Bigr ]}\, \mathrm{d}x =\int _{ c}^{d}{\Bigl [\int _{ a}^{b}f(x,y)\, \mathrm{d}x\Bigr ]}\, \mathrm{d}y. \] |
Věta 3.2 (Důsledek Fubiniovy věty). Platí-li ve větě 3.1 rovnost \( \displaystyle f(x,y) = g(x)h(y)\) , platí
| \[ \int\int _{R}f(x,y)\, \mathrm{d}x\, \mathrm{d}y =\int _{ a}^{b}g(x)\, \mathrm{d}x\int _{ c}^{d}h(y)\, \mathrm{d}y. \] |
3.2 Dvojný integrál v obecné oblasti
Definice 3.2 (dvojný integrál v obecné oblasti). Buď \( \displaystyle \Omega \) uzavřená ohraničená oblast. Buď \( \displaystyle R\) dostatečně velký obdélník, takový, že \( \displaystyle \Omega \subseteq R\) . Definujme na \( \displaystyle R\) funkci \( \displaystyle g\) předpisem
| \[ g(x,y) = \left \{\array{ f(x,y)\quad & (x,y)\in \Omega \cr 0 \quad & \text{jinak}} \right . \] |
Potom definujeme integrál funkce \( \displaystyle f\) na množině \( \displaystyle \Omega \) předpisem
| \[ \int\int _{\Omega }f(x,y)\, \mathrm{d}x\, \mathrm{d}y =\int\int _{R}g(x,y)\, \mathrm{d}x\, \mathrm{d}y. \] |
V dalším budeme pro jednoduchost předpokládat, že oblasti přes které integrujeme mají hranici tvořenu po částech hladkou uzavřenou křivkou.
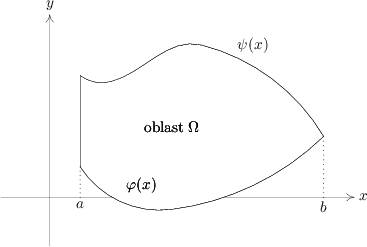
Věta 3.3 (Fubini). Nechť \( \displaystyle f\)
je funkce spojitá v uzavřené oblasti
| \[ \Omega = \{(x,y)\in \mathbb{R}^{2} : a\leq x\leq b\text{ a }\varphi (x)\leq y\leq \psi (x)\}. \] |
Potom
| \[ \int\int _{\Omega }f(x,y)\, \mathrm{d}x\, \mathrm{d}y = \int _{a}^{b}{\Bigl [\int _{ \varphi (x)}^{\psi (x)}f(x,y)\, \mathrm{d}y\Bigr ]}\, \mathrm{d}x \] |
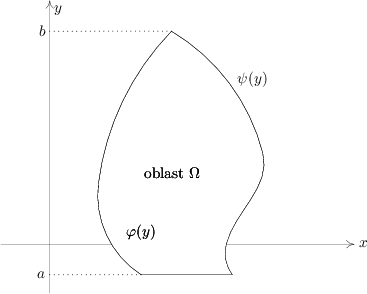
Věta 3.4 (Fubini). Nechť \( \displaystyle f\)
je funkce spojitá v uzavřené oblasti
| \[ \Omega = \{(x,y)\in \mathbb{R}^{2} : a\leq y\leq b\text{ a }\varphi (y)\leq x\leq \psi (y)\}. \] |
Potom
| \[ \int\int _{\Omega }f(x,y)\, \mathrm{d}x\, \mathrm{d}y = \int _{a}^{b}{\Bigl [\int _{ \varphi (y)}^{\psi (y)}f(x,y)\, \mathrm{d}x\Bigr ]}\, \mathrm{d}y \] |
Věta 3.5 (linearita integrálu). Buď
\( \displaystyle f_{1}\) ,
\( \displaystyle f_{2}\) funkce
integrovatelné v \( \displaystyle \Omega \)
a \( \displaystyle c_{1}\) ,
\( \displaystyle c_{2}\)
libovolná reálná čísla. Platí
| \[ \int\int _{\Omega }{\bigl [c_{1}f_{1}(x,y) + c_{2}f_{2}(x,y)\bigr ]}\, \mathrm{d}x\, \mathrm{d}y = c_{1}\int\int _{\Omega }f_{1}(x,y)\, \mathrm{d}x\, \mathrm{d}y + c_{2}\int\int _{\Omega }f_{2}(x,y)\, \mathrm{d}x\, \mathrm{d}y \] |
Věta 3.6 (aditivita vzhledem k oboru integrace). Nechť je oblast \( \displaystyle \Omega \) rozdělena na dvě oblasti \( \displaystyle \Omega _{1}\) a \( \displaystyle \Omega _{2}\) , které mají společné nejvýše hraniční body. Platí
| \[ \int\int _{\Omega }f(x,y)\, \mathrm{d}x\, \mathrm{d}y =\int\int _{\Omega _{1}}f(x,y)\, \mathrm{d}x\, \mathrm{d}y +\int\int _{\Omega _{2}}f(x,y)\, \mathrm{d}x\, \mathrm{d}y \] |
3.3 Fyzikální aplikace dvojného integrálu
- Obsah množiny \( \displaystyle M\)
vypočteme jako
\[ \int\int _{M}\, \mathrm{d}x\, \mathrm{d}y. \] - Hmotnost množiny \( \displaystyle M\)
vypočteme jako
\[ m =\int\int _{M}\sigma (x,y)\, \mathrm{d}x\, \mathrm{d}y, \] kde \( \displaystyle \sigma (x,y)\) je plošná hustota (hmotnost vztažená na jednotku povrchu).
- Těžište hmotné množiny
\( \displaystyle M\) je
v bodě \( \displaystyle [x_{T},y_{T}]\) ,
kde
\[ \begin{align*}
x_{T} & = \frac{1}
{m}\int\int _{M}x\sigma (x,y)\, \mathrm{d}x\, \mathrm{d}y, & &
\\y_{T} & = \frac{1}
{m}\int\int _{M}y\sigma (x,y)\, \mathrm{d}x\, \mathrm{d}y & &
\\\end{align*}\]
a \( \displaystyle m\) je hmotnost množiny.
- Moment setrvačnosti hmotné množiny
\( \displaystyle M\)
vzhledem k ose je
\[ J =\int\int _{M}\rho ^{2}(x,y)\sigma (x,y)\, \mathrm{d}x\, \mathrm{d}y, \] kde \( \displaystyle \rho (x,y)\) je vzdálenost bodu \( \displaystyle (x,y)\) od osy otáčení. Například pro osu \( \displaystyle x\) je \( \displaystyle \rho (x,y) = y\) a pro osu \( \displaystyle y\) je \( \displaystyle \rho (x,y) = x\) . Pro osu procházející kolmo počátkem je \( \displaystyle \rho (x,y) = \sqrt{x^{2 } + y^{2}}\) .2
V dimenzování nábytku se setkáte s veličinami kvadratický moment průřezu (což je moment setrvačnosti pro \( \displaystyle \sigma (x,y) = 1\) ) a modul průřezu, která úzce souvisí s kvadratickým momentem a polohou těžiště. V případě hledání těžiště průřezu také klademe \( \displaystyle \sigma (x,y) = 1\) a hmotnost se tedy redukuje na obsah. Vzorce pro obsah (\( \displaystyle S\) ), \( \displaystyle x\) -ovou souřadnici těžiště (\( \displaystyle x_{T}\) ), \( \displaystyle y\) -ovou souřadnici těžiště (\( \displaystyle y_{T}\) ), kvadratický moment vzhledem k ose \( \displaystyle x\) (\( \displaystyle I_{x}\) ) a kvadratický moment vzhledem k ose \( \displaystyle y\) (\( \displaystyle I_{y}\) ) tedy jsou
\[ \eqalignno{ S & =\int\int _{M}\, \mathrm{d}x\, \mathrm{d}y & & & & \cr x_{T} & = \frac{1} {S}\int\int _{M}x\, \mathrm{d}x\, \mathrm{d}y, &\qquad I_{x} & =\int\int _{M}y^{2}\, \mathrm{d}x\, \mathrm{d}y & & & & \cr y_{T} & = \frac{1} {S}\int\int _{M}y\, \mathrm{d}x\, \mathrm{d}y, &I_{y} & =\int\int _{M}x^{2}\, \mathrm{d}x\, \mathrm{d}y & & & & \cr & & & & }\]
