Křivkový integrál druhého druhu

Pokud působíme na těleso silou \(F\) a přemísťujeme toto těleso ve směru působící síly po dráze délky \(s\), konáme práci \(W=Fs\). Pokud přemísťování neprobíhá ve směru působící síly a má-li síla směr \(\vec F\) a posunutí \(\vec s\), je práce rovna skalárnímu součinu \(\vec F\cdot\vec s\).

Předpokládejme, že na těleso působí (obecně nekonstantní) síla \(\vec F\) a těleso se pohybuje podél křivky \(C\) určené polohovým vektorem \(\vec r(t)\). Pro výpočet práce můžeme použít trik obvyklý v integrálním počtu. Rozdělíme dráhu na malé kousíčky a v rámci těchto kousíčků považujeme \(\vec F\) i \(\Delta \vec r\) za konstantu. Potom můžeme odhadnout příspěvek každého kousíčku k celkové práci klasickým způsobem pomocí skalárního součinu a nakonec všechny příspěvky sečíst. Tato aproximace bude tím přesnější, čím jemnější dělení použijeme.

V limitě dostáváme veličinu, která se nazývá křivkový integrál druhého druhu funkce \(\vec F\) po křivce \(C\). Tento integrál zapisujeme \[ \int_C\vec F\;\mathrm{d}\vec r .\] Je-li \[ \vec F(x,y)=P(x,y)\vec i+Q(x,y)\vec\jmath, \] zapisujeme někdy křivkový integrál ve složkách \[ \int_C P(x,y)\mathrm{d} x+Q(x,y)\mathrm{d} y. \]

Protože při pohybu tělesa po křivce jedním směrem se práce koná a při pohybu opačným směrem spotřebovává, je nutné, aby křivka figurující v křivkovém integrálu druhého druhu byla orientovaná. Musíme tedy prohlásit jeden koncový bod za počáteční a druhý za koncový. Vždy budeme předpokládat, že křivka je orientovaná v souladu se svým parametrickým vyjádřením, tj. že počáteční bod křivky odpovídá hodnotě parametru \(t=\alpha\) a koncový bod odpovídá hodnotě parametru \(t=\beta\).

Převod na Riemannův integrál

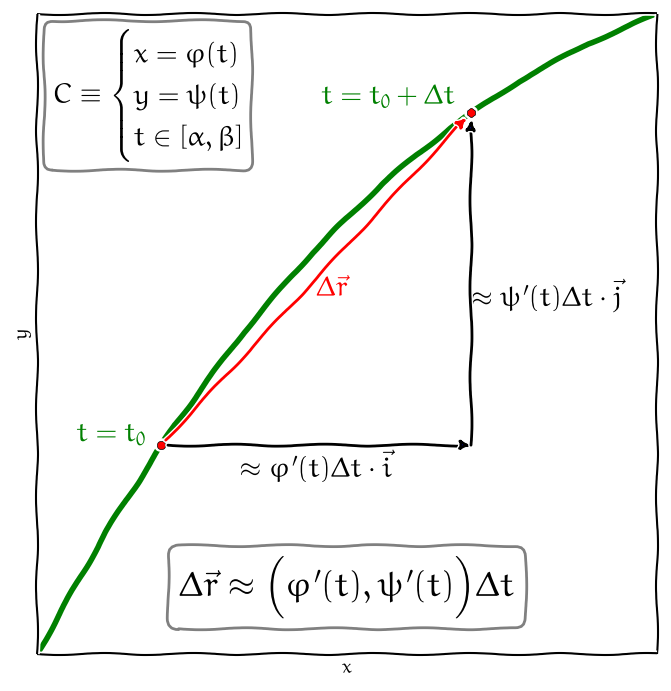
Známe-li parametrické rovnice \[\vec r(t) = \varphi(t)\vec\imath + \psi(t) \vec\jmath,\quad t\in[\alpha,\beta],\] křivky \(C\), je možno křivkový integrál druhého druhu funkce \[\vec F(x,y)=P(x,y)\vec\imath + Q(x,y)\vec\jmath\] po křivce \(C\) zapsat následovně \[ \begin{aligned} \int_C\vec F\;\mathrm{d}\vec r&= \int_\alpha^\beta\Bigl[ P(\varphi(t),\psi(t))\varphi'(t)\\ &\qquad +Q(\varphi(t),\psi(t))\psi'(t)\Bigr]\;\mathrm{d}t. \end{aligned} \]

Vlastnosti křivkového integrálu druhého druhu

Věta (souvislost křivkového integrálu a orientace křivky).

Změnou orientace křivky křivkový integrál druhého druhu mění znaménko.

Věta (nezávislost na zvolené parametrizaci).

Křivkový integrál druhého druhu nezávisí na konkrétní parametrizaci křivky \(C\). Pro různé parametrizace stejné křivky má integrál stejnou hodnotu.

Následující vlastnosti jsou stejné jako u křivkového integrálu prvního druhu.

Věta (linearita a aditivita vzhledem k integračnímu oboru).

Křivkový integrál druhého druhu je lineární vzhledem k funkci a aditivní vzhledem k oboru integrace. Přesněji, pro funkce \(\vec F\) a \(\vec G\) a konstantu \(k\) platí následující. \[ \begin{aligned} \int_C \vec F+\vec G\;\mathrm{d}\vec {r} & = \int_C \vec F\;\mathrm{d}\vec {r} + \int_C \vec {G}\;\mathrm{d}\vec{r} \\ \int_C k\vec {F}\;\mathrm{d}\vec{r} & = k\int_C \vec{F}\;\mathrm{d}\vec{r}\\ \end{aligned} \] Je-li křivka \(C\) rozdělena na dvě disjunktní (až na koncové body) křivky \(C_1\) a \(C_2\), platí \[ \int_{C} \vec F\;\mathrm{d}\vec{r} = \int_{C_1} \vec F\;\mathrm{d}\vec{r} + \int_{C_2} \vec F\;\mathrm{d}\vec{r} . \]

Aplikace křivkového integrálu druhého druhu

• Integrál \[ \int_C\vec F\;\mathrm{d}\vec r \] vyjadřuje práci kterou vykoná síla \(\vec F\) při přemístění tělesa podél orientované křivky \(C\).
• Je-li křivka \(C\) uzavřená, píšeme \[ \oint_C\vec F\;\mathrm{d}\vec r. \] Fyzikálně se jedná o práci kterou vykoná síla \(\vec F\) při přemístění tělesa po uzavřené orientované křivce. Tato práce se též nazývá cirkulace vektorového pole po orientované křivce \(C\). Pokud je možno v poli zavést potenciální energii a pokud tedy práce závisí jenom na počáteční a koncové poloze, musí tato práce být nulová. To je důsledkem věty kterou si uvedeme později.
• Při odvození křivkového integrálu druhého druhu jako vykonané práce hraje roli vlastně jenom ta složka silového pole, která při posunu ve směru křivky koná práci. Uvažujeme tedy jenom složku tečnou ke křivce. Pokud použijeme naopak pouze normálovou komponentu, dostaneme veličinu vyjadřující tok vektorového pole orientovanou křivkou \(C\). Výsledný vzorec pro tok vektorového pole \(\vec F(x,y)=P(x,y)\vec i+Q(x,y)\vec\jmath\) křivkou \(C\) je \[ \int_{C}-Q(x,y)\mathrm{d}x+P(x,y)\mathrm{d}y. \]
• Je-li množina \(\Omega\) “dostatečně pěkná” (např. souvislá, bez děr, s hladkou hranicí \(\partial \Omega\), která se nikde neprotíná, detaily uvedeme později u Greenovy věty), potom každý z integrálů \[\oint_{\partial\Omega}x\mathrm{d}y\qquad\text{a}\qquad\oint_{\partial\Omega}y\mathrm{d}x\] udává (až na případné znaménko) obsah množiny \(\Omega\). Na tomto principu fungují planimetry.

Online výpočet křivkového integrálu

• Křivkový integrál druhého druhu, numerický výpočet, Python.

• Vektorové pole \(\vec F\) se nazývá potenciálové, pokud existuje skalární funkce \(\varphi\) s vlastností \(\nabla \varphi=\vec F\). Funkce \(\varphi\) se nazývá kmenová funkce vektorového pole.
• Křivka \(C\) se nazývá uzavřená, pokud její počáteční a koncový bod splývají.
• Pokud platí pro libovolné dvě regulární křivky \(C\) a \(C_1\), které leží v \(\Omega\) a mají stejné počáteční body a stejné koncové body, platí \[ \int_C \vec F\mathrm{d}\vec r=\int_{C_1} \vec F\mathrm{d}\vec r, \] říkáme, že integrál v \(\Omega\) nezávisí na integrační cestě. Vektorové pole ve kterém křivkový integrál nezávisí na integrační cestě se nazývá konzervativní pole.

Věta o nezávislosti integrálu na integrační cestě

Podle této věty je tedy vektorové pole v prostoru konzervativní právě tehdy, když je jeho rotace nulová a to je právě tehdy, když pro toto pole existuje kmenová funkce a je tedy možno zavést potenciál (záporně vzatá kmenová funkce).

Věta (o nezávislosti integrálu na integrační cestě).

Uvažujme vektorovou funkci \(\vec F\), křivku \(C\) a oblast \(\Omega\) v \(\mathbb{R}^3\). Následující výroky jsou ekvivalentní za předpokladu hladkosti funkcí, regulárnosti křivek a jednoduše souvislé oblasti \(\Omega\).

1. Integrál \(\int_C \vec F\mathrm{d}\vec r\) nezávisí v \(\Omega\) na integrační cestě.
2. Křivkový integrál \(\oint_C \vec F\mathrm{d}\vec r\) po libovolné uzavřené křivce \(C\) v \(\Omega\) je roven nule.
3. Rotace \(\nabla\times \vec F\) vektorového pole \(\vec F\) je v \(\Omega\) rovna nulovému vektoru.
4. Existuje funkce \(\varphi\) s vlastností \(\nabla\varphi=\vec F\) na \(\Omega\).

Pokud jsou předchozí podmínky splněny (platnost jedné z nich vynutí platnost i všech ostatních), je možno křivkový integrál vypočítat podle vzorce \[ \int_C \vec F\mathrm{d}\vec r=\varphi(B)-\varphi(A), \] kde \(A\) a \(B\) jsou počáteční a koncový bod křivky \(C\) a \(\varphi\) je kmenová funkce vektorového pole \(\vec F\).

Tato věta je použitelná na mnoho způsobů.

• Věta přímo udává efektivní kritérium, kdy křivkový integrál nezávisí na integrační cestě. Rotace vektorového pole musí být nulová. Pokud máme vektorové pole zadané analytickým předpisem jednotlivých komponent, je toto nejsnazší kriterium na ověření.
• Věta přímo udává, jak ze znalosti kmenové funkce snadno určit hodnotu křivkového integrálu. Stačí vypočítat změnu kmenové funkce (změnu skalárního potenciálu) mezi počátečním a koncovým bodem křivky.
• Věta také udává, jak vypočítat skalární potenciál pomocí křivkového integrálu. Ač se ve sbírkách příkladů studenti setkávají s výpočtem křivkového integrálu pomocí skalárního potenciálu, je toto typické využití jenom v případech s analyticky snadným řešením. V případě numerických výpočtů s naměřenými daty je hledání skalárního potenciálu v podstatě nemožné provést klasickou cestou. Pomocí křivkového integrálu to je naopak snadné. Stačí si vybrat výchozí bod a počítat křivkové integrály po libovolných křivkách (zpravidla úsečky) do bodů, kde chceme znát skalární potenciál. Tomuto je věnován Jupyter zápisník ilustrující uvedenou větu.

Plošný integrál druhého druhu

Výše uvedené myšlenky je možno zobecnit na případ toku vektorového pole dvourozměrnou plochou. Například tok o hustotě \(F\) kolmo na plochu o průřezu o obsahu \(S\) je dán vzorcem \[ Q = FS.\] Pokud není tok kolmý, musíme uvažovat jenom komponentu ve směru normály k ploše, tj. \[ Q = \vec F\vec S, \] kde vektor \(\vec S\) je kolmý k ploše a má velikost rovnu obsahu. Pokud nejsou vektorové pole nebo normála k ploše konstantní pro celou plochu, vypočítáme příspěvek na každé komponentě samostatně a výsledky sečteme, tj. \[Q=\sum_{i} \vec F_i \vec S_i.\] Pokud se veličiny nemění po skocích, ale spojitě, můžeme tento proces udělat s nekonečně jemným dělením. Výsledný matematický objekt se nazývá plošný integrál druhého druhu a značíme jej \[\iint_{\Omega} \vec F\vec{\mathrm dS}.\] Vyjadřuje celkový tok vektorového pole \(\vec F\) plochou \(\Omega\).