1 Metody s konstatním krokem

Řešíme počáteční úlohu pro diferenciální rovnici prvního řádu rozřešenou vzhledem k derivaci:¹ \( \displaystyle \left \{\begin{aligned}y' & = f(x,y)& \\y(x_{0})& = y_{0} \\ \end{aligned}\right .\)

Řešení aproximujeme po částech lomenou čarou (viz obrázky 5.2 a 5.3), vodorovná vzdálenost mezi jednotlivými uzly se nazývá krok, označujeme jej \( \displaystyle h\), má-li další část lomené čáry směrnici \( \displaystyle k\), dostaneme další bod pomocí vztahů \( \displaystyle \left \{\begin{aligned}x_{i+1}& = x_{i} + h & \\y_{i+1}& = y_{i} + kh \\ \end{aligned}\right .\)

Uvedeme si na ukázku metody s pevným krokem, kdy neměníme krok, ale pouze směr lineární funkce, která aproximuje integrální křivku. Podle toho, jak v jednotlivých krocích volíme směrnici aproximační funkce, rozlišujeme několik metod.

Eulerova metoda

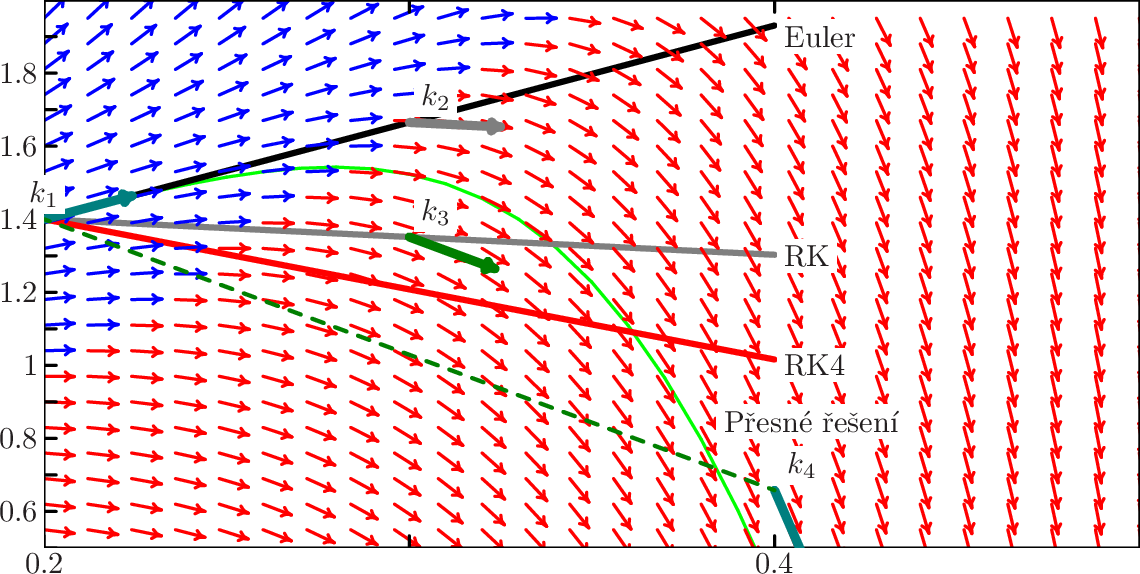
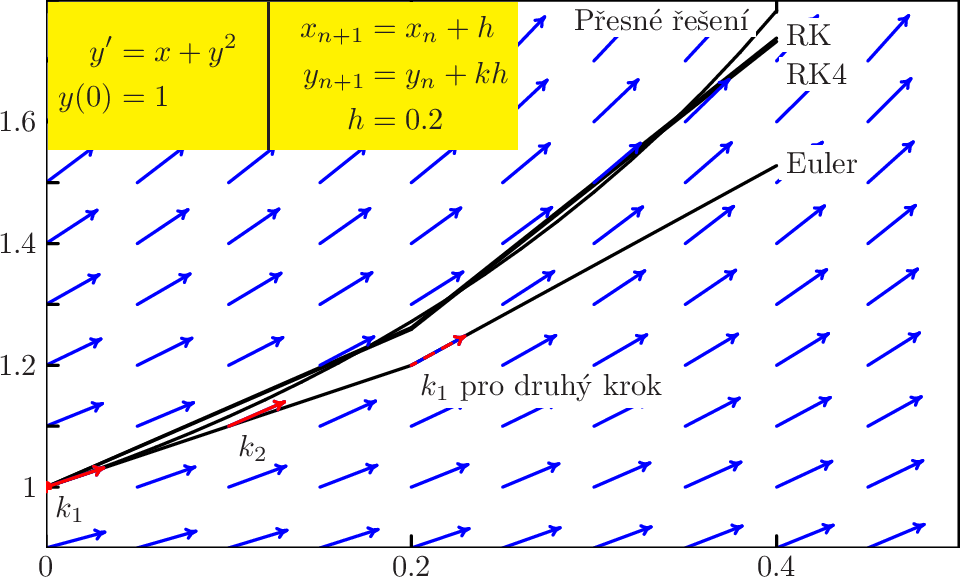
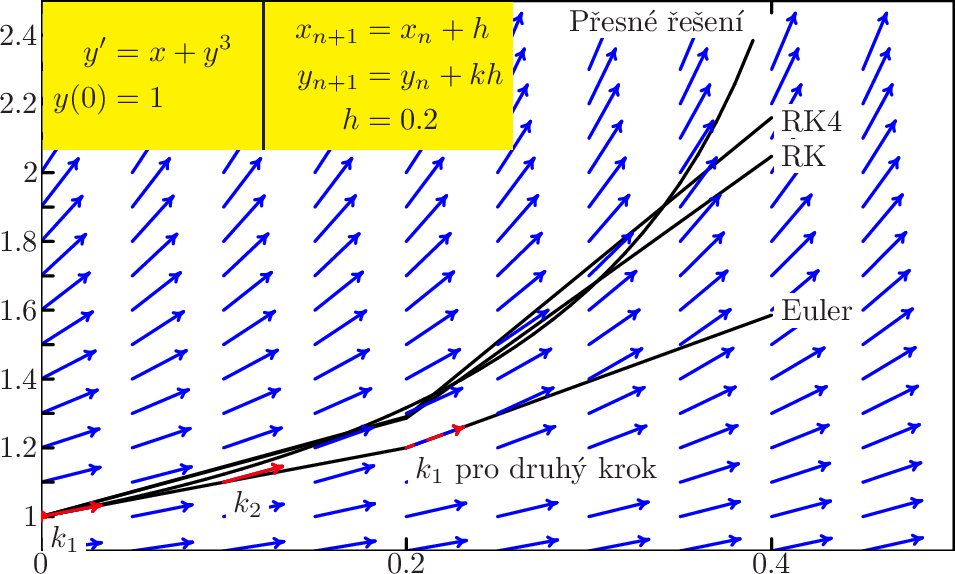
Jako směrnici tečny použijeme hodnotu směrového pole v bodě, ze kterého vycházíme: \( \displaystyle k = k_{1} := f(x_{i},y_{i})\)

RK

(metoda Runge-Kutta druhého řádu) Jako směrnici tečny použijeme hodnotu směrového pole v bodě, do kterého bychom se dostali po provedení půlky kroku Eulerovou metodou. Podíváme se tedy, kam bychom se dostali Eulerovou metodou, podíváme se jak po cestě vypadá směrové pole a podle toho zvolíme výchozí směr: \( \displaystyle k = k_{2} := f\left (x_{i} +{ h \over 2} ,y_{i} + k_{1}{ h \over 2} \right )\)

RK4

(metoda Runge-Kutta čtvrtého řádu) Zde se jedná o poněkud rafinovanější variantu předchozího. Hlavní myšlenka spočívá v tom že podobně jako u metody druhého řádu uděláme fiktivně půl kroku směrem \( \displaystyle k_{1}\) podle Eulerovy metody a ze směrového pole v bodě do kterého se dostaneme získáme směr \( \displaystyle k_{2}\). Poté podobně provedeme opět fiktivně půl kroku směrem \( \displaystyle k_{2}\) a ze směrového pole v bodě, do kterého se dostaneme, získáme směr \( \displaystyle k_{3}\). Konečně, směrem \( \displaystyle k_{3}\) provedeme fiktivně celý krok a získáme směr \( \displaystyle k_{4}\). Ze všech těchto směrů vypočítáme vážený průměr ve kterém jsou \( \displaystyle k_{2}\) a \( \displaystyle k_{3}\) zastoupeny dvojnásobnou vahou oproti \( \displaystyle k_{1}\) a \( \displaystyle k_{4}\) a získáme směr pro provedení dalšího kroku metody. K předešlým vzorcům tedy přidáváme: \( \displaystyle k ={ 1 \over 6} (k_{1} + 2k_{2} + 2k_{3} + k_{4})\),
kde \( \displaystyle k_{3} := f\left (x_{i} +{ h \over 2} ,y_{i} + k_{2}{ h \over 2} \right )\) a \( \displaystyle k_{4} := f(x_{i} + h,y_{i} + k_{3}h)\)

• Stejně se postupuje i pro systém libovolného počtu lineárních rovnic prvního řádu. Například pro autonomní systém \( \displaystyle \left \{\begin{aligned}x'& = f(x,y)& \\y'& = g(x,y) \\ \end{aligned}\right .\), počáteční podmínku \( \displaystyle \left \{\begin{aligned}x(0)& = x_{0},& \\y(0)& = y_{0} \\ \end{aligned}\right .\) a Eulerovu metodu s krokem \( \displaystyle h\) dostáváme \( \displaystyle \left \{\begin{aligned}t_{i+1} & = t_{i} + h & \\x_{i+1}& = x_{i} + hf(x_{i},y_{i}) \\y_{i+1}& = y_{i} + hg(x_{i},y_{i}) \\ \end{aligned}\right ..\)
• Diferenciální rovnici druhého řádu \( \displaystyle y'' + p(x)y' + q(x)y = f(x)\) můžeme substitucí \( \displaystyle y_{1} = y\), \( \displaystyle y_{2} = y'\) přepsat na systém \( \displaystyle \left \{\begin{aligned}y_{1}'& = y_{2} & \\y_{2}'& = f(x) - p(x)y_{2} - q(x)y_{1} \\ \end{aligned}\right .\)