Křivkový integrál

Křivkový integrál je rozšíření Riemannova integrálu na případ, kdy množinou, přes kterou integrujeme, je místo úsečky obecnější křivka. Pro jednoduchost budeme uvažovat dvourozměrnou křivku v rovině \(x\), \(y\).

Rozeznáváme dva druhy křivkových integrálů. První z nich používáme při práci se skalárními veličinami. Příkladem je kvadratický moment. (Objekty s velkým kvadratickým momentem jsou při rotačních pohybech obdobou objektů velké hmotnosti při posuvných pohybech.) Druhý z křivkových integrálů používáme při práci ve vektorovém poli. Příkladem je výpočet práce vykonané po křivce nebo tok křivkou.

Parametrické rovnice křivky

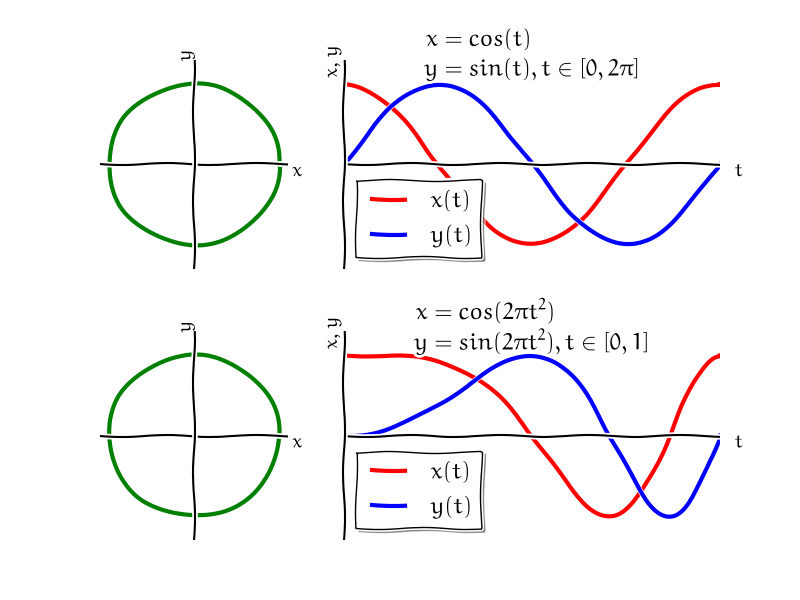
Nejprve představíme matematický aparát pro popis křivek. Rovinné křivky nejčastěji popisujeme vektorovou funkcí jedné proměnné \(\vec r\colon \mathbb{R}\to \mathbb{R}^2\). Zpravidla s touto vektorovou funkcí pracujeme v komponentách, kdy každá její komponenta je dána skalární funkcí. Vektorově píšeme \[\vec r(t)=[\varphi(t),\psi(t)]=\varphi(t) \vec\imath + \psi(t)\vec\jmath,\quad t\in [\alpha,\beta]\] a tato vektorová funkce se nazývá parametrizace křivky \(C\). Často píšeme parametrické rovnice pro jednotlivé souřadnice ve tvaru \[C=\begin{cases} x=\varphi(t)\\y=\psi(t), \quad t\in[\alpha,\beta].\end{cases}\]

• Graf křivky dostaneme tak, že pro každé \(t\) z intervalu \([\alpha, \beta]\) kreslíme ve 2D bod \([\varphi(t), \psi(t)]\).
• Pro danou křivku \(C\) v rovině \(xy\), nejsou její parametrické rovnice dány jednoznačně. Nakreslit online.

Křivkový integrál prvního druhu

Pokud uvažujeme rovný drát o lineární hustotě \(f\) a délce \(s\), je hmotnost drátu rovna součinu \[m=fs.\] Pokud by drát nebyl homogenní, je nutné v tomto vzorci místo součinu použít Riemannův integrál \[m=\int _a^b f\,\mathrm ds.\] Budeme ve zobecňování pokračovat. Uvažujme drát, který není ani homogenní, ani rovný. Nechť leží podél rovinné křivky \(C\) a nechť je jeho lineární hustota (specifická hmotnost) v bodě \((x,y)\) dána funkcí \(f(x,y)\). Zde již Riemannův integrál nepomůže. Celkovou hmotnost můžeme odhadnout následovně.

• Myšlenkově rozdělíme drát na malé kousíčky a v každém z nich odhadneme lineární hustotu konstantou. Můžeme například použít minimální hodnotu hustoty v tomto kousíčku pro dolní odhad hmotnosti.
• Vynásobením délky každého kousíčku a lineární hustotou obdržíme jeho hmotnost a sečtením přes všechny kousky dostaneme odhad pro hmotnost drátu. Tento odhad bude tím přesnější, čím jemnější dělení použijeme.
• Zjemňováním dělení se tyto odhady zpřesňují.

V limitním procesu můžeme nechat délku kousíčků konvergovat k nule. Poté dostáváme objekt, který se nazývá křivkový integrál prvního druhu, označuje \[ \int_C f\;\mathrm{d} s \] a fyzikálně vyjadřuje hmotnost drátu z výše uvažované úlohy. Pokud počáteční a koncový bod křivky \(C\) splývají, píšeme též \[ \oint_C f\;\mathrm{d} s \] a integrál nazýváme integrálem po uzavřené křivce.

Převod na Riemannův integrál (rovinná křivka)

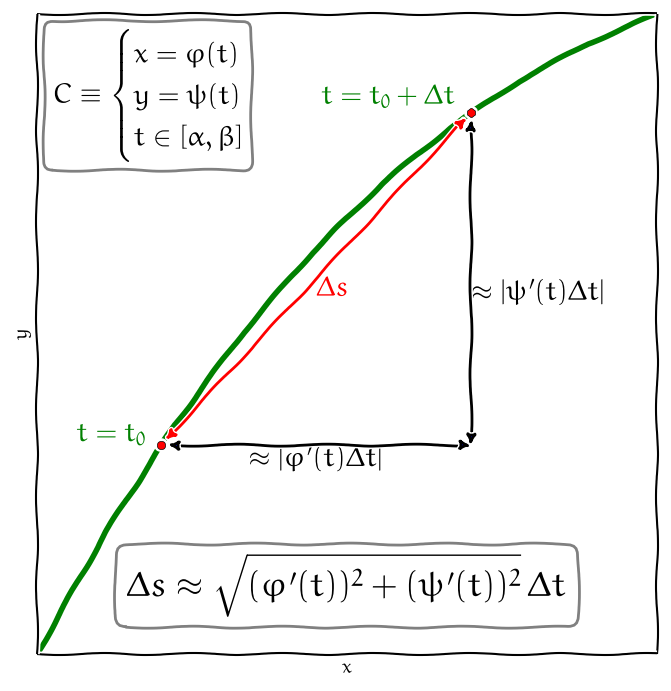
Mějme parametrické rovnice křivky \(C\) ve vektorovém tvaru \[\vec r(t)=\varphi(t) \vec\imath + \psi(t)\vec\jmath,\] kde \(t\in[\alpha,\beta]\). Derivováním křivky dostaneme \[\frac{\mathrm{d} \vec r(t)}{\mathrm{d}t}=\varphi'(t) \vec\imath + \psi'(t)\vec\jmath.\] Výpočtem délky vektoru (a formálním vynásobením výrazem \(\mathrm{d}t\)) dále \[\mathrm{d}s=|\mathrm{d}\vec r(t)|=\sqrt{(\varphi'(t))^2 + (\psi'(t))^2}\mathrm{d}t.\] Tím se křivkový integrál prvního druhu funkce \(f(x,y)\) po křivce \(C\) transformuje na Riemannův integrál \[ \int_C f\;\mathrm{d} s=\int_\alpha^\beta f(\varphi(t),\psi(t))\sqrt{\varphi^{\prime 2}(t)+\psi^{\prime 2}(t)}\;\mathrm{d} t. \]

Převod na Riemannův integrál (prostorová křivka)

S křivkovým integrálu po křivce
\[ C:\quad \varphi(t)\vec\imath + \psi(t)\vec\jmath + \xi(t) \vec k, \quad t\in[\alpha,\beta] \] ve trojrozměrném prostoru pracujeme podobně. Délkový element je \[ \mathrm{d}s=\sqrt{(\varphi^{\prime}(t))^2+(\psi^{\prime }(t))^2+(\xi^{\prime }(t))^2}\mathrm{dt} \] a integrál má tvar \[ \int_C f\;\mathrm{d} s=\int_\alpha^\beta f(\varphi(t),\psi(t),\xi(t))\sqrt{(\varphi^{\prime}(t))^2+(\psi^{\prime }(t))^2+(\xi^{\prime }(t))^2}\;\mathrm{d} t. \]

Aplikace křivkového integrálu prvního druhu

Funkce \(f(x,y)\)	Integrál \(\int_C f\;\mathrm{d}s\)
\(1\)	délka křivky \(C\)
lineární hustota \(\tau(x,y)\)	hmotnost \(m_C\) křivky \(C\)
\(\frac {1}{m_C}[x\tau(x,y),y\tau(xy)]\)	souřadnice těžiště křivky \(C\)
\(x^2\tau(x,y)\)	moment setrvačnosti křivky \(C\) vzhledem k ose \(y\)
\(y^2\tau(x,y)\)	moment setrvačnosti křivky \(C\) vzhledem k ose \(x\)
\(\rho^2(x,y)\tau(x,y)\)	moment setrvačnosti křivky \(C\) vzhledem k obecné ose, kde \(\rho(x,y)\) je vzdálenost bodu \([x,y]\) od osy otáčení.

Vlastnosti křivkového integrálu prvního druhu

Věta (nezávislost na zvolené parametrizaci).

Křivkový integrál prvního druhu nezávisí na konkrétní parametrizaci křivky \(C\). Pro různé parametrizace stejné křivky má integrál stejnou hodnotu.

Věta (linearita).

Pro funkce \(f\) a \(g\) a konstantu \(k\) platí následující. \[ \begin{aligned} \int_C f+g\;\mathrm{d}s & = \int_C f\;\mathrm{d}s + \int_C g\;\mathrm{d}s \\ \int_C kf\;\mathrm{d}s & = k\int_C f\;\mathrm{d}s\\ \end{aligned} \]

Věta (aditivita vzhledem k integračnímu oboru).

Nechť je křivka \(C\) rozdělena na dvě křivky \(C_1\) a \(C_2\), které jsou disjunktní (až na koncové body). Potom platí \[ \int_{C} f\;\mathrm{d}s = \int_{C_1} f\;\mathrm{d}s + \int_{C_2} f\;\mathrm{d}s . \]

Proč trubky praskají podélně?

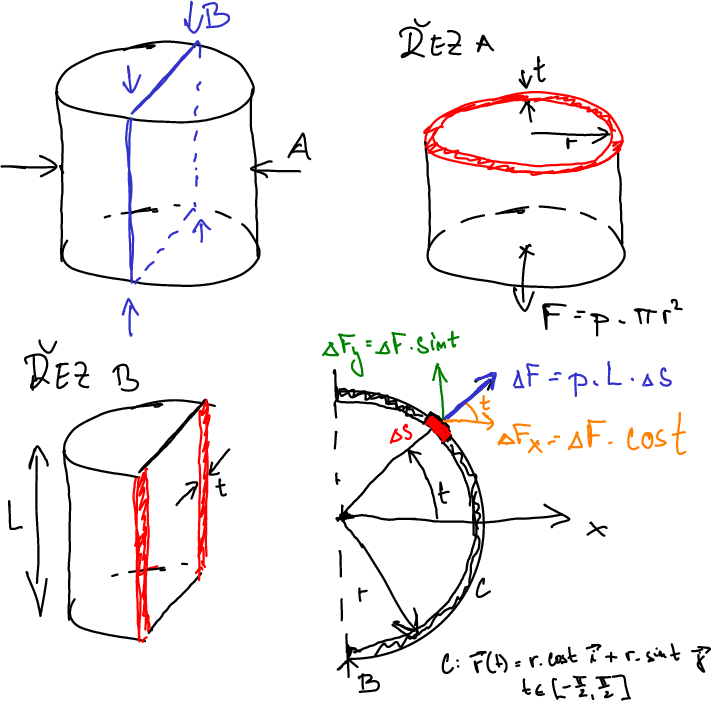
Ukážeme si aplikaci křivkového integrálu prvního druhu k tomu, abychom sečetli komponenty síly, snažící se roztrhnout natlakovanou válcovou nádobu. Tlaková síla je ve všech částech nádoby stejně velká. Protože je však kolmá ke stěně nádoby, mění se směr síly a tím i průměty síly do směru, ve kterém počítáme namáhání. Zjednodušíme si situaci tím, že budeme uvažovat průmět stěny do roviny podstavy, kdy se stěna redukuje na křivku.

Vypočteme síly, které se snaží roztrhnout válec napříč (viz řez A v obrázku) a podélně (viz řez B v obrázku). Tato dvě namáhání porovnáme. Ještě existuje namáhání radiálně od osy. Ale v tomto případě se tlaková síla rozkládá na celou plochu pláště válce a v tomto směru je namáhání minimální. Proto toto namáhání nemusíme uvažovat.

Uvažujme natlakovanou válcovou nádobu s tlakem \(p\), výškou \(L\), poloměrem podstavy \(r\) a stěnou o tloušťce \(t\).

Výpočet namáhání v řezu A je snadný. Obsah řezu (vyšrafováno červeně) je \(2\pi r t\). Na dno a víko působí síla \(F=p\pi r^2\) a v řezu A je tahové napětí \[\sigma_{p} = \frac FS=\frac {p\pi r^2}{2\pi rt}=\frac {pr}{2t}.\]

Nyní vypočteme namáhání, které se snaží roztrhnout válec podélně. K tomu musíme vypočítat sílu, která působí po obvodě válce, tj. která se snaží válec roztrhnout v řezu B. Obsah řezu (červeně vyznačeno) je \(2Lt\). Nejtěžší bude najít celkovou sílu, která od sebe oddaluje dvě poloviny pláště. To je místo, kde zapojíme integrál.

Budeme se na úlohu dívat shora ze směru, kterým míří osa válce. Tím můžeme snížit dimenzionalitu úlohy. Plášť válce v tomto pohledu vidíme jako kružnici a polovinu pláště jako půlkružnici. Tato půlkružnice má rovnici \(\vec r(t)=r\cos(t)\vec\imath+r\sin (t)\vec\jmath\), kde \(r\) je poloměr válce a \(t\in\left[-\frac \pi 2,\frac \pi 2\right]\) je úhel mezi spojnicí elementu v bodě \((x,y)\) a mezi kladnou částí osy \(x\). Kousek pláště válce odpovídající v průmětu úseku křivky délky \(\Delta s\) má obsah \(L\Delta s\). Tlaková síla na tento kousek je součin tlaku a obsahu, tj. \[\Delta F=pS=p L\Delta s.\] Směr je kolmý k plášti válce a s vodorovnou osou proto síla svírá úhel \(t\). Průmět této síly do vodorovného směru je \[\Delta F_x=pL\Delta s \cos t\] a tyto příspěvky musíme sečíst křivkovým integrálem přes celou křivku. Platí \(\mathrm ds=r\mathrm dt\). Celková síla, která se snaží nádobu roztrhnout podélně je \[F_x=\int_C pL \cos t \,\mathrm d s = \int_{-\frac \pi 2}^{\frac \pi 2} pLr \cos t \,\mathrm d t =prL [\sin t]_{-\frac \pi 2}^{\frac \pi 2}=prL \left[\sin\frac \pi 2 -\sin\left(-\frac \pi2 \right)\right]=2p rL.\] Povrch, na který tato síla působí, odpovídá dvěma podélným hranám (červeně na řezu B), tj. má obsah \(2Lt\) a napětí je tedy \[\sigma_{h}=\frac{2pLr}{2Lt}=\frac{pr}t=2\sigma_p.\] Vidíme, že toto napětí je dvojnásobkem napětí v podélné ose.

Ještě je vhodné ověřit, že svislý průmět, tj . \[\Delta F_y=pL\Delta s \sin t\] k namáhání nepřispívá, protože \[F_y=\int_{C} pL \sin t \,\mathrm d s =0.\] To však je možné očekávat i ze symetrie.

Pokud se chcete dozvědět o problematice více, nebo si prohlédnout obrázky válcových nádrží, které selhaly vlivem vysokého nebo nízkého tlaku, zkuste Google a heslo “hoop stress”.

Dvojný integrál

Pro dvojný integrál použijeme podobnou myšlenkovou konstrukci jako u křivkového integrálu prvního druhu, pouze místo drátu s danou lineární hustotou budeme uvažovat rovinnou ohraničenou desku s danou plošnou hustotou.

• Pokud je hustota desky konstantní, je možno její hmotnost získat jednoduše jako součin plošné hustoty a obsahu.
• Pokud se hustota desky mění a v obecném bodě \((x,y)\) je dána funkcí \(f(x,y)\), můžeme myšlenkově rozdělit desku na malé kousky, v rámci každého malého kousku hustotu aproximovat konstantou, vypočítat hmotnost každého kousku jako součin hustoty a obsahu a všechny hmotnosti sečíst.
• Získaná veličina je aproximací celkové hmotnosti.

V limitním přechodu kdy rozměry všech kousků na něž je deska dělena jdou k nule dostáváme dvojný integrál \[ \iint_\Omega f(x,y)\mathrm{d}x \mathrm{d}y , \] kde \(\Omega\) je oblast v rovině \((x,y)\) definovaná uvažovanou deskou. V aplikacích je častý též zápis \[ \iint_\Omega f(x,y)\mathrm{d}A\] nebo \[ \iint_\Omega f(x,y)\mathrm{d}S.\]

Linearita a aditivita

Dvojný integrál je odvozen (tak jako všechny integrály) pro aditivní veličiny a proto se “dobře snáší” se sčítáním (ať už integrovaných funkcí, nebo integračních oborů) a s násobení integrované funkce konstantou. Přesněji, platí následující věty.

Věta (linearita dvojného integrálu).

Buď \(f_1\), \(f_2\) funkce integrovatelné v \(\Omega\) a \(c_1\), \(c_2\) libovolná reálná čísla. Platí \[ \iint_{\Omega} \bigl[c_1f_1(x,y)+c_2f_2(x,y)\bigr]\mathrm dx\mathrm dy = c_1\iint_{\Omega} f_1(x,y)\mathrm dx\mathrm dy+ c_2\iint_{\Omega} f_2(x,y)\mathrm dx\mathrm dy \]

Věta (aditivita vzhledem k oboru integrace).

Nechť je množina \(\Omega\) rozdělena na dvě oblasti \(\Omega_1\) a \(\Omega_2\), které mají společné nejvýše hraniční body. Platí \[ \iint_\Omega f(x,y)\mathrm dx\mathrm dy= \iint_{\Omega_1} f(x,y)\mathrm dx\mathrm dy+ \iint_{\Omega_2} f(x,y)\mathrm dx\mathrm dy. \]

Výpočet dvojného integrálu

Výpočet dvojného integrálu se provádí převodem, na integrály funkcí jedné proměnné.

Výpočet (oblast mezi funkcemi proměnné \(x\))

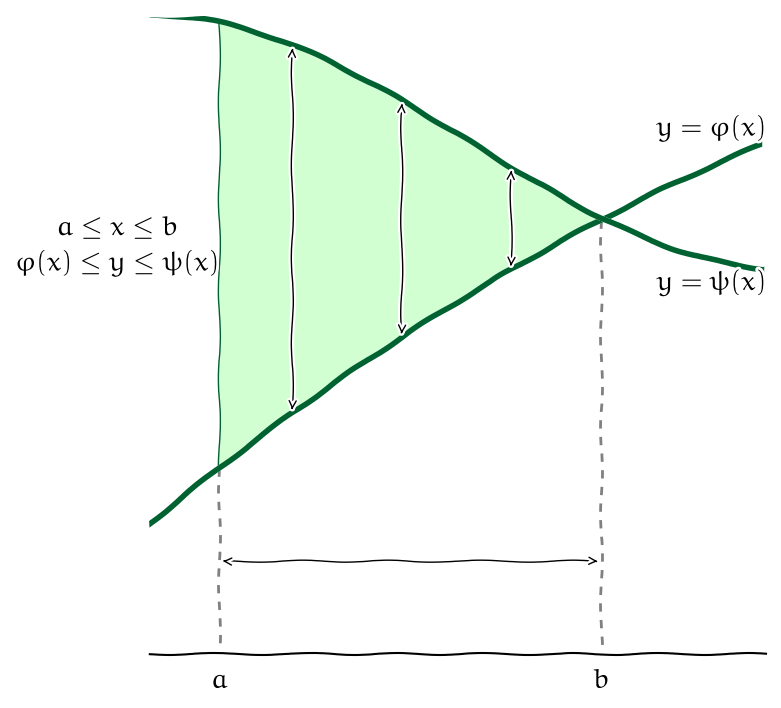
V závislosti na tom, jakými nerovnostmi množinu \(\Omega\) definujeme, můžeme pro výpočet dvojného integrálu použít následující věty. Tyto věty udávají, jak je možno dvojný integrál přepsat jako dvojnásobný integrál. Mají název Fubiniovy věty.

Věta (Fubiniova věta).

Nechť \(f\) je funkce spojitá v uzavřené oblasti \[ \Omega=\{(x,y)\in\mathbb{R}^2:{a\leq x\leq b}\text{ a } {\varphi (x)\leq y\leq \psi (x)}\}.\] Potom \[ \iint_{\Omega}f(x,y)\mathrm{d}x \mathrm{d}y ={\int_{a}^{b}} \Bigl[ \int_{\varphi (x)}^{\psi(x)} f(x,y){\mathrm{d}y }\Bigr]{\mathrm{d}x }. \]

Výpočet (oblast mezi funkcemi proměnné \(y\))

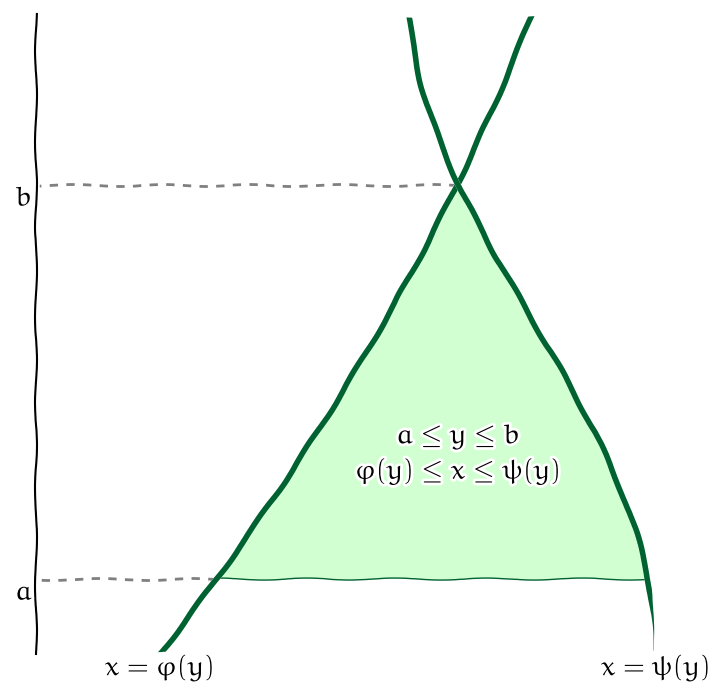
Věta (Fubiniova věta pro jiné pořadí integrace).

Nechť \(f\) je funkce spojitá v uzavřené oblasti \[ \Omega=\{(x,y)\in\mathbb{R}^2:{a\leq y\leq b}\text{ a } {\varphi (y)\leq x\leq \psi (y)}\}. \] Potom \[ \iint_{\Omega}f(x,y)\mathrm{d}x \mathrm{d}y ={\int_a^b}\Bigl[ {\int_{\varphi (y)}^{\psi(y)}} f(x,y){\mathrm{d}x }\Bigr]{\mathrm{d}y }. \]

Záměna pořadí integrace

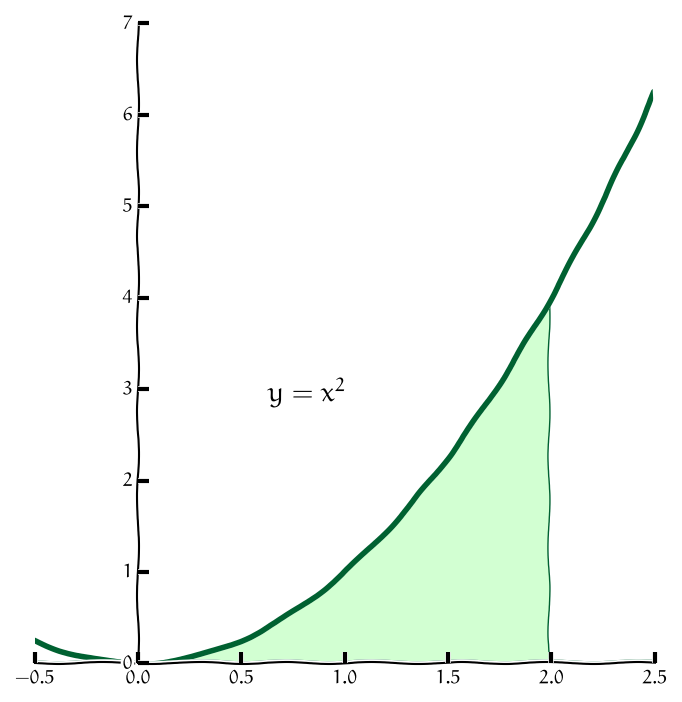
Často je možné oblast integrace zapsat pomocí obou možností uvedených na předchozích slidech. Například oblast na obrázku je možno zapsat buď jako \[\begin{gathered} 0\leq x \leq 2\\ 0\leq y\leq x^2 \end{gathered}\] nebo \[\begin{gathered} 0\leq y \leq 4\\ \sqrt{y}\leq x\leq 2. \end{gathered}\]

Pro integrál funkce \(f(x,y)\) přes takovou množinu tedy máme dvě alternativy. Buď \[\int_0^2 \int _0^{x^2} f(x,y)\;\mathrm{d}y\;\mathrm{d}x\] anebo \[\int_0^4 \int _{\sqrt y}^{2} f(x,y)\;\mathrm{d}x\;\mathrm{d}y.\]

Všimněte si, že nestačí prosté prohození integrálů. Je nutno přepočítávat meze a hraniční křivky je nutno vyjádřit jednou jako funkce proměnné \(x\) a jednou jako funkce proměnné \(y\). V důsledku tohoto dochází v průběhu výpočtu dvěma různými způsoby k tomu, že pracujeme se dvěma různými integrály. Výsledky jsou samozřejmě stejné, ale nemusí být dosažitelné srovnatelnou námahou. Jedna z cest může být snazší.

Výpočet (obdélníková oblast)

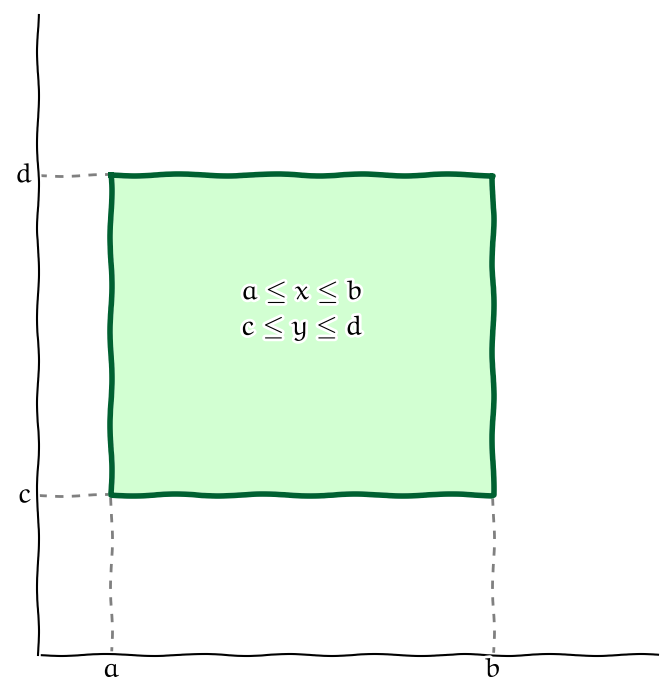
Výše uvedené problémy se stanovením a případným přepočítáváním mezí při záměně pořadí integrace se nevyskytují při integrování přes obdélníkovou oblast.

Věta (Fubiniova věta na obdélníku).

Nechť \(R=[a,b]\times[c,d]\) je uzavřený obdélník v \(\mathbb{R}^2\) a \(f\) funkce definovaná a spojitá na \(R\). Pak platí \[ \begin{aligned}\iint_R f(x,y)\mathrm{d}x \mathrm{d}y &= \int_a^b\Bigl[\int_c^d f(x,y)\mathrm{d}y \Bigr]\mathrm{d}x \\&= \int_c^d\Bigl[\int_a^b f(x,y)\mathrm{d}x \Bigr]\mathrm{d}y .\end{aligned} \]

Platí-li dokonce rovnost \(f(x,y)=g(x)h(y)\), pak \[ \iint_R f(x,y)\mathrm{d}x \mathrm{d}y = \int_a^b g(x) \mathrm{d}x \int_c^d h(y)\mathrm{d}y . \]

Aplikace dvojného integrálu

Matematické aplikace dvojného integrálu

• Obsah \(\mu(\Omega)\) množiny \(\Omega\) vypočteme jako integrál \[\mu(\Omega)=\iint_\Omega \mathrm{d}x \mathrm{d}y.\]
• Integrální střední hodnota funkce \(f(x,y)\) definované na množině \(\Omega\) je \[ \frac{\iint_\Omega f(x,y)\mathrm{d}x \mathrm{d}y }{\mu (\Omega)},\] kde \(\mu (\Omega)=\iint_\Omega\mathrm{d}x\mathrm{d}y\) je obsah množiny \(\Omega\).

Objem kopce nebo jezera pomocí vrstevnic

• Obsah množiny ohraničené vrstevnicí na mapě vynásobený rozestupem mezi vrstevnicemi je přibližně roven objemu vrstvy mezi dvěma vrstevnicemi.
• Pokud sečteme obsahy všech vrstevnic a vynásobíme rozestupem mezi těmito vrstevnicemi, dostaneme odhad pro objem kopce. Vlastně je to jako bychom kopec rozřezali na stejně tlusté plátky, naskládali je vedle sebe, sečetli obsahy postav takto vzniklých těles a vynásobili výškou.
• Podobně je možné odhadnout objem jezera.
• V tomto případě je dvojný integrál pouze koncept. Samozřejmě nemáme ambice vyjadřovat vrstevnice v analytickém tvaru a integrovat pomocí Fubiniovy věty. Ke slovu přijde spíše numerický výpočet integrálu.

Fyzikální aplikace dvojného integrálu

• Hmotnost množiny \(M\) je \[m=\iint_M \sigma(x,y)\mathrm{d}x \mathrm{d}y,\] kde \(\sigma(x,y)\) je plošná hustota (hmotnost vztažená na jednotku povrchu).
• Je-li plošná \(u\) hustota kinetické energie molekul (což je veličina úměrná termodynamické teplotě), je \(\iint_M u\,\mathrm dx\mathrm dy\) celková kinetická energie částic. Tato energie se může měnit tepelnou výměnou. Rychlost, s jakou se mění část vnitřní energie související s teplotou, je \[\frac{\mathrm d}{\mathrm d t}\left(\iint_M u\,\mathrm dx\mathrm dy\right)\] a odsud odvozujeme rovnici vedení tepla.
• Lineární momenty hmotné množiny \(M\) vzhledem k osám \(y\) a \(x\) jsou rovny \[\iint_M x\sigma(x,y)\mathrm{d}x \mathrm{d}y\] a \[\iint_M y\sigma(x,y)\mathrm{d}x \mathrm{d}y.\]
• Moment setrvačnosti hmotné množiny \(M\) vzhledem k ose je \[J=\iint_M \rho^2(x,y)\sigma(x,y)\mathrm{d}x \mathrm{d}y ,\] kde \(\rho(x,y)\) je vzdálenost bodu \((x,y)\) od osy otáčení. Například pro osu \(x\) je \(\rho(x,y)=y\) a pro osu \(y\) je \(\rho (x,y)=x\). Pro osu procházející kolmo počátkem je \(\rho(x,y)=\sqrt{x^2+y^2}\).

Technické aplikace dvojného integrálu

• Souřadnice těžiště množiny jsou podílem lineárních momentů a celkové hmotnosti množiny.
• Kvadratický moment průřezu (což je moment setrvačnosti pro \(\sigma(x,y)=1\), anglicky second moment of area) je veličina, která hraje podstatnou roli v mechanice (nábytek, stavby) při dimenzování (polic, nosných tyčí, nosníků).
• V technické praxi zpravidla neuvažujeme nekonstantní plošnou hustotu. Potom je možné je bez újmy na obecnosti nahradit jedničkou. Vzorce pro obsah, \(x\)-ovou souřadnici těžiště (\(x_0\)), \(y\)-ovou souřadnici těžiště (\(y_0\)), kvadratický moment vzhledem k ose \(x\) (\(I_x\)) a kvadratický moment vzhledem k ose \(y\) (\(I_y\)) (pro množinu \(M\) s plošnou hustotou \(1\)) jsou \[ \begin{alignedat}{2} % S&=\iint_M\mathrm{d}x \mathrm{d}y \\ x_0&=\frac 1S \iint_M x\mathrm{d}x \mathrm{d}y ,&\qquad I_x&= \iint_M y^2\mathrm{d}x \mathrm{d}y, \\ y_0&=\frac 1S \iint_M y\mathrm{d}x \mathrm{d}y , & I_y&= \iint_M x^2\mathrm{d}x \mathrm{d}y, \\ \end{alignedat} \] kde \(S=\mu (M)\) je obsah množiny \(M\). Poloha těžiště je tedy střední hodnotou funkcí \(x\) a \(y\).

Tuhost nosníků, stabilita stromů

Tuhost (odolnost vůči deformaci) pro nosník obdélníkového průřezu o výšce \(b\) a šířce \(a\) je dána kvadratickým momentem obdélníkového průřezu vzhledem k vodorovné ose procházející těžištěm. \[\begin{aligned}I_x&= \iint_{\left[-\frac a2,\frac a2\right]\times \left[-\frac b2,\frac b2\right]} y^2\,\mathrm dx\mathrm dy\\ &= \int_{-\frac a2}^{\frac a2} \,\mathrm dx\int_{-\frac b2}^{\frac b2} y^2 \,\mathrm dy= a\left[\frac 13 y^3\right]_{-\frac b2}^{\frac b2} =\frac 1{12}ab^3 \end{aligned} \] Odsud máme okamžitě několik pozorování

• Pokud šířka vzroste dvakrát, tuhost vzroste také dvakrát. Pokud ale dvakrát vzroste výška, tuhost vzroste dokonce osmkrát. Pro nosník s poměrem stran 1:2 je poměr tuhostí při poloze naplacato a nastojato roven 1:4.
• Pro nosník čtvercového průřezu (\(a=b\)) roste tuhost se čtvrtou mocninou rozměrů. Obsah (a tedy i hmotnost) roste s druhou mocninou. Uvažujme tři nosníky. První má čtvercový průřez. Druhý také, ale průřez má dvojnásobný obsah. (Strana je tedy \(\sqrt 2\)-krát delší.) Třetí nosník bude krabicový nosník. Bude mít vnější rozměry stejné jako větší nosník, ale uvnitř bude čtvercová dutina o rozměrech prvního nosníku. Tuhost prvního nosníku bude referenční, označme ji \(I\). Tuhost druhého nosníku bude čtyřnásobná, tj. \(4I\) a za toto navýšení tuhosti “platíme” použitím dvojnásobného množství materiálu. Tuhost třetího nosníku najdeme jako rozdíl prvních dvou, tj. \(3I\), protože i geometricky největší nosník vznikne zasunutím prvního nosníku do dutiny ve třetím krabicovém nosníku. Nyní porovnjeme původní nosník a krabicový nosník. Oba používají stejné množství materiálu, ale tuhost krabicového nosníku je trojnásobná. To proto, že část materiálu je dál od osy symetrie průřezu. Podobně se dá zdůvodnit a výpočtem ukázat, že profil ve tvaru písmene I, známé íčko, je tužší než tyč vykovaná ze stejného množství materiálu.
• Pro čtvercový průřez roste tuhost se čtvrtou mocninou délky strany. Podobná závislost musí být u každého průřezu jednoparametrického tvaru, například pro kruh. Jako na nosník s kruhovým průřezem můžeme pohlížet i na stromy. Například strom, ve kterém je dutina o velikosti poloviny průměru kmene většinou vyvolá obavy ze stability. I když taková dutina vypadá obrovská, tuhost se sníží o původní tuhost vynásobenou koeficientem \[(0.5)^4=0.0625\approx 6\%.\] Vidíme, že i s hrozivě vypadající dutinou má kmen pořád tuhost \(94\%\) původní tuhosti (za předpokladu dutiny uprostřed kmene). Pevnost roste jenom s třetí mocninou a proto odolnost vůči zlomení neklesne tak dramaticky jako tuhost.