Modely založené na rychlostech (derivacích)

Tepelná výměna, káva v hrnku

• Z fyziky víme, že rychlost tepelné výměny mezi dvěma tělesy je úměrná rozdílu jejich teplot (Newtonův zákon tepelné výměny). Rychlostí tepelné výměny můžeme rozumět například rychlost s jakou roste teplota studeného tělesa v teplém prostředí nebo s jakou klesá teplota horkého tělesa umístěného v chladnějším prostředí.
• Rychlost s jakou roste teplota \(T\) tělesa tělesa v čase je derivace teploty podle času. Pokud potřebujeme pracovat s poklesem, uvažujeme záporně vzatou derivaci. Úměrnost matematicky vyjádříme násobením konstantou a teplotní rozdíl může být například při umístění horkého tělesa o teplotě \(T\) v chladné místnosti o teplotě \(T_0\) vyjádřen rozdílem \(T-T_0\).
• Proces tepelné výměny probíhající podle Newtonova zákona je tedy možno modelovat vztahem \[ \frac{\mathrm dT}{\mathrm dt}=-k(T-T_0). \]
• K rovnici v ideálním případě dodáváme materiálovou charakteristiku (konstantu úměrnosti \(k\)) a počáteční teplotu. Řešením je funkce udávající závislost teploty na čase. Chceme-li znát teplotu za určitý čas, není nutné provádět pokus a čekat na uplynutí požadované doby. Můžeme teplotu přímo vypočítat.
• Někdy může být vhodné nesledovat teplotu \(T\), ale rozdíl oproti okolní teplotě, \(\tau=T-T_0\). Model se potom zjednoduší na \[ \frac{\mathrm d\tau}{\mathrm dt}=-k\tau,\] tedy na model, kdy rychlost změny je úměrná funkční hodnotě.

Radioaktivní rozpad, radon ve sklepě

• Radioaktivní prvky se rozpadají rychlostí, která je úměrná množství dosud nerozpadnutého materiálu. Rychlost, s jakou se mění množství (a tedy i koncentrace \(y\) v daném vzorku) nerozpadnutého radioaktivního materiálu je tedy popsána matematickým modelem \[\frac{\mathrm dy}{\mathrm dt}=-\lambda y,\] kde \(\lambda\) je konstanta úměrnosti. Tato rovnice je přirozeným důsledkem toho, že pro daný nestabilní izotop mají všechny atomy stejnou pravděpodobnost, že u nich dojde k rozpadu a tato pravděpodobnost se s časem nemění.
• Nejznámější aplikací této rovnice je datování archeologických vzorků pomocí radioaktivního uhlíku \(^{14}C\). V tomto případě se sleduje vzájemná relace mezi množstvím tohoto nestabilního uhlíku a množstvím stabilního \(^{12}C\). Počáteční podmínka je známa (předpokládáme stejný poměr zastoupení jako relativně nedávno, před průmyslovou revolucí) a díky tomu můžeme najít funkci udávající, jak s časem klesá zastoupení radioaktivního uhlíku. Obsah radioaktivního i stabilního uhlíku je možné změřit a tím získáme odhad, kolik procent radioaktivního uhlíku se rozpadlo. Řešení počáteční úlohy poté použijeme pro odhad doby, kdy organismus přestal spotřebovávat uhlík z atmosféry, tj. odhad stáří vzorku.
• Při pokusu o datování kostí dinosaurů klesne množství radioaktivního uhlíku pod měřitelnou úroveň. Proto se v tomto případě používají látky s delším poločasem rozpadu.
• Optikou běžného života je nejzajímavější aplikací této rovnice model rozpadu v radioaktivní radě uranu, kdy vzniká plynný radon, který může působit problémy ve stavbách a v rizikových lokalitách je potřeba vhodnými konstrukčními přístupy nebo aktivními zařízeními na lapání a odvětrávání radonu.

Samočištění jezer, kontaminace v jezeře

• Nechť veličina \(y\) udává množství látky, která znečišťuje vodu v jezeře o objemu \(V\).
• Předpokládejme, že do jezera přitéká čistá voda a stejnou rychlostí odtéká voda s nečistotami (hladina se nemění, je v ustáleném stavu). Nechť veličina \(r\) udává, jaký objem vody se v jezeře takto vymění za jeden den. Předpokládejme dále (poněkud nerealisticky), že rozdělení znečišťujících částic v jezeře je rovnoměrné.
• Úbytek hmotnosti nečistot za časovou jednotku je dán derivací \(\frac{\mathrm dy}{\mathrm dt}\).
• Protože koncentrace nečistot v jezeře a v odtékající vodě je \(\frac yV\), je úbytek znečištění možno vyjádřit též ve tvaru \(\frac rVy\). Podíl \(\frac rV\) je pro dané jezero kladná konstanta udávající, jak velká část z celkového množství vody se v jezeře vymění za časovou jednotku. Označíme-li tuto konstantu symbolem \(k\), je proces úbytku nečistot v jezeře popsán vztahem \[ \frac{\mathrm dy}{\mathrm dt} =-ky. \]
• Výše uvedený model se nazývá rovnice samočištění jezer, ale tento název je čistě formální. Jedná se vlastně o stejnou rovnici, která popisuje radioaktivní rozpad nebo změnu rozdílu mezi teplotou horkého nápoje a místnosti při chladnutí nápoje.
• Stejnou rovnicí je možné popsat nejenom odbourávání nečistot z životního prostředí, ale i odbourávání léků nebo drog z těla. Považujme krevní oběh za jezero a lék nebo drogu za znečišťující látku. V případě, že rychlost odbourávání je úměrná koncentraci (platí pro farmakokinetiku prvního řádu, toto splňuje většina léčiv za běžných koncentrací), řídí se proces odbourávání stejnou diferenciální rovnicí.

Vývoj populace a její ekologický lov

• Zkoumejme velikost \(y\) určité populace, v prostředí s nosnou kapacitou \(K\).
• Realistickým předpokladem dodaným biologickými vědami je, že v prostředí s omezenými úživnými vlastnostmi specifická míru růstu populace (rychlost s jakou se velikost populace zvětšuje vztažená na jednotkové množství populace) klesá s tím, jak se velikost populace přibližuje k nosné kapacitě, a rychlost růstu populace je modelována funkcí \(ry\left(1-\frac yK\right)\). Podle velkosti koeficientů v této funkci dělíme živočichy na r-stratégy a K-stratégy a toto dělení odráží, jak se snaží druh vyrovnávat se změnami prostředí.
• Za uvedených předpokladů je možno vývoj populace popsat modelem \[\frac{\mathrm dy}{\mathrm dt}=ry\left(1-\frac yK\right),\] který se nazývá logistická rovnice.
• Pokud lovem snížíme přírůstky populace, můžeme tento proces popsat modelem \[\frac{\mathrm dy}{\mathrm dt}=ry\left(1-\frac yK\right)-h(y),\] kde \(h(y)\) je intenzita lovu populace o velikosti \(y\). Modelování tohoto procesu umožní nalezení ekonomicky výhodné ale přitom trvale udržitelné strategie lovu.

Obyčejná diferenciální rovnice prvního řádu

Obyčejná diferenciální rovnice je rovnice, kde vystupuje neznámá funkce a její derivace. Setkáváme se s ní například všude tam, kde rychlost růstu nebo poklesu veličiny souvisí s její velikostí. Například rychlost s jakou se mění teplota horkého tělesa je funkcí teploty samotné. Rychlost tepelné výměny mezi dvěma tělesy je totiž úměrná rozdílu jejich teplot (Newtonův zákon). Takto se přirozeně diferenciální rovnice objevují v modelech nejrůznějších dějů jevů. Podstatu děje, který modelujeme, musí dodat fyzika, biologie nebo jiná aplikovaná věda. To v matematice obsaženo není. Matematika poté poslouží k analýze, jaké jsou pozorovatelné důsledky a tím se ověří, jestli příslušná aplikovaná věda správně vystihuje podstatu modelovaného děje.

Definice (diferenciální rovnice).

Obyčejnou diferenciální rovnicí prvního řádu rozřešenou vzhledem k derivaci (stručněji též diferenciální rovnicí, DR) s neznámou \(y\) rozumíme rovnici tvaru \[ \frac{\mathrm{d}y}{\mathrm{d}x}=\varphi(x,y) \tag{1}\] kde \(\varphi\) je funkce dvou proměnných.

(anglicky ordinary differential equation, ODE)

Další formy zápisu rovnice (1) jsou \[y'=\varphi(x,y),\] \[{\mathrm{d}y}=\varphi(x,y)\mathrm{d}x,\] \[{\mathrm{d}y}-\varphi(x,y)\mathrm{d}x=0.\]

Diferenciální rovnice udává scénář vývoje systému. K jednoznačnému předpovězení budoucího stavu je ovšem nutno znát nejenom, jaký mechanismus ovlivňuje vývoj systému, ale také stav současný.

Definice (počáteční podmínka, Cauchyova úloha).

Nechť \(x_0\), \(y_0\) jsou reálná čísla. Úloha najít řešení rovnice
\[ \frac{\mathrm{d}y}{\mathrm{d}x}=\varphi(x,y), \tag{1}\] které splňuje zadanou počáteční podmínku \[ y(x_0)=y_0 \tag{2}\] se nazývá počáteční (též Cauchyova) úloha.

Řešení Cauchyovy úlohy nazýváme též partikulárním řešením rovnice. Graf libovolného partikulárního řešení se nazývá integrální křivka.

(anglicky initial condition, IC, initial value problem, IVP)

Věta (existence a jednoznačnost řešení Cauchyovy úlohy).

Má-li funkce \(\varphi (x,y)\) ohraničenou parciální derivaci \(\frac{\partial \varphi}{\partial y}\) v okolí počáteční podmínky, potom má počáteční úloha (1)-(2) právě jedno řešení definované v nějakém okolí počáteční podmínky.

Obecné a partikulární řešení

Řešení diferenciální rovnice je nekonečně mnoho. Zpravidla je dokážeme zapsat pomocí jediného vzorce, který obsahuje nějakou (alespoň do jisté míry libovolnou) konstantu \(C\). Takový vzorec se nazývá obecné řešení rovnice. Pokud není zadána počáteční podmínka a mluvíme o partikulárním řešení, máme tím na mysli jednu libovolnou funkci splňující diferenciální rovnici.

Příklad: Obecným řešením diferenciální rovnice \[y'=2xy\] je \[y=Ce^{x^2}, \quad C\in\mathbb{R}.\] Žádná jiná řešení neexistují, všechna řešení se dají zapsat v tomto tvaru pro nějakou vhodnou konstantu \(C\). Partikulárním řešením je například \(y=5e^{x^2}\). Řešením počáteční úlohy \[y'=2xy, \quad y(0)=3\] je \[y=3e^{x^2}.\]

Úvod do problematiky numerického řešení diferenciálních rovnic

Nejprve si naznačíme možnosti numerického řešení. To vychází z grafické interpretace diferenciální rovnice a odpovídá v podstatě modelování, kdy postupně prodlužujeme řešení od zadané počáteční podmínky dopředu či dozadu v čase. Přitom musíme řešit situaci vždy pro konkrétní numerické hodnoty počáteční podmínky a všech parametrů. Naštěstí se dá vhodnou transformací (resp. vhodnou volbou jednotek) počet parametrů zredukovat a tím se zvýší obecná použitelnost numerického výpočtu.

Geometrická interpretace ODE

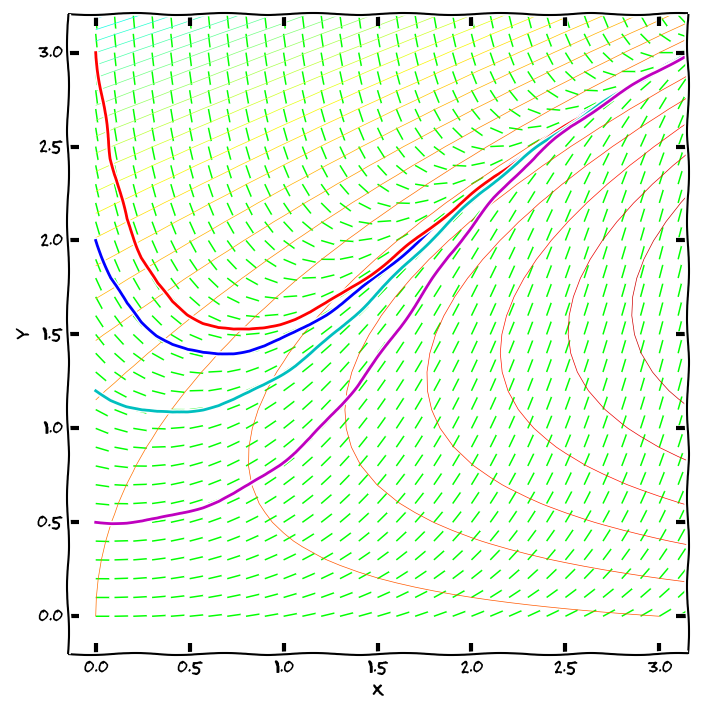
Protože derivace funkce v bodě udává směrnici tečny ke grafu funkce v tomto bodě, lze rovnici \[y'=\varphi(x,y)\] chápat jako předpis, který každému bodu v rovině přiřadí směrnici tečny k integrální křivce, která tímto bodem prochází. Sestrojíme-li v dostatečném počtu (například i náhodně zvolených) bodů \([x,y]\) v rovině vektory \((1,\varphi(x,y))\), obdržíme směrové pole diferenciální rovnice — systém lineárních elementů, které jsou tečné k integrálním křivkám.

Počáteční podmínka \(y(x_0)=y_0\) geometricky vyjadřuje skutečnost, že graf příslušného řešení prochází v rovině bodem \([x_0,y_0]\). Má-li tato počáteční úloha jediné řešení, neprochází bodem \([x_0,y_0]\) žádná další křivka. Má-li každá počáteční úloha jediné řešení (což bude pro nás velice častý případ), znamená to, že integrální křivky se nikde neprotínají.

Křivky s konstantní hodnotou \(\varphi(x,y)\) mají tu vlastnost, že je všechna řešení protínají pod stejným úhlem, měřeným od kladné části osy \(x\). Například v bodech kde platí \(\varphi(x,y)=0\) míří všechny integrální křivky vodorovně. Proto se křivky, kde je \(\varphi(x,y)\) konstantní, nazývají izokliny.

Numerické řešení IVP

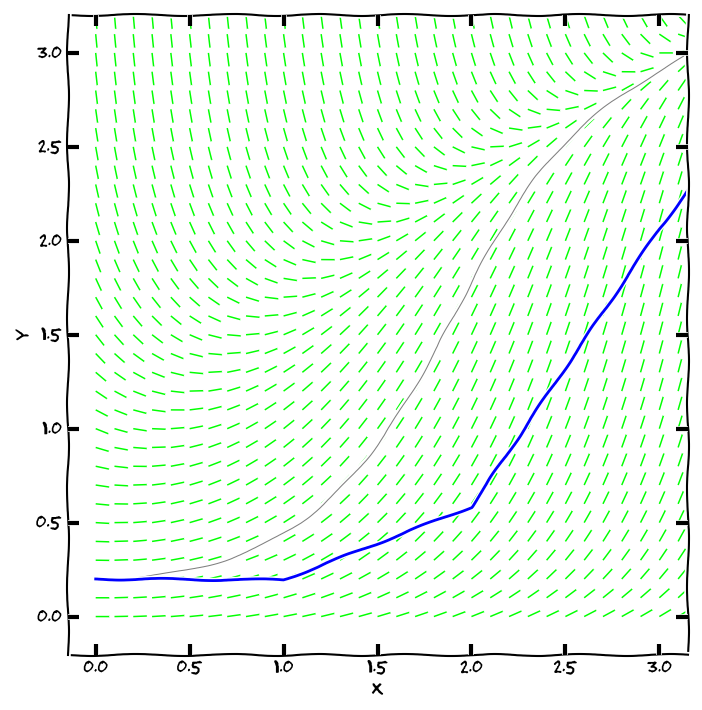
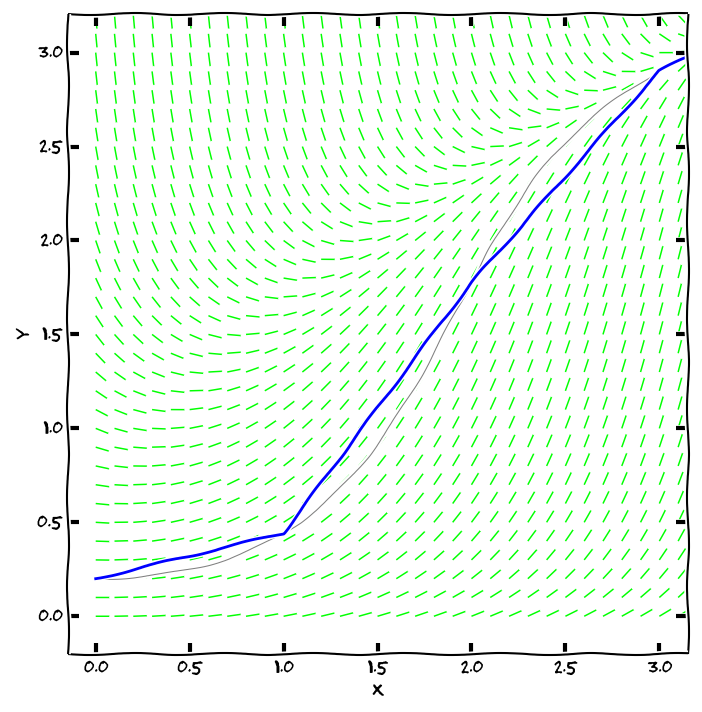
Řešení počáteční úlohy lze numericky aproximovat poměrně snadno: začneme v bodě zadaném počáteční podmínkou a v okolí tohoto bodu nahradíme integrální křivku její tečnou. Tím se dostaneme do dalšího bodu, odkud opět integrální křivku aproximujeme tečnou. Směrnici tečny zjistíme z diferenciální rovnice, buď přímo z derivace (Eulerova metoda).

Vyjdeme-li z počáteční úlohy \[y'=\varphi(x,y), \quad y(x_0)=y_0,\] má lineární aproximace řešení v bodě \([x_0,y_0]\) tvar \[y=y_0+\varphi(x_0,y_0)(x-x_0).\] Funkční hodnotu v bodě \(x=x_1\) označíme \(y_1\) a tento bod bude dalším body lomené čáry, tj. \[y_1=y_0+\varphi(x_0,y_0)(x_1-x_0).\] Hodnota \(x_1-x_0\) je krok Eulerovy metody označovaný \(h\). Tento postup opakujeme s počáteční podmínkou \(y(x_1)=y_1\). Iterační formule Eulerovy metody má potom následující tvar. \[\begin{aligned}x_{n+1}&=x_n+h, \\ y_{n+1}&=y_n+\varphi(x_n,y_n)h.\end{aligned}\]

Stačí tedy mít zvolen krok numerické metody (délku intervalu, na kterém aproximaci tečnou použijeme) a výstupem metody bude aproximace integrální křivky pomocí lomené čáry.

Vylepšení

• Pro přesnější aproximaci je možné zjemnit krok \(h\) (buď všude, nebo jenom tam, kde “je to potřeba”).
• Pro přesnější aproximaci je možné použít místo \(\varphi(x_n,y_n)\) lepší směrnici, která dokáže zohlednit, jestli se růst zrychluje nebo zpomaluje (metoda Runge Kutta druhého nebo čtvrtého řádu, …).
• Modely obsahující diferenciální rovnice obsahují zpravidla sadu parametrů charakterizujících fyzikální vlastnosti studovaných objektů. Pro numerické řešení musíme těmto parametrům dát konkrétní hodnoty a přicházíme tak o cennou informaci, jak řešení závisí na těchto parametrech. Vhodnou úpravou rovnice dokážeme počet parametrů eliminovat. Jednoduchým a často dostatečným způsobem je volba jednotek, obecnější metodou je transformace diferenciální rovnice uvedená v následujícím textu.

Online řešiče ODE (numericky):

• Sage
• Python

ODE tvaru \(\frac{\mathrm dx}{\mathrm dt}=f(x)\)

Rovnice \[\frac{\mathrm dx}{\mathrm dt}=f(x)\tag{♣}\] se nazývá autonomní, nebo též nezávislá na čase. Je speciálním případem rovnice se separovanými proměnnými, která je uvedena na dalším slidu a naučíme se ji řešit analytickou cestou. Proto se nyní nebudeme zaměřovat na hledání obecného řešení, ale pokusíme se popsat chování řešení, aniž bychom tato řešení znali. Pokusíme se s co nejmenší námahou říct, jak se budou řešení chovat.

• Je-li \(f(x_0)=0\), je konstantní funkce \(x(t)=x_0\) řešením rovnice (♣). Protože derivace konstantní funkce je nula, vidíme, že řešením rovnice \[f(x)=0\] obdržíme všechna konstantní řešení rovnice (♣).
• Konstantní řešení představují rovnovážný stav. Často nás zajímá, jestli při vychýlení z tohoto rovnovážného stavu má systém tendenci se vrátit do původního stavu, nebo se od původního stavu dále odchylovat. Na tuto otázku dává odpověď následující věta.

Věta (stabilita konstantních řešení).

Jestliže platí \(f(x_0)=0\), je konstantní funkce \(x(t)=x_0\) konstantním řešením rovnice \[\frac{\mathrm dx}{\mathrm dt}=f(x).\] Toto řešení je stabilní pokud \(f'(x_0)<0\) a nestabilní pokud \(f'(x_0)>0\).

Pro grafickou intepretaci je vhodné připomenout, že funkce s kladnou derivací jsou rostoucí a funkce se zápornou derivací klesající. Pokud má tedy pravá strana derivaci různou od nuly, poznáme stabilitu z monotonie pravé strany.

Autonomní rovnice s pravou stranou ve tvaru rozdílu

Poznámka (autonomní rovnice s rozdílem na pravé straně).

Rovnice \[\frac{\mathrm dx}{\mathrm dt}=g(x)-h(x)\] má stacionární bod \(x_0\), jestliže \[g(x_0)=h(x_0).\] Často jsou funkce \(g\) a \(h\) zadány graficky a stacionární bod je v průsečíku grafů funkcí \(g\) a \(h\). Ze vzájemné polohy těchto grafů také vidíme, zda je stacionární bod stabilní (funkce \(g\) je napravo od bodu \(y_0\) pod funkcí \(h\) a nalevo nad ní) nebo nestabilní (naopak).

Příklad. Logistická diferenciální rovnice s konstantním lovem \(h\), tj. rovnice \[\frac{\mathrm dx}{\mathrm dt}=rx\left(1-\frac xK\right)-h,\] má pro malé \(h\) dva stacionární body. Funkce \(rx\left(1-\frac xK\right)\) je parabola otočená vrcholem nahoru a s nulovými body \(x=0\) a \(x=K\). V prvním stacionárním bodě je funkce rostoucí a tento stacionární bod je nestabilní. Ve druhém stacionárním bodě je funkce klesající a tento stacionární bod je stabilní. Jak se zvyšuje faktor \(h\), graf paraboly se posouvá směrem dolů a oba stacionární body se posouvají směrem k sobě a k  vrcholu. Jejich stabilita zůstává neporušena. To znamená, že sice pořád existuje stabilní stav, ale se zvyšující se intenzitou lovu se tento stacionární stav dostává stále blíže ke stavu nestacionárnímu a rovnováha je tedy poněkud křehká.

Transformace diferenciální rovnice

Prezentace

Naučíme se vyjadřovat diferenciální rovnici v jiných proměnných tak, aby bylo možné snížit počet parametrů v této rovnici. Pro jednoduchost budeme uvažovat jenom případ, kdy nová proměnná je lineární funkcí původní proměnné.

Uvažujme funkci \(y\) proměnné \(x\). Připomeneme si vzorce pro derivaci součtu, derivaci konstantního násobku a derivaci složené funkce, ale uvedeme si je v kontextu vhodném pro studium diferenciálních rovnic.

• Z derivace součtu a z derivace konstanty plyne pro funkci \(y\) a konstantu \(y_0\) vztah \[ \frac{\mathrm d (y\pm y_0)}{\mathrm dx} = \frac{\mathrm d y}{\mathrm dx} \pm \frac{\mathrm d y_0}{\mathrm dx} = \frac{\mathrm d y}{\mathrm dx} \pm 0= \frac{\mathrm d y}{\mathrm dx}.\]
• Z derivace konstantního násobku funkce plyne pro funkci \(y\) a konstantu \(k\) vztah \[ \frac{\mathrm d (ky)}{\mathrm dx} = k\frac{\mathrm d y}{\mathrm dx}.\]
• Z derivace složené funkce plyne pro konstantu \(k\) a veličinu \(X = kx\) vztah \[ \frac{\mathrm d y}{\mathrm d x} = \frac{\mathrm d y}{\mathrm dX} \frac{\mathrm d X}{\mathrm dx} = \frac{\mathrm d y}{\mathrm d X} k \] tj. \[ \frac{\mathrm d y}{\mathrm d (kx)} = \frac{\mathrm d y}{\mathrm d X} = \frac 1k \frac{\mathrm d y}{\mathrm d x}.\]

Výše uvedené výpočty je možno shrnout do pravidla v následující poznámce.

Poznámka (transformace diferenciální rovnice do jiných jednotek).

Pro \(Y=k_1(y-y_0)\) a \(X=k_2 x\) platí \[ \frac{\mathrm d Y}{\mathrm d X} = \frac{\mathrm d \Bigl(k_1(y-y_0)\Bigr)}{\mathrm d (k_2 x)} = \frac{k_1}{k_2} \frac{\mathrm dy}{\mathrm dx}\] a podobně (všimněte si druhé mocniny u \(k_2\) díky druhé derivaci) \[ \frac{\mathrm d^2 Y}{\mathrm d X^2} = \frac{k_1}{k_2^2} \frac{\mathrm d^2y}{\mathrm dx^2}.\] Výraz nalevo neobsahuje konstanty, které jsou ve výrazu napravo. Tyto konstanty jsou v definici nových veličin \(X\) a \(Y\).

Navíc vzorec z poznámky silně připomíná klasické počítání se zlomky. Proto máme Leibnizův tvar zápisu derivací \(\frac{\mathrm dy}{\mathrm dx}\) při studiu diferenciálních rovnic více v oblibě, než zápis Lagrangeův, \(y'\).

Příklad. Diferenciální rovnice tepelné výměny \[\frac{\mathrm dT}{\mathrm dt}=-k(T-T_\infty), \quad T(0)=T_0\tag{*}\] obsahuje tři parametry: teplotu okolního prostředí \(T_\infty\), počáteční teplotu \(T_0\) a konstantu \(k\) související s fyzikálními vlastnostmi prostředí. Postupně můžeme posunout teplotní stupnici tak, aby teplota okolí byla nula a počáteční teplota jedna, tj. hodnotu \(T\) snížíme o \(T_\infty\) a upravíme dílek stupnice \((T_0-T_\infty)\)-krát \[\frac{\mathrm d\left(\frac{T-T_\infty}{T_0-T_\infty}\right)}{\mathrm dt}=-k\frac{T-T_\infty}{T_0-T_\infty}\] vydělit konstantou \(k\) \[\frac{\mathrm d\left(\frac{T-T_\infty}{T_0-T_\infty}\right)}{k\mathrm dt}=-\frac{T-T_\infty}{T_0-T_\infty}\] a přeškálovat pomocí konstanty \(k\) čas \[\frac{\mathrm d\left(\frac{T-T_\infty}{T_0-T_\infty}\right)}{\mathrm d(kt)}=-\frac{T-T_\infty}{T_0-T_\infty}.\] Po substituci \(\tau=\frac{T-T_\infty}{T_0-T_\infty}\), \(\theta=kt\) má úloha tvar \[\frac{\mathrm d \tau}{\mathrm d \theta}=-\tau,\quad \tau(0)=1. \tag{**}\] Nová rovnice (**) neobsahuje žádné parametry a proto je pro studium jednodušší. Přesto je v ní obsažena veškerá informace obsažená v rovnici (*). Tuto informaci je však nutno interpretovat v kontextu definice nových proměnných. Například to, že všechna řešení rovnice (**) konvergují k nule znamená, že všechna řešení rovnice (*) konvergují k \(T_0\). To, že řešení rovnice (**) klesne na poloviční hodnotu za čas \(\ln 2\) znamená, že vzdálenost řešení rovnice (*) od rovnovážného stavu se na polovinu zmenší za čas \(\frac 1k \ln 2\).

Poznámka (nondimenzinalizace, rozměrová analýza).

Proces eliminace parametrů z modelu popsaného diferenciální rovnicí se nazývá nondimenzionalizace nebo rozměrová analýza modelu, protože eliminaci parametrů je vhodné provádět tak, aby výsledné nové veličiny vycházely bez fyzikálních jednotek. K tomu se provádí rozbor jednotek jednotlivých veličin. V jednoduchých případech však stačí primitivní postup popsaný v odstavcích výše a ukázaný na příkladu. V tomto příkladě veličina \(x\) nemá fyzikální jednotku, protože je součinem konstanty \(k\) (s jednotkou \(\mathrm s^{-1}\)) a času \(t\) (s jednotkou \(\mathrm s\)). Je možné ji považovat za bezrozměrný čas. Veličina \(y\) také nemá fyzikální jednotku, protože je podílem dvou teplot a je možné ji považovat za bezrozměrnou teplotu.

V této úloze bylo zavedení nových veličin přirozené. I u méně zřejmých úloh zkušenosti ukazují, že je vhodné volit transformaci tak, aby vznikly veličiny bezrozměrné, které nemají fyzikální jednotku. Například v Horáček, Fyzikální a mechanické vlastnosti dřeva I je zavedena bezrozměrná vlhkost, bezrozměrný čas a bezrozměrná vzdálenost na straně 61 pro rovnici popisující difuzi a charakteristická délka, Biotovo číslo (bezrozměrná tepelná vodivost) a bezrozměrná teplota, bezrozměrný čas a bezrozměrná vzdálenost pro rovnici popisující vedení tepla na stranách 88 a 89.