Opakování

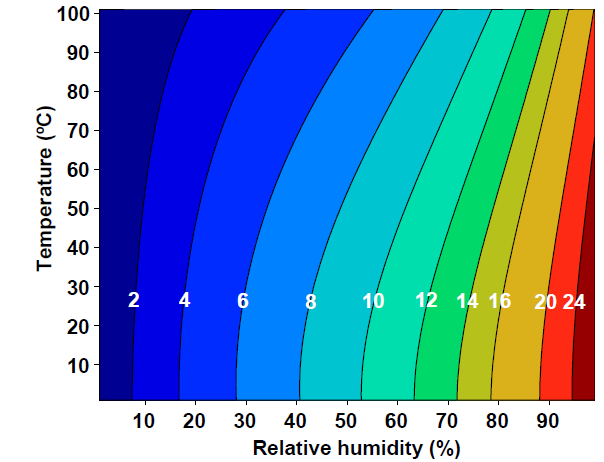
Vrstevnice

• Pro funkci dvou proměnných jsou vrstevnice křivky, které spojují místa se stejnou funkční hodnotou.

Lineární algebra

• Součin matice a vektoru je lineární kombinace sloupců matice, přičemž koeficienty této kombinace jsou složky vektoru. Viz následující příklad. \[\begin{pmatrix}2 & 1\\-1 &3 \end{pmatrix} \begin{pmatrix}2\\3\end{pmatrix} = 2\begin{pmatrix}2\\-1\end{pmatrix} + 3\begin{pmatrix}1\\3\end{pmatrix} = \begin{pmatrix}7\\7\end{pmatrix}\]
• Matice je možno chápat jako zobrazení mezi vektorovými prostory. Vektor můžeme pomocí matice zobrazit na jiný vektor. Zachovávají se přitom důležité vlastnosti, jako se přitom rovnoběžnost a poloha středu úsečky.
• Matice je možno použít pro přepočet vektorů a tenzorů do jiné soustavy souřadnic.
• Pokud se vektor zobrazí na svůj násobek, nazývá se vlastní vektor a tento násobek je vlastní číslo. \[A\vec v=\lambda \vec v\]
• Matice s vlastními vektory se směru souřadných os je diagonální. Skutečně, například použitím definice maticového součinu a použitím definice vlastního vektoru a čísla dostáváme \[\begin{pmatrix}a & b\\c &d \end{pmatrix} \begin{pmatrix}1\\0\end{pmatrix} = \begin{pmatrix}a\\c\end{pmatrix}\quad\text{a}\quad \begin{pmatrix}a & b\\c &d \end{pmatrix} \begin{pmatrix}1\\0\end{pmatrix}=\lambda \begin{pmatrix}1\\0\end{pmatrix}.\] To si vynutí \(c=0\). Podobně bychom dostali pro vektor ve směru druhé osy \(b=0\).
• Pro matici \[A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}\] a vektory \[\vec u= \begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix}, \qquad \vec v= \begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix}\] platí \(\vec v = A\vec u\) jestliže \[ \begin{aligned} v_1=a_{11}u_{1}+a_{12}u_2+a_{13}u_3\\ v_2=a_{21}u_{1}+a_{22}u_2+a_{23}u_3\\ v_3=a_{31}u_{1}+a_{32}u_2+a_{33}u_3. \end{aligned} \] Toto je možno zapsat jedinou rovnicí \[ v_i=a_{i1}u_{1}+a_{i2}u_2+a_{i3}u_3 \] kde index \(i\) probíhá hodnoty od jedné do tří. Součet na pravé straně je možno zapsat v sumační symbolice \[ v_i=\sum_{j=1}^3a_{ij}u_{j}. \] Obvyklým zjednodušením je, že se vynechává znak součtu a automaticky se sčítá přes opakující se index, který figuruje napravo, ale nefiguruje nalevo. Zápis maticového součinu se potom formálně zjednoduší na \[ v_i=a_{ij}u_{j} \] a toto označení se nazývá Einsteinova sumační symbolika.

Animace

Diferenciální operátory

Parciální derivace se vyskytují ve většině důležitých rovnic popisujících fyzikální svět okolo nás. Vztahy ze středoškolské fyziky nebo tabulek pro inženýry jsou jenom důsledky odvozené pro hodně speciální situace. Všude tam, kde se zajímáme o fyzikální podstatu děje a máme ambice popsat děj přesně, nestačí středoškolský aparát, protože je nutné pracovat s okamžitou rychlostí změn fyzikálních veličin. A tyto jsou vyjádřeny právě parciálními derivacemi.

Parciální derivace umožňují sledovat závislost stavových veličin v závislosti na souřadnicích nebo čase, a to pro každou souřadnici samostatně. Nicméně souřadný systém je něco, co do popisu vnášíme uměle a proto by fyzikální proces neměl být na tomto souřadném systému závislý. Proto často spojujeme parciální derivace do složitějších výrazů – diferenciálních operátorů. Zde teprve vynikne síla parciálních derivací.

Gradient

Definice (gradient).

Gradient skalární funkce dvou proměnných \(f(x,y)\) je vektorové pole označené a definované následovně. \[\nabla f=\left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)\] Podobně je definován gradient skalární funkce tří proměnných \(f(x,y,z)\). \[\nabla f=\left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\right)\]

Význam a postavení gardientu ilustruje následující příklad, který je poté zobecněn do poznámky shrnující fyzikální význam gradientu.

Příklad. Pokud je teplota v rovině v bodě \((x,y)\) dána předpisem \[T=(x^2-xy^2)^\circ\mathrm C,\] je gradientem vektor \[\nabla T=\begin{pmatrix}2x-y^2, -2xy\end{pmatrix} {}^\circ\mathrm C \mathrm m^{-1}.\] V bodě \((1,1)\) je gradient \[\nabla T(1,1)=\begin{pmatrix}1,-2\end{pmatrix}{}^{\circ}\mathrm C \mathrm m^{-1}.\] To znamená, že v tomto bodě roste teplota ve směru osy \(x\) rychlostí jeden stupeň Celsia na každý metr délky a ve směru osy \(y\) klesá rychlostí dva stupně Celsia na každý metr délky. Vektor definovaný tímto gradientem má směr doprava dolů (pod úhlem splňujícím podmínku \(\tan \varphi = -2\)) a délku \(\sqrt{(1)^2+(-2)^2}=\sqrt 5\approx 2.2\). To znamená, že maximální nárůst teploty je směrem doprava dolů a tento nárůst je \(2.2\) stupně Celsia na každý metr délky.

Poznámka (fyzikální význam gradientu).

Gradient skalární veličiny \(f\) je vektorová veličina, která vyjadřuje směr a intenzitu maximálního růstu veličiny \(f\). Přesněji, výsledkem gradientu je vektor ve směru maximálního růstu veličiny \(f\). Délka tohoto vektoru je nárůst veličiny \(f\) na intervalu jednotkové délky. Pro rovnoměrně rozloženou veličinu v prostoru (konstantní) je gradient nulový. Proto je možné gradient chápat jako míru nerovnoměrného rozložení veličiny v prostoru. Řada fyzikálních dějů probíhá tak, že tato nerovnoměrnost vyvolá proudění, které se snaží tuto nerovnoměrnost vyrovnat. Například vedení tepla vyrovnává nerovnoměrné rozložení teploty a difuze vyrovnává nerovnoměrnosti v koncentraci. Teplota se vyrovnává tak, že teplo teče z místa s vysokou teplotou do místa s malou teplotou. Difuze směřuje z místa s vyšší koncentrací do místa s nižší koncentrací. V praxi nás proto většinou místo směru maximálního růstu zajímá směr maximálního poklesu, tj. \(-\nabla f\).

Symbol \(\nabla\) je operátor nabla definovaný formálně vztahem \[\nabla=\left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right)\] nebo \[\nabla=\left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}\right)\] (v závislosti na počtu proměnných funkce \(f\)). “Násobení” \(\frac{\partial }{\partial x}\) s funkcí \(f\) přitom chápeme jako parciální derivaci \(\frac{\partial f}{\partial x}\).

Někdy je vhodné formulovat fyzikální zákony pomocí prostředků lineární algebry, zejména pomocí maticového součinu. V takovém případě gradient zapisujeme jako sloupcový vektor.

Gradient úzce souvisí s vrstevnicemi, s křivkami, které spojují místa se stejnou funkční hodnotou funkce dvou proměnných. Někdy místo pojmu vrstevnice používáme výraz, který obsahuje i povahu sledované veličiny, například se používají názvy jako izotermy, izobary, hydroizopsy, hydroizopiezy atd. Pro funkce tří proměnných máme plochy spojující místa se stejnou funkční hodnotou ekvipotenciální plochy. Gradient je v každém bodě kolmý k vrstevnici (ve 2D) resp. k ekvipotenciální ploše (ve 3D). Nakreslit online.

Gradient v přírodě

• V matematice se gradientem rozumí vektor z parciálních derivací podle všech proměnných. V aplikacích tomu bývá poněkud jinak. Často je funkce popisující studovaný systém funkcí času i prostorových proměnných. V takovém případě gradientem rozumíme vektor složený jenom z parciálních derivací podle prostorových proměnných. Čas při výpočtu gradientu za proměnnou nepovažujeme.
• V jednorozměrném případě je gradient totéž co derivace. Přesto se někdy z tradičních důvodů respektujících zvyklosti oboru nemluví o derivaci, ale o gradientu. Například mluvíme o gradientu teploty při studiu tepelně izolačních vlastností materiálů. Pokud máme na mysli vrstvu z jednoho materiálu (a ne například sendvičovou stěnu), je rozložení teploty lineární a dokonce v tomto případě pojmem gradient vlastně označujeme směrnici přímky.
• S gradientem souvisí majáková navigace při migraci živočichů. Ti sledují určitý chemický podnět a pohybují se ve směru největšího růstu tohoto podnětu. Tedy ve směru gradientu. Například žralok ve vodě takto sleduje koncentraci krve.
• Pokud se zajímáme nejenom o směr, ale i velikost gradientu, pomůže nám velikost gradientu k posouzení rychlosti změny veličiny v prostoru (gradient je velký, jestliže se funkce mění rychle a jsou-li tím pádem vrstevnice nahusto).
• Při proudění podzemní vody sledujeme hydroizohypsy, křivky spojující místa se stejnou hladinou podzemní vody nebo obecněji se stejnou piezometrickou výškou. Tok vody je v homogenním prostředí kolmý na tyto křivky a intenzivní podle hustoty křivek. Zjednodušeně řečeno, i podzemní voda má snahu téct “z kopce”, ale “z kopce” je ve smyslu nejrychlejšího poklesu piezometrické výšky. Anizotropní prostředí tento tok může odklánět do směru, ve kterém půda klade toku podzemní vody menší odpor. Podobně jako dřevo stáčí tok tepla nebo vlhkosti do podélného směru.

Lineární aproximace

S lineární aproximací jsme se seznámili již dříve. Ukážeme si spojitost s gradientem.

Lineární aproximace skalární funkce jedné proměnné

\[f(x)\approx f(x_0)+f'(x_0)(x-x_0)\] Rychlost růstu je vyjádřena derivací.

Lineární aproximace skalární funkce více proměnných

\[ f(x,y)\approx f(x_0, y_0)+ \nabla f(x_0,y_0)\cdot (x-x_0,y-y_0)\] V tomto případě je derivace nahrazena gradientem.

Lineární aproximace vektorové funkce

\[\vec F(x,y)\approx \vec F(x_0,y_0) + J(x_0,y_0) \begin{pmatrix}x-x_0\\ y-y_0\end{pmatrix}\] V tomto případě je derivace nahrazena Jacobiho maticí \[J(x,y)=\begin{pmatrix} \frac{\partial f_1}{\partial x}(x ,y ) & \frac{\partial f_1}{\partial y}(x ,y )\\\frac{\partial f_2}{\partial x}(x ,y ) & \frac{\partial f_2}{\partial y}(x ,y )\end{pmatrix},\] kde \(f_1\) a \(f_2\) jsou komponenty vektorové funkce \(\vec F\). Řádky Jacobiho matice jsou tvořeny gradientem jednotlivých složek vektorové funkce \(\vec F\).

Obecné vícerozměrné konstitutivní zákony

Konstitutivní vztahy tvoří z hlediska materiálového inženýrství jednu z nejdůležitějších aplikací gradientu. Tyto vztahy dávají do vzájemné relace gradient stavové veličiny, pomocí níž charakterizujeme stav studovaného objektu, a tok, který se snaží zahladit nerovnoměrnost v rozložení stavové veličiny. Například při nerovnoměrném rozložení koncentrace látky se tato koncentrace vyrovnává difuzním tokem. Při nerovnoměrném rozložení vnitřní energie v systému se tato nerovnoměrnost navenek projevuje rozdílnými teplotami v různých částech tělesa a vyrovnává tokem tepla. Při různých piezometrických hladinách podzemní vody (hladina podzemní vody se započtením případného tlaku a dalších parametrů majících vliv na proudění vody) se tato nerovnoměrnost vyrovnává prouděním podzemní vody.

Speciální případy vztahu mezi gradientem a tokem

Animace

Uvažujme vztah mezi gradientem a tokem ve tvaru \[\vec j=-K\nabla u ,\] kde \(K\) je symetrický tenzor. Gradient má ve trojrozměrném případě vyjádření \[\nabla u =\left(\frac{\partial u }{\partial x},\frac{\partial u }{\partial y},\frac{\partial u }{\partial z}\right)^T\] a ve 2D \[\nabla u =\left(\frac{\partial u }{\partial x},\frac{\partial u }{\partial y}\right)^T.\]

Obecný případ (anizotropní)

Všechny konstitutivní zákony mají stejnou strukturu, kdy podnět je gradientem stavové veličiny. Tento podnět vyvolá tok a velikost toku určíme z velikosti podnětu pomocí lineární aproximace případné nelineární funkci. Roli materiálové konstanty tedy hraje maticová veličina \[K= \begin{pmatrix} k_{11}& k_{12} & k_{13}\\ k_{21}& k_{22} & k_{23}\\ k_{31}& k_{32} & k_{33} \end{pmatrix} \] jejíž komponenty zpravidla splňují \(k_{ij}=k_{ji}\). Často jsou všechny veličiny kladné a prvky v hlavní diagonále jsou dominantní.

Komponenty vektoru \(\vec j=(j_x, j_y, j_z)^T\) jsou \[ \begin{aligned} j_x&=-k_{11}\frac{\partial u }{\partial x}-k_{12}\frac{\partial u }{\partial y}-k_{13}\frac{\partial u }{\partial z},\\ j_y&=-k_{21}\frac{\partial u }{\partial x}-k_{22}\frac{\partial u }{\partial y}-k_{23}\frac{\partial u }{\partial z},\\ j_z&=-k_{31}\frac{\partial u }{\partial x}-k_{32}\frac{\partial u }{\partial y}-k_{33}\frac{\partial u }{\partial z}, \end{aligned} \] což zjistíme prostým maticovým násobením. Prostor pro další úpravu není.

Formálně je možno použitím Einsteinovy sumační symboliky a použitím souřadnic \(x_1\), \(x_2\) a \(x_3\) místo \(x\), \(y\) a \(z\) psát tuto trojici vztahů ve tvaru \[j_i = - k_{ij}\frac{\partial u}{\partial x_j}. \]

Ortotropní případ, vhodně zvolené osy

V obecném případě je zpravidla možné transformovat soustavu souřadnic tak, aby tenzor \(K\) byl diagonální. Pokud je studovaný problém ortotropní, má charakteristické směry (přesněji, má tři roviny symetrie materiálových vlastností), bude tato diagonalita tenzoru \(K\) v případě, že zvolíme souřadnice v souladu s těmito charakteristickými směry.

\[K= \begin{pmatrix} k_{11}& 0 & 0\\ 0& k_{22} & 0\\ 0& 0 & k_{33} \end{pmatrix} \]

Komponenty vektoru \(\vec j\) jsou potom dány vztahy \[ \begin{aligned} j_x&=-k_{11}\frac{\partial u }{\partial x},\\ j_y&=-k_{22}\frac{\partial u }{\partial y},\\ j_z&=-k_{33}\frac{\partial u }{\partial z}. \end{aligned} \]

Formálně je možno použitím Einsteinovy sumační symboliky a použitím souřadnic \(x_1\), \(x_2\) a \(x_3\) místo \(x\), \(y\) a \(z\) psát tuto trojici vztahů ve tvaru \[j_i = - k_{ii}\frac{\partial u}{\partial x_i}. \]

S diagonální maticí se pracuje velmi dobře, protože má v hlavní diagonále vlastní čísla. Tato vlastní čísla jsou fyzikální charakteristikou úlohy. Například největší vlastní číslo a odpovídající vlastní směr charakterizují směr, ve kterém je odezva materiálu na vnější podnět maximální a vlastní číslo udává velikost této reakce. Tyto fyzikální charakteristiky nemohou být závislé na volbě souřadné soustavy, ve které úlohu popisujeme. Co se mění s volbou souřadné soustavy jsou pouze souřadnice vlastního vektoru. Vlastní čísla jsou však skalární a proto jsou invariantní při otočení soustavy souřadnic. Pokud bychom neměli možnost zvolit soustavu souřadnic tak, aby matice byla diagonální, máme alespoň jistotu, že vlastní čísla zůstanou stejná.

Ortotropní případ ve 2D

Stejné jako ve 3D, pouze chybí třetí rovnice.

Izotropní případ

Stejné jako ortotropní případ, ale navíc platí \(k_{11}=k_{22}=k_{33}=k.\) Potom \(\vec j=-k\nabla u\), kde \(k\) je konstanta a vektory toku a gradientu mají opačný směr. V tomto případě, na rozdíl od ortotropního případu, nezávisí na volbě souřadné soustavy, tenzor materiálových vlastností se redukuje na jednorozměrnou konstantu v libovolné souřadné soustavě. Toto je nejjednodušší případ. Proto je studium izotropních materiálů mnohem mnohem jednodušší, než studium materiálů obecnějších. To je nejzásadnější vlastnost, která činí studium biologických materiálů mnohem komplikovanějším, než je třeba studium vlastností kovů. Biologické materiály mají typicky určitou vnitřní strukturu, která jim dává v různých směrech různé vlastnosti. Postupy odvozené pro izotropní materiály zde nefungují.

Konkrétní konstitutivní zákony

Fourierův zákon (vedení tepla)

Animace

Fourierův zákon udává tok tepla vyvolaný teplotním gradientem. Je to velmi používaný zákon a proto má několik variant. Budeme postupovat od nejvíce zjednodušené k nejobecnější. Ta nejobecnější nás pochopitelně zajímá.

• Jednodimenzionální tvar, kde se nezohledňuje směr toku tepla ani rozložení teploty je \[q=\lambda \frac{\Delta T}{\Delta x},\] kde \(\lambda\) je materiálová konstanta, \(q\) je tok tepla, \(\Delta T\) je teplotní rozdíl na vrstvě materiálu tloušťky \(\Delta x\). Toto je nejjednodušší tvar, umožňující základní výpočty i aparátem střední školy, jako například teplotní ztráty stěnou.
• Zohledníme-li v předešlé formulaci i směr toku tepla (proti růstu teploty, tj. z horkého místa do místa studeného), má Fourierův zákon tvar \[q=-\lambda \frac{\Delta T}{\Delta x}.\]
• Zohledníme-li v předešlé formulaci i možnost, že teplotní profil je nerovnoměrný, musíme změnu teploty počítat derivací místo podílu a poté má Fourierův zákon tvar \[q=-\lambda \frac{\mathrm d T}{\mathrm d x}.\]
• Chceme-li v předešlé formulaci zachytit i vedení tepla v rovinném materiálu či v trojrozměrném tělese, musíme derivaci teploty nahradit gradientem a poté má Fourierův zákon tvar \[\vec q=-\lambda \nabla{T}.\] V souřadnicích potom \[ q_i=-\lambda \frac{\partial T}{\partial x_i}.\]
• Chceme-li v předešlé formulaci zachytit i vedení tepla v anizotropním materiálu (v různých směrech různé vlastnosti), má Fourierův zákon formálně opět tvar \[\vec q=-\lambda \nabla{T},\] ale veličina \(\lambda\) už není skalární veličina, ale matice. V souřadnicích potom \[ q_i=-\lambda_{ij} \frac{\partial T}{\partial x_j}.\]

Veličina \(\lambda\) se nazývá součinitel tepelné vodivosti, koeficient tepelné vodivosti nebo Fourierův koeficient. Pro anizotropní materiály je tenzorová (maticová).

Fickův zákon (difuze)

V roce 1855 německý lékař A. Fick objevil, že difuzní tok \(\vec J\) (množství látky které projde při difuzi jednotkovou plochou za jednotku času) je úměrný gradientu koncentrace \(c\) této látky. Vyjádřeno moderní terminologií to znamená, že platí \[\vec J=-D\nabla c. \] Veličina \(D\) se nazývá difuzní koeficient. Pokud má \(\vec J\) stejný směr jako \(\nabla c\), je \(D\) skalární veličina. Pokud směry nejsou stejné, je \(D\) tenzor. Z fyzikálních důvodů je tenzor \(D\) symetrický.

Difuzí se například dřevo zbavuje vlhkosti při vysoušení.

Soretův efekt (termodifuze)

Většinou je hybatelem transportního děje nerovnoměrnost v rozložení té stejné veličiny, která se tímto dějem transportuje. Například tok tepla (vnitřní energie) je vyvolaný nerovnoměrným rozložením vnitřní energie, kterou vyjadřujeme pohodlněji pomocí teplotu. Nebo difuze chemické látky je vyvolána nerovnoměrným rozložením koncentrace této látky. Nemusí tomu však být vždy. Příkladem je termodifuze, což je pohyb prvků vyvolaný nerovnoměrným rozložením teploty. Například při difúzi vody ve dřevě s nerovnoměrným rozložením teploty je tok dán vztahem \[\vec J=-D\nabla c - sD\nabla T, \] kde \(s\) je koeficient termodifuze.

Rozeznáváme kladný a záporný Soretův efekt. Při kladném dochází k transportu ve směru klesající teploty, při záporném naopak ve směru rostoucí teploty. To je v kontrastu s ostatními konstitutivními zákony, kde tok stavové veličiny směřuje vždy jenom do míst s menší hustotou stavové veličiny. Viz Wikipedia a heslo Thermophoresis.

Darcyho zákon (proudění podzemní vody)

V letech 1855 a 1856 francouzský inženýr H. Darcy pokusy prokázal přímou úměru mezi rozdílem tlaků na koncích trubice naplněné porézní zeminou (jednalo se vlastně o rozdíl výšek pro šikmou trubici) a rychlostí proudění vody touto trubicí. Pro tok podzemní vody je vhodné rozdíl tlaků vyjadřovat pomocí veličiny nazývané piezometrická výška \(h\). Do této veličiny se sčítá vliv nadmořské výšky, tlaku geologických vrstev a případné další efekty. Tok (množství vody, která proteče jednotkovou plochou za jednotku času) je dán vztahem \[\vec q=-K\nabla h,\] kde \(h\) je piezometrická výška a \(K\) je koeficient filtrace. Veličina \(K\) je v obecném případě symetrický tenzor. V izotropním případě má tok \(\vec q\) opačný směr než gradient veličiny \(h\) a v takovém případě se \(K\) redukuje na skalární hodnotu.

Ohmův zákon

Ohmův zákon je velice známý vztah mezi napětím a proudem. Přeformulováno z integrálního tvaru \(I=\frac 1R U\) (pro elektrické obvody) do diferenciálního tvaru (pro popis děje v látce) tento zákon říká, že hustota elektrického proudu \(\vec j\) je dána intenzitou elektrického pole \(\vec E\). A tato intenzita je gradientem potenciálu \(\varphi\) elektrického pole, tj. \(\vec E=\nabla \varphi\). Spojením těchto poznatků a při použití lineární aproximace dostáváme \[\vec j=-\gamma \nabla \varphi,\] což je Ohmův zákon v diferenciálním tvaru. Formálně máme tedy stejný tvar zákona jako u vedení tepla, tok tepla je nahrazen tokem elektrického proudu a rozdíl teplot je nahrazen rozdílem potenciálů. Znalost zapojování elektrických obvodů, jako je například paralelní nebo sériové zapojení rezistorů, bývá běžná a toho se často využívá při modelování tepelného odporu pomocí elektrického odporu. Formálně jsou vztahy identické.

Elektrický proud studujeme v kovech a ty bývají izotropní. Proto je v případě Ohmova zákona konstanta úměrnosti uvažována jako reálné číslo, nikoliv matice. Tím se věci znatelně zjednodušují, ale vyplývají odsud i limity použitelnosti při modelování vedení tepla jako vedení elektrického proudu. Například při průchodu elektrického proudu dřevem je konstanta úměrnosti z Ohmova zákona tenzorová a její nahrazení jedinou skalární hodnotou je pouze zjednodušení reálné situace.