Anotace.

• Ukážeme si důležitost znalosti směrů, jejichž obraz při maticovém zobrazení má stejný směr jako vzor.
• naučíme se hledat souřadné soustavy, ve kterých mají fyzikální vlastnosti vyjádřené pomocí matic nejjednodušší vyjádření.

Prerekvizity.

• Maticový součin
• Inverzní matice
• Soustavy rovnic
• Determinanty

Motivace. Dřevo má tři výrazné směry a pokud máme možnost zvolit souřadnou soustavu tak, aby tyto směry byly dány vektory \((1,0,0)^T\), \((0,1,0)^T\) a \((0,0,1)^T\), formulace fyzikálních zákonů se zjednoduší. Nyní si ukážeme proč. Najděte

1. nejobecnější matici \(3\times 3\), která zachovává směr vektoru \((1,0,0)^T\),
2. nejobecnější symetrickou matici \(3\times 3\), která zachovává směr vektoru \((1,0,0)^T\),
3. nejobecnější symetrickou matici \(3\times 3\), která zachovává směr vektorů \((1,0,0)^T\), \((0,1,0)^T\), \((0,0,1)^T\).

V tomto příkladě uvidíme, že matice zachovávající směr os souřadnic jsou v určitém smyslu pěkné.

Vlastní číslo (hodnota) a vlastní vektor (směr) matice

Vlastní čísla a vlastní vektory matice, pojmy představované v této přednášce, úzce souvisí se zobrazením vektorů pomocí matic a s tím, jestli mají vzor a obraz stejný směr. To poté, jak jsme viděli v úvodním příkladě, rozhoduje o tom, jak by měla vypadat souřadná soustava, ve které má matice diagonální vyjádření. Diagonální vyjáření je nejjednodušší možné, které dokáže zachytit anizotropní chování. Současně, jak uvidíme později, jsou diagonální matice dostatečně bohaté, abychom se na ně mohli omezit. Ukážeme si totiž, že pro každé zobrazení reprezentované symetrickou maticí se dá zvolit souřadná soustava tak, že v této soustavě má uvažované zobrazení diagonální matici.

Obecně se směr vektoru a směr jeho obrazu získaného jako součin matice s vektorem nemusí shodovat. Pokud se však shodují, je to do jisté míry pěkná situace. Pokud matice reprezentuje odezvu na podnět, znamená to, že odezva míří ve směru podnětu. To je něco, na co jsme zvyklí u izotropních materiálů, tj. u materiálů, které mají ve všech směrech stejné vlastnosti. U těch ostatních to znamená, že daný směr je v něčem speciální. U zobrazování vektorů pomocí maticového násobení nás velice zajímá, které směry se zachovávají, tj. kdy bude obrazem vektoru jeho násobek.

Definice (vlastní vektor a vlastní hodnota matice).

Řekneme, že nenulový vektor \(\vec u\) je vlastním vektorem matice \(A\) příslušným vlastní hodnotě \(\lambda\), jestliže platí \[A \vec u=\lambda \vec u.\]

Vlastní čísla se nazývají též vlastní hodnoty matice. Každý nenulový vlastní násobek vlastního vektoru je vlastní vektor příslušný téže vlastní hodnotě.

Poznámka (vlastní vektory a materiálové inženýrství).

Vlastní vektory jsou nesmírně důležité, protože definují směry, podél nichž se zobrazení chová “pěkně”. Tímto zobrazením může být třeba to, jak se působení vnější síly na těleso projeví na deformaci tohoto tělesa nebo jak se gradient teploty nebo vlhkosti projeví na proudění tepla či vody ve dřevě, půdě nebo jiném materiálu. Často se v aplikacích maticové zobrazení objevuje v konstitučních vztazích, vztazích mezi podnětem a materiálovou odezvou. Vlastní směry jsou tedy směry, ve kterých má odezva stejný směr jako podnět.

Pro pravidelně rostlé dřevo je snadné tyto směry určit, jsou to anatomické směry dřeva. Pro zkroucené dřevo nebo při studiu proudění vody, vzduchu či ropy v půdě to již tak snadné není a je nutné tyto směry vypočítat. To se naučíme později.

Příklad. Matice rotace nemá žádnou vlastní hodnotu (pokud tedy uvažujeme vlastní hodnoty v množině reálných čísel), protože pootočením se změní směr všech vektorů. Vlastní hodnoty existují pouze pro otočení o násobky \(180^\circ\).

Příklad. Matice \(\begin{pmatrix} 3 & 0\\ 0 & 3 \end{pmatrix}\) (trojnásobek jednotkové matice) zobrazuje každý vektor na trojnásobek a všechny vektory jsou vlastními vektory této matice. Příslušná vlastní hodnota je \(3\).

Příklad. Matice \(\begin{pmatrix} 3 & 0\\ 0 & 0 \end{pmatrix}\) má vlastní vektor \((1,0)\) příslušný vlastní hodnotě \(3\) a vlastní vektor \((0,1)\) příslušný vlastní hodnotě \(0\). Protože vlastními vektory jsou i nenulové násobky, je vlastním vektorem každý nenulový vektor, který má nulovou druhou komponentu (vlastní hodnota je \(3\)) nebo první komponentu (vlastní hodnota je \(0\)).

Příklad. Platí \(\begin{pmatrix} 3 & -2\\ -1 & 4 \end{pmatrix} \begin{pmatrix} 2\\1 \end{pmatrix} = \begin{pmatrix} 4\\2 \end{pmatrix}\) a matice \(\begin{pmatrix} 3 & -2\\ -1 & 4 \end{pmatrix}\) má vlastní vektor \((2,1)\) příslušný vlastní hodnotě \(2\), protože vektor \((4,2)\) je dvojnásobkem vektoru \((2,1)\). Vlastním vektorem je i každý nenulový násobek vektoru \((2,1)\).

Příklad. Vlastní hodnoty a vektory jsou jedním z hlavních stavebních kamenů algoritmu, kterým Google provádí hodnocení důležitosti webových stránek.

Transformace symetrické matice na diagonální tvar

Častým úkolem je zapsat vztahy mezi veličinami tak, aby byly co nejjednodušší a proto jeden z častých úkolů v lineární algebře bývá takovou šikovnou bázi nalézt.

Připoměňme si několik faktů, které je možno ověřit přímým rozepsáním.

• Je-li sloupcový vektor \(\vec e_1=(1,0,0)^T\) jednotkovým vektorem ve směru první z os a jedná se vlastní vektor s vlastní hodnotou \(\lambda_1\), potom se transformuje na sloupcový vektor \(\lambda_1 \vec e_1 = (\lambda_1,0,0)^T.\)
• Současně je \(A\vec e_1\) sloupcovým vektorem tvořícím první sloupec matice \(A\), ja jsme viděli v úvodním motivačním příkladě.
• Z předchozích dvou bodů vyplývá, že v souřadné soustavě, ve které je prvním bázovým vektorem vektor \(e_1\) má matice nenulový jenom prvek v hlavní diagonále a tento prvek je vlastní hodnotou.
• Opakováním předchozího pro další bázové vektory a další sloupce matice \(A\) vidíme, že jsou-li bázové vektory (vektory ve směrech os) vlastními vektory, je matice zobrazení v této bázi diagonální a v této diagonále jsou vlastní čísla matice.
• Pokud vlastní vektory nejsou ve směrech os, ale mají libovolné souřadnice, potom matice \(P\) tvořená po sloupcích souřadnicemi těchto vektorů se nazývá matice přechodu

Je otázkou, jestli vlastních hodnot a vlastních vektorů je tolik, kolik pro plnou diagonalizaci “potřebujeme”. Částečně pozitivní odpověď na tuto otázku udávají věty na následujícím slidu.

Věta (vlastní čísla symetrické matice).

Symetrická čtvercová matice \(A\) řádu \(n\) má \(n\) reálných vlastních čísel (počítáno i s případnou násobností).

Věta (diagonalizace symetrické matice).

Nechť má symetrická čtvercová matice \(A\) řádu \(n\) celkem \(n\) reálných různých vlastních čísel \(\lambda_i\). Označme odpovídající vlastní vektory jednotkové délky \(\vec v_i\).

• Matice \(P\) sestavená tak, že sloupce této matice jsou tvořeny vektory \(\vec v_i\) je ortogonální.
• Matice \(D\) definovaná vztahem \[D=P^TAP\] je diagonální.
• Diagonální prvky matice \(D\) jsou právě vlastní čísla \(\lambda_i\) a jsou ve stejném pořadí jako odpovídající vlastní vektory v matici \(P\).

Poznámka (diagonální tvar materiálových vlastností dřeva).

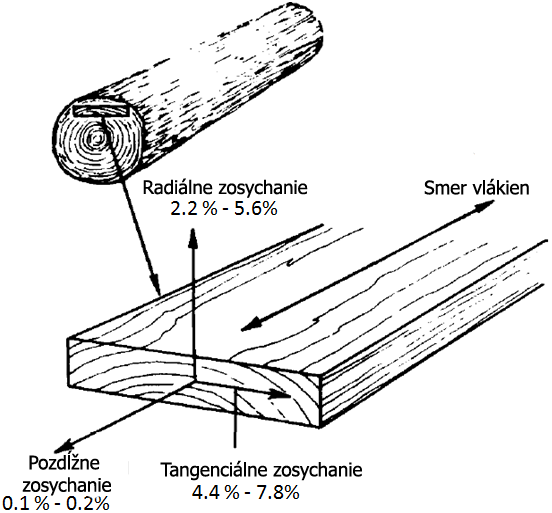
Typickým ortotropním materiálem je dřevo. Pokud transformujeme tenzor difuzní matice pro dřevo na diagonální tvar, jsou diagonální prvky v poměru přibližně \(D_L:D_R:D_T=35:3:2\) (P. Horáček, Fyzikální a mechanické vlastnosti dřeva, 2008 , str. 65). Ortotropní charakter má však nejenom transport tekutin, ale i sesychání a bobtnání. V tomto případě však naopak v podélném směru dřevo bobtná nejméně a tenzor popisující bobtnání má po transformaci na diagonální tvar v diagonále prvky v poměru přibližně \(\alpha_T:\alpha_R:\alpha_L=20:10:1\) (P. Horáček, Fyzikální a mechanické vlastnosti dřeva, 2008 , str. 38).

Matice transformace \(P\) z předchozí věty je ortogonální (její transponovaná matice je současně její inverzní matice) a její determinant (veličina, se kterou se seznámíme vzápětí) je roven \(1\) nebo \(-1\). Pokud je determinant kladný, reprezentuje matice pootočení soustavy souřadnic. Pokud je determinant záporný, jedná se o pootočení spojené se zrcadlením jedné osy. Protože tento případ většinou z fyzikálních důvodů nepreferujeme, sestavujeme matici transformace tak, aby měla determinant kladný. V případě záporného determinantu stačí prohodit dva vektory (sloupce matice transformace) mezi sebou, nebo jeden vynásobit faktorem \(-1\).

Pro kontrolu je zajímavé vědět, že determinant matice se pootočením nemění a je tedy stejný pro původní i transformovanou matici. Totéž platí pro součet prvků v hlavní diagonále (v lineární algebře se nazývá stopa matice), pro charakteristický polynom a pro vlastní hodnoty. Tenzor, jak jej uvažujeme v tomto textu, je matice, která má navíc fyzikální význam a vzhledem ke své povaze pro ni platí speciální transformační pravidla. Nicméně je to mimo jiné i matice a proto vše výše uvedené platí i pro tenzory.

Transformace tenzorů je užitečná a důležitá činnosti. Bohužel však vzorce s touto transformací spojené nejsou natolik zapamatovatelné, aby bylo obvyklé s nimi pracovat. Možnosti jsou v zásadě tři.

• Mít vzorce v psané podobě po ruce a pouze do nich dosazovat.
• Mít k dispozici jednoduše zapamatovatelný postup, jak s transformacemi pracovat. Takový postup existuje, nazývá se Mohrova kružnice a po zapracování se jedná o efektivní grafickou metodu pro transforamci tenzorů. Zpravidla je v literatuře popsána pro tenzor napětí, funguje však obecně.
• Pracovat pouze s elementárními prostředky lineární algebry. Narozdíl od předchozích bodů máme přehled o tom, co a proč děláme (oproti vzorcům) a nemusíme se učit další metodu (oproti Mohrově kružnici).

Determinant matice

Pojmy lineární algebry spolu krásně souvisí.

Věta.

Buď \(A\) čtvercová matice řádu \(n\). Následující výroky jsou ekvivalentní:

1. K matici \(A\) existuje matice inverzní \(A^{-1}\).
2. Matice \(A\) je regulární, tj. \(\det A\neq 0\).
3. Soustava lineárních rovnic \[AX=B\] má pro libovolnou pravou stranu \(B\) jediné řešení.
4. Homogenní soustava lineárních rovnic \[AX=0\] má pouze nulové řešení.
5. Každý vektor z \(\mathbb R^n\) lze vyjádřit jako lineární kombinaci vektorů tvořených řádky (sloupci) matice \(A\), a to jednoznačně, až na pořadí.

Například je-li \(\vec q\) vlastním vektorem matice \(A\) příslušným vlastní hodnotě \(\lambda\), platí \[A\vec q=\lambda \vec q.\] Odsud \[\begin{aligned}A\vec q-\lambda \vec q&=0\\ A\vec q-(\lambda I )\vec q &=0\\ (A-\lambda I )\vec q &=0\end{aligned}.\] Pokud chápeme poslední rovnost jako soustavu rovnic s koeficienty \((A-\lambda I)\), nulovou pravou stranou a nenulovým řešením \(\vec q\) (tj. bod 4 předchozí věty neplatí), musí být determinant matice \(A-\lambda I\) nulový (tj. bod 2 předchozí věty neplatí). Tím je motivována následující definice a dokázána následující věta.

Definice (charakteristická rovnice, charakteristický polynom).

Rovnice \[\det (A-\lambda I)=0\] s neznámou \(\lambda\) se nazývá charakteristická rovnice matice \(A\). Výraz na levé straně této rovnice je polynom proměnné \(\lambda\) a nazývá se charakteristický polynom matice \(A\).

Důsledek (vlastní čísla).

Vlastní čísla matice \(A\) jsou právě řešení charakteristické rovnice. Vlastní vektor \(\vec u\) příslušný vlastnímu číslu \(\lambda\) je nenulové řešení homogenní soustavy rovnic \[(A-\lambda I)\vec u=0.\]

Příklad transformace matice na diagonální tvar

Ukážeme si postup na jednoduchém příkladě. Pro srovnání je možno postup založený na dosazování do vzorců shlédnout na https://www.youtube.com/watch?v=xdxVpC856ms. V průběhu počítání vyřešíme soustavu dvou rovnic o dvou neznámých. To je úloha známá ze střední školy. Jak opostupovat v komplikovanějších případech, kdy je rovnic více, si ukážeme v další přednášce. V té se budeme zabívat libovolně velkými soustavami rovnic.

Příklad. Odvodíme diagonální tvar tenzoru napětí \[A= \begin{pmatrix} 20 & 30 \\ 30 & -10 \end{pmatrix}. \] Tím najdeme maximální hodnotu normálového napětí a směr, ve kterém působí. Charakteristický polynom této matice je \[\det(A-\lambda I)= \begin{vmatrix} 20-\lambda & 30 \\ 30 & -10-\lambda \end{vmatrix}= (20-\lambda)(-10-\lambda)-30^2=\lambda^2-10\lambda-1100 \] s kořeny \(\lambda_1\approx 38.54\) a \(\lambda_2\approx -28.54\). To budou prvky v hlavní diagonále po transformaci tenzoru.

Pokud budeme chtít vědět, jak jsou nové osy orientovány vůči osám původním, musíme najít i vlastní vektory. Vlastní vektor příslušný hodnotě \(\lambda_1\) je řešením soustavy s maticí soustavy \[ A-\lambda_1 I\approx \begin{pmatrix} -18.54 & 30 \\ 30 & -48.54 \end{pmatrix} \] a nulami vpravo. Přibližným řešením je vektor \(\vec u_1= \begin{pmatrix} 30 \\ 18.54 \end{pmatrix}\). (Toto plyne z první rovnice, druhá rovnice musí být splněna automaticky, protože jsme použili vlastní hodnotu a soustava musí mít nenulové řešení. Nicméně výpočet je zatížen zaokrouhlovací chybou.) Po vydělení normou vektoru dostáváme \(\begin{pmatrix} 0.851 \\ 0.526 \end{pmatrix}\). Druhý vlastní vektor je kolmý, tj. \(\begin{pmatrix} -0.526 \\ 0.851 \end{pmatrix}\). Po transformaci maticí \(P= \begin{pmatrix} 0.851 & -0.526 \\ 0.526 & 0.851 \end{pmatrix}\) dostáváme (na dvě desetiná místa) \[P^{T}\begin{pmatrix} 20 & 30 \\ 30 & -10 \end{pmatrix} P=\begin{pmatrix} 38.54 & 0 \\ 0 & -28.54 \end{pmatrix}. \] To vlastně ani nemusíme počítat, věta v úvodu tohoto slidu zaručuje, že výsledná matice bude diagonální a bude obsahovat vlastní hodnoty. Z matice \(P\) vidíme sinus a kosinus úhlu pootočení a odsud určíme snadno, o kolik se souřadná soustava otáčí a v jakém směru.