Anotace.

• Seznámíme se s popisem transformace bodů, vektorů a tenzorů do jiných souřadnic.
• Seznámíme se s možnostmi lineární aproximace od skalárních funkcí po vektorové funce více proměnných. Využití je například při popisu deformace tělesa.

Prerekvizity.

• Maticový součin
• Lineární aproximace funkce jedné proměnné

Matice

Matice jako zobrazení v geometrii

• Součin matice a vektoru je lineární kombinace sloupců matice s koeficienty podle komponent vektoru. \[ \begin{pmatrix} a & b\\c&d\end{pmatrix} \begin{pmatrix} x_1 \\x_2\end{pmatrix} = x_1\begin{pmatrix} a \\c\end{pmatrix} + x_2\begin{pmatrix} b \\d\end{pmatrix} \]
• Součin dvou matic je matice, jejíž sloupce dostaneme jako součiny první matice s vektory tvořenými sloupci druhé matice.
• Jsou-li vektory v součinu jednotkovými vektory ve směru os, jsou výsledkem maticového součinu přímo sloupce matice. To plyne přímým výpočtem. \[\begin{pmatrix} a & b\\c&d\end{pmatrix} \begin{pmatrix} 1 \\0\end{pmatrix} = \begin{pmatrix} a \\c\end{pmatrix} \] \[\begin{pmatrix} a & b\\c&d\end{pmatrix} \begin{pmatrix} 0 \\1\end{pmatrix} = \begin{pmatrix} b \\d\end{pmatrix} \]
• Je-li \(f\) zobrazení vektorů na vektory, které zachovává součet a násobek, je možné toto zobrazení vyjádřit ve tvaru \(f(X)=AX\) pro vhodnou matici \(A\). Vzhledem k předchozímu je matice a tím i zobrazení jednoznačně určeno obrazy jednotkových vektorů ve směrech os. Tedy informace o celém zobrazení je skryta ve dvou malých snadno dostupných informacích, obrazech jednotkových vektorů ve směru os.
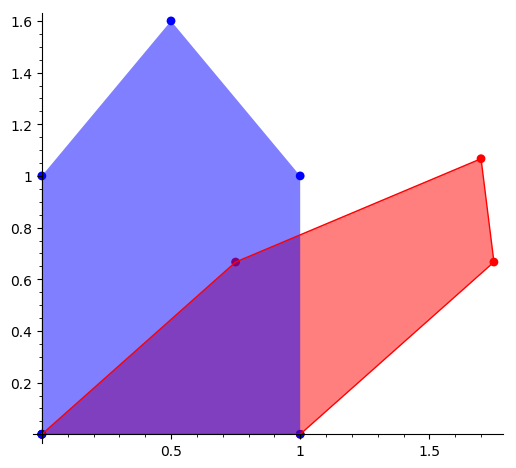
• Uvažujeme-li v předchozím místo vektorů body roviny nebo prostoru, dostaneme pomocí maticového násobení všechny transformace roviny nebo prostoru, které zachovávají rovnoběžnost a dělící poměry úseček (například středy úseček). Ukázka zobrazení ve 2D.

Matice rotace

Matice \[R_\theta= \begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix} \] zobrazí vektory \(e_1=(1,0)\) a \(e_2=(0,1)\) na \[\begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} 1\\0 \end{pmatrix} = \begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix} \] a \[\begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} 0\\1 \end{pmatrix} = \begin{pmatrix} -\sin\theta \\ \cos\theta \end{pmatrix}. \] Proto matice \(R_\theta\) definuje zobrazení, které pootočí rovinu o úhel \(\theta\) a nazývá se matice rotace.

Matice jako zobrazení v materiálovém inženýrství

Matice chápejme jako zobrazení, které má na vstupu vektor a na výstupu opět vektor. Vstupem bývá většinou podnět, kde rozhodující je nejenom síla podnětu, ale i jeho směr. Například nerovnováha tlaku. Výstupem bývá odezva, například proudění vyvolané nerovnováhou tlaku. Tato odezva v izotropním prostředí má směr podnětu, v prostředí s určitou strukturou by se však směr odezvy mohl odchýlit.

Užitečnost maticového součinu v materiálovém inženýrství si můžeme znázornit na proudění vody po povrchu země. Voda teče z kopce dolů, tento směr však můžeme ovlivnit vyoráním brázd. Hnací síla je gravitace, která směřuje z kopce dolů. Odezvou na gravitaci je tok vody, který směřuje velkou rychlostí dolů, pokud je pooráno po spádnici, malou rychlostí dolů, pokud je pooráno po vrstevnici a pokud je pooráno našikmo, tak něco mezi směrem dolů a směrem brázdy. V materiálu se může odehrávat totéž.

Výše popsané chování pozorujeme i u proudění podzemní vody, kde hnací silou kromě hladiny podzemní vody může být tlak, nebo u proudění vody ve dřevě, kde hnací silou definující pojem “z kopce dolů” je nerovnoměrnost v rozložení koncentrace vody ve dřevě (jedna část dřeva má větší vlhkost než jiná část) nebo nerovnoměrnost v teplotě (termodifuze, Sorettův efekt, transport vlhkosti vyvolaný rozdílem teplot). Výsledné proudění však nemusí přesně sledovat pokles koncentrace vlhkosti. Například dřevo vede podélně vlhkost zpravidla více než desetkrát lépe než v jiných směrech a chová se tedy, jako by v něm byly brázdy odklánějící vodu do podélného směru.

Matematický prostředek, který umožňuje snadno vektoru změnit velikost nebo i směr je právě matice a maticový součin.

Transformace souřadnic vektoru

Uvažujme souřadnou soustavu \(B\) a souřadnou soustavu \(B'\), která vznikne z \(B\) pootočením o úhel \(\theta\). Tedy bázové vektory soustavy \(B'\) vzniknou součinem matice rotace \(R\) a bázových vektorů soustavy \(B\). Uvažujme libovolný vektor a jeho souřadnice v soustavách \(B\) a \(B'\) označme \(X\) a \(X'\). Zobecněním postupu z prezentace o maticích (viz též obrázek) dostáváme \[X=RX'\]

Transformace souřadnic tenzoru

Označme \(X\), \(Y\) a \(A\) postupně obraz, vzor a matici zobrazení v nějaké souřadné soustavě \(B\). Tedy \[Y=AX.\] Označme čárkovaně vzor a obraz v otočené soustavě \(B'\), kde matice přechodu je \(R\). Tedy \(X=RX'\) a \(Y=RY'\), kde sloupce matice \(R\) jsou jednotkové vektory báze \(B'\). Z výše uvedených vztahů dostáváme \[RY' = A RX'\] a vynásobením zleva maticí inverzní \(R^{-1}\) dostáváme \[Y' = R^{-1}A R X'.\] To znamená, že matice \[R^{-1}AR\] je matice převádějící \(X'\) na \(Y'\) a jedná se tedy o matici zobrazení v soustavě \(B'\).

Postup funguje pro libovolnou transformaci \(R\), nejenom rotaci. Ale protože rotace je prakticky nejzajímavější, dodejme, že v takovém případě je inverzní matice rovna matici transponované a určíme ji tedy velmi snadno.

Lineární aproximace

V následujících pasážích se budeme věnovat lineární aproximaci funkce. To je nahrazení funkce s jakkoli složitým funkčním předpisem funkcí s tím nejjednodušším možným předpisem: lineární funkcí. Tím se pochopitelně dopouštíme jisté nepřesnosti a je to něco za něco: k popisu úlohy máme poté k dispozici jednodušší funkce, ale výpočty jsou zatíženy chybou. Někdy tato chyba může být tak velká, že je idea lineární aproximace naprosto nepoužitelná. Ale jindy se jedná o nástroj, který prakticky neřešitelnou úlohu převede na úlohu snadno zvládnutelnou. Linearizace nelineárních úloh je jedním ze základních inženýrských postupů. V mnoha případech dává samotná dobré výsledky a řeší zadaný problém, v jiných případech slouží jako odrazový můstek ke zvládnutí nelineárního problému.

Lineární aproximace jak je používáme v běžném životě

Příklad (růst stromu). Strom má v roce 2019 výšku 3 metry a roste rychlostí 0.5 metru za rok. V roce \(x\) je jeho výška dána vzorcem \[h(x)=3+0.5(x-2019).\]

Lineární aproximace v 1D

Pokud se funkce mění, můžeme odhad změny přičíst k funkční hodnotě a tím máme odhad funkční hodnoty po změně. Toto je principem lineární aproximace, neuvěřitelně jednoduché a přitom velice mocné techniky používané inženýry k tomu, aby se popis problémů a řešení úloh vůbec daly efektivně zvládnout.

Věta (lineární aproximace).

Buď \(f:\mathbb R\to\mathbb R\) funkce, která má derivaci. V okolí bodu \(x_0\) platí přibližný vzorec \[f(x)\approx f(x_0)+ f'(x_0)(x-x_0)\] neboli \[f(x)\approx f(x_0)+ \frac{\mathrm df(x_0)}{\mathrm dx}(x-x_0).\]

Poznámka (slovní interpretace vzorce pro lineární aproximaci).

Výše uvedený vzorec není těžké rozšifrovat.

• Veličina \(f(x)\) je funkční hodnota v bodě \(x\), tu chceme odhadnout.
• Veličina \(f(x_0)\) je známá funkční hodnota v bodě \(x_0\), to je výchozí bod pro odhad.
• Veličina \(f'(x_0)\) je odhad změny veličiny \(f\) způsobený jednotkovou změnou vstupních dat (zvýšení hodnoty \(x_0\) o jednotku). Tento faktor ještě v dalším kroku musíme přizpůsobit tomu, že změna vstupních dat není jednotková, což uděláme s využitím přímé úměrnosti.
• Veličina \(f'(x_0)(x-x_0)\) je odhad změny veličiny \(f\) vyvolané změnou veličiny \(x\) z \(x_0\) o \(\Delta x=x-x_0\) tak, jak jsme jej používali v minulé přednášce.

Poznámka (alternativní vzorec pro lineární aproximaci).

Vzorec pro lineární aproximaci se často píše v ekvivalentním tvaru \[f(x+h)\approx f(x)+f'(x)h,\] což získáme dosazením \(x+h\) za \(x\) a \(x\) za \(x_0\).

Příklad (aproximace důležitých funkcí v okolí nuly). Přímým použitím uvedeného vzorce je možno ukázat platnost následujících přibližných vzorců, které platí pro \(x\) blízké k nule. \[\sin x\approx x, \quad \cos x\approx 1,\qquad (1+x)^n\approx 1+nx.\] První dva vzorce využijeme později při popisu malých rotací v rovině. Mnoho důležitých aplikací těchto vzorců ve fyzice je na webu fyzikální olympiády v dokumentu Aproximace ve fyzikálních úlohách.

Příklad (matice malých rotací). Matice malých rotací je (použitím lineární aproximace \(\sin\theta\approx \theta\) a \(\cos \theta\approx 1\) v okolí nuly) \[R_{\theta,0}= \begin{pmatrix} 1 & - \theta\\ \theta & 1 \end{pmatrix}. \] Tuto matici budeme potřebovat při studiu deformace při odvození matematického popisu malých deformací.

Lineární aproximace skalární funkce více proměnných

Lineární aproximaci funkce \(z=f(x,y)\) v bodě \((x_0, y_0)\) napíšeme analogicky jako pro jednu proměnnou, ale uplatní se změna v každé z proměnných. Tedy \[ f(x,y)\approx f(x_0, y_0)+\frac{\partial f (x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial f (x_0,y_0)}{\partial y}(y-y_0)\] nebo (pomocí skalárního součinu) \[ f(x,y)\approx f(x_0, y_0)+ \left(\frac{\partial f (x_0,y_0)}{\partial x},\frac{\partial f (x_0,y_0)}{\partial y}\right)\cdot (x-x_0,y-y_0).\]

Lineární aproximace vektorové funkce

Lineární aproximací vektorové funkce je lineární aproximace jejích skalárních složek. Tj. pro funkci \(\vec F(x,y)=f_1(x,y)\vec \imath + f_2(x,y)\vec\jmath\) v bodě \((x_0, y_0)\) je \[ f_1(x,y)\approx f_1(x_0, y_0)+\frac{\partial f_1 (x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial f_1 (x_0,y_0)}{\partial y}(y-y_0)\] a \[ f_2(x,y)\approx f_2(x_0, y_0)+\frac{\partial f_2 (x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial f_2 (x_0,y_0)}{\partial y}(y-y_0).\] Vektorově zapsáno, platí \[\begin{pmatrix}f_1(x,y)\\f_2(x,y)\end{pmatrix} \approx \begin{pmatrix}f_1(x_0,y_0)\\f_2(x_0,y_0)\end{pmatrix} + \begin{pmatrix} \frac{\partial f_1}{\partial x}(x_0,y_0) \\\frac{\partial f_2}{\partial x}(x_0,y_0) \end{pmatrix} (x-x_0)+ \begin{pmatrix} \frac{\partial f_1}{\partial y}(x_0,y_0)\\ \frac{\partial f_2}{\partial y}(x_0,y_0)\end{pmatrix} (y-y_0). \] Maticově zapsáno \[\begin{pmatrix}f_1(x,y)\\f_2(x,y)\end{pmatrix} \approx \begin{pmatrix}f_1(x_0,y_0)\\f_2(x_0,y_0)\end{pmatrix} + \begin{pmatrix} \frac{\partial f_1}{\partial x}(x_0,y_0) & \frac{\partial f_1}{\partial y}(x_0,y_0)\\\frac{\partial f_2}{\partial x}(x_0,y_0) & \frac{\partial f_2}{\partial y}(x_0,y_0)\end{pmatrix} \begin{pmatrix}x-x_0\\ y-y_0\end{pmatrix} \] nebo \[\vec F(x,y)\approx \vec F(x_0,y_0) + J(x_0,y_0) \begin{pmatrix}x-x_0\\ y-y_0\end{pmatrix},\] kde \[J(x,y)=\begin{pmatrix} \frac{\partial f_1}{\partial x}(x ,y ) & \frac{\partial f_1}{\partial y}(x ,y )\\\frac{\partial f_2}{\partial x}(x ,y ) & \frac{\partial f_2}{\partial y}(x ,y )\end{pmatrix}\] je Jacobiho matice funkce \(\vec F\).

Lineární aproximace v okolí nuly pro funkci, která je v nule nulová, tj. \(x_0=y_0=\vec F(0,0)=0\) je \[\vec F(x,y)\approx J(0,0) \begin{pmatrix}x\\ y\end{pmatrix}.\]

Tenzor malých deformací

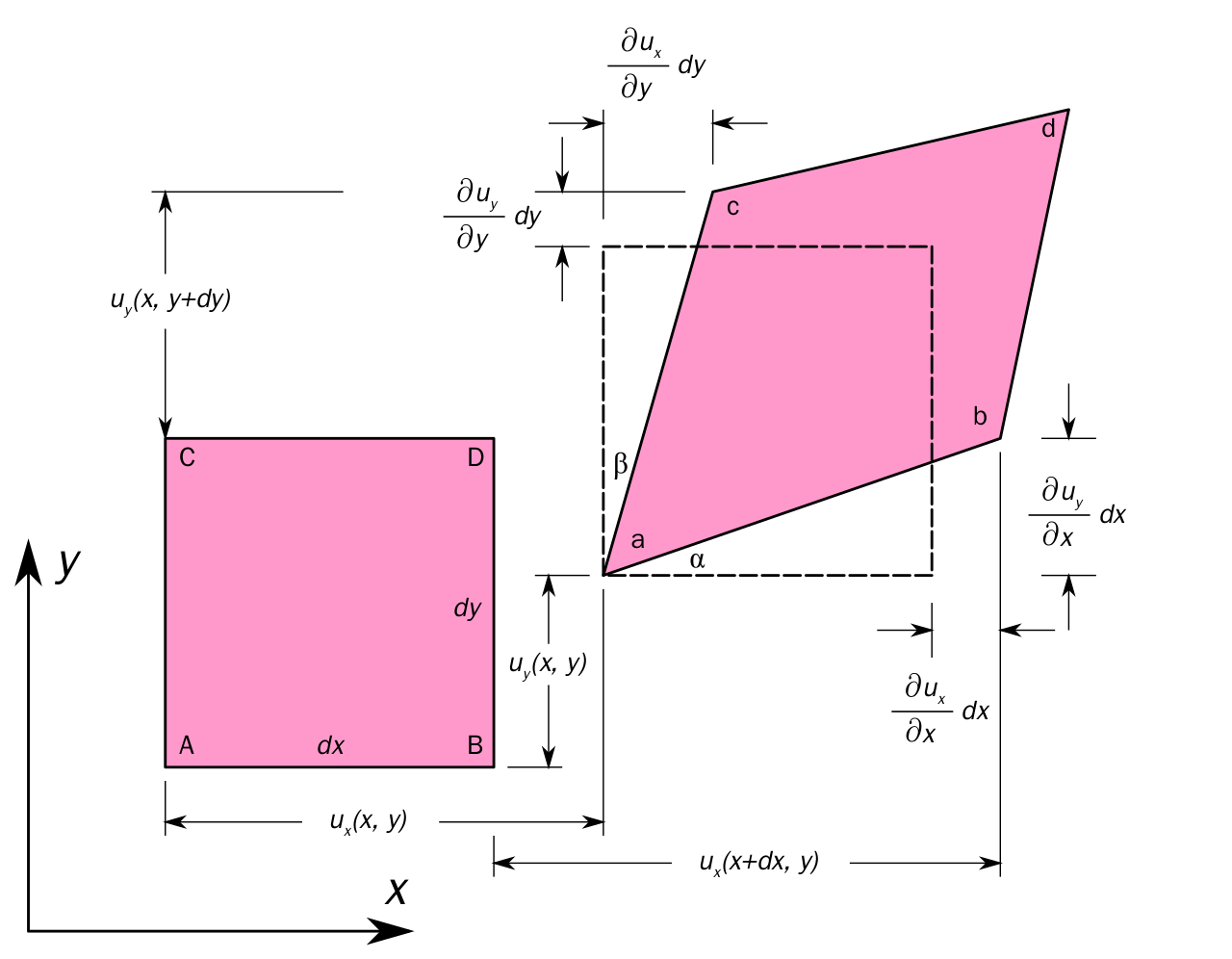
Ukážeme si, že parciální derivace a maticový počet jsou vhodné k popisu deformací.

Vektorovou funkci je možné chápat jako zobrazení roviny do sebe, které může odpovídat transformaci tělesa, například působením síly. Popišme tuto deformaci vektorem \(\vec U(x_1,x_2)=(u_1(x_1,x_2), u_2(x_1,x_2))\). Udává o kolik a kterým směrem se posune bod o souřadnicích \((x_1,x_2)\). Pokud je tato vektorová funkce nulová, s tělesem se nic neděje, zůstává na místě. Pokud je konstantní, každý bod se posune stejně a jedná se o posun bez změny tvaru. V obecném případě však tato funkce konstantní není. Lineární aproximací v bodě \((x_1,x_2)\) dostáváme \[\vec U(x_1+\Delta x_1,x_2+\Delta x_2)\approx \vec U(x_1,x_2) + J(x_1,x_2) \begin{pmatrix}\Delta x_1 \\ \Delta x_2 \end{pmatrix}.\] Člen \(\vec U(x_1,x_2)\) je posunutí, proto nás zajímá až druhý člen, obsahující deformaci. Pokud matici \(J(x_1,x_2)\) rozdělíme na součet symetrické a antisymetrické matice, dostaneme matici, odpovídající změně tvaru a matici, odpovídající pootočení. Pootočení (antisymetrická část) nás nezajímá, zajímá nás jenom změna tvaru. Obecný postup, jak rozdělit matici na součet symetrické a antisymetrické matice je \[A=\frac{A+A^T}2+\frac{A-A^T}2.\] První matice v tomto součtu je symetrická a druhá antisymetrická. Pro Jacobiho matici dostáváme \[\frac{J+J^T}2= \begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)\\ \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)& \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} .\] Tato matice popisuje změnu tvaru a nazývá se tenzor malých deformací. Ten se ještě někdy rozděluje na součet vhodného konstantního násobku jednotkové matice (souvisí se zvětšením nebo zmenšením, tj. se změnou objemu) a deviátor (souvisí se změnou tvaru bez započtení zvětšení či zmenšení).

Pro využití v dřevařských úlohách viz též A. Požgaj, Štruktúra a vlastnosti dreva str 318 nebo P. Horáček, Fyzikální a mechanické vlastnosti dřeva I, str. 40. Analogicky, ale pro rychlosti, je definován tenzor rychlosti přetvoření (deformační rychlost) používaný v hydrodynamice. Můžeme ji dostat jako derivaci tenzoru malých deformací (při studiu deformací), nebo jako symetrickou část matice vytvořené gradienty jednotlivých komponent rychlosti proudění. Pro proudění vody viz J. Říha, Matematické modelování hydrodynamických a disperzních jevů, kap. 3.3.

Obrázky a online výpočty.

Transformace tenzoru malých deformací

Popis deformací je neintuitivní v tom, že deformace rovinného objektu se popisuje pomocí tří veličin, deformace prostorového tělesa pomocí šesti veličin. Navíc závisí na souřadné soustavě, ve které deformaci popisujeme.