Anotace.

• Naučíme se sledovat rychlost, s jakou se mění veličina, která je objektem našeho zájmu.
• Budeme schopni sledovat rekci sledované veličiny na současné změny více parametrů. Například u teploty můžeme sledovat jak se v daném místě mění teplota v čase, nebo jak se v daný okamžik mění teplota s polohou.
• Aparát využijeme k tomu, že z fyzikálních zákonů sestavíme rovnici vedení tepla. To bude matematický model umožňující jednak modelování přenosu tepla a jednak kontrolu toho, že fyzikální zákony vedoucí k formulaci této rovnice jsou správné.

Prerekvizity.

• Navážeme na znalosti z diferenciálního počtu funkcí jedné proměnných. Zejména definice a využití derivace. Tyto partie si připomeneme.
• Zopakujte si fyzikální (praktický) význam derivace. Velmi pomůže, pokud pracujeme i s jednotkami veličin.

Rychlost růstu funkce jedné proměnné

Příklad (motivace, rychlost růstu funkce dané tabulkou)

Tabulka udává závislost teploty vzduchu venku na čase. Nejprve se ráno otepluje, v okolo poledne se začne ochlazovat.

Rychlost růstu vypočteme snadno (pomocí rozdílu), ale máme jenom hrubou informaci. Nevíme, co se dělo během jednotlivých hodin.

čas \(t\) v hod	teplota vzduchu \(T\) ve \(^\circ \mathrm{C}\)	rychlost růstu teploty vzduchu v následující hodině \(\Delta T/\Delta t\) ve \({}^\circ \mathrm C/\mathrm{hod}\)
8:00	12	6
9:00	18	2
10:00	20	0
11:00	20	−2
12:00	18

Příklad (motivace, rychlost růstu spojité funkce)

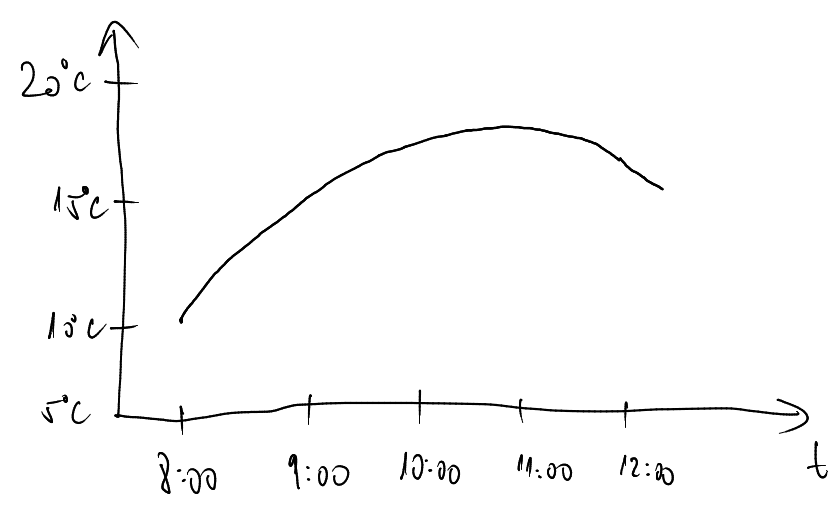
Graf udává závislost teploty vzduchu venku na čase. Nejprve se ráno otepluje, okolo poledne se začne ochlazovat, tedy stejná situace jako výše.

Rychlost růstu sice vypočteme komplikovaně (pomocí derivace), ale může se to vyplatit. Díky tomu totiž máme o procesu detailní informaci. Víme přesně jak se mění hodnota v každém okamžiku.

Derivace funkce jedné proměnné

Opakování, detaily

Buď \(y=f(x)\) funkce definovaná na nějakém otevřeném intervalu.

Definice (derivace).

Derivací funkce \(f\) v bodě \(x\) rozumíme limitu \[\frac{\mathrm df}{\mathrm dx}:=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}.\]

Derivaci funkce \(f\) v bodě \(x_0\) označujeme \(f'(x_0)\) nebo \(\frac{\mathrm df(x_0)}{\mathrm dx}\). Derivaci v libovolném bodě potom \(f'\), \(f'(x)\) nebo \(\frac{\mathrm df}{\mathrm dx}\). Zápis \(\frac{\mathrm df}{\mathrm dx}\) je Leibnizova notace, zápis \(f'\) je Lagrangeova notace.

Poznámka (slovní interpretace definice derivace).

• Výraz z čitatele, tj. \(f(x+h)-f(x)\), je změna veličiny \(f\) na intervalu \([x,x+h]\). Často označujeme též \(\Delta f\).
• Podíl, tj. \(\frac{f(x+h)-f(x)}h\) je změna veličiny \(f\) na intervalu \([x,x+h]\) přepočítaná na jednotku veličiny \(x\), tj. v jistém smyslu průměrná rychlost na tomto intervalu. Často označujeme též \(\frac{\Delta f}{\Delta x}\).
• Limita v definici derivace stahuje délku intervalu, na kterém počítáme průměrnou rychlost, k nule. Tím se z průměrné rychlosti stane okamžitá rychlost.

WW-otázka

Interpretace derivace v nematematických disciplínách je okamžitá rychlost s jakou veličina \(f\) reaguje na změny veličiny \(x\). Často studujeme veličiny závislé na čase s v tomto případě jde tedy o rychlost, s jakou se veličina mění v čase. Další možnosti a obraty používané pro slovní vyjádření derivace jsou zmíněny níže v podkapitole věnované derivaci podle času. Analogickou terminologii (rychlost růstu, rychlost změny) zpravidla přenášíme i na případy, kdy nezávislou proměnnou není čas. Rychlost potom chápeme v abstraktním slova smyslu.

Obecně, ať již je nezávislou proměnnou čas či jiná veličina, se derivace \(f'(x)\) často slovně interpretuje jako veličina, která udává, jak se mění veličina \(f\) při změnách veličiny \(x\). Tímto slovním obratem je myšlena změna veličiny \(f\), odpovídající změně veličiny \(x\) o jednotku. Je to podobné, jako údaj o rychlosti na tachometru v automobilu. Ten udává, kolik kilometrů ujedeme za hodinu. Od skutečně uražené dráhy se tento údaj může lišit, protože pohyb může trvat třeba jenom deset minut. A kdyby jízda opravdu trvala hodinu, mohlo vlivem jízdy v zácpě dojít k podstatnému nesouladu se skutečně uraženou dráhou. Přesto je okamžitá rychlost ukazovaná na tachometru při jízdě automobilem užitečná veličina a nemáme problémy s jejím chápáním. Stejně tak pohlížejme na derivaci.

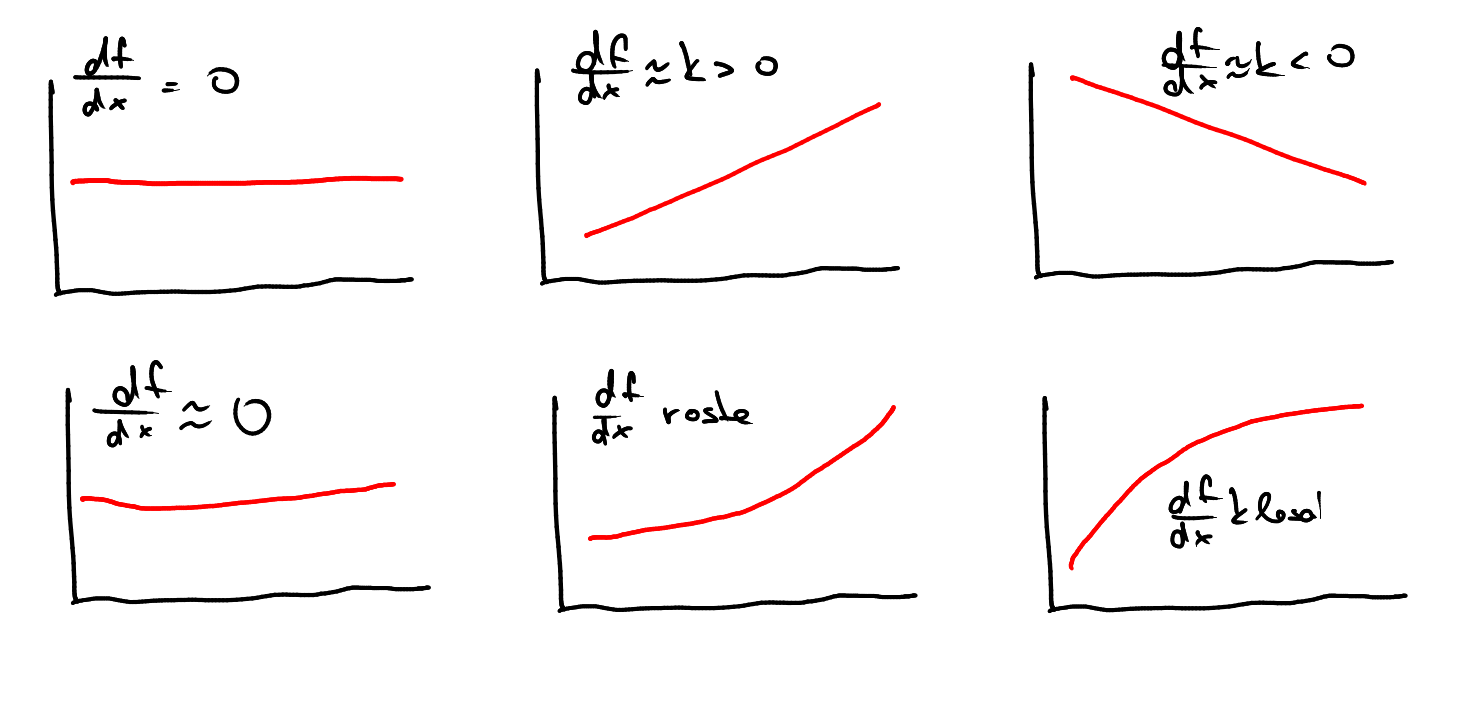
WW-otázka

Derivace funkce	Chování funkce
Derivace je nulová.	Funkce je konstantní. Sledovaná veličina se nemění při zmeně vstupních dat.
Derivace je kladná.	Funkce roste. Pokud data na vstupu rostou, sledovaná veličina také roste.
Derivace je záporná.	Funkce klesá. Pokud data na vstupu rostou, sledovaná veličina klesá.
Derivace je numericky malá (blízká k nule).	Funkce se mění pomalu. Sledovaná veličina reaguje na změny ve vstupních datech pouze málo.
Derivace je numericky velká (hodně kladná nebo hodně záporná).	Funkce se mění rychle. Malá změna na vstupu má velký vliv na sledovanou veličinu.
Derivace je konstantní.	Funkce je lineární. Klesá nebo roste pořád stejně rychle. Pokud vstup roste aritmetickou řadou (po stejných skocích), sledovaná veličina roste nebo klesá také aritmetickou řadou.
Derivace roste.	Funkce je nelineární a roste stále rychleji. Pokud je funkce kladná, rostoucí derivace znamená, že růst se stále zrychluje.
Derivace klesá k nule.	Funkce je nelineární a přibližuje se k vodorovné asymptotě. Pokud je funkce kladná, k nule klesající derivace znamená, že růst se stále zpomaluje a zastaví se.

Poznámka (jednotka derivace).

Jednotka derivace \(\frac{\mathrm df}{\mathrm dx}\) funkce \(f(x)\) je stejná, jako jednotka podílu \(\frac {f(x)}x\).

Aplikace derivací 1: Jak rychle? (změna v čase)

Poznámka (slovní vyjádření derivace podle času).

Derivace v bodě, pokud ji nahlížíme z hlediska časové změny veličiny, je okamžitá rychlost s jakou se mění tato veličina. Protože kladná změna je růst, nahrazujeme někdy slovo “změna” slovem “růst”. Protože rychlost je změna za jednotku času, nahrazujeme někdy slovo “rychlost” obratem “změna za jednotku času”. Derivaci podle času můžete tedy přečíst libovolným z následujících obratů. Všechny se běžně používají a všechny chápeme stejně – jako derivaci podle času.

• Rychlost růstu
• Rychlost změny (implicitně předpokládáme, že kladná změna odpovídá růstu a záporná změna poklesu)
• Nárůst za jednotku času
• Změna za jednotku času
• Časová změna veličiny

Pokud potřebujeme pracovat s poklesem, násobíme derivaci faktorem \(-1\). Toto čteme též jako “záporně vzatá derivace.”

Zákon ochlazování

Horké těleso o teplotě \(T\) je v chladnější místnosti o teplotě \(T_0\). Z fyziky je známo (Newtonův zákon tepelné výměny), že rychlost s jakou klesá teplota tělesa je úměrná teplotnímu rozdílu. Tento rozdíl je \(T-T_0\) (od většího odečítáme menší).

• Veličina \(T\) je teplota tělesa měřená například ve stupních Celsia.
• Veličina \(t\) je čas měřený například v hodinách.
• Derivace \(\frac{\mathrm dT}{\mathrm dt}\) ve stupních Celsia za hodinu je rychlost, s jakou roste teplota tělesa.
  • Pokud je například derivace kladná a rovna hodnotě \(5\) stupňů Celsia za hodinu, znamená to, že teplota roste rychlostí \(5\) stupňů Celsia za hodinu.
  • Pokud je například derivace záporná a rovna hodnotě \(-5\) stupňů Celsia za hodinu, znamená to, že teplota klesá rychlostí \(5\) stupňů Celsia za hodinu.
  • Pokud je derivace dána vztahem \(-e^{-t}\), kde \(t\) je čas v hodinách a derivace vychází ve stupních Celsia za hodinu, využijeme toho, že \(e^0=1\) a \(e^{-1}=0.37\). To znamená, že na počátku se teplota snižuje okamžitou rychlostí jeden stupeň Celsia za hodinu, tato rychlost ochlazování se pozvolna mění a například po hodině se teplota snižuje už jenom rychlostí \(0.37\) stupně Celsia za hodinu.
• Matematickým vyjádřením toho, že rychlost s jakou se mění teplota je úměrná teplotnímu rozdílu \(T-T_0\) je rovnice \[\frac{\mathrm dT}{\mathrm dt}=-k(T-T_0),\] kde \(k\) je konstanta úměrnosti a záporné znaménko vyjadřuje, že teplota klesá. Konstanta \(k\) je číselně rovna rychlosti ochlazování v situaci, kdy je jednotkový rozdíl mezi teplotou objektu a okolí.
• Neznámou v sestavené rovnici je funkce a v rovnici figuruje derivace této funkce. Takové rovnice se naučíme řešit později.

V této chvíli je pro nás cenné to, že umíme přeformulovat fyzikální popis vývoje (rychlost změny teploty je úměrná rozdílu teplot) na kvantitativní popis, kde dokážeme realizovat numerickou simulaci. Realizace takové simulace může vypadat například tak, že na krátký časový krok budeme předpokládat konstantní rychlost. Tuto rychlost použijeme pro odhad nové teploty, tato nová teplota změní teplotní rozdíl, tím se změní i rychlost a postup opakujeme.

Poznámka (smysl příkladu se zákonem ochlazování).

Předchozí příklad je často v různých obměnách používán na modelování ochlazování kávy, což je proces, který většina lidí důvěrně zná. Nemáme pochopitelně ambice se domnívat, že bychom dokázali z této rovnice odvodit nějaké zásadní výsledky aplikovatelné při pití ranní kávy nebo při konzumaci horké polévky. Učíme se na malých věcech, abychom později mohli dělat věci velké. Na známých věcech se učíme aparát, který bude naším jediným nástrojem tam, kde intuice začne selhávat. Z tohoto příkladu je nutné si odnést, že derivace, jako rychlost změny, hraje roli při kvantitativním popisu dějů a při studia procesů, kdy se mění veličiny. Ať už doopravdy (studium pohybu nebo dějů, probíhajících v čase) nebo virtuálně (problémy spojené s mechanikou, včetně statiky, stability a deformací, často pracují s virtuálními změnami, tj. se změnami, které jsou sice z hlediska úlohy přípustné, ale příroda je z nějakého důvodu nerealizuje). Tedy naprostá většina dějů a jevů, které studujeme a chceme jim rozumět. Jakmile se v popisu fyzikálního zákona objeví slovo rychlost, někdy nahrazené souslovím časová změna, znamená to, že kvantitativní popis se děje pomocí derivací.

Derivace funkce dvou proměnných (parciální derivace)

Pokud sledujeme například ve stěně měnící se teplotní profil, zajímá nás, jak se teplota v jednotlivých místech stěny mění v čase a jak se teplota mění v řezu stěnou. Zdá se býti rozumné oddělit obě změny. Buď v daném bodě fixovat polohu a sledovat časový vývoj v tomto bodě, nebo v daném čase udělat něco jako teplotní snímek a srovnávat teplotu ve vybraném bodě s okolními teplotami ve stejném čase. To vede k následujícímu přístupu, kdy u funkce více proměnných sledujeme reakci na změnu jedné jediné veličiny.

Definice (parciální derivace).

Buď \(f\colon \mathbb R^2\to\mathbb R\) funkce dvou proměnných, \(x\) a \(y\), tj. \(f(x,y)\). Výraz \[\frac{\partial f}{\partial x}:=\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}h\] se nazývá parciální derivace funkce \(f\) podle \(x\). Podobně, \[\frac{\partial f}{\partial y}:=\lim_{h\to 0}\frac{f(x,y+h)-f(x,y)}h\] je parciální derivace funkce \(f\) podle \(y\).

Podobně můžeme definovat parciální derivaci pro funkce libovolného konečného počtu proměnných. V těchto parciálních derivacích vlastně sledujeme, jak reaguje veličina \(f\) na změny jenom v jedné proměnné. Proměnná, přes kterou se nederivuje, má vlastně roli parametru a nijak se nemění.

Poznámka (rozšifrování definice derivace).

• Výraz z čitatele, tj. \(f(x+h,y)-f(x,y)\), je změna veličiny \(f\) na intervalu \([x,x+h]\) při konstantní veličině \(y\). Často označujeme též \(\Delta f\).
• Podíl, tj. \(\frac{f(x+h,y)-f(x,y)}h\) je změna veličiny \(f\) na intervalu \([x,x+h]\) při konstantní veličině \(y\), přičemž tato změna je přepočítaná na jednotku veličiny \(x\), tj. v jistém smyslu průměrná rychlost změny vzhledem k \(x\) na intervalu \([x,x+h]\). Často označujeme též \(\frac{\Delta f}{\Delta x}\).
• Limita v definici derivace stahuje délku intervalu, na kterém počítáme průměrnou rychlost, k nule. Tím se z průměrné rychlosti stane okamžitá rychlost. Parciální derivace je tedy okamžitá rychlost s jakou se mění funkce \(f\) při změnách jedné proměnné.

Jednotka derivace \(\frac{\partial f}{\partial x}\) je stejná, jako jednotka podílu \(\frac {f}x\). Jednotka derivace \(\frac{\partial f}{\partial y}\) je stejná, jako jednotka podílu \(\frac {f}y\).

Derivace \(\frac{\partial f}{\partial x}\) udává, jak se mění veličina \(f\) při změnách veličiny \(x\) a předpokladu konstantní veličiny \(y\). Interpretace derivace v nematematických disciplínách je okamžitá rychlost s jakou veličina \(f\) reaguje na změny veličiny \(x\).

Pokud sledujeme vývoj a rozložení teploty na dvourozměrné tepelně vodivé desce, je teplota (udávaná například ve stupních Celsia) funkcí tří proměnných: jedna proměnná je čas \(t\) a dvě proměnné \(x\) a \(y\) jsou souřadnice v rovině. Tedy \(T=T(t,x,y).\) Parciální derivace \(\frac{\partial T}{\partial t}\) udává je rychle (například ve stupních Celsia za hodinu) roste v daném místě teplota. V různých částech desky může být tato veličina jiná a vždy se vztahuje k danému bodu. Může se měnit i v čase, například deska v prostředí s konstantní teplotou postupně dospěje do stavu se stacionárním rozložením teploty, kdy se teplota v žádném místě ani neroste ani neklesá a parciální derivace podle času je nulová. Derivace \(\frac{\partial T}{\partial x}\) udává jak prudce (například ve stupních Celsia na centimetr) roste teplota ve směru osy \(x\).

Rovnice vedení tepla

Videokomentář

Studujme vedení tepla v jednorozměrné tyči. Teplota je funkcí dvou proměnných, polohy a času. Tedy \(T=T(t,x).\) Parciální derivace \(\frac{\partial T}{\partial t}\) udává je rychle (například ve stupních Celsia za hodinu) roste v daném místě teplota. V různých částech desky může být tato veličina jiná a vždy se vztahuje k danému bodu. Přirozeně se mění i v čase, například v prostředí s konstantní teplotou postupně systém dospěje do stavu se stacionárním rozložením teploty, kdy se teplota v žádném místě ani neroste ani neklesá a parciální derivace podle času je nulová. Derivace \(\frac{\partial T}{\partial x}\) udává jak prudce (například ve stupních Celsia na centimetr) roste teplota ve směru osy \(x\).

Poznámka.

Potřebujeme fyzikální zákony řídící vedení tepla. Bez nich matematika model vedení tepla nemá jak naformulovat. Tyto zákony je potřeba matematice dodat “z venku”, z aplikované vědy. Tou je v tomto případě fyzika, jindy může být biologie nebo geologie. Jakmile jsou potřebné zákony a případně materiálové vztahy k dispozici, stává se problém čistě matematickým a fyzika přijde ke slovu při závěrečné interpretaci. Použijeme následující fyzikální fakta.

• Rozdílem teplot je způsoben tok tepla. Velikost toku tepla je úměrná teplotnímu rozdílu a teplo teče z místa v větší teplotou do místa s menší teplotou.
• Teplota se zvyšuje dodáním tepla. Změna teploty je úměrná dodanému teplu.

V dalším už nastupuje matematický popis a ve vhodných chvílích vždy použijeme výše uvedené fyzikální zákony. Mluvíme o teple, ale jako mechanický model si můžeme představit proudění tekutiny (pro jednoduchou představu) nebo proudění vlhkosti (pro odvození rovnice difuze namísto rovnice vedení tepla). Budeme uvažovat libovolné místo materiálu a budeme matematicky vyjadřovat děje, které přispívají ke změně teploty.

• Rychlost s jakou s daném místě roste teplota (v čase) je \[\frac{\partial T}{\partial t}\] a měříme ji například ve stupních Celsia za minutu. Tato rychlost je úměrná rychlosti s jakou do daného místa dodáváme teplo. Proto v dalším budeme hledat rychlost dodávání tepla a daného místa a poté se sem vrátíme a dáme tuto rychlost do souvislosti s rychlostí růstu teploty.
  • Je-li například parciální derivace \(\frac{\partial T}{\partial t}\) rovna \(2^{\circ}\mathrm{C}/\mathrm{min}\), znamená to, že v daném místě roste teplota v čase rychlostí dva stupně Celsia za minutu.
  • Pokud je parciální derivace záporná a rovna například hodnotě \(-2^{\circ}\mathrm{C}/\mathrm{min}\), znamená to, že teplota v tomto místě klesá rychlostí dva stupně Celsia za minutu.
• Rychlost s jakou s daném místě roste teplota jako funkce polohy je \(\frac{\partial T}{\partial x}\) a měříme ji například ve stupních Celsia na centimetr.
  • Je-li například parciální derivace \(\frac{\partial T}{\partial x}\) rovna \(2^{\circ}\mathrm{C}/\mathrm{cm}\), znamená to, že v daném místě roste teplota ve směru osy \(x\) tak, že na každém centimetru naroste o dva stupně Celsia.
  • Pokud je parciální derivace záporná a rovna například hodnotě \(-2^{\circ}\mathrm{C}/\mathrm{cm}\), znamená to, že ve směru osy \(x\) teplota klesá a na každém centimetru klesne o dva stupně Celsia.
• Pro přepočet nerovnoměrného rozložení teploty na tok tepla nás zajímá nikoliv jak teplota v prostoru roste, ale jak klesá. Proto musíme vzít derivaci podle prostorové proměnné záporně, abychom dostali pokles teploty.Tento pokles vynásobíme konstantou, která převede spád teploty na tok tepla. Tuto konstantu označíme \(k\) (nazývá se součinitel tepelné vodivosti a dodá nám ji fyzika, přesněji Fourierův zákon) a tok tepla \(q\) ve směru osy \(x\) je \[q=-k\frac{\partial T}{\partial x}.\] To je veličina, která udává, kolik joulů tepla proteče průřezem za jednotku času.
  • Je-li \(q\) rovno \(7\,\mathrm{J}/\mathrm{min}\) znamená to, že průřezem proteče ve směru osy \(x\) sedm joulů za minutu.
  • Je-li \(q\) záporné a rovno \(-7\,\mathrm{J}/\mathrm{min}\), znamená to, že sedm joulů za minutu proteče v daném místě proti směru osy \(x\).
• Pokud do daného místa přitéká teplo stejnou rychlostí jako odtéká, teplota se nemění a dané místo se ani neohřívá ani neochlazuje. Intenzita ochlazování je dána bilancí mezi přítokem a odtokem. Můžeme si to představit tak, že z tepla které do daného bodu přiteče, se část “oddělí” a přispěje k navýšení teploty a zbytek teče dál. Pro zjištění, kolik tepla se z toku “oddělí” a způsobí v daném místě navýšení teploty potřebujeme vědět, jak rychle v daném místě tok klesá jako funkce proměnné \(x\). Nárůst určíme derivací podle \(x\) a pokles z nárůstu uděláme změnou znaménka. Pokles toku tepla je tedy \[-\frac{\partial q}{\partial x}= -\frac{\partial }{\partial x}\left(-k\frac{\partial T}{\partial x}\right)= \frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right). \]
  • Například pokles \(-\frac{\partial q}{\partial x}=2\,\mathrm{J}/(\mathrm{min}\,\mathrm{cm})\) toku \(q=10\,\mathrm{J}/\mathrm{min}\) znamená, že o centimetr dál ve směru osy \(x\) proteče průřezem směrem doprava už nikoliv deset, ale pouze osm joulů za minutu.
  • Stejný pokles u toku \(q=-10\,\mathrm{J}/\mathrm{min}\) znamená, že v daném místě proteče směrem doleva deset joulů za minutu, ale o centimetr více vpravo je o \(2\) méně, tj. \(-10-2=-12\) a směrem doleva teče dvanáct joulů za minutu.
  • V obou případech intenzita toku klesá podél tohoto toku. Tok slábne.
• Pokles toku vypočtený v předchozím bodě je úměrný rychlosti růstu teploty. Příslušné konstanty úměrnosti dodá fyzika a platí \[\frac{\partial}{\partial x}\left(k\frac{\partial T}{\partial x}\right)=\rho c\frac{\partial T}{\partial t},\] kde \(c\) je měrná tepelná kapacita a \(\rho\) je hustota. (V tomto případě jsou hustota i měrná tepelná kapacita vztaženy ne k jednotce objemu, jak jsme zvyklí, ale k jednotce délky. Například \(\rho\) je lineární hustota, tj. v gramech na centimetr).
  • Například pokles \(-\frac{\partial q}{\partial x}=2\,\mathrm{J}/(\mathrm{min}\,\mathrm{cm})\) toku \(q=10\,\mathrm{J}/\mathrm{min}\) znamená, že o centimetr dál ve směru osy \(x\) proteče průřezem směrem doprava už nikoliv deset, ale pouze osm joulů za minutu. Tedy každou minutu se v jenom centimetru délky od toku “odpojí” energie o velikosti dva jouly a ta se “uloží” do materiálu. Navenek se to projeví ohřevem, přičemž hrají roli fyzikální vlastnosti materiálu.
• Rovnice odvozená v předchozím kroku se nazývá rovnice vedení tepla a dokáže modelovat například prostup tepla stěnou domu. Tato rovnice zachycuje matematicky to, jak funguje vedení tepla.

Shrnutí. V odvození vidíme, že rovnice vedení tepla je vlastně bilance toku tepla. Rozdíl o kolik se v daném místě snižuje tok tepla udává, kolik tepla se v daném místě spotřebovalo. Tato spotřeba tepla se projeví zvýšením teploty v daném bodě.

Poznámka. Vyřešit rovnici vedení tepla je bohužel možné jenom v poměrně speciálních případech, které jsou z praktického hlediska málo významné. Existuje však řada numerických metod jak tuto rovnici vyřešit přibližnými metodami. Tato rovnice je potom “schována” například v softwarech umožňujících vizualizovat tepelné namáhání v okolí kritických prvků staveb, jako jsou okna. Všimněte si univerzálnosti této rovnice. Stejná rovnice, jakou můžeme použít pro posouzení teplotního komfortu ve stavbě, dokáže modelovat například vliv stromu na tepelnou pohodu v městském prostředí nebo prostup tepla do dřeva při jeho tepelné modifikaci.

Numerické derivování

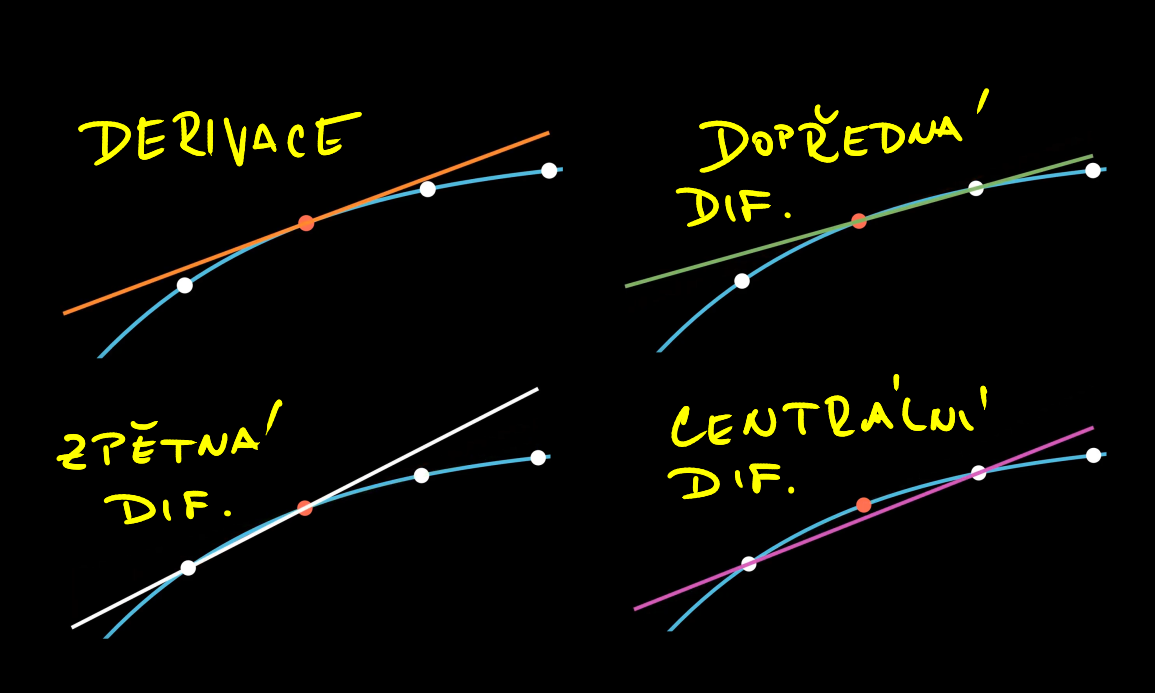
Dopředná diference

Základním přístupem při numerickém odhadu derivace je vynechání limitního přechodu v definici derivace. Pro funkci jedné proměnné a její derivaci \[\frac{\mathrm df}{\mathrm dx}=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\] tedy dostáváme \[\frac{\mathrm df}{\mathrm dx}\approx\frac{f(x+h)-f(x)}{h}.\] Okamžitá rychlost je nahrazena průměrnou rychlostí na intervalu \((x,x+h).\) Tento podíl se nazývá dopředná poměrná diference nebo zkráceně dopředná diference. Pokud použijeme tento postup pro parciální derivace, dostáváme \[\frac{\partial f}{\partial x}\approx\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}\] a \[\frac{\partial f}{\partial y}\approx\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}\]

Zpětná diference

Dopředná diference používá k odhadu bod, ve kterém sledujeme růst a následovníka. Stejně tak je možné použít předchůdce. Tím dostáváme zpětnou diferenci pro funkce jedné proměnné ve tvaru \[\frac{\mathrm df}{\mathrm dx}\approx\frac{f(x)-f(x-h)}{h}.\] a pro parciální derivace ve tvaru \[\frac{\partial f}{\partial x}\approx\frac{f(x,y)-f(x-\Delta x,y)}{\Delta x}\] a \[\frac{\partial f}{\partial y}\approx\frac{f(x,y)-f(x,y-\Delta y)}{\Delta y}\]

Centrální diference

Poznámka (Taylorův polynom).

V diferenciálním počtu funkcí jedné proměnné se zabýváme otázkou hledání nejlepší polynomiální aproximace nějaké funkce. Odpovědí je Taylorův polynom jako nejlepší polynomiální aproximace funkce. S jeho využitím platí \[f(x+h)=f(x)+\frac {\mathrm df(x)}{\mathrm dx}h+\frac{1}{2!} \frac {\mathrm d^2f(x)}{\mathrm dx^2} h^2+O(h^3),\] kde \(O(h^3)\) je funkce, která v okolí nuly konverguje k nule alespoň tak rychle, jako konstantní násobek funkce \(h^3\).

Přesnější aproximace derivace vychází z Taylorova polynomu druhého řádu napsaného pro \(f(x+h)\) a \(f(x-h)\), tj. ze vztahů \[\begin{aligned} f(x+h)&\approx f(x)+f'(x)h+\frac 12 f''(x)h^2,\\ f(x-h)&\approx f(x)-f'(x)h+\frac 12 f''(x)h^2. \end{aligned}\] Pokud tyto vztahy sečteme a odečteme, dostaneme \[\begin{aligned} f(x+h)+f(x-h)&\approx2f(x)+ f''(x)h^2,\\ f(x+h)-f(x-h)&\approx2f'(x)h. \end{aligned}\] Odsud dostáváme aproximace první a druhé derivace \[ f'(x)=\frac{\mathrm d f}{\mathrm dx}\approx \frac{f(x+h)-f(x-h)}{2h} \] a \[ f''(x)=\frac{\mathrm d^2f}{\mathrm dx^2}\approx \frac{f(x-h)-2f(x)+f(x+h)}{h^2}. \] Analogicky pro parciální derivaci podle \(x\) \[ \frac{\partial f}{\partial x}\approx \frac{f(x+h,y)-f(x-h,y)}{2h} \] a \[ \frac{\partial^2f}{\partial x^2}\approx \frac{f(x-h,y)-2f(x,y)+f(x+h,y)}{h^2}. \] Tato aproximace první derivace se nazývá centrální diference a je přesnější, než dopředná diference nebo zpětná diference, protože je založena na přesnější aproximaci funkce \(f\). Používá totiž polynom druhého stupně, kdežto dopředná diference je založena pouze na lineární aproximaci.

WW-otázka

Diskerizace diferenciálních rovnic pomocí konečných diferencí

Rovnice obsahující parciální derivace jsou přirozeným jazykem, kterým modelujeme fyzikální děje. To jsme viděli na rovnici vedení tepla výše a setkáme se s tím i dále. Bohužel tyto rovnice umíme ručně vyřešit jenom v poměrně speciálních případech a i v těchto případech to není snadná práce. Proto v inženýrské praxi dáváme přednost numerickému řešení rovnice. To je založeno na numerické aproximace derivací a převádí řešení rovnic s parciálními derivacemi na řešení lineárních rovnic. Možnosti si naznačíme v následující poznámce, která je čistě informativní a není toho typu, že byste měli umět výpočty v ní uvedené reprodukovat. Je však důležitá pro pochopení, co nám z rovnic vlastně může vyplývat a jeké jsou zhruba požadavky na výpočetní prostředky..

Poznámka (explicitní metoda řešení rovnice vedení tepla).

Po převedení derivací z rovnice vedení tepla \[\rho c\frac{\partial T}{\partial t}=k \frac{\partial ^2 T}{\partial x^2}\] bychom dostali \[\rho c\frac{T(x,t+\Delta t)-T(x,t)}{\Delta t}= k\frac{T(x-\Delta x,t)-2T(x,t)+T(x+\Delta x,t)}{\Delta x^2},\] kde \(\Delta x\) a \(\Delta t\) jsou intervaly oddělující body a časy, ve kterých aproximujeme teplotu. Odsud \[T(x,t+\Delta t)=T(x,t)+\frac{k\Delta t}{\rho c (\Delta x)^2}\Bigl[T(x-\Delta x,t)-2T(x,t)+T(x+\Delta x,t)\Bigr]\] a teplotu \(T(x,t+\Delta t)\) v následujícím časovém okamžiku v libovolném bodě \(x\) dokážeme vypočítat ze současné teploty v tomto bodě a z teploty v sousedních bodech \(x+\Delta x\) a \(x-\Delta x\). Toto je vzorec pro takzvanou explicitní metodu řešení rovnice vedení tepla a tuto metodu je snadné implementovat programovým kódem. Dokonce, pokud teploty v čase \(t\) uspořádáme do sloupcového vektoru \(\vec T(t)\), je možno předchozí vztah zapsat pro všechny body současně jedinou maticovou rovnicí \[\vec T(t+\Delta t)=\vec T(t)+\frac{k \Delta t}{\rho c (\Delta x)^2} A \vec T(t),\] kde \(A\) je matice, která má v hlavní diagonále čísla \(-2\), podél diagonály má čísla \(1\) a jinak nuly s výjimkou prvního a posledního řádku, které jsou nulové. Viz výsledný kód, kde je jenom jeden cyklus pro posun v čase a namísto cyklu přes všechny body v tyči je zde maticové násobení.

Ještě existuje implicitní metoda založená na zpětné diferenci v čase namísto dopředné, tj. \[\frac{\partial T(x,t)}{\partial t}=\frac{T(x,t)-T(x,t-\Delta t)}{\Delta t}\] a odsud \[T(x,t) = T(x,t-\Delta t) +\frac{k\Delta t}{\rho c (\Delta x)^2}\Bigl[T(x-\Delta x,t)-2T(x,t)+T(x+\Delta x,t)\Bigr].\] Toto vztah umožňující výpočet teplot v čase \(t\) z teplot v čase \(t-\Delta t\). Bohužel však v každém tomto vztahu figurují tři teploty v čase \(t\), které ještě neznáme. Úloha vede na řešení soustavy lineárních rovnic, kterých je stejně jako je uvažovaný počet bodů v tyči, tj. v prakticky využitelných úlohách počty začínají řádově stovkami či tisíci a omezeny jsou jenom pamětí počítačů. Každá rovnice v soustavě má sice jenom tři neznámé, ale jako celek je postup komplikovanější na naprogramování i na výpočet. Přesto se ukazuje jako výhodnější, protože je stabilnější a dovoluje řešení počítat po větších časových skocích, než metoda předchozí. Programová relizace je založena na řešení rovnice a v programech Octave nebo Matlab může vypadat následovně. Tento přístup se nazývá implicitní metoda řešení.

Zákon šíření chyb

Videokomentář

Nepřímo měřená veličina je taková, kterou neměříme přímo ale vypočítáváme příslušným vzorcem z jiných naměřených veličin.

• V praxi často měříme nepřímo veličinu \(f\) tak, že měříme veličiny \(x_1\), \(x_2\), \(\dots\), \(x_n\) a hodnotu veličiny \(f\) určíme pomocí vzorce \(f(x_1, x_2, \dots, x_n)\).
• Měření každé z veličin je zatíženo chybou. Je-li chyba veličiny \(x_i\) rovna \(\Delta x_i\), způsobí tato odchylka to, že chyba veličiny \(f\) bude (v souladu se vzorcem pro lineární aproximaci) přibližně \[ \Delta f\approx \left|\frac{\partial f}{\partial x_i}\Delta x_i\right| \]
• Celkovou chybu veličiny \(f\) můžeme určit sečtením chyb způsobených jednotlivými veličinami \(x_i\). Častěji se však používá následující vzorec \[ \Delta f(x_1,x_2,\dots x_n)\approx\sqrt{\left(\frac{\partial f}{\partial x_1}\Delta x_1\right)^2+\left(\frac{\partial f}{\partial x_2}\Delta x_2\right)^2+\cdots+\left(\frac{\partial f}{\partial x_n}\Delta x_n\right)^2}\] označovaný zákon šíření chyb.

Zákon šíření chyb - příklad

Kanadský empirický vzorec pro pocitovou teplotu v zimě (wind-chill factor) je \[W(T,v) = 13.12+0.6215 T-11.37 v^{0.16}+0.3965 T v^{0.16},\] kde \(T\) je teplota (ve stupních Celsia) a \(v\) je rychlost větru (v km/hod). Teplota byla změřena \(-11.0\,{}^\circ\!\text{C}\) s chybou \(0.2\,{}^\circ\!\text{C}\) a rychlost \(26 \,\text{km/hod}\) s chybou \(5\,\text{km/hod}\). S využitím zákona šíření chyb určíme, jaký vliv mají nepřesnosti v měření na nepřesnost vypočítané veličiny.

Dosazením do vzorce dostáváme \(W(-11,26)=-20.212\,{}^\circ\!\text{C}\). Derivováním dostáváme \[\begin{aligned}\frac{\partial W}{\partial T}(T,v)&=0.6215+0.3965 v^{0.16},\\ \frac{\partial W}{\partial v}(T,v)&=-11.37\times 0.16 v^{-0.84}+0.3965 \times 0.16 Tv^{-0.84} \end{aligned} \] a po dosazení \[\begin{aligned}\frac{\partial W}{\partial T}(-11,26)&=1.289,\\ \frac{\partial W}{\partial v}(-11,26)&=-0.163 \,{}^\circ\!\text{C}\, \text{hod}/\mathrm{km}. \end{aligned} \] Za dané teploty a rychlosti větru způsobí nárůst teploty o jeden stupeň nárůst pocitové teploty přibližně o \(1.3\) stupně. Podobně, zesílení větru o jeden kilometr za hodinu způsobí snížení pocitové teploty přibližně o \(0.16\) stupně. Ze zákona šíření chyb dostáváme pro chybu pocitové teploty (dosazováno bez jednotek) \[\Delta W=\sqrt{\left(1.289\times 0.2\right)^2+\left(-0.163\times 5\right)^2}=0.85\,{}^\circ\!\text{C}.\] Pocitová teplota je tedy \(W=-20.2\,{}^\circ\!\text{C}\pm 0.9\,{}^\circ\!\text{C}\).

Online výpočet.