Motivace (stručně).

• Naučíme se efektivně pracovat s libovolně velkými soustavami rovnic.
• Naučíme se zobrazovat vektory na vektory, které nemusí mířit stejným směrem. To vede k novému typu fyzikálních veličin, k tenzorům.

Motivace (podrobněji).

• V předchozích přednáškách jsme se seznámili s derivacemi, s nástroji umožňující převést fyzikální představu o procesech v materiálu do kvantitativní podoby, kdy dokážeme studované jevy kvantifikovat. V praxi však je analytické řešení těchto fyzikálních modelů realizovatelné pouze v nejjednodušších případech. Pro netriviální příklady používáme numerický přístup, který je v mnoha případech nakonec redukován na řešení soustavy rovnic. Tyto soustavy mají typicky obrovské množství rovnic a neznámých (řádově i v jednoduchých aplikacích řádově desetitisíce nebo statisíce rovnic) a proto je nutné mít k dispozici nástroje, umožňující práci s takto obrovskými soustavami rovnic. V této přednášce si představíme nové objekty, matice, se kterými je libovolně velkou soustavu rovnic možno zapsat jako jeden součin tvaru $$AX=B.$$
• V úvodní přednášce jsme naformulovali rovnici vedení tepla jako rovnici, popisující fyzikální podstatu přenosu tepla v materiálu. Tento popis je ve vícerozměrných úlohách nutno zobecnit na dvourozměrný nebo trojrozměrný případ. Potom však u materiálu, který má v různých směrech různé vlastnosti, dochází k tomu, že odezva nemá stejný směr jako podnět. Například u vedení tepla je tok tepla dán směrem poklesu teploty jenom částečně. Vlivem vysoké vodivosti v podélném směru ve srovnání s příčným směrem však je tok tepla odkloněný částečně do podélného směru. Pro popis takového procesu tedy potřebujeme zobrazení, které dokáže změnit nejenom délku, ale i směr vektoru. Toto zobrazení je možné realizovat pomocí matic.

https://youtu.be/cPrmTKdk3yk

Vektory

https://youtu.be/iK6KMeYeTcM

Operace s vektory

Vektorem rozumíme uspořádanou $n$-tici objektů, pro které má smysl operace sčítání a násobení číslem. Počet komponent v této $n$-tici se nazývá dimenze vektoru. Tyto komponenty jsou zpravidla čísla nebo skalární funkce. Aby se s vektory dalo rozumně pracovat, musí tvořit vhodnou strukturu. Například operace musí mít neutrální prvek a každý vektor musí mít opačný prvek.

Definice (vektory, vektorový prostor).

Množinu $V$ uspořádaných $n$-tic $(a_1, a_2,\dots, a_n)$ s operacemi sčítání a násobení reálným číslem definovanými $$\begin{gathered} (a_1, a_2,\dots, a_n)+(b_1, b_2,\dots, b_n)=(a_1+b_1, a_2+b_2,\dots, a_n+b_n)\\ c\cdot (a_1, a_2,\dots, a_n)=(c\cdot a_1, c\cdot a_2,\dots,c\cdot a_n) \end{gathered}$$ pro všechna $c\in\mathbb R$ a $(a_1, a_2,\dots, a_n),(b_1, b_2,\dots, b_n)\in V$ nazýváme vektorovým prostorem. Prvky tohoto prostoru nazýváme vektory. Prvky $a_1, \dots, a_n$ nazýváme složky vektoru $(a_1,a_2,\dots, a_n)$. Číslo $n$ nazýváme dimenze prostoru $V$.

Vektorový prostor, jehož komponenty jsou uspořádané $n$-tice reálých čísel označujeme $\mathbb R^n$.

Často pracujeme se sloupcovými vektory. Zápis je potom přehlednější. $$\begin{pmatrix} 1\cr-2\cr1 \end{pmatrix} + 3 \begin{pmatrix} -1\cr5\cr2 \end{pmatrix} = \begin{pmatrix} 1-3\cr-2+15\cr1+6 \end{pmatrix} = \begin{pmatrix} -2\cr13\cr7 \end{pmatrix}$$

Neutrálním prvkem vzhledem ke sčítání vektorů je nulový vektor $\vec o$, jehož všechny komponenty jsou nulové. Vektor, ke kterému přičteme nulový vektor, se nezmění. $$\vec u +\vec o=\vec u$$

2D a 3D a vektory v geometrii

Modrý vektor je součtem ostatních tří vektorů. U černého vektoru je pravoúhlý trojúhelník pro výpočet délky pomocí Pythagorovy věty. Zdroj: Wikiepdie.

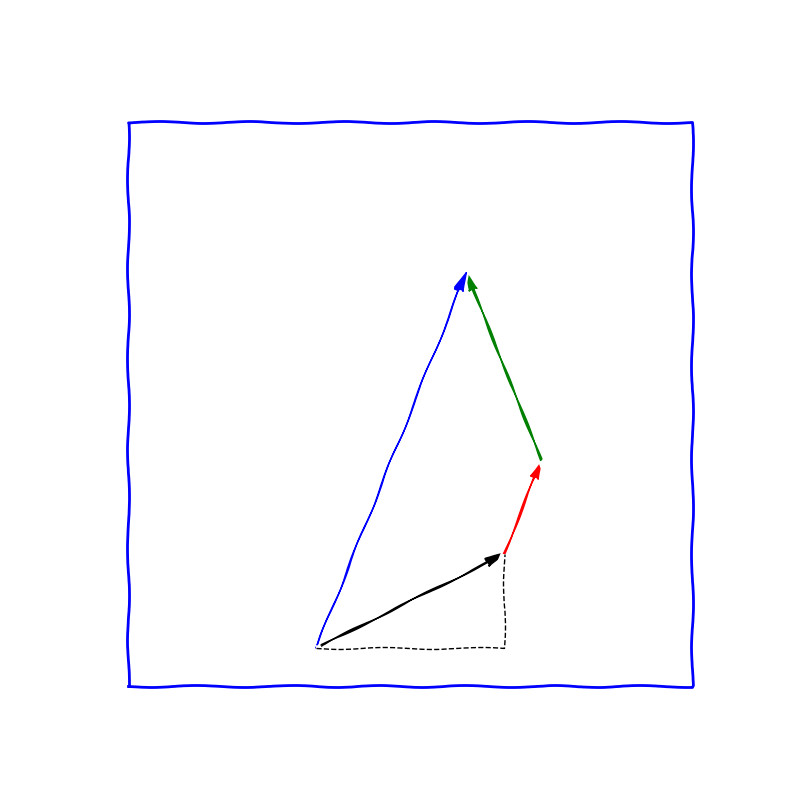
Dvourozměrné vektory s komponentami danými reálnými čísly můžeme reprezentovat graficky pomocí orientovaných úseček. Ve zvolené soustavě souřadnic a při zvoleném výchozím bodu vektor znázorníme takovou orientovanou úsečkou, že komponenty vektoru označují změnu polohy v jednotlivých směrech. Sčítání vektorů odpovídá posunutí počátečního bodu druhého vektoru do koncového bodu prvního vektoru a nahrazení dvou částečných posunutí jedním celkovým. Je přirozené zavést délku vektoru $\vec u= \begin{pmatrix} u_1\\u_2 \end{pmatrix}$ pomocí Pythaghorovy věty vzorcem $|\vec u|=\sqrt{u_1^2+u_2^2}$. Násobení vektoru kladným číslem odpovídá změně délky vektoru. Násobení záporným číslem odpovídá změně délky a otočení směru.

Lineární kombinace

Definice (lineární kombinace).

Nechť $\vec u_1$, $\vec u_2$, $\dots$ $\vec u_k$ je konečná posloupnost vektorů z vektorového prostoru $V$. Vektor $\vec u$, pro který platí $$\vec u=t_1\vec u_1+t_2\vec u_2+\cdots +t_k \vec u_k,$$ kde $t_1$, $t_2$, $\dots$, $t_k$ jsou nějaká reálná čísla, se nazývá lineární kombinace vektorů $\vec u_1$, $\vec u_2$, $\dots$, $\vec u_k$. Čísla $t_1$, $t_2$, $\dots$, $t_k$ nazýváme koeficienty lineární kombinace.

Výpočet lineární kombinace si můžete vyzkoušet online.

ww2:problems/vektory/linearni_kombinace.pg

Stejný modrý vektor vyjádřený ve dvou různých bázích ve 3D, v červené a fialové bázi. Bázové vektory volíme zpravidla jednotkové délky, na obrázku už jsou vynásobeny vhodnými konstantami tak, abychom jako lineární kombinaci obdrželi požadovaný vektor. Zdroj: Wikipedia.

Příklad. Lichoběžníkové pravidlo $$\int_a^bf(x)\,\mathrm dx\approx \frac h2\Bigl( {y_0}+2y_1+2y_2+\cdots+2y_{n-1}+{y_n}\Bigr).$$
ukazuje, že určitý integrál je možno aproximovat lineární kombinací funkčních hodnot na pravidelné mřížce rozdělující obor integrace. Koeficienty lineární kombinace jsou dvojky s vyjímkou prvního a posledního koeficientu, které jsou jednotkové. Existují i další aproximační vzorce, které používají jiné koeficienty a jsou založeny například na aproximaci funkce parabolami namísto přímek.

Příklad. V metodě konečných diferencí (viz druhá přednáška o derivacích) se derivace aproximují výrazy, které jsou lineární kombinací po sobě jdoucích funkčních hodnot hledané funkce na pravidelné mřížce délky $h$. Pro konkrétnost, pro první derivaci máme $$\frac{\mathrm df}{\mathrm dx}\approx\frac{f(x+h)-f(x-h)}{2h} =\frac 1{2h}f(x+h)-\frac 1{2h}f(x-h),$$ a pro druhou derivaci $$\frac{\mathrm d^2f}{\mathrm dx^2}\approx\frac{f(x-h)-2f(x)+f(x+h)}{h^2}=\frac{1}{h^2} f(x-h) - \frac{2}{h^2} f(x) + \frac{1}{h^2} f(x+h).$$

Model migrace jako přepínání stavů

Markovovy řetězce umožňují modelování situací, ve kterých dochází k přepínání stavů. Například migrace mezi městem a venkovem. Zdroj: pixabay.com

Na příkladě si ukážeme, kdy je přirozené pracovat s lineárními kombinacemi vektorů. Pokusíme se na jednoduchém modelu migrace mezi městem a venkovem demonstrovat přístup, který se používá v případech, kdy je možné rozdělit jednotlivé části systému do konečného počtu navzájem disjunktních stavů a jednotlivé části mohou měnit svůj stav, přičemž pravděpodobnost změny je dána pouze současným stavem a ne například historií předchozích stavů. Aplikace zahrnují například modelování vegetace na stanovištích (zájmová oblast je rozdělena na stanoviště a ke každému stanovišti je přiřazen převažující typ vegetace), pro modelování změn druhového složení v lese nebo v krajině, ale i v hydrologických modelech, předpovědi počasí a jinde. Základní model má řadu rozšíření a ukážeme si jej jen v nejjednodušší formě a na případě dvou stavů.

Slovní formulace: Každý rok měříme velikosti populací ve městě a na venkově. Na počátku $60\%$ populace žije ve městě a $40\%$ na venkově. Každý rok zůstane $95\%$ městské populace ve městě a $5\%$ se stěhuje na venkov. Podobně $97\%$ obyvatelstva venkova zůstává a $3\%$ se stěhuje do města.

Matematický model: Procentuální složení zaznamenáváme ve formě vektoru. Na počátku bude $$\vec q_0= \begin{pmatrix} 0.6 \\ 0.4 \end{pmatrix}.$$ Po jednom roce je rozložení populace dáno vektorem $$\vec q_1= \begin{pmatrix} 0.95 \\ 0.05 \end{pmatrix} 0.6 + \begin{pmatrix} 0.03 \\ 0.97 \end{pmatrix} 0.4 .$$ Intenzita migrace jednotlivými směry je ve sloupcových vektorech na pravých stranách. Koeficienty v této lineární kombinaci jsou koeficienty vektoru $\vec q_0$.

Podobně, rozložení po dvou letech bude dáno lineární kombinací s koeficienty, danými vektorem $\vec q_1$. Pokud bychom potřebovali znát rozložení populace po $k$ letech, situace se komplikuje. Dostali bychom rekurentní vzorec, který je nutno stále opakovat. Pro odstranění tohoto nepohodlí se zavádí pojem matice, viz níže.

Lineární závislost a nezávislost vektorů

V $n$-rozměrném prostoru existuje $n$-tice vektorů, pomocí nichž můžeme dostat libovolný vektor jako lineární kombinaci. Taková $n$-tice se nazývá báze. Dá se ukázat, že bází je nekonečné mnoho a pro zadanou bázi a vektor je vyjádření vektoru pomocí bázových vektorů jednoznačné až na pořadí. Nejjednodušší báze je tvořena jednotkovými vektory, které mají všechny komponenty kromě jedné nulové. Například pro bázové vektory $\vec e_1=(1,0)$ a $\vec e_2=(0,1)$ dvourozměrného vektorového prostoru a pro vektor $\vec v=(4,3)$ platí $$\vec v=(4,3)=(4,0)+(0,3) = 4 (1,0) +3 (0,1) = 4\vec e_1+3 \vec e_2.$$ Koeficienty lineární kombinace se nazývají souřadnice. Například souřadnice vektoru $\vec v=(4,3)$ v uvažované bázi jsou $\begin{bmatrix} 4\\3 \end{bmatrix}_{e_1,e_2}$. Pro bázové vektory $\vec \varepsilon_1=(2,1)$ a $\vec \varepsilon_2=(0,1)$ platí $$\vec v=(4,3)=2(2,1)+1(0,1)=2\vec \varepsilon_1+\vec \varepsilon_2$$ a souřadnice vektoru $\vec v=(4,3)$ v nové bázi jsou $\begin{bmatrix} 2\\1 \end{bmatrix} _{\varepsilon_1,\varepsilon_2}$. Tady vidíme výhodu “pěkné volby” bázových vektorů v prvním případě. Tam jsou souřadnicemi přímo komponenty vektoru.

Aby použití souřadnic mělo smysl, musí existovat jediná možnost jak daný vektor vyjádřit pomocí lineární kombinace zadaných bázových vektorů. Tato úloha se dá redukovat na úlohu, zda taková jednoznačnost existuje u nulového vektoru. Tím je motivována následující úvaha a z ní vyplývající definice.

Výsledkem triviální lineární kombinace, tj. lineární kombinace s nulovými koeficienty, je nulový vektor. Pro některé vektory můžeme nulový vektor dostat i jako jinou lineární kombinaci, než je ta triviální. Ukazuje se, že je důležité identifikovat tyto případy a pro rozlišení toho, zda se nulový vektor dá nebo nedá vyjádřit jako netriviální lineární kombinace zavedeme nové pojmy, lineární závislost a nezávislost.

Definice (lineární závislost a nezávislost).

Řekneme, že vektory $\vec u_1$, $\vec u_2$, $\dots$, $\vec u_k$ jsou lineárně závislé, jestliže existuje alespoň jedna netriviální lineární kombinace těchto vektorů, jejímž výsledkem je nulový vektor $\vec o$, tj. existují-li reálná čísla $t_1$, $t_2$, $\dots$, $t_k$, z nichž alespoň jedno je různé od nuly, taková, že platí $$\vec o=t_1\vec u_1+t_2\vec u_2+\cdots +t_k \vec u_k.$$ V opačném případě říkáme, že vektory jsou lineárně nezávislé.

Platí následující.

• Vektory, které tvoří bázi, jsou lineárně nezávislé.
• Je-li vektorů větší počet, než je dimenze prostoru, jsou tyto vektory lineárně závislé.
• Je-li v posloupnosti vektorů některý vektor násobkem jiného vektoru nebo lineární kombinací ostatních vektorů, jedná se o lineárně závislou posloupnost vektorů.

Ve výše uvedených případech poznáme lineární závislost snadno. Mimo tyto případy je to snadné pouze pro dvojici vektorů, které jsou lineárně závislé právě tehdy když je jeden vektor násobkem druhého. V tom případě říkáme, že vektory mají stejný směr. V ostatních případech se lineární závislost a nezávislost naučíme posuzovat později při výpočtu hodnosti.

Pootočení vektoru

https://youtu.be/7vyBwmZZ3Pg

Jednotkové vektory ve směru os pootočíme o úhel $\theta$ a výsledek vyjádříme jako lineární kombinaci původních vektorů.

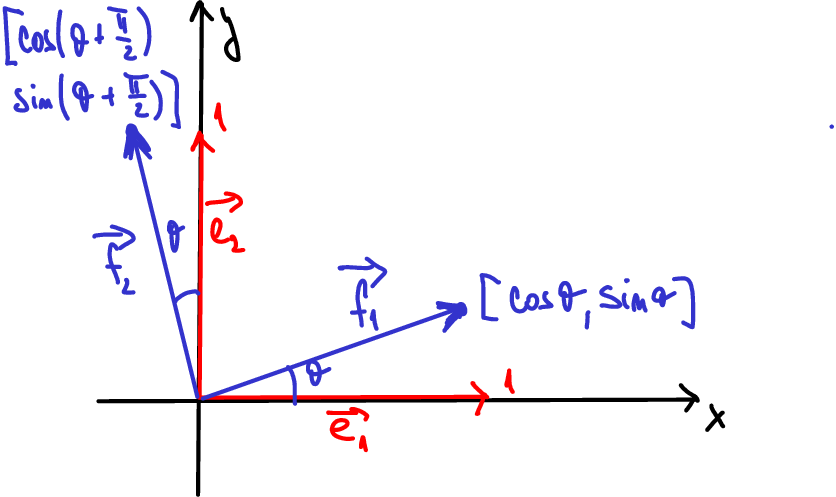
Ve dvourozměrném vektorovém prostoru uvažujme jednotkové vektory ve směru souřadných os $\vec e_1=(1,0)$ a $\vec e_2=(0,1)$. Pokud pootočíme vektory o úhel $\theta$ v kladném směru, mají pootočené vektory $\vec f_1$, $\vec f_2$ souřadnice $$\vec f_1=(\cos \theta,\sin\theta)$$ (plyne přímo z definice funkcí sinus a kosinus na jednotkové kružnici) a $$\vec f_2=(-\sin\theta,\cos\theta)$$ (plyne z předchozího přičtením úhlu $\frac\pi 2$ a využitím identit $\cos\left(\theta+\frac\pi 2\right)=-\sin\theta$ a $\sin\left(\theta+\frac\pi 2\right)=\cos\theta$). Pomocí lineární kombinace můžeme psát $$\begin{aligned} \vec f_1&=\cos(\theta) \vec e_1 +\sin(\theta)\vec e_2,\\ \vec f_2&=-\sin(\theta)\vec e_1 +\cos(\theta)\vec e_2. \end{aligned}$$ Je-li úhel $\theta$ malý, platí (viz cvičení z derivací) $\sin\theta\approx\theta$, $\cos\theta\approx 1$ a dostáváme $$\begin{aligned} \vec f_1&= (1,\theta) = \vec e_1 +\theta\vec e_2,\\ \vec f_2&= (-\theta,1) = -\theta\vec e_1 +\vec e_2. \end{aligned}$$

Matice

https://youtu.be/DY044M_RbVs

Matice a jejich lineární kombinace

Definice (matice).

Maticí řádu $m\times n$ rozumíme schema $$A= \begin{pmatrix} a_{11}& a_{12}& a_{13}& \cdots{}& a_{1n}\\ a_{21}& a_{22}& a_{23}& \cdots{}& a_{2n}\\ \vdots{}& \vdots{}& {}& \ddots{}& \vdots{}\\ a_{m1}& a_{m2}& \cdots{}& \cdots{}& a_{mn} \end{pmatrix}$$ kde $a_{ij}$ pro $i=1..m$ a $j=1..n$ jsou reálná čísla nebo funkce. Množinu všech matic řádu $m\times n$, jejichž prvky jsou reálná čísla, označujeme symbolem $\mathbb R^{m\times n}$. Zkráceně zapisujeme též ${A=(a_{ij})}$.

Je-li $m=n$ nazývá se matice $A$ čtvercová matice, jinak obdélníková matice. Je-li $A$ čtvercová matice, nazýváme prvky tvaru $a_{ii}$, tj. prvky, jejichž řádkový a sloupcový index jsou stejné, prvky hlavní diagonály.

ww2:problems/matice/prvky_matice.pg

Pro matice definujeme sčítání a násobení číslem stejně jako u vektorů, tj. po složkách. Má potom smysl mluvit o lineární kombinaci matic a o jejich lineární závislosti či nezávislosti. Tyto operace přirozeně přebírají všechny důležité vlastnosti operace sčítání, jako jsou asociativita, komutativita, existence neutrálního prvku nebo existence opačného prvku.

V této fázi je vlastně jedno, jestli prvky jsou uspořádány jako řádkový nebo sloupcový vektor nebo jako matice. Odlišení matic a vektorů provedeme zavedením maticového součinu.

Maticový součin

Definice (součin matic).

Buďte $A=(a_{ij})$ matice řádu $m\times n$ a $B=(b_{ij})$ matice řádu $n\times p$. Součinem matic $A$ a $B$ (v tomto pořadí) rozumíme matici $G=(g_{ij})$ řádu $m\times p$, kde $$g_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj}$$ pro všechna $i=1..m$, $j=1..p$. Zapisujeme $${G=AB}$$ (v tomto pořadí).

Slovy: v $j$-tém sloupci matice $AB$ je lineární kombinace sloupců matice $A$, přičemž koeficienty této lineární kombinace jsou prvky z $j$-tého sloupce matice $B$.

Na maticový součin můžeme pohlížet i pomocí pojmů známých z analytické geometrie. Prvky v součinu matic jsou skalárními součiny řádků první matice se sloupci druhé matice.

Maticový součin

• je asociativní $$(AB)C=A(BC)=ABC,$$
• je distributivní vzhledem ke sčítání $$A(B+C)=AB+AC\qquad \text {a}\qquad (B+C)A=BA+CA,$$
• není však komutativní ($AB$ je obecně různé od $BA$, proto v předchozím máme roznásobování závorky zleva i zprava),
• ale při násobení skalárem komutativní je: $$A(\lambda B)=\lambda (AB),$$ kde $\lambda$ je reálné číslo a $A$ a $B$ jsou matice.

Můžeme tedy měnit uzávorkování, můžeme roznásobovat závorky, nesmíme však měnit pořadí matic při násobení.

Neutrální prvek maticového součinu

U každé operace nás zajímá neutrální prvek, což je prvek, který se v dané operaci nijak neprojeví. Třeba u sčítání čísel je neutrálním prvkem nula, při násobení čísel je neutrálním prvkem jednička. Pokud nějaký prvek potřebujeme zapsat ve tvaru součinu, zapíšeme ho jako součin sebe sama s jedničkou. To využijeme například při vytýkání ve kterém u vytýkaného prvku nefiguruje v některém členu druhý součinitel, jako třeba ve výpočtu $$3x^2+x=3x \cdot x + 1\cdot x = (3x+1)\cdot x.$$ Ukážeme si, že podobný neutrální prvek existuje i u násobení matic a trik podobný výše uvedenému využijeme později, až budeme mluvit o vlastních vektorech matice.

Neutrálním prvkem při násobení matic čtvercových je čtvercová matice, která má jedničky v hlavní diagonále a nuly mimo tuto diagonálu. Tato matice se nazývá jednotková matice a označuje $I$. Mají-li čtvercové matice $A$ a $I$ stejný počet řádků a sloupců, platí $$AI=IA=A.$$

Například pro matice $3\times 3$ je jednotková matice $$I= \begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix} .$$ Je-li $A$ matice $3\times 3$, kterou násobíme zprava maticí $I$, výsledná matice $AI$ bude mít tři sloupce (matice $I$ má tři sloupce), v prvním sloupci bude první sloupec matice $A$ (lineární kombinace sloupců matice $A$ s koeficientem 1 pro první sloupec a koeficienty 0 pro všechny další sloupce) atd. Jako výsledek součinu dostaneme přirozeně matici $A$. Že stejný výsledek dostaneme i pro opačné pořadí v součinu je možné pro nějaký konkrétní případ ověřit přímo a že toto funguje obecně se nejsnáze ukáže, až si představíme operaci transponování matice a její vztah k maticovému součinu.

Výpočet operací s maticemi je nejlepší se naučit při výpočtu konkrétních příkladů. Ty si můžete vyzkoušet online na následujících odkazech.

ww2:problems/matice/soucet_matic.pg

ww2:problems/matice/soucin_matic.pg

ww2:problems/matice/soucin_matice_a_vektoru.pg

Aplikace maticového součinu 1/3

Nejdůležitější aplikací maticového součinu je to, že pomocí maticového součinu je možné vyjádřit zobrazení, kde na vstupu i na výstupu jsou vektorové veličiny. To umožní rozšířit fyzikální zákony na anizotropní látky (různé vlastnosti v různých směrech, například dřevo nebo obecně látky vykazující uspořádanou strukturu). Kromě fyzikálních veličin, které mají číselnou hodnotu (skaláry) nebo číselnou hodnotu a směr (vektory) tak získáváme další fyzikální veličiny, tenzory. Více viz níže a též podkapitola “Matice jako zobrazení v materiálovém inženýrství”.

Je-li druhá matice v součinu sloupcový vektor $\vec u$, je výsledkem maticového součinu matice $A$ a tohoto vektoru opět sloupcový vektor $A\vec u$. Matici je tedy možné chápat jako zobrazení, kdy vektoru $\vec u$ je přiřazen vektor $\vec v$ vztahem $$\vec v = A\vec u.$$ Tento vztah je možné chápat jako přímé rozšíření vztahu pro přímou úměrnost mezi veličinami. Zobecnění je v tom, že obě veličiny mezi nimiž je vztah úměrnosti jsou vektorovými veličinami a konstanta úměrnosti je matice. Ve fyzice tato matice mívá ještě některé speciální vlastnosti související například s tím, že fyzikální zákony nezávisí na volbě souřadné soustavy a proto se takové matice nazývají tenzory (přesněji tenzory druhého řádu). Používáme je pro popis zobrazení mezi vektory, které nezachovává směr vektoru. Například studium transportních dějů v anizotropních materiálech (tj. například vedení tepla ve dřevě nebo difuze ve dřevě).

Aplikace maticového součinu 2/3

https://youtu.be/4jqBoskZ9Ak

Derivace diskrétní funkce

V metodě konečných diferencí jsme si ukázali a v předcházejícím textu připomněli, že derivace umíme aproximovat výrazy, které jsou lineární kombinací po sobě jdoucích funkčních hodnot hledané funkce na pravidelné mřížce délky $h$. Toto je možné vyjádřit pomocí maticového součinu. Pro konkrétnost, pro druhou derivaci aproximujeme pomocí tří po sobě jdoucích hodnot v ekvidistantních krocích vzorcem $$f''(x)\approx\frac{1}{h^2} f(x-h) - \frac{2}{h^2} f(x) + \frac{1}{h^2} f(x+h).$$ Tento vztah můžeme chápat jako lineární kombinaci hodnot $$\frac 1{h^2}, \quad -\frac{2}{h^2}, \quad \frac 1{h^2}$$ s koeficienty $$f(x-h), \quad f(x), \quad f(x+h).$$ Pokud je například funkce $f(x)$ na intervalu $I$ dána funkčními hodnotami $f(x_1)$, $f(x_2)$, $f(x_3)$, $f(x_4)$, $f(x_5)$ v bodech rovnoměrně rozmístěných ve vzdálenosti $h$ od sebe, můžeme vypočítat druhé derivace $f''(x_2)$, $f''(x_3)$ a $f''(x_4)$ pomocí vztahů $$f''(x_2)\approx\frac{1}{h^2} (f(x_1) - 2 f(x_2) + f(x_3))$$ $$f''(x_3)\approx\frac{1}{h^2} (f(x_2) - 2 f(x_3) + f(x_4))$$ a $$f''(x_4)\approx\frac{1}{h^2} (f(x_3) - 2 f(x_4) + f(x_5)).$$ Tyto tři rovnice je možnou zapsat jediným vztahem pomocí maticového násobení $$\begin{pmatrix}f''(x_2)\\f''(x_3)\\f''(x_4)\end{pmatrix} =\frac 1{h^2}\begin{pmatrix} 1 & -2 & 1& 0& 0\\ 0& 1 & -2 & 1& 0\\ 0& 0 & 1 & -2 & 1\\ \end{pmatrix} \begin{pmatrix}f(x_1)\\f(x_2)\\f(x_3)\\f(x_4)\\f(x_5)\end{pmatrix}.$$ Proto matice $$\begin{pmatrix} -2 & 1& 0& 0 & 0\\ 1 & -2 & 1& 0& 0\\ 0& 1 & -2 & 1& 0\\ 0& 0 & 1 & -2 & 1\\ 0& 0& 0 & 1 & -2 \\ \end{pmatrix}$$ hraje důležitou roli v numerické matematice při numerickém modelování fyzikálních dějů. Až na první a poslední řádek se jedná o matici, která umí zprostředkovat numerické derivování funkce. První a poslední řádek se přidávají, aby matice získala čtvercový tvar a jistou míru symetrie. (Symetrickým maticím se budeme věnovat za chviličku.) Tyto dva přidané řádky se uplatní při formulaci okrajových podmínek definujících chování funkce na koncích intervalu.

Pomocí maticového součinu dokážeme reprezentovat libovolné zobrazení, které zachovává součet a násobení konstantou, mezi něž derivování patří. Jiný přístup k maticové formulaci derivace, k derivování na množině polynomů, si ukážeme ve cvičení.

Markovovy řetězce

Markovovy řetězce umožňují modelování situací, ve kterých dochází k přepínání stavů. Například migrace mezi městem a venkovem. Zdroj: pixabay.com

Budeme pokračovat v příkladě s migrací. Viděli jsme, že po jednom roce je tedy rozložení populace dáno vektorem $$\vec q_1=0.6 \begin{pmatrix} 0.95 \\ 0.05 \end{pmatrix} +0.4 \begin{pmatrix} 0.03 \\ 0.97 \end{pmatrix}.$$ Koeficienty vektoru $\vec q_0=\begin{pmatrix} 0.6\\0.4 \end{pmatrix}$ jsou koeficienty v této lineární kombinaci. To lze zapsat jako maticový součin $$\vec q_1= \begin{pmatrix} 0.95 & 0.03 \\ 0.05 & 0.97 \end{pmatrix} \begin{pmatrix} 0.6\\0.4 \end{pmatrix}.$$ Pro další rok tento postup opakujeme. Pro matici $A=\begin{pmatrix} 0.95 & 0.03 \\ 0.05 & 0.97 \end{pmatrix}$ platí $$\vec q_1=A\vec q_0.$$ Je-li $\vec q_k$ vektor charakterizující rozložení po $k$ letech, rozložení v následujícím roce získáme ze vztahu $$\vec q_{k+1}=A\vec q_k.$$ Pro stav po dvou letech platí $$\vec q_2=A\vec q_1=A(A \vec q_0)=(AA)\vec q_0=A^2 \vec q_0.$$ Po $k$ letech je rozložení populace dáno vektorem $$\vec q_k=A^k \vec q_0.$$ Pokud pro některý vektor $\vec q$ platí $$\vec q=A\vec q$$ znamená to, že systém je ve stacionárním stavu a procentuální zastoupení stavů se nemění. Například v našem modelu to znamená, že stejný počet lidí přestěhovaných z města do vesnice je stejný, jako počet lidí přestěhovaných opačným směrem. Tento stacionární stav se dá najít opakovanými iteracemi z náhodného výchozího stavu. Online výpočet.

Takový rekurentní vzorec je možno chápat jako jakýsi stavový automat, který řídí přepínání mezi dvěma stavy (obyvatel města, obyvatel vesnice). V matematice se nazývá Markovův řetězec. Protože uvnitř matice jsou pravděpodobnosti a v každém sloupci vždy nastane právě jeden z jevů, který tyto pravděpodobnosti reprezentují, je součet čísel v každém sloupci matice roven jedné. V obecných stavových modelech, kde se nepracuje s pravděpodobností, jako je například Leslieho model růstu populace níže, tato podmínka platit nemusí.

(Podle D. Lay, Linear algebra. Markovovy řetězce viz též Wikipedie, ale pozor: někdy se místo zde představeného zápisu používá zápis s řádkovým vektorem nalevo od matice popisující změnu stavů.)

Růst populace pomocí Leslieho matice

Patrick Holt Leslie (1900-1972) roku 1945 publikoval v časopisu Biometrika On the use of matrices in certain population mathematics. V něm sestavil a analyzoval model růstu počtu samic v populaci potkanů (Rattus norvegicus); jeho model ovšem může být stejně dobře použit pro lidskou nebo jinou populaci. Zdroj: pixabay.com

Leslieho model používá matice pro modelování vývoje populace, který zohledňuje věkovou strukturu populace. Model předpokládá, že populace je rozdělena do několika věkových kategorií a v každé kategorii je dána pravděpodobnost dožití se do další kategorie a průměrný počet potomků. Situace je podobná jako u Markovova řetězce s tím, že nenulový prvek matice bude jenom tam, kde dochází k přesunu do další věkové kategorie nebo tam, kde kumulujeme počet nově narozených jedinců v nejnižší věkové kategorie pro jednotlivé věkové skupiny rodičů.

Příslušný model například pro populaci rozdělenou do tří věkových kategorií by byl dán rovnicí $$\begin{pmatrix} x_1(k+1) \\ x_2(k+1) \\ x_3 (k+1) \end{pmatrix} = \begin{pmatrix} f_1 & f_2 & f_3 \\ p_1 & 0 & 0\\ 0 & p_2 & 0 \end{pmatrix} \begin{pmatrix} x_1(k) \\ x_2(k) \\ x_3 (k) \end{pmatrix}$$

Opakovaným násobením získáme věkovou strukturu populace v další generaci a toto se opakuje podobně jako u Markovova řetězce.

Původně byl Leslieho model odvozen pro modelování populace samic, dá se však adaptovat na populaci obecně.

Další informace:

• Z. Pospíšil, Maticové populační modely

Analýza sítí a toků v sítích

Jednoduchý potravní řetezec. Zdroj: https://linearalgebraapplications19.wordpress.com/2019/04/29/food-webs/

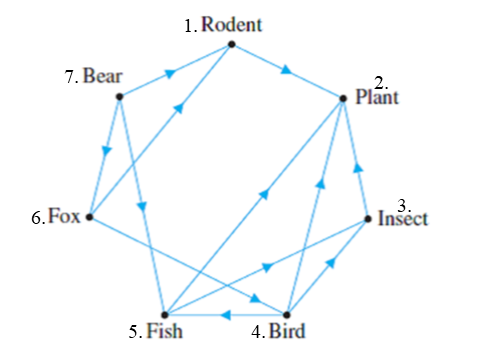
Matice je možné použít k analýze sítí a toků v sítích, kdy sítí rozumíme například potravní řetězec, kaskádu chemických a biochemických reakcí představujících metabolismus živého organismu a podobně. Matice umožňují hledat v sítích zákonitosti a vazby, umožňují modelovat toky mezi uzly v sítích, umožňují provádění experimentů v počítači namísto laboratoře. To zrychluje, zlevňuje a zefektivňuje práci a umožňuje automatizaci a hlubší studium.

Jednoduchá ukázka potravní sítě je na obrázku a tato síť by se dala charakterizovat maticí $$A=\begin{pmatrix} 0&1&0&0&0&0&0\\ 0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0\\ 0&1&1&0&1&0&0\\ 0&1&1&0&0&0&0\\ 1&0&0&1&0&0&0\\ 1&0&0&0&1&1&0 \end{pmatrix}$$ Je-li například vektor $v$ sloupcový vektor ze samých jedniček, potom vektor $Av$ udává počet přímých potravních zdrojů pro každý druh v řetězci. Podobně, vektor $A^2v$ udává počet nepřímých potravních zdrojů přes jednoho zprostředkovatele. Více viz blogový zápisek Food Webs.

Analogicky bývají studovány metabolické sítě, kde místo vztahů jsou chemické reakce a prvky matice označují, které produkty v jakém množství vstupují do těchto reakcí (stoichiometrické koeficienty). Je-li $X$ sloupcový vektor označující množství jednotlivých metabolitů, $v$ sloupcový vektor označující rychlosti jednotlivých reakcí a $A$ matice stoichiometrických koeficientů, platí $$\frac{\mathrm dX}{\mathrm dt}=Av,$$ kde derivaci vektoru chápeme po složkách jako vektor sestavený z derivací jednotlivých komponent. Viz například Basic concepts and principles of stoichiometric modeling of metabolic networks

Reálné sítě mají tisíce uzlů a tisíce vztahů mezi nimi a není možné je studovat jinak, než matematickými metodami. Například model Escherichia Coli, hojně studované bakerie, obsahuje 1805 metabolitů, 2583 reakcí a 1367 genů. Matice umožňují studovat nejenom vztahy ale i intenzitu toku mezi jednotlivými metabolity a umožní studovat vliv vnějších zásahů, například knokautování některých genů nebo umístění bakerie do anaerobního prostředí. V příkladě s potravním řetězcem například můžeme (po dodání dalších informací do modelu) určit, jakým procentem se jednotlivé složky potravy podílí na celkovém jídelníčku a jak se toto složení změní při odstranění nějaké složky potravy.

Aplikace maticového součinu 3/3: matice jako zobrazení, tenzory

https://youtu.be/7NH8p323zxo

Nyní se na zobrazení pomocí matice podíváme očima geometra a poté očima materiálového inženýra. Matici budeme chápat jako objekt, který je možné vynásobit s vekorem a získat jiný vektor. V určitém smyslu jde tedy o zobrazení, kdy vzory i obrazy jsou vektory.

Matice jako zobrazení v geometrii

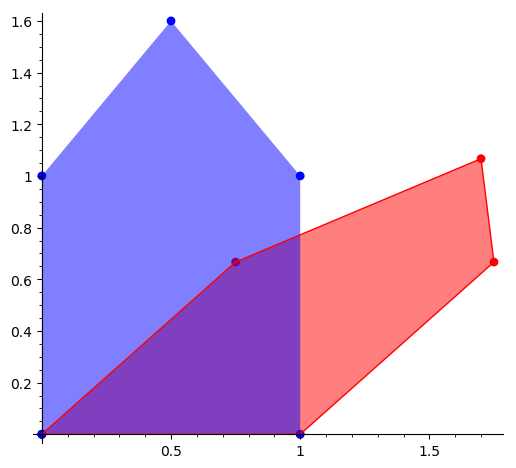
manimp:MatrixMultiplication|Nejdůležitější rolí matic v materiálovém inženýrství je jejich schopnost jistým způsobem transformovat vektory (body) prostoru. Přesněji, zobrazení zachovává rovnoběžnost a dělící poměr. Rovnoměrně rozmístěná mřížka se zobrazí zase na rovnoměrně rozmístěnou mřížku. (První část prezentace).

Příklad transformace dané maticí. Zachovává se například rovnoběžnost a středy úseček. Přímky se zobrazují na přímky.

Transformace 3D objektu do roviny pomocí matice. Koeficienty matice můžou realizovat libovolné natočení.

Je-li $A$ čtvercová matice, můžeme každému vektoru $\vec q$ přiřadit vektor $Y=A\vec q$ a tím definovat zobrazení $n$-rozměrného prostoru do sebe. Dá se ukázat, že takto dostaneme všechna zobrazení, která zobrazují úsečky na úsečky, počátek nechávají v počátku a jsou pěkná v tom smyslu, že zachovávají středy úseček, rovnoběžnost a lineární kombinaci vektorů. Ukázka zobrazení ve 2D.

Podobně je možné definovat i zobrazení mezi prostory jiných dimenzí. Například projekce 3D objektu do 2D. Protože zobrazení zachovává rovnoběžnost, není možné takto jednoduše obdržet například perspektivu. Protože se zachovává počátek, není možné zahrnout ani posunutí. V obou případech si pomáháme trikem, že přidáme další souřadnici, více viz Wikipedie a heslo Grafické transformace nebo Camera matrix.

Například matice $$R_\theta= \begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix}$$ zobrazí vektory $e_1=(1,0)$ a $e_2=(0,1)$ na $$\begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} 1\\0 \end{pmatrix} = \begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix}$$ a $$\begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} 0\\1 \end{pmatrix} = \begin{pmatrix} -\sin\theta \\ \cos\theta \end{pmatrix}.$$ Proto matice $R_\theta$ definuje zobrazení, které pootočí rovinu o úhel $\theta$ a nazývá se matice rotace. Matice malých rotací je (použitím lineární aproximace $\sin\theta\approx \theta$ a $\cos \theta\approx 1$ v okolí nuly) $$R_{\theta,0}= \begin{pmatrix} 1 & - \theta\\ \theta & 1 \end{pmatrix}.$$ Tuto matici budeme potřebovat při studiu deformace při odvození matematického popisu malých deformací.

Matice jako zobrazení v materiálovém inženýrství

Na poli voda teče v podstatě z kopce, ale brázdy tvořící strukturu pole můžou směr stáčet a případně tok zpomalovat. Totéž se může dít a děje v řadě porézních materiálů. Zdroj: pixino.com

Matice chápejme jako zobrazení, které má na vstupu vektor a na výstupu opět vektor. Vstupem bývá většinou podnět, kde rozhodující je nejenom síla podnětu, ale i jeho směr. Například nerovnováha tlaku. Výstupem bývá odezva, například proudění vyvolané nerovnováhou tlaku. Tato odezva v izotropním prostředí má směr podnětu, v prostředí s určitou strukturou by se však směr odezvy mohl odchýlit.

Užitečnost maticového součinu v materiálovém inženýrství si můžeme znázornit na proudění vody po povrchu země. Voda teče z kopce dolů, tento směr však můžeme ovlivnit vyoráním brázd. Hnací síla je gravitace, která směřuje z kopce dolů. Odezvou na gravitaci je tok vody, který směřuje velkou rychlostí dolů, pokud je pooráno po spádnici, malou rychlostí dolů, pokud je pooráno po vrstevnici a pokud je pooráno našikmo, tak něco mezi směrem dolů a směrem brázdy. V materiálu se může odehrávat totéž.

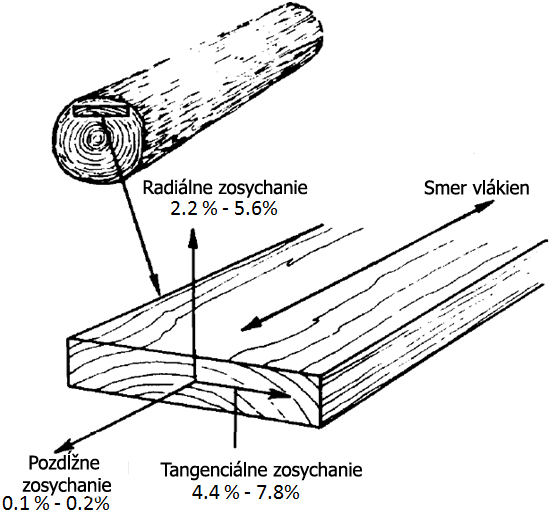
Výše popsané chování pozorujeme i u proudění podzemní vody, kde hnací silou kromě hladiny podzemní vody může být tlak, nebo u proudění vody ve dřevě, kde hnací silou definující pojem “z kopce dolů” je nerovnoměrnost v rozložení koncentrace vody ve dřevě (jedna část dřeva má větší vlhkost než jiná část) nebo nerovnoměrnost v teplotě (termodifuze, Sorettův efekt, transport vlhkosti vyvolaný rozdílem teplot). Výsledné proudění však nemusí přesně sledovat pokles koncentrace vlhkosti. Například dřevo vede podélně vlhkost zpravidla více než desetkrát lépe než v jiných směrech a chová se tedy, jako by v něm byly brázdy odklánějící vodu do podélného směru.

Matematický prostředek, který umožňuje snadno vektoru změnit velikost nebo i směr je právě tenzor (matice) a maticový součin.

Poznámka (tenzor).

Pod pojmem tenzor si můžeme představit veličinu, která figuruje v nějakém fyzikálním zákoně spojujícím dvě vektorové veličiny (podnět a odezvu na podnět) a násobení tenzorem definuje vztah mezi nimi. Pokud jsou podnětem a odezvou vektory, které mají stejný směr, stačí toto násobení provést pomocí skalární veličiny. Pokud však směr vektoru udávajícího odezvu není stejný jako směr vektoru udávajícího podnět, je nutné použít postup, který si s jiným směrem vektoru na vstupu a na výstupu poradí. A tímto postupem je právě maticový součin. Zatímco tedy například tok tepla v izotropních materiálech můžeme studovat pomocí skalárních materiálových charakteristik, tok tepla v anizotropních materiálech už musíme popisovat pomocí tenzorových materiálových charakteristik. Proto například u vedení tepla ve dřevě udáváme součinitele vedení tepla $\lambda_L$, $\lambda_R$ a $\lambda_T$ pro každý anatomický směr samostatně a z těchto veličin poté sestavujeme tenzor tepelné vodivosti $$\begin{pmatrix}\lambda_L &0&0 \cr 0&\lambda_R&0\cr 0&0&\lambda_T\end{pmatrix}.$$

Vlastní čísla a vlastní vektory

https://youtu.be/-vYq_TzC6jo

U zobrazování vektorů pomocí maticového násobení nás velice zajímá, které směry se zachovávají, tj. kdy bude obrazem vektoru jeho násobek.

Definice (vlastní vektor a vlastní hodnota matice).

Řekneme, že nenulový vektor $\vec u$ je vlastním vektorem matice $A$ příslušným vlastní hodnotě $\lambda$, jestliže platí $$A \vec u=\lambda \vec u.$$

Vlastní čísla se nazývají též vlastní hodnoty matice. Každý nenulový vlastní násobek vlastního vektoru je vlastní vektor příslušný téže vlastní hodnotě.

Poznámka (vlastní vektory a materiálové inženýrství).

Vlastní vektory jsou nesmírně důležité, protože definují směry, podél nichž se zobrazení chová “pěkně”. Tímto zobrazením může být třeba to, jak se působení vnější síly na těleso projeví na deformaci tohoto tělesa nebo jak se gradient teploty nebo vlhkosti projeví na proudění tepla či vody ve dřevě, půdě nebo jiném materiálu. Často se v aplikacích maticové zobrazení objevuje v konstitučních vztazích, vztazích mezi podnětem a materiálovou odezvou. Vlastní směry jsou tedy směry, ve kterých má odezva stejný směr jako podnět.

Pro pravidelně rostlé dřevo je snadné tyto směry určit, jsou to anatomické směry dřeva. Pro zkroucené dřevo nebo při studiu proudění vody, vzduchu či ropy v půdě to již tak snadné není a je nutné tyto směry vypočítat. To se naučíme později.

Dřevo není izotropní materiál a nemá stejné vlastnosti v každém směru. Existují ale tři výrazné směry, vzhledem k nimž se dají mechanické a fyzikální vlastnosti popsat snadněji, než vhledem ke směrům ostatním. Matematicky se jedná o vlastní vektory příslušných maticových fyzikálních veličin. Zdroj: http://woodpoint.sk

manim:Eigenvectors|vfzT25D6Zz8|Vlastní směry z hlediska materiálového inženýrství pro ortotropní materiály.

Příklad. Matice rotace nemá žádnou vlastní hodnotu (pokud tedy uvažujeme vlastní hodnoty v množině reálných čísel), protože pootočením se změní směr všech vektorů. Vlastní hodnoty existují pouze pro otočení o násobky $180^\circ$.

Příklad. Matice $\begin{pmatrix} 3 & 0\\ 0 & 3 \end{pmatrix}$ (trojnásobek jednotkové matice) zobrazuje každý vektor na trojnásobek a všechny vektory jsou vlastními vektory této matice. Příslušná vlastní hodnota je $3$.

Příklad. Matice $\begin{pmatrix} 3 & 0\\ 0 & 0 \end{pmatrix}$ má vlastní vektor $(1,0)$ příslušný vlastní hodnotě $3$ a vlastní vektor $(0,1)$ příslušný vlastní hodnotě $0$. Protože vlastními vektory jsou i nenulové násobky, je vlastním vektorem každý nenulový vektor, který má nulovou druhou komponentu (vlastní hodnota je $3$) nebo první komponentu (vlastní hodnota je $0$).

Příklad. Platí $\begin{pmatrix} 3 & -2\\ -1 & 4 \end{pmatrix} \begin{pmatrix} 2\\1 \end{pmatrix} = \begin{pmatrix} 4\\2 \end{pmatrix}$ a matice $\begin{pmatrix} 3 & -2\\ -1 & 4 \end{pmatrix}$ má vlastní vektor $(2,1)$ příslušný vlastní hodnotě $2$, protože vektor $(4,2)$ je dvojnásobkem vektoru $(2,1)$. Vlastním vektorem je i každý nenulový násobek vektoru $(2,1)$.

Zda umíte použít součin matice a vektoru k ověření toho, zda je vektor vlastním vektorem a k nalezení vlastního čísla si můžete vyzkoušet online.

ww2:problems/vlastni_cisla/01.pg

ww2:problems/vlastni_cisla/02.pg

manimp:PumpkinTransform|Popis transformace je jednodušší, pokud jsou osy současně i vlastními směry této transformace.

Příklad. Stacionární stav Markovova řetězce je vlastním vektorem matice, která tento řetězec reprezentuje. Příslušná vlastní hodnota je $1$. To plyne hned z rovnosti $$M\vec q=\vec q.$$ Kromě toho mohou existovat i další vlastní hodnoty, z praktického hlediska méně zajímavé.

Příklad. Vlastní hodnoty a vektory jsou jedním z hlavních stavebních kamenů algoritmu, kterým Google provádí hodnocení důležitosti webových stránek. Vlastní vektory se počítají iteračně, odpovídá to vlastně modelu, kdy Markovův řetězec začneme v libovolném výchozím stavu a postupným iterováním se dostaneme do stacionárního stavu reprezentovaného vlastním vektorem.

Příklad. Leslieho matice má jednu kladnou vlastní hodnotu. Příslušný vlastní vektor definuje rozložení četnosti zastoupení jednotlivých věkových kategorií u populace ve stacionárním stavu. (Toto není tvrzení patrné na první pohled, ale dá se dokázat.)

V aplikacích často bývá matice “symetrická podle diagonály” a u takové matice vlastní vektory vždy existují. Co se přesně myslí pod pojmem “symetrická matice” si uvedeme na následujícím slidu.

Transponovaná matice

https://youtu.be/Toqwz-Oxg-4

Definice (transponovaná matice).

Buď $A=(a_{ij})\in\mathbb R^{m\times n}$ matice. Matice, která vznikne záměnou řádků matice $A$ za sloupce se nazývá matice transponovaná k matici $A$. Matici transponovanou označujeme symbolem $A^T$. Platí tedy $A^T\in\mathbb R^{n\times m}$ a $$A^T=(a_{ji}),$$ kde $a_{ij}$ jsou prvky matice $A$.

Příklad. Matice transponovaná k matici $A= \begin{pmatrix} 1& -2& 3\\ 0& 1 &3\\ 2& 1 &9 \end{pmatrix}$ je $A^T=\begin{pmatrix} 1& 0 &2 \\ -2& 1& 1\\ 3 &3 &9 \end{pmatrix}.$

Příklad. Skalární součin sloupcových vektorů (chápaných jako matice) $u= \begin{pmatrix} 1\\-2\\ a \end{pmatrix}$ a $v= \begin{pmatrix} 2\\-4\\ 1 \end{pmatrix}$ je možno zapsat jako maticový součin $$u^T v= \begin{pmatrix} 1& -2 & a \end{pmatrix} \begin{pmatrix} 2\\-4\\ 1 \end{pmatrix} =(a+10).$$

Příklad. Matice, která se nemění transponováním, tj. $a_{ij}=a_{ji}$ se nazývá symetrická. Matice, která splňuje $a_{ij}=-a_{ji}$ se nazývá antisymetrická. Pro libovolnou čtvercovou matici $A$ platí $$A=\frac{A+A^T}2+\frac{A-A^T}2.$$ První matice v tomto součtu je symetrická a druhá antisymetrická. Takto je možné rozložit matici na součet symetrické a antisymetrické matice. Například matice $$A= \begin{pmatrix} -4 & 7 \\ -1 & 2 \end{pmatrix}$$ má tento rozklad ve tvaru $$A= \begin{pmatrix} -4 & 3 \\ 3 & 2 \end{pmatrix} + \begin{pmatrix} 0 & 4 \\ -4 & 0 \end{pmatrix}.$$ Tento trik použijeme pro odvození tvaru tenzoru malých deformací, ze zobrazení takto totiž dokážeme odfiltrovat část související s pootočením a část, která s pootočením nesouvisí. Ta druhá nás zajímá, protože popisuje deformaci.

Věta (souvislost transponování matice a maticového součinu).

Pro čtvercové matice platí $$(AB)^T=B^T A^T.$$

Příklad. Pro Markovův řetězec s maticí a sloupcovými vektory $\vec q$ dostaneme transponováním vztahu $$\vec q_{k+1}=A\vec q_k$$ vztah $$\vec q^T_{k+1}=\vec q^T_k A^T$$ s řádkovými vektory a maticí, která má součet čísel v každém řádku roven 1. Takto jsou Markovovy řetězce také často zaváděny, například na Wikipedii.

Tenzor malých deformací

https://youtu.be/5AMXMQyx3jw

Metodami lineární algebry kombinovanými s diferenciálním počtem dokážeme ve zobrazení identifikovat tenzor malých deformací, složku související jenom se změnou tvaru. Odfiltrujeme tak posun či rotaci, které se změnou tvaru nesouvisí. Zdroj: pixabay.com

Zobrazení roviny do sebe, které může odpovídat deformaci tělesa působením síly, je možné popsat dvojicí funkcí $u_1(x_1,x_2)$, $u_2(x_1,x_2)$. Lineární aproximace těchto funkcí v okolí bodu $(x_1,x_2)$ dávají (viz závěr prezentace z přednášky věnované derivací, kdy ještě vpravo pro stručnost vynecháváme argument $(x_1,x_2)$) $$\begin{aligned} u_{1}(x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2})&\approx u_{1}+\frac{\partial u_{1}}{\partial x_{1}}\Delta x_{1}+\frac{\partial u_{1}}{\partial x_{2}}\Delta x_{2},\\ u_{2}(x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2})&\approx u_{2}+\frac{\partial u_{2}}{\partial x_{1}}\Delta x_{1}+\frac{\partial u_{2}}{\partial x_{2}}\Delta x_{2}, \end{aligned}$$ což je možné zapsat maticově jako $$\begin{pmatrix} u_1 (x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2}) \\ u_2 (x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2}) \end{pmatrix} \approx \begin{pmatrix} u_1\\u_2 \end{pmatrix}+ \begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac{\partial u_{1}}{\partial x_{2}}\\ \frac{\partial u_{2}}{\partial x_{1}} & \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} \begin{pmatrix} \Delta x_1 \\ \Delta x_2 \end{pmatrix}.$$ Člen $\begin{pmatrix} u_1\\u_2 \end{pmatrix}$ je posunutí, proto nás zajímá až druhý člen, obsahující deformaci. Pokud matici $$D= \begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac{\partial u_{1}}{\partial x_{2}}\\ \frac{\partial u_{2}}{\partial x_{1}} & \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix}$$ rozdělíme stejným obratem jako na předešlém slidu na součet symetrické a antisymetrické matice, dostaneme $$D= \overbrace{\begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)\\ \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)& \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} }^{D_{\text{sym}}} + \underbrace{ \begin{pmatrix} 0 & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)\\ - \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)& 0 \end{pmatrix}}_{D_{\text{asym}}}.$$ Druhá část reprezentuje pootočení, což snadno nahlédneme, pokud tuto informaci sečteme s identitou reprezentovanou jednotkovou maticí na $$D_{\text{asym}}+I=\begin{pmatrix} 1 & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)\\ - \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)& 1 \end{pmatrix}$$ abychom měli celou část zobrazení (ne jenom deformaci). Porovnáním s maticí malých rotací $$R_{\theta,0}= \begin{pmatrix} 1 & - \theta\\ \theta & 1 \end{pmatrix}$$ odvozenou na jednom z předchozích slidů získáme přímo pootočení. V teorii deformace nás zajímá spíše symetrická část, tj. matice $$D_{\text{sym}}=\begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)\\ \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)& \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix}$$ popisující změnu tvaru a nazývaná tenzor malých deformací. Ten se ještě někdy rozděluje na součet vhodného konstantního násobku jednotkové matice (souvisí se zvětšením nebo zmenšením, tj. se změnou objemu) a deviátor (souvisí se zmenou tvaru bez započtení zvětšení či zmenšení).

Pro využití v dřevařských úlohách viz též A. Požgaj, Štruktúra a vlastnosti dreva str 318 nebo P. Horáček, Fyzikální a mechanické vlastnosti dřeva I, str. 40. Analogicky, ale pro rychlosti, je definován tenzor rychlosti přetvoření (deformační rychlost) používaný v hydrodynamice. Můžeme ji dostat jako derivaci tenzoru malých deformací (při studiu deformací), nebo jako symetrickou část matice vytvořené gradienty jednotlivých komponent rychlosti proudění. Pro proudění vody viz J. Říha, Matematické modelování hydrodynamických a disperzních jevů, kap. 3.3.

Obrázky a online výpočty, Sage.

Rozložení teploty na tepelně vodivé desce

https://youtu.be/xV46lYgdHSQ

Na závěr si ukážeme, že pomocí lineární algebry a maticového počtu je možno popsat funkci dvou proměnných popisující rozložení teploty na tepelně vodivé desce. Postup je takový, že budeme sledovat teplotu v referenčních bodech. Požadavek, že teploty v okolních bodech mají odpovídat našim představám o vedení tepla vyjádříme kvantitativně pomocí vhodné matice.

Rozložení teploty na tepelně vodivé desce je možné přibližně zkoumat metodami lineární algebry. A až na některé triviální případy jinou možnost vlastně nemáme, protože přesné řešení rovnice vedení tepla je v prakticky zajímavých případech nereálné. Podobně to je s mechanickým namáháním nebo transportem látek porézním prostředím.

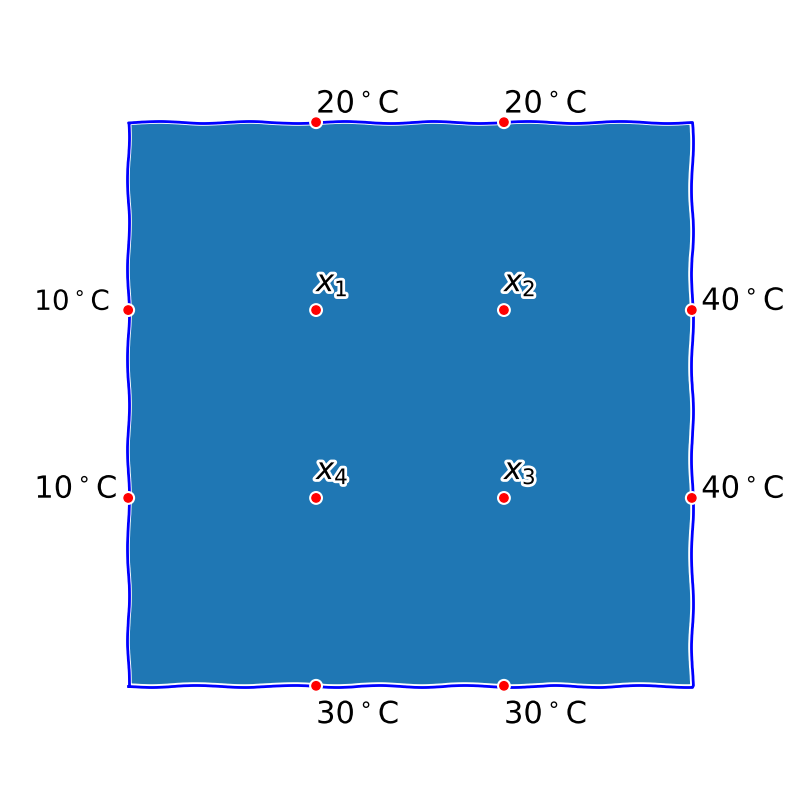
Uvažujme čtvercovou desku, kterou si rozdělíme sítí na $12$ uzlových bodů (rohy zanedbáme) jak je uvedeno na obrázku. V uzlových bodech na okraji desky je teplota zadána (okrajová podmínka), zajímá nás rozložení teploty v ostatních uzlových bodech.

Učiníme (poměrně realistický) předpoklad, že teplota v každém uzlovém bodě je díky tepelné vodivosti desky ovlivněna sousedními uzlovými body. Každý sousední bod má stejný vliv, proto teplota v uzlovém bodě bude přibližně rovna aritmetickému průměru teplot v sousedních bodech. Kvantitativně zformulováno, platí $$\begin{aligned} x_1&=\frac 14(10+20+x_2+x_4)\\ x_2&=\frac 14(20+40+x_1+x_3)\\ x_3&=\frac 14(30+40+x_2+x_4)\\ x_4&=\frac 14(10+30+x_1+x_3) \end{aligned}\tag{1}$$ anebo po úpravě $$\begin{aligned} 4x_1-x_2-\qquad x_4&=30\\ -x_1+4x_2-x_3\qquad&=60\\ \qquad-x_2+4x_3-x_4&=70\\ -x_1\qquad-x_3+4x_4&=40 \end{aligned}$$ Dostali jsme soustavu lineárních rovnic o čtyřech neznámých. Tuto úlohu je možno zformulovat pomocí lineární kombinace $$\begin{pmatrix} 4\\-1\\0\\-1 \end{pmatrix} x_1 + \begin{pmatrix} -1\\4\\-1\\0 \end{pmatrix} x_2 + \begin{pmatrix} 0\\-1\\4\\-1 \end{pmatrix} x_3 + \begin{pmatrix} -1\\0\\-1\\4 \end{pmatrix} x_4 = \begin{pmatrix} 30\\60\\70\\40 \end{pmatrix}$$ nebo pomocí maticového násobení (s vynechanými nulami uvnitř matice) $$\begin{pmatrix} \phantom{-}4&-1&&-1\\ -1& \phantom{-}4&-1&\\ &-1& \phantom{-}4&-1\\ -1&&-1& \phantom{-}4 \end{pmatrix} \begin{pmatrix} x_1\\x_2\\x_3\\x_4 \end{pmatrix} = \begin{pmatrix} 30\\60\\70\\40 \end{pmatrix}.$$ Úloha je tedy převoditelná na úlohu řešení soustavy lineárních rovnic. Pro podrobnější popis použijeme stejnou myšlenku, ale mnohem více uzlových bodů. Postup je stejný, pouze vznikne soustava s více neznámými a více rovnicemi.

Poznámka. Rovnice popisující vedení tepla na základě fyzikálních principů je poměrně komplikovaně řešitelná a proto se zpravidla převádí na problém lineární algebry. Může to znít překvapivě, ale skončíme u něčeho podobného jako v našem jednoduchoučkém modelu. Výše uvedený postup se nazývá metoda konečných diferencí, ale jsou i další metody, například metoda konečných prvků. Společným znakem je rozdělení oblasti našeho zájmu na velké množství bodů a aproximace fyzikálních zákonů pro sledovaný jev v každém bodě pomocí lineární rovnice. Tím vznikne úloha na řešení soustavy rovnic. Používá se k modelování proudění tepla nebo vody, k modelování mechanického namáhání od jednoduchých nosníků po komplikované konstrukce nebo stromy. Soustava vytvořená pomocí takových modelů je velmi řídká, má hodně nul. Je proto možné ji rychle vyřešit i v případě tisíců rovnic. My se později například naučíme chytře využít toho, že každý řádek má v hlavní diagonále větší číslo, než je součet zbylých čísel v tomto řádku.

Poznámka (iterační metoda).

Soustavu (1) je možno vyřešit iterační metodou. Je možno postupovat intuitivně. Vyjdeme z libovolného odhadu řešení a teplotu v každém bodě budeme opakovaně nahrazovat průměrem teplot v okolních bodech, dokud se hodnoty neustálí. Kdy tento postup funguje a jak se dá zformalizovat si ukážeme později (Jacobiho metoda).

Online výpočet maticově.

Online výpočet rovnicemi.

Shrnutí, hlavní myšlenky

A jaká je hlavní message? Zdroj: pixabay.com

• Seznámili jsme se s vektory. S objekty, které umožňují pracovat s veličinami mající kromě numerické hodnoty i směr.
• Seznámili jsme se s maticemi, s objekty, které umožní pracovat se zobrazením vektorů na vektory, kdy směr vzoru a obrazu nemusí být (na rozdíl od násobení reálným číslem) stejný. Díky tomu dokážeme popsat reakci materiálu na podněty v případě, kdy má materiál v různých směrech různé vlastnosti.
• Matice umožňují kompaktní zápis soustavy libovolného počtu lineárních rovnic jedinou rovnicí $$AX=B.$$
• V materiálovém inženýrství pomocí matic (přesněji pomocí tenzorů) umíme popsat materiály, mající v různých směrech různé vlastnosti. V takových materiálech je různý směr vnějšího podnětu a odezvy na vnější podnět a bez matic jenom s použitím skalárních veličin není možné se závislostmi takového typu pracovat. Pokud chceme zobrazení, které mění směr vektorů (a má některé další rozumné vlastnosti), používáme matice. Přesněji, používáme tenzory, které mají v souřadnicích podobu matic.