| Způsob vyhodnocení: Při vyhodnocení budou započteny jen správné odpovědi. |
| Vypočtěte determinant
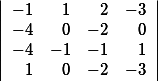
| |
|
| | Vypočtěte 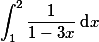
| |
|
| Objem rotačního tělesa, které vznikne rotací kolem osy x rovinného obrazce ohraničeného křivkami
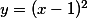 , , 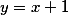 , se vypočte pomocí vztahu : , se vypočte pomocí vztahu :
| |
|
| | Kořen algebraické rovnice 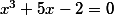
, určený s chybou menší než 0,08 ležící v intervalu (0,1) má hodnotu: | |
|
| | Lagrangeův polynom, procházející [2,1],[4,3],[6,-2] body má tvar : | |
|
| | Vypočtěte 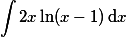
| |
|
| | Vypočtěte 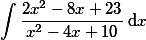
| |
|
| |