Způsob vyhodnocení: Při vyhodnocení budou započteny jen správné odpovědi.
1.

P(x) je polynom stupně n. Rovnice  P(x)=0 má v oboru R :
buď n kořenů nebo o sudý počet méně
právě n kořenů
tolik kořenů, kolik je znaménkových změn nebo o sudý počet méně
tolik kořenů, kolik je znaménkových změn v posloupnosti koeficientů polynomu

2.

Rovnice  x^3-2x^2+x-1=0

má 3 reálné kořeny, z toho 2 nebo žádný kladný, jeden záporný
má 4 kořeny, z toho 3 nebo 1 kladné, jeden záporný
má 3 reálné kořeny, z toho 3 nebo 1 kladné, jeden záporný
má 3 reálné kořeny, z toho 3 nebo 1 kladné, žádný záporný

3.

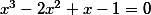Separujte všechny reálné kořeny rovnice

x^3+4x^2+x-5=0

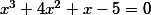
Vyberte správnou možnost intervalu(ů), kde tyto kořeny leží

(-4,-3),(-2,-1),(0,1)
(-6,5)
(0,1)
(4,5)

4.

Metodou půlení intervalu určete kořen rovnice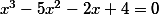

x^3-5x^2-2x+4=0

ležící v intervalu (0,1) s chybou menší než 0,1
0,1875
0,8125
0,5625
0,375