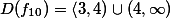1. Příklad
Určete definiční obor funkce 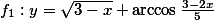
Řešení: 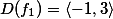
Určete definiční obor funkce 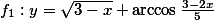
Řešení: 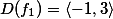
Určete definiční obor funkce 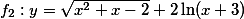
Řešení: 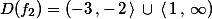
Určete definiční obor funkce 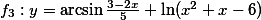
Řešení: 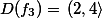
Určete definiční obor funkce 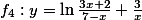
Řešení: 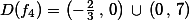
Určete definiční obor funkce 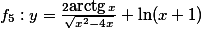
Řešení: 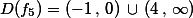
Určete definiční obor funkce 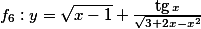
Řešení: 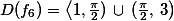
Určete definiční obor funkce 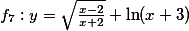
Řešení: 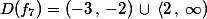
Určete definiční obor funkce 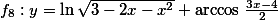
Řešení: 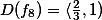
Určete definiční obor funkce ![Matematický text f_9:y=\arccos\,(\frac{2}{x+1})+\sqrt[3]{x+1}](../objects/vzorec17.png)
Řešení: 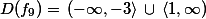
Určete definiční obor funkce 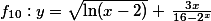
Řešení: