Derivace funkce více proměnných
Robert Mařík
2020
Pokud se matematické výrazy nezobrazují korektně, nechejte znovunačíst stránku (Reload, Crtl+R, F5) nebo použijte html verzi prezentace.
Ovládání: Prezentaci je možno posouvat šipkami nebo mezerníkem. Klávesa "S" zmenšuje písmo, "B" zvětšuje (smaller/bigger). Klávesa "C" zobrazí obsah (content). Klávesou "A" se přepíná režim prezentace/html stránka.
Kliknutím na obrázek se obrázek zvětší na vertikální rozměr okna. Pro zavření zvětšeniny klikněte do zašedlého zbytku stránky nebo použijte klávesu "ESC".
Slidy jsou doprovodným materiálem k předáškám. Některá tvrzení platí
pouze za předpokladů dostatečné spojitosti funkcí nebo jejich
derivací. V jednoduchých technických aplikacích bývají tyto
předpoklady splněny a proto je nezmiňujeme. Přesná formulace vět je
v učebním textu a v odborné literatuře.
Anotace.
- Naučíme se sledovat rychlost, s jakou se mění veličina, kterou sledujeme.
- U veličin, které mají více vstupních údajů, budeme sledovat samostatně reakci na změnu vždy u jediného vstupního údaje. Například u teploty budeme sledovat buď jak se v daném místě mění teplota v čase, nebo jak se v daný okamžik mění teplota s polohou.
- Aparát využijeme k tomu, že z fyzikálních zákonů sestavíme rovnici vedení tepla. To bude matematický model umožňující jednak modelování přenosu tepla a jednak kontrolu toho, že fyzikální zákony vedoucí k formulaci této rovnice jsou správné.
Prerekvizity.
- Navážeme na znalosti z diferenciálního počtu funkcí jedné proměnných. Zejména definice, využití a výpočet derivace.
- Zopakujte si fyzikální (praktický) význam derivace a pro osahání si konkrétních příkladů také základní metody výpočtu.
Funkce jedné proměnné
- Zobrazení \(f: \mathbb{R}\to \mathbb{R}\) se nazývá funkce jedné proměnné.
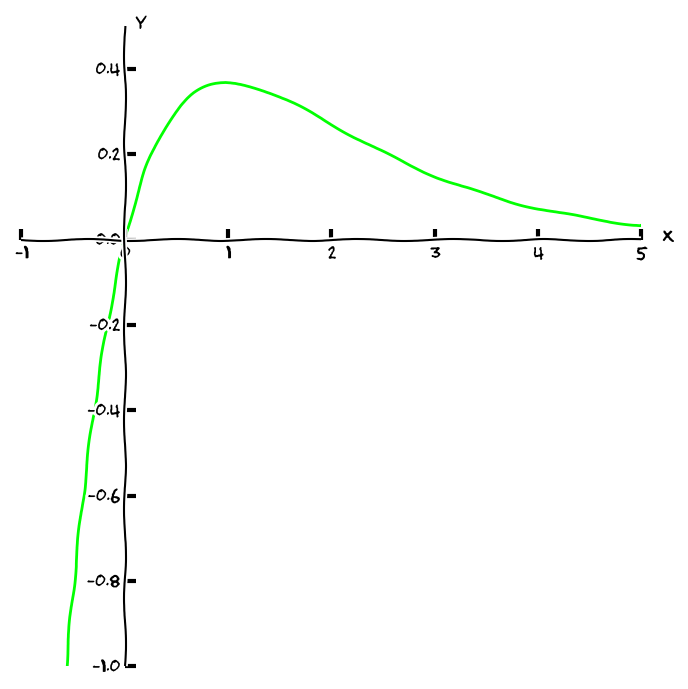
- V kartézské rovině píšeme též \(y=f(x)\), kreslíme uspořádané dvojice bodů \([x,y]\) a výstupem je zpravidla křivka v rovině (Nakreslit online.)
- Rychlost změny je derivace: \[f'(x):=\lim_{h\to 0}\frac{f(x+h)-f(x)}h\]
- Podle kontextu a oborových zvyklostí zapisujeme derivaci pomocí čárky (někdy tečky) nebo jako podíl diferenciálů \[y', \quad \frac{\mathrm dy}{\mathrm dx}, \quad \frac{\mathrm d}{\mathrm dx}y\]
- rychlost změny změny je druhá derivace: \[y'',\quad \frac{\mathrm d^2y}{\mathrm dx^2}, \quad\frac{\mathrm d^2}{\mathrm dx^2}y\]
Poznámka (Newtonův zákon tepelné výměny).
Je-li \(T(t)\) teplota tělesa v čase \(t\), je \(\frac{\mathrm dT}{\mathrm dt}\) změna této teploty za jednotku času, tj. rychlost s jakou roste teplota. Častým modelem reálné situace je předpoklad, že tato teplota je úměrná rozdílu teploty tělesa a teploty okolí. Pokud je teplota okolí konstantní a rovna \(T_0\), dostáváme takto modely \[\frac{\mathrm dT}{\mathrm dt}= k(T_0-T)\] pro ohřev (teplota okolí je vyšší a teplota tělesa roste) a \[\frac{\mathrm dT}{\mathrm dt}= -k(T-T_0)\] pro ochlazování (teplota okolí je nižší, těleso se ochlazuje a má zápornou derivaci podle času).
Poznámka (lineární aproximace, materiálové vztahy).
Změna \(\Delta x\) v proměnné \(x\) vyvolá změnu \(\Delta y\approx f'(x) \Delta x\). Proto je možné používat lineární aproximaci funkce \[f(x)\approx f(x_0)+f'(x_0)(x-x_0). \] Například naprostá většina materiálových vztahů je takovou aproximací pro \(x_0=0\) (relativně malé podněty) a \(f(x_0)=0\) (bez podnětu není odezva). Lineární aproximace má poté tvar \[f(x)\approx f'(0)x=kx.\] Proto jsou zákony jako Fourierův, Fickův nebo Darcyho formulovány ve tvaru přímé úměrnosti. S těmito zákony jste se pravděpodobně seznámili v naukách o materiálu, blíže se jim budeme věnovat později. Podobně je možno chápat Newtonův zákon tepelné výměny jako lineární aproximaci případného složitějšího vztahu.
Poznámka (logistický růst populace).
Je-li \(x(t)\) velikost populace živočichů, je \(\frac{\mathrm dx}{\mathrm dt}\) změna této velikosti za jednotku času. Častým modelem reálné situace je modelování pomocí logistické rovnice \[\frac{\mathrm dx}{\mathrm dt}=r x (K-x)\] kdy předpokládáme, že rychlost růstu je úměrná velikosti populace a volné kapacitě prostředí. Konstanta \(K\) je celková kapacita prostředí.
Poznámka (pohybová rovnice).
Při pohybu po přímce je \(x=f(t)\) poloha v čase \(t\), rychlost je \(\frac{\mathrm dx}{\mathrm dt}\) a zrychlení je \(\frac{\mathrm d^2x}{\mathrm dt^2}\). Podle Newtonova pohybového zákona platí \[m\frac{\mathrm d^2x}{\mathrm dt^2} =F,\] kde \(F\) je výsledná síla působící na objekt.
Funkce dvou proměnných, graf
- Zobrazení \(f: \mathbb{R}^2\to \mathbb{R}\) se nazývá funkce dvou proměnných.
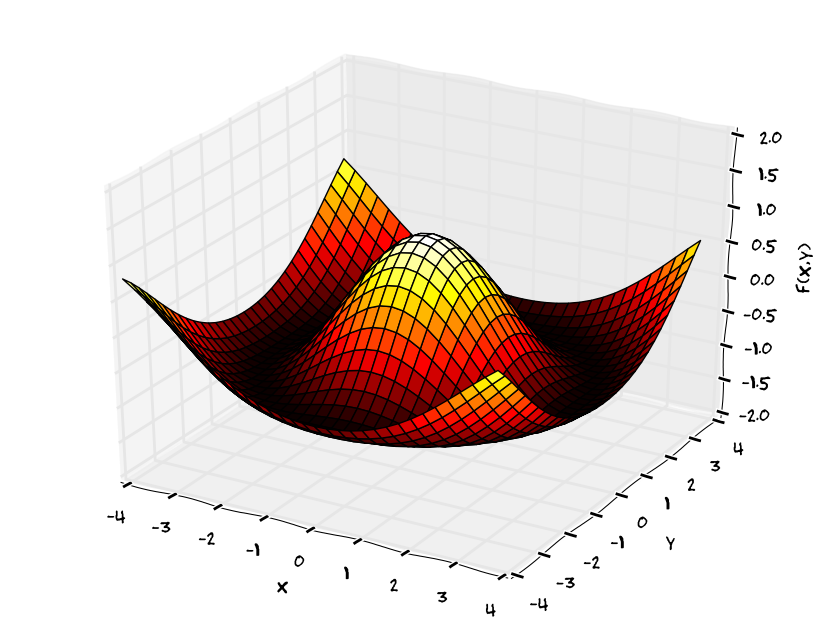
- Grafem funkce \(f\) je množina uspořádaných trojic \([x,y,z]\), které splňují \(z=f(x,y)\) . Graf kreslíme zpravidla jako body v 3D prostoru.
Příkladem skalární funkce dvou prostorových proměnných je teplota v určitém okamžiku na dvourozměrném povrchu. Aparát funkcí dvou proměnných se tedy jistě uplatní při studiu tepelných ostrovů souvisejících s urbanizací a kvalitou života ve městech.
Příkladem skalární funkce dvou proměnných, kdy každá z proměnných má jiný charakter, je teplota ve stěně budovy. Tato teplota se mění s časem (studená stěna, na kterou začalo svítit slunce, se ohřívá) a s polohou (vnější a vnitřní okraj stěny mají teplotu přibližně podle teploty venku a teploty uvnitř budovy, uvnitř stěny se teplota spojitě mění).
Parciální derivace
Pokud sledujeme například ve stěně měnící se teplotní profil, zajímá nás, jak se teplota v jednotlivých místech stěny mění v čase a jak se teplota mění v řezu stěnou. Zdá se býti rozumné oddělit obě změny. Buď v daném bodě fixovat polohu a sledovat časový vývoj v tomto bodě, nebo v daném čase udělat něco jako teplotní snímek a srovnávat teplotu ve vybraném bodě s okolními teplotami ve stejném čase. To vede k následujícímu přístupu, kdy u funkce více proměnných sledujeme reakci na změnu jedné jediné veličiny.
Definice (parciální derivace).
Buď \(f\colon \mathbb R^2\to\mathbb R\) funkce dvou proměnných, \(x\) a \(y\), tj. \(f(x,y)\). Výraz \[\frac{\partial f}{\partial x}:=\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}h\] se nazývá parciální derivace funkce \(f\) podle \(x\). Podobně, \[\frac{\partial f}{\partial y}:=\lim_{h\to 0}\frac{f(x,y+h)-f(x,y)}h\] je parciální derivace funkce \(f\) podle \(y\).
Podobně můžeme definovat parciální derivaci pro funkce libovolného konečného počtu proměnných. V těchto parciálních derivacích vlastně sledujeme, jak reaguje veličina \(f\) na změny jenom v jedné proměnné. Proměnná, přes kterou se nederivuje, má vlastně roli parametru a nijak se nemění.
Poznámka (rozšifrování definice derivace).
- Výraz z čitatele, tj. \(f(x+h,y)-f(x,y)\), je změna veličiny \(f\) na intervalu \([x,x+h]\) při konstantní veličině \(y\). Často označujeme též \(\Delta f\).
- Podíl, tj. \(\frac{f(x+h,y)-f(x,y)}h\) je změna veličiny \(f\) na intervalu \([x,x+h]\) při konstantní veličině \(y\), přičemž tato změna je přepočítaná na jednotku veličiny \(x\), tj. v jistém smyslu průměrná rychlost změny vzhledem k \(x\) na intervalu \([x,x+h]\). Často označujeme též \(\frac{\Delta f}{\Delta x}\).
- Limita v definici derivace stahuje délku intervalu, na kterém počítáme průměrnou rychlost, k nule. Tím se z průměrné rychlosti stane okamžitá rychlost. Parciální derivace je tedy okamžitá rychlost s jakou se mění funkce \(f\) při změnách jedné proměnné.
Jednotka derivace \(\frac{\partial f}{\partial x}\) je stejná, jako jednotka podílu \(\frac {f}x\). Jednotka derivace \(\frac{\partial f}{\partial y}\) je stejná, jako jednotka podílu \(\frac {f}y\).
Derivace \(\frac{\partial f}{\partial x}\) udává, jak se mění veličina \(f\) při změnách veličiny \(x\) a předpokladu konstantní veličiny \(y\). Interpretace derivace v nematematických disciplínách je okamžitá rychlost s jakou veličina \(f\) reaguje na změny veličiny \(x\).
Pokud sledujeme vývoj a rozložení teploty na dvourozměrné tepelně vodivé desce, je teplota (udávaná například ve stupních Celsia) funkcí tří proměnných: jedna proměnná je čas \(t\) a dvě proměnné \(x\) a \(y\) jsou souřadnice v rovině. Tedy \(T=T(t,x,y).\) Parciální derivace \(\frac{\partial T}{\partial t}\) udává je rychle (například ve stupních Celsia za hodinu) roste v daném místě teplota. V různých částech desky může být tato veličina jiná a vždy se vztahuje k danému bodu. Může se měnit i v čase, například deska v prostředí s konstantní teplotou postupně dospěje do stavu se stacionárním rozložením teploty, kdy se teplota v žádném místě ani neroste ani neklesá a parciální derivace podle času je nulová. Derivace \(\frac{\partial T}{\partial x}\) udává jak prudce (například ve stupních Celsia na centimetr) roste teplota ve směru osy \(x\).
Interpretace parciálních derivací - brzdná dráha
Příklad: Brzdná dráha \(L\) (v metrech) auta o hmotnosti \(m\) (v kilogramech) brzdícího z rychlosti \(v\) (v kilometrech za hodinu) je dána vzorcem \[L=k m v^2, \] kde \(k= 3.45 \times 10 ^{-6}\,(\mathrm{m}\,\mathrm{hod}^2)/(\mathrm{kg}\,\mathrm{km}^2)\). Pro \(m=1100\,\mathrm{kg}\) a \(v=100\,\mathrm{km}/\mathrm{hod}\) je brzdná dráha \(37.95\,\mathrm{m}\).
- Parciální derivace podle \(m\) je \(\frac{\partial L}{\partial m}=kv^2\) a pro zadané hodnoty vychází \[\frac{\partial L}{\partial m}=0.0345 \mathrm{m}/\mathrm{kg}.\] Každý kilogram hmotnosti nad \(1100\,\mathrm{kg}\) auta jedoucího rychlostí \(100\,\mathrm{km}/\mathrm{hod}\) prodlouží brzdnou dráhu o cca \(3.5\,\mathrm{cm}\).
- Parciální derivace podle \(v\) je \(\frac{\partial L}{\partial v}=2kmv\) a pro zadané hodnoty vychází \[\frac{\partial L}{\partial v}=0.759\,\mathrm{m}/(\mathrm{km}/\mathrm{hod})=7.59\times 10^{-4}\,\mathrm{hod}.\] Každý kilometr za hodinu nad \(100\,\mathrm{km}/\mathrm{hod}\) u auta vážícího \(1100\,\mathrm{kg}\) prodlouží brzdnou dráhu o cca \(76\,\mathrm{cm}\).
- Zjednodušený vzorec pro brzdnou dráhu auta s hmotností blízkou \(1100\,\mathrm{kg}\) a rychlostí blízkou \(100\,\mathrm{km}/\mathrm{hod}\) je \[L\approx 37.95+0.0345(m-1100)+0.759(v-100),\] kde hmotnost a rychlost se dosazují v kilogramech a kilometrech za hodinu a brzdná dráha vychází v metrech.
Online výpočet.
Interpretace parciálních derivací - pohyb ještěrky
Energie \(E\) (v kcal), kterou spotřebuje ještěrka o hmotnosti \(m\) (v gramech) na překonání vzdálenosti jednoho kilometru rychlostí \(v\) (v kilometrech za hodinu) se dá odhadnout vzorcem \[E(m,v)=2.65 m^{0.66} + \frac{3.5 m^{0.75}}{v}.\] Přímým výpočtem je možné určit \[\frac{\partial E}{\partial v}=-\frac{3.5 m^{0.75}}{v^2}.\] Pro \(m=400\,\mathrm{g}\) a \(v=8\,\mathrm{km}\,\mathrm{h}^{-1}\) dostáváme \[\frac{\partial E}{\partial v}(400,8)=-4.9\,\mathrm{kcal}\,\mathrm{km}^{-1}\mathrm{h}.\] Zvýšení rychlosti o kilometr za hodinu vede ke snížení energetického výdeje ještěrky o \(4.9\,\mathrm{kcal}\). Podobně, platí \[\frac{\partial E}{\partial m}={2.65}\times 0.66 {m^{-0.34}} + \frac{3.5\times 0.75 m^{-0.25}}{v}= \frac{1.749}{m^{0.34}} + \frac{2.625}{m^{0.25} v} \] a pro výše uvažované hodnoty dostáváme \[\frac{\partial E}{\partial m}(400,8)=
0.30\,\mathrm{kcal}\,\mathrm{g}^{-1}.
\] Každý gram, který má ještěrka navíc oproti hmotnosti \(400\) gramů, zvedne energetický výdej přibližně o \(0.30\,\mathrm{kcal}\).
Online výpočet.
(Zpracováno podle Stewart: Biocalculus)
Linearita parciální derivace
Následující poznámka je nenápadná a přirozená, protože je analogií stejného tvrzení pro obyčejné derivace. Má však mimořádnou důležitost, protože udává vlastnost, které se můžeme držet při studiu rovnic obsahujících derivace. Stejné věty zformulujeme i u dalších operací s funkcemi a později se je naučíme využívat.
Poznámka (linearita parciální derivace).
Parciální derivace zachovává součet a násobení konstantou, tj. pro libovolné funkce \(f\) a \(g\) a konstantu \(c\) platí \[\frac{\partial (f+g)}{\partial x}=\frac{\partial f}{\partial x}+\frac{\partial g}{\partial x}, \qquad \frac{\partial (cf)}{\partial x}=c\frac{\partial f}{\partial x}\] a analogicky pro libovolnou jinou proměnnou.
Rovnice vedení tepla v 1D
Studujme vedení tepla v jednorozměrné tyči. Teplota je funkcí dvou proměnných, polohy a času. Tedy \(T=T(t,x).\) Parciální derivace \(\frac{\partial T}{\partial t}\) udává je rychle (například ve stupních Celsia za hodinu) roste v daném místě teplota. V různých částech desky může být tato veličina jiná a vždy se vztahuje k danému bodu. Přirozeně se mění i v čase, například v prostředí s konstantní teplotou postupně systém dospěje do stavu se stacionárním rozložením teploty, kdy se teplota v žádném místě ani neroste ani neklesá a parciální derivace podle času je nulová. Derivace \(\frac{\partial T}{\partial x}\) udává jak prudce (například ve stupních Celsia na centimetr) roste teplota ve směru osy \(x\).
Poznámka.
Potřebujeme fyzikální zákony řídící vedení tepla. Bez nich matematika model vedení tepla nemá jak naformulovat. Tyto zákony je potřeba matematice dodat “z venku”, z aplikované vědy. Tou je v tomto případě fyzika, jindy může být biologie nebo geologie. Jakmile jsou potřebné zákony a případně materiálové vztahy k dispozici, stavé se problém čistě matematickým a fyzika přijde ke slovu při závěrečné interpretaci. Použijeme následující fyzikální fakta.
- Rozdílem teplot je způsoben tok tepla. Velikost toku tepla je úměrná teplotnímu rozdílu a teplo teče z místa v větší teplotou do místa s menší teplotou.
- Teplota se zvyšuje dodáním tepla. Změna teploty je úměrná dodanému teplu.
V dalším už nastupuje matematický popis a ve vhodných chvílích vždy použijeme výše uvedené fyzikální zákony. Mluvíme o teple, ale jako mechanický model si můžeme představit proudění tekutiny (pro jednoduchou představu) nebo proudění vlhkosti (pro odvození rovnice difuze namísto rovnice vedení tepla). Budeme uvažovat libovolné místo materiálu a budeme matematicky vyjadřovat děje, které přispívají ke změně teploty.
- Rychlost s jakou s daném místě roste teplota (v čase) je \[\frac{\partial T}{\partial t}\] a měříme ji například ve stupních Celsia za minutu. Tato rychlost je úměrná rychlosti s jakou do daného místa dodáváme teplo. Proto v dalším budeme hledat rychlost dodávání tepla a daného místa a poté se sem vrátíme a dáme tuto rychlost do souvislosti s rychlostí růstu teploty.
- Rychlost s jakou s daném místě roste teplota jako funkce polohy je \(\frac{\partial T}{\partial x}\) a měříme ji například ve stupních Celsia na centimetr. Tato rychlost musíme vzít záporně, abychom dostali pokles teploty a vynásobit konstantou, která převede spád teploty na tok tepla. Tuto konstantu označíme \(k\) (nazývá se součinitel teplné vodivosti a dodá nám ji fyzika, přesněji Fourierův zákon) a tok tepla \(q\) ve směru osy \(x\) je \[q=-k\frac{\partial T}{\partial x}.\] To je veličina, která udává, kolik joulů tepla proteče průřezem za jednotku času.
- Pokud do daného místa přitéká teplo stejnou rychlostí jako odtéká, teplota se nemění a dané místo se ani neohřívá ani neochlazuje. Intenzita ochazování je dána bilancí mezi přítokem a odtokem. Můžeme si to představit tak, že z tepla které do daného bodu přiteče, se část “oddělí” a přispěje k navýšení teploty a zbytek teče dál. Pro zjištění, kolik tepla se z toku “oddělí” a způsobí v daném místě navýšení teploty potřebujeme vědět, jak rychle v daném místě tok klesá jako funkce proměnné \(x\). Nárůst určíme derivací podle \(x\) a pokles z nárůstu uděláme změnou znaménka. Pokles toku tepla je tedy \[-\frac{\partial q}{\partial x}=
-\frac{\partial }{\partial x}\left(-k\frac{\partial T}{\partial x}\right)=
\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right).
\]
- Pokles toku vypočtený v předchozím bodě je úměrný rychlosti růstu teploty. Příslušné konstanty úměrnosti dodá fyzika a platí \[\frac{\partial}{\partial x}\left(k\frac{\partial T}{\partial x}\right)=\rho c\frac{\partial T}{\partial t},\] kde \(c\) je měrná tepelná kapacita a \(\rho\) je hustota. (V tomto případě jsou hustota i měrná tepelná kapacita vztaženy ne k jednotce objemu, jak jsme zvyklí, ale k jednotce délky. Například \(\rho\) je lineární hustota, tj. v gramech na centimetr).
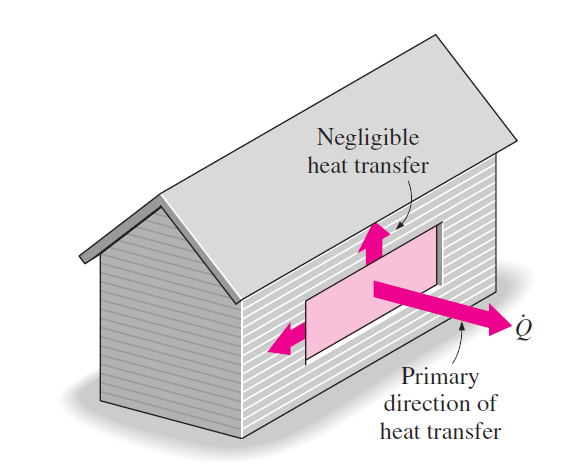
- Rovnice odvozená v předchozím kroku se nazývá rovnice vedení tepla a dokáže modelovat například prostup tepla stěnou domu.
Shrnutí. V odvození vidíme, že rovnice vedení tepla je vlastně bilance toku tepla. Rozdíl o kolik se v daném místě snižuje tok tepla udává, kolik tepla se v daném místě spotřebovalo. Tato spotřeba tepla se projeví zvýšením teploty v daném bodě.
Druhá derivace
Druhá derivace je derivace první derivace. U funkce dvou proměnných připadají v úvahu čtyři kombinace. Buď derivujeme pokaždé podle stejné proměnné, tj. \[
\frac{\partial^2 f}{\partial x^2}:=\frac{\partial}{\partial x}\frac{\partial f}{\partial x},\quad
\frac{\partial^2 f}{\partial y^2}:=\frac{\partial}{\partial y}\frac{\partial f}{\partial y},
\] nebo pokaždé podle jiné proměnné. Tady existují teoreticky dvě možnosti \[\frac{\partial }{\partial x}\frac{\partial f}{\partial y},
\frac{\partial}{\partial y}\frac{\partial f}{\partial x}\] Poději si ukážeme, že tyto dvě možnosti jsou v praxi zpravidla vždy totožné.
Je-li tepelná vodivost \(k\) v rovnici vedení tepla \[\rho c\frac{\partial T}{\partial t} = \frac{\partial}{\partial x}\left(k\frac{\partial T}{\partial x}\right)\] konstantní, redukuje se rovnice na rovnici \[\rho c\frac{\partial T}{\partial t} = k \frac{\partial^2 T}{\partial x^2},\] ve které figuruje druhá derivace podle polohy.
Numerická aproximace: konečné diference I
Základním přístupem při numerickém odhadu derivace je vynechání limitního přechodu v definici derivace. Pro funkci jedné proměnné a její derivaci \[\frac{\mathrm df}{\mathrm dx}=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\] tedy dostáváme \[\frac{\mathrm df}{\mathrm dx}\approx\frac{f(x+h)-f(x)}{h}.\] Okamžitá rychlost je nahrazena průměrnou rychlostí na intervalu \((x,x+h).\) Tento podíl se nazývá dopředná poměrná diference nebo zkráceně dopředná diference. Pokud použijeme tento postup pro parciální derivace, dostáváme \[\frac{\partial f}{\partial x}\approx\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}\] a \[\frac{\partial f}{\partial y}\approx\frac{f(x,y+\Delta y)-f(x,y)}{\Delta y}\]
Opakování: Taylorův polynom a polynomiální aproximace v 1D
V diferenciálním počtu funkcí jedné proměnné se zabýváme otázkou hledání nejlepší polynomiální aproximace nějaké funkce. Odpovědí je Taylorův polynom jako nejlepší polynomiální aproximace funkce
Věta (Taylorova věta pro kvadratickou aproximaci).
Platí \[f(x+h)=f(x)+\frac {\mathrm df(x)}{\mathrm dx}h+\frac{1}{2!} \frac {\mathrm d^2f(x)}{\mathrm dx^2} h^2+O(h^3),\] kde \(O(h^3)\) je funkce, která v okolí nuly konverguje k nule alespoň tak rychle, jako konstantní násobek funkce \(h^3\).
Numerická aproximace: konečné diference II
Přesnější aproximace derivace vychází z Taylorova polynomu druhého řádu napsaného pro \(f(x+h)\) a \(f(x-h)\), tj. ze vztahů \[\begin{aligned}
f(x+h)&\approx f(x)+f'(x)h+\frac 12 f''(x)h^2,\\
f(x-h)&\approx f(x)-f'(x)h+\frac 12 f''(x)h^2.
\end{aligned}\] Pokud tyto vztahy sečteme a odečteme, dostaneme \[\begin{aligned}
f(x+h)+f(x-h)&\approx2f(x)+ f''(x)h^2,\\
f(x+h)-f(x-h)&\approx2f'(x)h.
\end{aligned}\] Odsud dostáváme aproximace první a druhé derivace \[ f'(x)=\frac{\mathrm d f}{\mathrm dx}\approx \frac{f(x+h)-f(x-h)}{2h} \] a \[ f''(x)=\frac{\mathrm d^2f}{\mathrm dx^2}\approx \frac{f(x-h)-2f(x)+f(x+h)}{h^2}. \] Analogicky pro parciální derivaci podle \(x\) \[ \frac{\partial f}{\partial x}\approx \frac{f(x+\Delta x,y)-f(x-\Delta x,y)}{2\Delta x} \] a \[ \frac{\partial^2f}{\partial x^2}\approx \frac{f(x-\Delta x,y)-2f(x,y)+f(x+\Delta x,y)}{\Delta x^2}. \] Tato aproximace první derivace se nazývá centrální diference a je přesnější, než dopředná diference, protože je založena na přesnější aproximaci funkce \(f\). Používá totiž polynom druhého stupně, kdežto dopředná diference je založena pouze na lineární aproximaci.
Nutná dávka terminologie
V dalším budeme pracovat s pojmy jako množina a její hranice, množina obsahující hranici, množina neobsahující hranici, spojitá funkce apod. Ač v technicky nejvýznamnějších aplikacích často můžeme tyto pojmy chápat intuitivně, historie ukázala, že přesná formální definice je nezbytná.
V dalším nastane jedna z nejnebezpečnějších situací v matematice, kdy přesně definovanému pojmu dáme název, který lidé znají z prostého života. Například hranice, oblast, spojitost, uzávěr, okolí, … Podrobný rozbor ukazuje, že tyto definice jsou v jednoduchých případech v souladu s intuicí.
Euklidovský metrický prostor
Definice (metrický prostor, metrika).
Množina \(\mathbb{E}^3\) prvků z \(\mathbb{R}^3\) s metrikou \(\rho\) definovanou pro \(A=(a_x,a_y,a_z)\in\mathbb{R}^3\) a \(B=(b_x, b_y, b_z)\in\mathbb{R}^3\) vztahem \[
\rho(A,B)=\sqrt{(a_x-b_x)^2+(a_y-b_y)^2+(a_z-b_z)^2}
\] se nazývá Euklidovský metrický prostor. Prvky prostoru \(\mathbb{E}^3\) budeme nazývat body. Funkce \(\rho\) se nazývá Euklidovská metrika. Číslo \(\rho(A,B)\) se nazývá Euklidovská vzdálenost bodů \(A\), \(B\).
Analogicky je možno definovat metriku v prostoru libovolné konečné dimenze.
Definice (okolí).
Buď \(A\in \mathbb{E}^n\) bod z \(\mathbb{E}^n\) a \(\varepsilon>0\) kladné reálné číslo. Epsilonovým okolím bodu \(X\) rozumíme množinu označenou \(O_\varepsilon(A)\) skládající se z bodů, jejichž vzdálenost od bodu \(A\) je menší než \(\varepsilon\), tj. \[
O_\varepsilon(A)=\{X\in\mathbb{E}^n:\rho(A,X)<\varepsilon\}.
\] Ryzím epsilonovým okolím bodu \(A\) rozumíme množinu \(\overline O_\varepsilon(A)\) definovanou \[
\overline O_\varepsilon(A)=O_\varepsilon(A)\setminus\{A\},
\] tj. \(\varepsilon\)-okolí bodu \(A\), s vyloučením bodu \(A\).
Významné vlastnosti množin v Euklidovském prostoru
V následujících definicích je \(X\in\mathbb{E}^n\) bod a \(M\subseteq \mathbb{E}^n\) podmnožina v Euklidovském prostoru \(\mathbb{E}^n\) (\(n=2\) nebo \(3\)). Abstraktně je možno s těmito pojmy pracovat i v prostorech libovolné konečné dimenze.
Ohraničená množina: Množina \(M\) se nazývá ohraničená, jestliže leží v (dostatečně velkém) okolí nějakého bodu \(Y\in\mathbb{E}^n\).
Vnitřní bod, vnitřek, otevřená množina: Bod \(X\) se nazývá vnitřním bodem množiny \(M\), jestliže \(X\in M\) a existuje nějaké okolí \(O(X)\) bodu \(X\) ležící celé v množině \(M\), tj. \(O(X)\subseteq M\). Množina všech vnitřních bodů množiny \(M\) se nazývá a označuje \(M^o\). Je-li množina \(M\) totožná se svým vnitřkem, tj. je-li každý bod množiny \(M\) vnitřní, říkáme, že množina \(M\) je otevřená.
Hraniční bod, hranice: Bod \(X\) se nazývá hraničním bodem množiny \(M\), jestliže každé okolí bodu \(X\) obsahuje alespoň jeden bod ležící v množině \(M\) a současně alespoň jeden bod neležící v množině \(M\). Množina všech hraničních bodů množiny \(M\) se nazývá hranice množiny \(M\) a označuje \(\partial M\).
Uzávěr, uzavřená množina: Uzávěrem množiny \(M\) rozumíme množinu \(\overline M\) definovanou jako sjednocení vnitřku a hranice množiny \(M\), tj. \(\overline M=M^o\cup\partial M\). Je-li množina totožná se svým uzávěrem (tj. obsahuje-li všechny své hraniční body), nazývá se uzavřená.
Souvislá množina: Množina \(M\) se nazývá souvislá, jestliže každé dva body, ležící v množině \(M\) lze spojit lomenou čarou, ležící v \(M\).
Oblast, uzavřená oblast, kompaktní množina: Otevřená souvislá množina se nazývá oblast. Uzavřená souvislá množina se nazývá uzavřená oblast. Uzavřená ohraničená množina se nazývá kompaktní.
Spojitost funkce
Spojitost skalární funkce: Nechť \(f:\mathbb{R}^n\to \mathbb{R}\) je skalární funkce \(n\) proměnných definovaná v nějakém okolí bodu \(A\in\mathbb{R}^n\). Řekneme, že funkce \(f\) je v bodě \(A\) spojitá, pokud pro každé okolí \(O(f(A))\) bodu \(f(A)\) existuje okolí \(\overline O(A)\) bodu \(A\) takové, že obrazy všech bodů z tohoto okolí bodu \(A\) leží v okolí bodu \(O(f(A))\), tj. pro všechna \(X\in \overline O(A)\) platí \(f(X)\in O(f(A))\).
Spojitost vektorové funkce: Nechť \(f:\mathbb{R}^n\to \mathbb{R}^m\) je vektorová funkce \(n\) proměnných definovaná v nějakém okolí bodu \(A\in\mathbb{R}^n\). Řekneme, že funkce \(f\) je v bodě \(A\) spojitá, jestliže je v tomto bodě spojitá každá její komponenta.
Elementární funkce: Všechny mnohočleny, goniometrické, cyklometrické, exponenciální a logaritmické funkce a obecná mocnina se nazývají základní elementární funkce Všechny funkce, které ze základních elementárních funkcí získáme konečným počtem operací sčítání, odečítání, násobení, dělení a skládání těchto funkcí navzájem se nazývají elementární funkce.
Elementární funkce jsou tedy všechny funkce, které umíme v konečném tvaru vyjádřit explicitním vzorcem za použití funkcí známých ze střední školy a cyklometrických funkcí.
Elementární neznamená jednoduchý. Funkce \[f(x,y)=\frac{x^2+\sin(x^2-y^2)}{\ln(x^2+y^2-1)},\quad g(x,y)=\frac{1}{1+\frac x{1+\frac {y}{x^2}}} \] jsou elementárními funkcemi ve smyslu výše uvedené definice. Funkce \[h(x,y)=\begin{cases} 1 & x=0 \text{ nebo }y=0\\0 &\text{jinak}\end{cases}\] není elementární funkce.
Následující věta ukazuje, že u elementárních funkcí je spojitost v libovolném bodě zaručena již tím, že je funkce v tomto bodě definována.
Věta (spojitost elementárních funkcí).
Všechny elementární funkce jsou spojité v každém vnitřním bodě svého definičního oboru.
Schwarzova věta
Věta (Schwarzova).
Jsou-li smíšené derivace spojité na otevřené množině, jsou zde stejné, tj. platí \[ \frac{\partial }{\partial x} \frac{\partial f}{\partial y}= \frac{\partial }{\partial y} \frac{\partial f}{\partial x}.\]
Vzhledem k této větě existují jenom tři druhé parciální derivace. Je tedy bezpečné psát \[
\frac{\partial^2 f}{\partial x^2},\quad
\frac{\partial^2 f}{\partial x \partial y},\quad
\frac{\partial^2 f}{\partial y^2},
\] nebo \[f''_{xx},\quad f''_{xy},\quad f''_{yy}.\]