Vybrané postupy numerické matematiky
Robert Mařík
listopad 2019, prosinec 2020
Numerické řešení diferenciálních rovnic
Již v prvním týdnu jsme se při zdůraznění role derivace dostali k formulování modelů použitím derivací, k diferenciálním rovnicím. Tyto rovnice je možné pro konkrétní hodnoty parametrů a konkrétní počáteční podmínku řešit numericky.
Následující přehlídka znovu připomene některé modely a odkaz za těmito modely vede na interaktivní nástroj pro numerické řešení. Tímto nástrojem můžeme vizualizovt řešení pro různé počáteční podmínky. Pro náročnější práci, jako například vizualizace různých rovnic (například pro různé nastavení parametrů) by bylo nutné použít nějaký neinteraktivní nástroj, kde se ve speciálním jazyce naformuluje model, nastaví parametry, spustí řešič a vykreslí řešení.
- Model ochlazování kávy \[\frac{\mathrm dT}{\mathrm dt}=-k (T-T_0)\]
- Model růstu populace v prostředí s omezenou nosnou kapacitou \[\frac{\mathrm dx}{\mathrm dt}=rx\left (1-\frac xK \right)\] Neinteraktivní model, který vypočte 1000 řešení pro 1000 kombinací hodnot \(r\) a \(K\) je zde. Podobné analýzy se dělají, pokud jsou koeficienty v rovnici zatíženy chybou a chceme vědět, jak se tato chyba projevuje na řešení. V takovém případě nestačí “klikací” přístup, ale je možné udělat dostatečný počet simulací s vhodně nastavenými paraemtry a tyto statisticky vyhodnotit.
- Model růstu vodní kapky v atmosféře \[\frac{\mathrm dV}{\mathrm dt}=k V^{2/3}\]
- Model růstu ledu podle Stefanova zákona \[\frac{\mathrm dh}{\mathrm dt}=\frac kh\]
Všimněte si, že v numerickém modelu je prostým pohledem prakticky nerozlišitelný model růstu vodní kapky od modelu růstu úměrného velikost populace (změňte si mocninu \(\frac 23\) na \(1\)), ale modely se chovají principiálně zcela jinak, protože v jednom je zaručena jednoznačnost řešení a ve druhém je tato jednoznačnost porušena. Dále si všimněte, že model růstu ledu má při prodlužování řešení zpět v čase evidentně problémy s nulou ve jmenovateli. Abychom různé parazitní výstupy numerických algoritmů jako je zde dokázali odchytit a eliminovat, nestačí “umět rovnici naklikat do programu”, ale znalost teorie a kvalitativních vlastností řešení je téměř nezbytná pro jakoukoliv závažnější práci.
Numerické řešení diferenciálních rovnic ve 2D a 3D
Pokud máme v zásobě zkušenosti s modelováním diferenciálních rovnic, můžeme se pustit do odvážnějších aplikací, jako třeba následující modely.
Konkurence dvou populací
Dynamika rozvoje jedné populace může být ovlivněna přítomností druhé populace. Například pokud se dvě populace navzájem brzdí v růstu, je vhodným modelem soustava rovnic \[ \begin{aligned} \frac{\mathrm dx}{\mathrm dt}=r_xx\left(1-\frac x{K_x} - ay\right),\\ \frac{\mathrm dy}{\mathrm dt}=r_yy\left(1-\frac y{K_y} - bx\right). \end{aligned} \] V chování této soustavy je možno podle nastavení parametrů pozorovat všechny možné situace pozorované v přírodě, což zahrnuje dominanci jednoho z druhů, slabou konkurenci druhů nebo silnou konkurenci druhů. Více viz učebnice z populační ekologie.
Model dravce a kořisti
Dynamika rozvoje ineragujících populací dravce a kořisti může být vyjádřena Lotkovým Volterrovým modelem \[ \begin{aligned} \frac{\mathrm dx}{\mathrm dt}=ax-bxy,\\ \frac{\mathrm dy}{\mathrm dt}=cxy-dy. \end{aligned} \] V chování této soustavy je možno pozorovat oscilace obou populací přesně tak, jako to vídáme v přírodě. Další pozorované situace model nevysvětluje, protože je jednoduchý. Jedná se však o základní stavební kámen, který je možno dále zpřesňovat a modelovat situaci blíže konkrétní aplikaci.
Model epidemie
Populaci rozdělíme na tři skupiny.
- Skupina S (angl. susceptible) obsahuje tu část populace, které je náchylná k onemocnění. Tito jedinci netrpí chorobou, mohou však být infikováni při styku s nemocnými.
- Skupina I (angl. infected) obsahuje část populace tvořenou infikovanými jedinci. Tito jedinci vykazují známky onemocnění a rozšiřují nemoc mezi členy skupiny \(S\).
- Skupina R (angl. removed) obsahuje tu část populace, která je tvořena jedinci, kteří byli dříve infikováni, ale nyní již nemohou šířit chorobu.
Velikosti skupin S, I a R budeme označovat \(S\), \(I\) a \(R\). Předpoklady, že počet osob které onemocní za jednotku času souvisí s počtem náchylných a infikovaných a že počet osobn, které jsou izolovány souvisí s počtem infikovaných vede k soustavě diferenciálních rovnic (Kermack-McKendrik(1927)) \[ \begin{aligned} \frac{\mathrm dS}{\mathrm dt}&=-\alpha SI,\\ \frac{\mathrm dI}{\mathrm dt}&=\alpha SI-\beta I,\\ \frac{\mathrm dR}{\mathrm dt}&=\beta I\\ \end{aligned} \]
Matematicky je možno chování modelu studovat i bez explicitní formulace diferenciálních rovnic, pouze využitím takzvaného kompartmentového modelu. Tímto způsobem je možno relativně snadno přidávat do modelu skupinu bepříznakových, vakcinovaných, skupinu v inkubační době a podobně.
Nondimenzionalizace a bezrozměrné veličiny
Rovnice vedení tepla v jedné dimenzi (prostup tepla stěnou, vedení tepla tyčí) má tvar (viz minulá přednáška) \[\rho c \frac{\partial T}{\partial t}=\frac{\partial }{\partial x} \left(D\frac{\partial T}{\partial x}\right),\] kde \(T(x,t)\) je teplota v místě \(x\) a čase \(t\), \(\rho\) je hustota, \(c\) je měrná tepelná kapacita, \(D\) je teplotní vodivost. Pro homogenní stěnu nebo tyč a lineární materiálovou odezvu je \(D\) konstanta a můžeme ji vytknout z derivace na pravé straně a psát \[\rho c \frac{\partial T}{\partial t}=D\frac{\partial^2 T}{\partial x^2}.\] Pro úplnou formulaci úlohy na nalezení teploty v jednotlivých místech stěny musíme zadat polohu stěny, teplotu na vnějším a vnitřním okraji stěny a počáteční rozložení teploty ve stěně. Nechť tedy okraje jsou \(x=0\) a \(x=L\), a teploty na okrajích a počáteční rozložení teploty jsou \[\begin{aligned}T(0,t)&=T_0\\T(L,t)&=T_1\\ T(x,0)&=f(x)\end{aligned}.\] Analogicky jako u obdobného příkladu s chladnutím tělesa podle Newtonova zákona (viz přednáška o diferenciálních rovnicích) zavedeme bezrozměrnou teplotu tak, aby se podmínky na okrajích redukovaly na konstanty. Zavedeme-li bezrozměrnou teplotu \[\xi(x,t) =\frac{T(x,t)-T_0}{T_1-T_0}\] a bezrozměrnou vzdálenost \(\mu =\frac xL\), redukuje se model podle stejných pravidel, jaká jsme poznali u obyčejných rovnic, na \[\begin{aligned} \rho c \frac{\partial \xi}{\partial t}&=D\frac 1{L^2}\frac{\partial ^2 \xi}{\partial \mu^2},\\ \xi(0,t)&=0,\\ \xi(1,t)&=1,\\ \xi(\mu,t)&=f_\xi(\mu), \end{aligned}\] kde \(f_\xi(\mu)\) je počáteční rozložení teploty transformované do nových veličin. Přepíšeme-li rovnici na tvar \[\frac 1{\frac {D}{L^2\rho c}} \frac{\partial \xi}{\partial t}=\frac{\partial ^2 \xi}{\partial \mu^2},\] vidíme, že zavedení bezrozměrného času vztahem \(\tau=\frac{Dt}{\rho c L^2}\) redukuje úlohu z původního tvaru (kde každý člen má svůj fyzikální význam a přímou interpretaci) \[\boxed{\begin{aligned} \rho c \frac{\partial T}{\partial t}&=D\frac{\partial ^2 T}{\partial x},\\ T(0,t)&=T_0,\\ T(L,t)&=T_1,\\ T(x,t)&=f(x), \end{aligned}}\] na tvar \[\boxed{\begin{aligned} \frac{\partial \xi}{\partial \tau}&=\frac{\partial ^2 \xi}{\partial \mu^2},\\ \xi(0,\tau )&=0,\\ \xi(1,\tau )&=1,\\ \xi(\mu, 0)&=f_\xi(\mu), \end{aligned}}\] který je mnohem jednodušší pro následnou numerickou analýzu nebo analytické studium. Mimo jiné je tím ukázáno, že pro danou úlohu nemají podstatný význam jednotlivé veličiny samy o sobě, ale veličina \(\tau = \frac{Dt}{\rho c L^2}\), definující bezrozměrný čas. Tato veličina se nazývá Fourierovo číslo. Obdobným postupem získáme jiná čísla důležitá pro popis jiných procesů, jako jsou Biotovo číslo (vedení tepla), Reynoldsovo číslo (proudění tekutin), Froudeho číslo (proudění tekutin) apod. Podobná nondimenzionalizace pro vlhkostní pole ve dřevě je v publikaci Horáček P., Fyzikální a mechanické vlastnosti dřeva. Viz též eopora, rovnice (144) a rovnice následující.
Metoda konečných diferencí
Vraťme se s aparátem matematického popisu vedení tepla k úloze hledání rozložení teploty na čtvercové desce, kterou jsme představili v přednášce o lineární algebře: Je dána deska čtvercového tvaru, jejíž okraje udržujeme na konstatních teplotách (každý okraj obecně na jiné teplotě) a hledáme rovnovážné rozložení teploty. Dvourozměrná rovnice vedení tepla pro homogenní izotropní desku s materiálovými charakteristikami \(\rho\), \(c\) a \(D\) má tvar \[\rho c \frac{\partial T}{\partial t}=D\frac{\partial^2 T}{\partial x^2}+D\frac{\partial^2 T}{\partial y^2}.\] Ve stacionárním stavu se teplota nemění s časem a proto je levá strana nulová a rovnice se redukuje na \[\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}=0.\]
Použijeme stejnou myšlenku jako v lineární algebře: rozdělíme desku čtvercovou sítí na malé oblasti a budeme studovat teplotu v bodech této sítě, tj. v rozích jednotlivých čtverců, na které je deska čtvercovou sítí rozdělena.
Z přednášky o derivacích a aproximaci víme, že funkci můžeme aproximovat v okolí námi zvoleného bodu Taylorovým polynomem a v kapitole o diferenciálních rovnicích jsme tuto aproximaci použili pro aproximaci druhé derivace konečnými diferencemi ve tvaru \[f''(x)\approx \frac{1}{h^2}[f(x+h)-2f(x)+f(x-h)].\] Podobně pro parciální derivace funkce dvou proměnných \(f(x,y)\) dostáváme
\[\begin{aligned} \frac {\partial ^2 f}{\partial x^2}&\approx \frac{1}{h^2}[f(x+h,y)-2f(x,y)+f(x-h,y)]\\ \frac {\partial ^2 f}{\partial y^2}&\approx \frac{1}{h^2}[f(x,y+h)-2f(x,y)+f(x,y-h)] \end{aligned} \] a odsud \[ \frac {\partial ^2 f}{\partial x^2} + \frac {\partial ^2 f}{\partial y^2} \approx \frac{1}{h^2}[f(x+h,y)+f(x-h,y)+f(x,y+h)+f(x,y-h)-4f(x,y)]. \] Z rovnice \[\frac {\partial ^2 f}{\partial x^2} + \frac {\partial ^2 f}{\partial y^2} =0,\] popisující rozložení teploty vyplývá, že výraz v hranaté závorce musí být nulový, tj. \[f(x,y)=\frac 14 [f(x+h,y)+f(x-h,y)+f(x,y+h)+f(x,y-h)].\] To však znamená, že teplota v každém uzlovém bodě je průměrem teplot v okolních uzlových bodech. Přesně, jak jsme se (možná poněkud naivně) domnívali při představení úlohy v přednášce z lineární algebry. Nyní tento postup stavíme na solidní vědecký základ, založený na rovnici popisující fyzikální proces (rovnice vedení tepla) a na numerické aproximaci, která převede parciální diferenciální rovnici na soustavu lineárních rovnic.
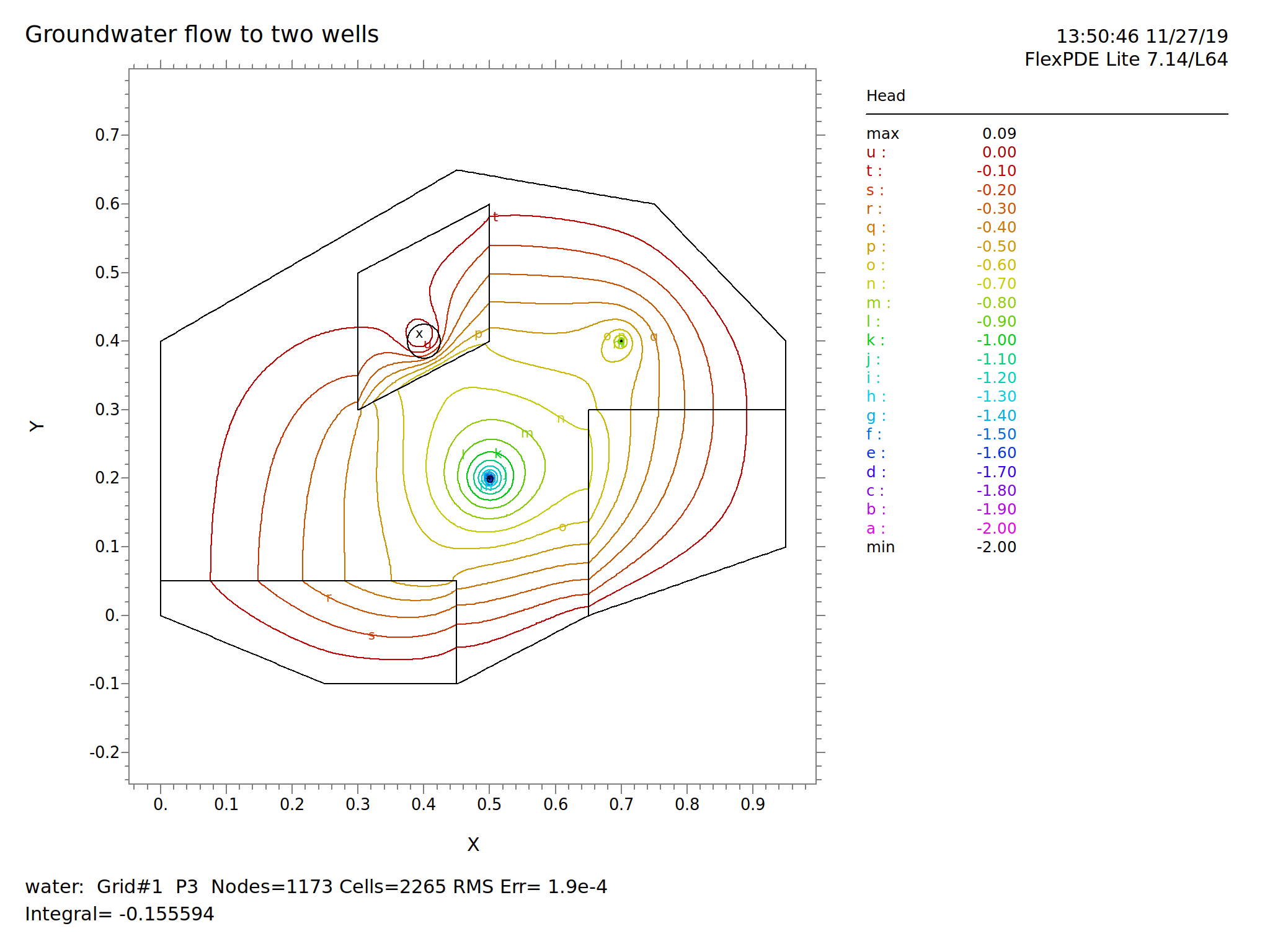
Výše popsaná myšlenka je základem metody konečných diferencí. Bohužel je tato metoda poměrně omezená nutností, mít ekvidistantní rozložení uzlů. Proto se v praxi používají vyspělejší metody, metoda konečných prvků nebo metoda konečných objemů. Základní myšlenka je stejná (parciální diferenciální rovnice se převede na soustavu lineárních rovnic) a praktické provedení zpravidla matematicky triviální, protože vše potřebné pro výpočty je předprogramováno v softwaru určenému pro danou úlohu. Máme takto software umožňující simulovat vedení tepla, tepelné úniky, tepelné nebo mechanické namáhání, tok podzemní i povrchové vody a další důležité praktické aplikace. Uživatel jenom zadá geometrii, typ problému a okrajové a počáteční podmínky a program vypočte potřebná řešení a dle požadavků je různým způsobem interpretuje.
Ukázka programu FlexPDE
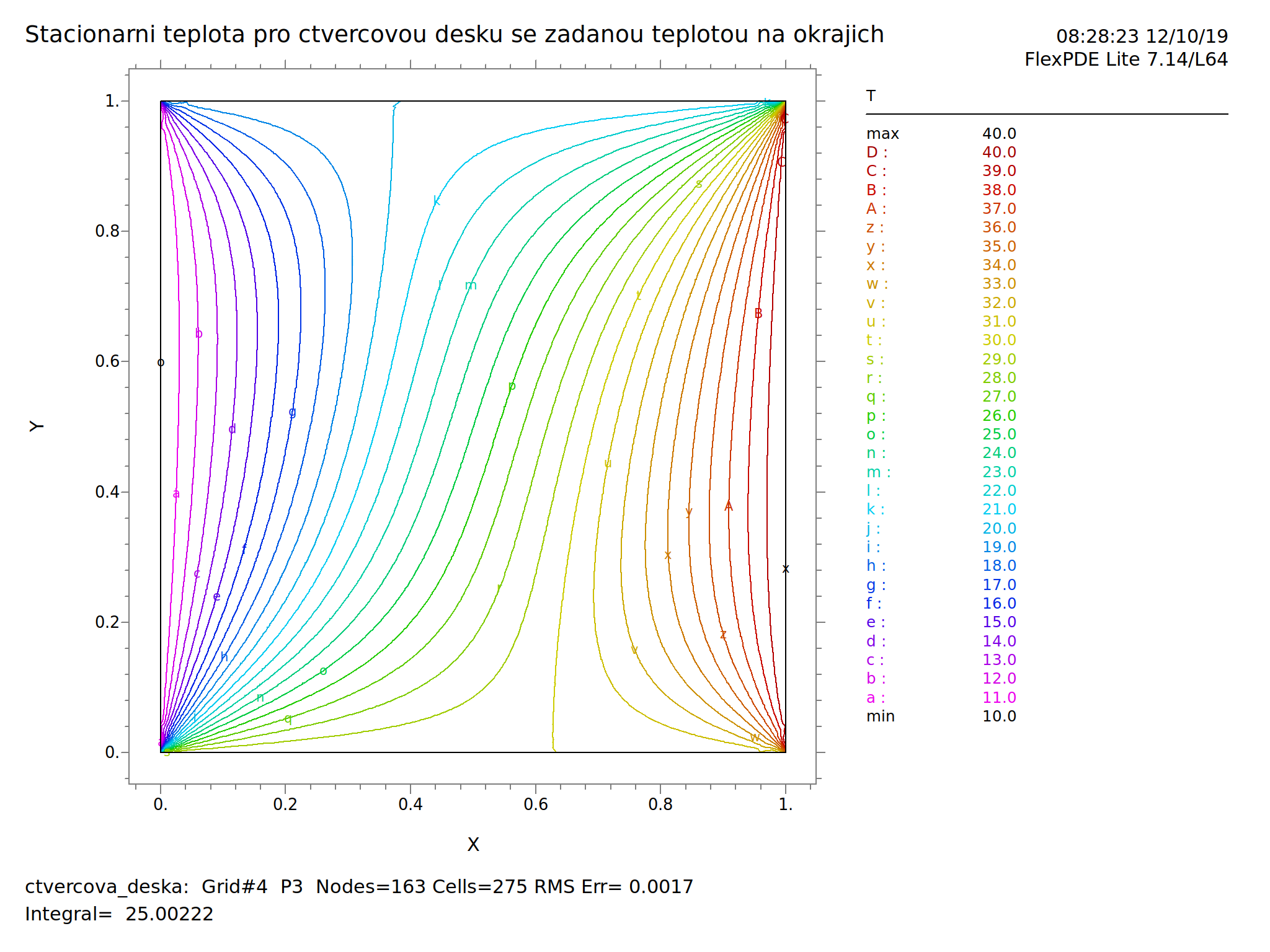
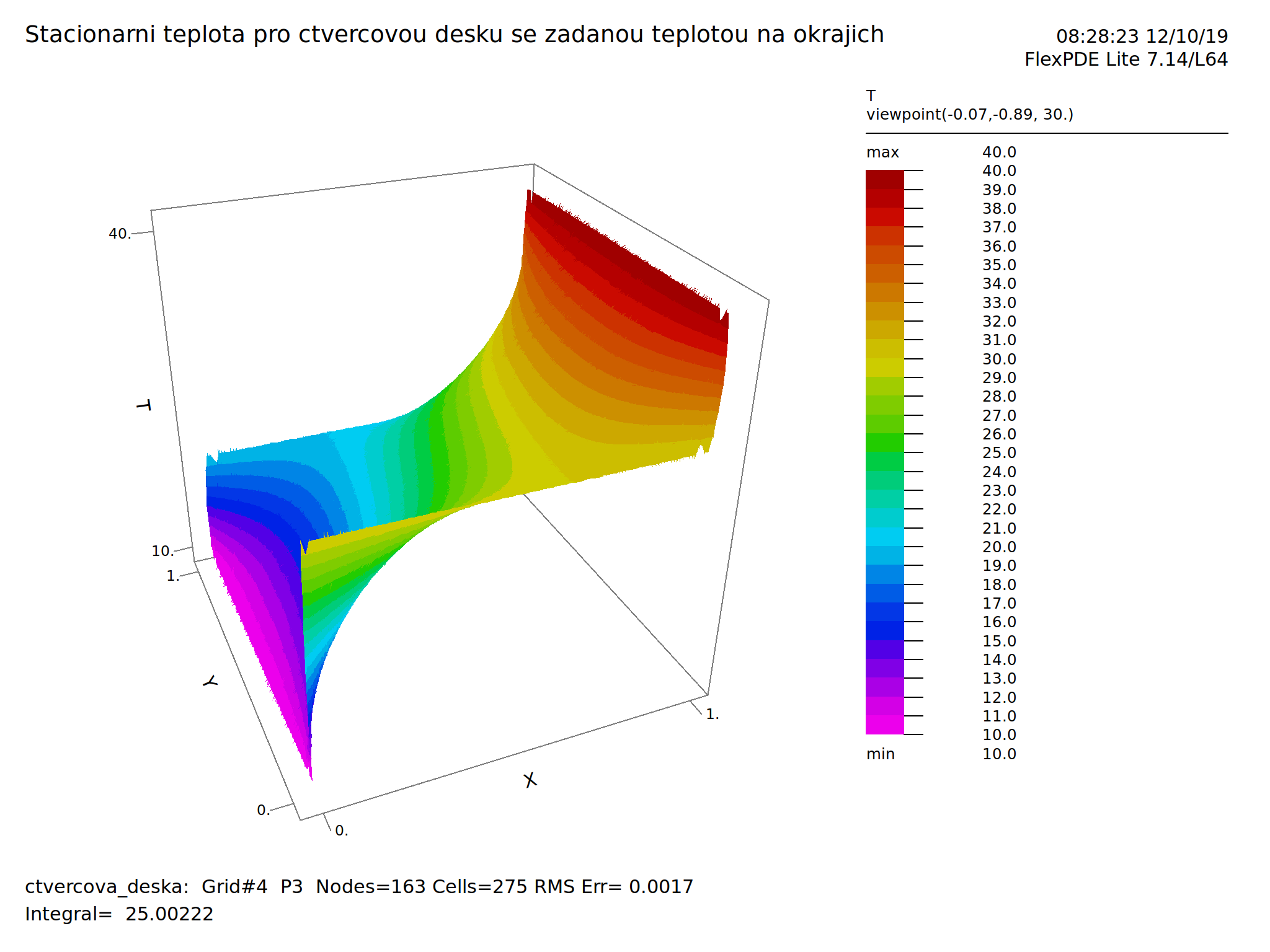
Existuje široká škála programů pro řešení diferenciálních rovnic. V mnoha jsou předpřipravené modely, předdefinované fyzikální úlohy a někdy dokonce databáze materiálových vlastností. V jiných programech je řešená rovnice plně pod kontrolou autora modelu a je možné snadno řešit i multifyzikální úlohy (například současně modelovat teplotu a vlhkost v materiálu). Zástupce druhé skupiny je FlexPDE firmy PDE Solutions Inc. Úloha s rozložením tepoty na čtvercové desce se zadanými teplotami na okrajích, na kterou jsme několikrát jako na motivaci narazili v lineární algebře a připomněli na předchozím slidu, by měla následující zápis a výstup.
TITLE 'Stacionarni teplota pro ctvercovou desku se zadanou teplotou na okrajich'
VARIABLES T
EQUATIONS T: div(grad(T))=0
INITIAL VALUES T=10
BOUNDARIES
REGION 1
START(0,0) VALUE(T)=30 LINE TO (1,0)
VALUE(T)=40 LINE TO (1,1)
VALUE(T)=20 LINE TO (0,1)
VALUE(T)=10 LINE TO CLOSE
PLOTS
CONTOUR(T)
SURFACE(T)
ENDRovnice je v popisu modelu zadána jako divergence gradientu, což v kartézských souřadnicích ve 2D vede právě na rovnici \[\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}=0.\] Jiná forma zápisu je přímo pomocí druhých parciálních derivací ve tvaru DXX(T)+DYY(T)=0.
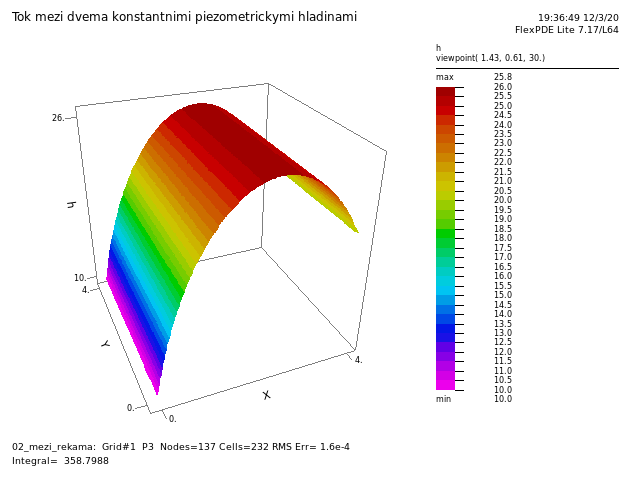
Poslední model je model podzemní vody s konstantními piezometrickýmí hladinami podél dvou rovnoběžných stran (mohou být například dvě řeky) a s rovnoměrně rozloženými zdroji (například nad oblastí jsou rovnoměrné srážky a voda rovnoměrně zasakuje). Řešením modelu vidíme odkud teče voda do které řeky. Tím je možno například usuzovat, kde po případné kontaminaci provádět sanační práce.