Varianty zápisu soustavy lineárních rovnic

Uvažujme následující tři problémy:

1. Najděte všechna reálná čísla \(x_1\), \(x_2\), splňující dvojici rovnic \[ \begin{aligned} 4x_1&+5x_2=7\\ \phantom{4}x_1&-2x_2=4 \end{aligned} \]
2. Najděte všechna reálná čísla \(x_1\), \(x_2\), splňující vektorovou rovnici \[ \begin{aligned} \begin{pmatrix} 4\\1 \end{pmatrix} x_1 + \begin{pmatrix} 5\\-2 \end{pmatrix} x_2 = \begin{pmatrix} 7\\4 \end{pmatrix} \end{aligned}\]
3. Najděte všechna reálná čísla \(x_1\), \(x_2\), splňující maticovou rovnici \[\begin{aligned} \begin{pmatrix} 4&5\\1&-2 \end{pmatrix} \begin{pmatrix} x_1\\x_2 \end{pmatrix} = \begin{pmatrix} 7\\4 \end{pmatrix} \end{aligned} \]

Všechny problémy jsou ekvivalentní a jedná se o jiný zápis téhož. Jednou však používáme soustavu rovnic, vektory a jejich lineární kombinaci a jednou matice a maticový součin!

Soustava lineárních rovnic

Definice (soustava lineárních rovnic).

Soustavou \(m\) lineárních rovnic o \(n\) neznámých nazýváme soustavu rovnic \[ \tag{1} \begin{gathered} a_{11}x_1+a_{12}x_2+a_{13}x_3+\cdots+a_{1n}x_n=b_1 \\ a_{21}x_1+a_{22}x_2+a_{23}x_3+\cdots+a_{2n}x_n=b_2 \\ a_{31}x_1+a_{32}x_2+a_{33}x_3+\cdots+a_{3n}x_n=b_3 \\ \vdots \\ a_{m1}x_1+a_{m2}x_2+a_{m3}x_3+\cdots+a_{mn}x_n=b_m \end{gathered} \] Proměnné \(x_1\), \(x_2\), , \(x_n\) nazýváme neznámé. Reálná čísla \(a_{ij}\) nazýváme koeficienty levých stran, reálná čísla \(b_j\) koeficienty pravých stran soustavy rovnic. Řešením soustavy rovnic rozumíme uspořádanou \(n\)-tici reálných čísel \([t_1, t_2, \ldots, t_n]\) po jejichž dosazení za neznámé (v tomto pořadí) do soustavy dostaneme ve všech rovnicích identity.

Definice (matice soustavy).

Matici \[ A=\left( \begin{matrix} a_{11}& a_{12}& a_{13}& \cdots{}& a_{1n}\\ a_{21}& a_{22}& a_{23}& \cdots{}& a_{2n}\\ \vdots{} &\vdots{}& {} &\ddots{}& \vdots{}\\ a_{m1}& a_{m2}& a_{m3}& \cdots{}& a_{mn}\\ \end{matrix}\right) \] nazýváme maticí soustavy (1). Matici \[ A_r=\left( \begin{array}{ccccc|c} a_{11}& a_{12}& a_{13}& \cdots{}& a_{1n}&b_1\\ a_{21}& a_{22}& a_{23}& \cdots{}& a_{2n}&b_2\\ \vdots{} &\vdots{}& {} &\ddots{}& \vdots{}&\vdots\\ a_{m1}& a_{m2}& a_{m3}& \cdots{}& a_{mn}&b_m\\ \end{array} \right) \] nazýváme rozšířenou maticí soustavy (1).

Vektorový zápis soustavy lineárních rovnic

Soustavu (1) lze ekvivalentně přepsat do vektorového tvaru \[ \begin{pmatrix} a_{11}\\a_{21}\\\vdots\\a_{m1} \end{pmatrix} x_1+ \begin{pmatrix} a_{12}\\a_{22}\\\vdots\\a_{m2} \end{pmatrix} x_2+ \begin{pmatrix} a_{13}\\a_{23}\\\vdots\\a_{m3} \end{pmatrix} x_3+\cdots+ \begin{pmatrix} a_{1n}\\a_{2n}\\\vdots\\a_{mn} \end{pmatrix} x_n= \begin{pmatrix} b_{1}\\b_{2}\\\vdots\\b_{m} \end{pmatrix}. \] Vidíme tedy, že se vlastně jedná o problém, vyjádřit vektor složený z čísel na pravé straně soustavy rovnic jako lineární kombinaci vektorů, které tvoří sloupce matice soustavy.

Maticový zápis soustavy lineárních rovnic

Soustavu (1) lze ekvivalentně přepsat do maticového tvaru pomocí maticového součinu \[ \left( \begin{matrix} a_{11}& a_{12}& \cdots{}& a_{1n}\\ a_{21}& a_{22}& \cdots{}& a_{2n}\\ \vdots{} &\vdots{} &\ddots{}& \vdots{}\\ a_{m1}& a_{m2}& \cdots{}& a_{mn}\\ \end{matrix}\right) \left( \begin{matrix} x_1\\x_2\\ \vdots \\x_n \end{matrix} \right) = \left( \begin{matrix} b_1\\b_2\\ \vdots \\b_m \end{matrix} \right). \] Tento tvar se používá často v inženýrských výpočtech pro úspornost. Symbolicky zpravidla píšeme soustavu lineárních rovnic ve tvaru \[ A\vec x=\vec b, \] nebo \[AX=B\] kde \(A\) je matice soustavy a \(\vec b\) resp. \(B\) je vektor pravých stran.

Hodnost matice

Matice řádu \(m\times n\) obsahuje celkem \(m\cdot n\) čísel. Jedná se tedy o relativně komplikovaný objekt. V matematice se často snažíme složitější objekty nějakým způsobem charakterizovat pomocí objektů jednodušších, např. pomocí čísel. Jedno už známe, determinant. Dalším z těchto čísel je hodnost matice, kterou si nadefinujeme nyní.

Definice (hodnost matice).

Buď \(A\) matice. Hodností matice rozumíme maximální počet lineárně nezávislých řádků matice. Hodnost matice \(A\) označujeme \({h(A)}\).

Poznámka: Hodnost je v anglické literatuře označována jako rank.

Schodovitý tvar jsme si představili u determinantu. U matice ve schodovitém tvaru je určení determinantu velmi jednoduché. Podobný efekt vidíme i u hodnosti.

Definice (schodovitý tvar).

Řekneme, že matice \(A\) je ve schodovitém tvaru, jestliže případné nulové řádky jsou uspořádány na konci matice a nenulové jsou uspořádány tak, že každý následující řádek začíná větším počtem nul než řádek předchozí.

Věta (hodnost matice ve schodovitém tvaru).

Hodnost matice, která je ve schodovitém tvaru je rovna počtu jejích nenulových řádků.

Příklad. Matice \(A= \begin{pmatrix} 2&2&2&3&-1&5\\ 0&0&1&0&0&3\\ 0&0&0&-1&2&1\\ 0&0&0&0&0&0 \end{pmatrix}\) je ve schodovitém tvaru a \(h(A)=3\). Matice \(B= \begin{pmatrix} 2&2&2&3&-1&5\\ 0&0&1&0&0&3\\ 0&0&3&-1&2&1 \end{pmatrix}\) není ve schodovitém tvaru a její hodnost na první pohled nepoznáme.

Výpočet hodnosti

Výpočet hodnosti se provádí postupným nahrazením zadané matice maticí, která má stejnou hodnost, ale postupně se přibližuje schodovitému tvaru. Uvedeme si jenom základní postup. Tento se sice dá vylepšit, pro nás je však důležité, že i bez jakýchkoliv vylepšení vždy vede k cíli. (Alespoň teoreticky.)

Věta (řádkové operace zachovávající hodnost matice).

Následující operace nemění hodnost matice:

1. vynechání řádku složeného ze samých nul, nebo vynechání řádku, který je totožný s jiným řádkem, nebo vynechání řádku, který je násobkem jiného řádku,
2. vynásobení nebo vydělení libovolného řádku nenulovým číslem,
3. záměna pořadí řádků,
4. ponechání jednoho řádku beze změny a opakované přičtení libovolných násobků tohoto řádku k nenulovým násobkům ostatních řádků matice.

Libovolnou matici lze konečným počtem těchto úprav převést do schodovitého tvaru.

Následující věta udává, že veškerá tvrzení, uvedená v souvislosti s hodností pro řádky matice, se dají přeformulovat i pro sloupce matice.

Věta.

Transponování nemění hodnost matice.

Existence a jednoznačnost řešení soustavy lineárních rovnic

V případě, že matice soustavy je čtvercová již víme, že řešení je určeno jednoznačně právě tehdy, když má matice soustavy matici inverzní. O počtu řešení v obecném případě obdélníkové matice, kdy matici inverzní nemá smysl uvažovat, nám dávají informaci dvě následující věty. První se týká existence řešení a druhá identifikuje případ, kdy řešení je určeno jednoznačně.

Věta (Frobeniova věta, Kronecker-Capelliho věta).

Soustava lineárních rovnic je řešitelná právě tehdy, když její matice soustavy a rozšířená matice soustavy mají stejnou hodnost.

Věta (jednoznačnost řešení).

Nechť soustava lineárních rovnic má řešení. Toto řešení je právě jedno, pokud je společná hodnost matice soustavy a rozšířené matice soustavy rovna počtu neznámých. V opačném případě je společná hodnost matice a rozšířené matice soustavy menší než počet neznámých.

Gaussova eliminace

Spočívá v reprezentaci soustavy pomocí rozšířené matice soustavy a převodu této matice na schodovitý tvar pomocí řádkových operací zachovávajících hodnost. Tyto operace zachovávají i množinu řešení soustavy. Jakmile je matice ve schodovitém tvaru, zpětnou substitucí postupně dopočítáváme jednotlivé proměnné. (Formálně to u čtvercových regulárních matic odpovídá použití inverzní matice k matici, která má pod hlavní diagonálou nuly. Ale postup funguje i pro obecnější matice a dá se realizovat jednoduchými prostředky a postupným dosazováním.)

Gaussova eliminace je velice flexibilní a univerzální, umožní nám řešit i soustavy mající nekonečně mnoho řešení. V tomto případě dokážeme zapsat řešení pomocí parametrů.

Příklad.

\[ \begin{aligned} x_1+2x_2+2x_3+x_4&=0\\ x_1-x_2+x_3-2x_4&=1\\ x_2-2x_3+x_4&=2 \end{aligned} \]

Rozšířená matice soustavy je \[\left( \begin{array}{cccc|c} 1& 2& 2& 1& 0\\ 1& -1& 1& -2& 1\\ 0& 1& -2& 1& 2 \end{array}\right) \]

V prvním kroku převedeme na tvar, kdy jednom jeden řádek začíná nenulovým prvkem. První řádek už nijak neupravujeme a opíšeme jej. Místo druhého řádku napíšeme jeho součet s \((-1)\)-násobkem prvního řádku. \[ \left( \begin{array}{cccc|c} 1& 2& 2& 1& 0\\ 0& -3& -1& -3& 1\\ 0& 1& -2& 1& 2 \end{array}\right) \]

V dalším kroku převedeme na tvar, kdy z řádků začínajících jednou nulou ponecháme jenom jeden a ostatní upravíme tak, aby začínaly alespoň dvěma nulami. K tomu je vhodné nejprve přehodit poslední dva řádky, abychom mohli použít k vytváření nul jedničku. \[ \left( \begin{array}{cccc|c} 1& 2& 2& 1& 0\\ 0& 1& -2& 1& 2\\ 0& -3& -1& -3& 1 \end{array}\right) \]

Nyní provedeme potřebnou úpravu. První dva řádky opíšeme. Místo třetího řádku napíšeme jeho součet s trojnásobkem druhého řádku. \[ \left( \begin{array}{cccc|c} 1& 2& 2& 1& 0\\ 0& 1& -2& 1& 2\\ 0& 0& -7& 0& 7 \end{array}\right) \]

Nyní přepíšme do tvaru soustavy rovnic

\[ \begin{aligned} x_1+2x_2+2x_3+x_4&=0\\ x_2-2x_3+x_4&=2\\ -7x_3\phantom{+x_4}&=7 \end{aligned} \]

Z poslední rovnice máme snadno \(x_3=-1\). Tutho hodnotu použijeme ve druhé rovnici. Protože však máme pořád dvě neznámé, jednu z nich zvolíme za parametr. \[ \begin{aligned} x_2-2x_3+x_4&=2\\ x_2+2+x_4&=2\\ x_2+x_4&=0\\ x_4&=t\\ x_2&=-t \end{aligned} \] Vypočtené hodnoty dosadíme do první rovnice a určíme zbývající neznámou \(x_1\). \[ \begin{aligned} x_1+2x_2+2x_3+x_4&=0\\ x_1-2t-2+t&=0\\ x_1&=2+t \end{aligned} \] Řešení je \(x_1=2+t\), \(x_2=-t\), \(x_3=-1\), \(x_4=t\), kde \(t\) je libovolné reálné číslo. Vektorově (maticově) máme řešení ve tvaru \[ \begin{pmatrix} x_1\\x_2\\x_3\\x_4 \end{pmatrix} = \begin{pmatrix} 2+t\\-t\\-1\\t \end{pmatrix} = \begin{pmatrix} 2\\0\\-1\\0 \end{pmatrix} +t \begin{pmatrix} 1\\-1\\0\\1 \end{pmatrix} . \]

Gaussova-Seidelova iterační metoda

Gaussova-Seidelova iterační metoda je jakýsi mezikrok mezi Jacobiho iterační metodou a Gausovou eliminací. Postupujeme jako v Jacobiho metodě, ale všechny zpřesněné hodnoty použijeme okamžitě, když jsou k dispozici. Nikoliv až v další iteraci jako u Jacobiho metody. Metoda konverguje za stejných podmínek jako Jacobiho metoda, ale rychleji a přesto nevznikají vyšší nároky na výpočetní výkon.

Použijeme příklad z Wikipedie. Soustavu \[\begin{array}{rrrrl} 10x_1 &- x_2 &+ 2x_3 & & = 6, \\ -x_1 &+ 11x_2 &- x_3 &+ 3x_4 & = 25, \\ 2x_1 &- x_2 &+ 10x_3 &- x_4 & = -11, \\ & 3x_2 &- x_3 &+ 8x_4 & = 15. \end{array}\] s diagonálně dominantní maticí převedeme na iterační tvar \[ \begin{aligned} x_1 & = x_2/10 - x_3/5 + 3/5, \\ x_2 & = x_1/11 + x_3/11 - 3x_4/11 + 25/11, \\ x_3 & = -x_1/5 + x_2/10 + x_4/10 - 11/10, \\ x_4 & = -3x_2/8 + x_3/8 + 15/8. \end{aligned} \] Poté vyjdeme z počátečního odhadu řešení a dosazujeme do pravých stran.

U Jacobiho metody pro počáteční odhad vypočteme nejprve všechny pravé strany a dosadíme do proměnných na levé straně jako zpřesnění počáteční aproximace. Tento postup opakujeme.

U Gaussovy-Seidlovy metody nejprve pomocí počátečního odhadu vypočteme z první rovnice \(x_1\) a tuto hodnotu ihned použijeme při výpočtu \(x_2\) z další rovnice. Obojí, \(x_1\) i \(x_2\) už využijeme při výpočtu \(x_3\) a tak dále. Po výpočtu \(x_4\) je první iterace dokončena a postup opět opakujeme, dokud dvě po sobě jdoucí iterace nejsou dostatečně blízké.

S nulovou počáteční aproximací dostáváme v prvním průchodu \[ \begin{aligned} x_1 & = 3/5 = 0.6, \\ x_2 & = 0.6/11 + 25/11 = 2.3272, \\ x_3 & = -0.6/5 +(2.3272)/10-11/10 = -0.9873,\\ x_4 & = -3(2.3272)/8 +(-0.9873)/8+15/8 = 0.8789. \end{aligned} \] Jak vidno, vypočtenou hodnotu \(x_1\) ihned použijeme pro výpočet \(x_2\). Obě tyto hodnoty ihned použijeme pro výpočet \(x_3\) a tak dále. V dalších iteracích postup opakujeme. Mimo jiné hodnoty v paměti přímo přepisujeme a nemusíme držet v paměti starou a novou hodnotu.

Pootočení souřadnic v rovině

Soustava s čárkovanými souřadnicemi \((x',y')\) je pootočena o úhel \(\theta\) oproti soustavě \((x,y)\).

V inženýrských problémech je častou aplikací lineární algebry transformace úlohy do vhodných souřadnic, ve kterých je popis jednodušší. Zpravidla se jedná o prosté otočení. Toto se používá při studiu dřeva, které má anatomicky význačné směry, při studiu vrstvených materiálů, při studiu chování vodorovně uložených geologických vrstev. Nemusí však vždy jít jenom o materiál s charakteristickými směry. Transformace mezi souřadnicemi se používá například v letectví, kdy je jedna souřadná soustava spojena s trupem a další dvě jsou pootočené ve směru křídel šípovitě připojených k trupu.

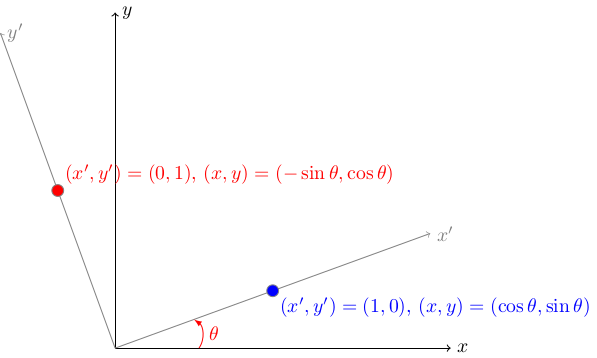
Je-li v rovině dána souřadná soustava \((x,y)\) a soustava \((x',y')\) pootočená o úhel \(\theta\) proti směru hodinových ručiček je vztah mezi souřadnicemi popsán vztahem \[ \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} x'\\y' \end{pmatrix}. \] To je možné zkontrolovat podle obrázku a souřadnic dvou bodů \((x',y')=(1,0)\) a \((x',y')=(0,1).\) Pro další body roviny to poté funguje automaticky.

Matici transformace budeme zkráceně označovat \(R\), pokud budeme potřebovat zdůraznit velikost úhlu, použijeme \(R(\theta)\) a pokud budeme potřebovat matici rozepsat ve složkách, budeme zkracovat výrazy \(\cos\theta\) a \(\sin\theta\) na \(C\) a \(S\) a psát \[R= \begin{pmatrix} C & -S \\ S & C \end{pmatrix}. \]

V minulé přednášce jsme viděli, že je-li \(A\) matice zobrazení v souřadnicích \((x,y)\), v souřadnicích \((x',y')\) má zobrazení vyjádření \(R^{-1}AR,\) kde \(R^{-1}=R(-\theta)= \begin{pmatrix} C&S\\-S&C \end{pmatrix}\) je matice pootočení v opačném směru. Stejným způsobem se transformují i tenzory.

Úloha na transformaci tenzoru napětí do anatomických směrů dřeva. Znázorněná krychlička je jenom reprezentující element většího tělesa. Zdroj: A. Požgaj a kol., Štruktúra a vlastnosti drevá.

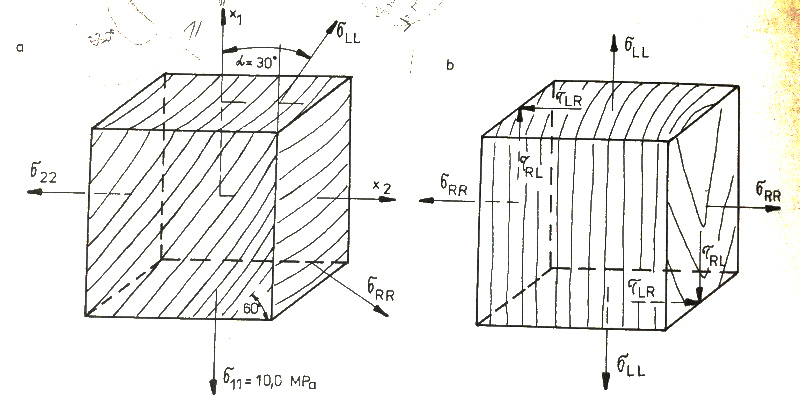
V knize A. Požgaj a kol., Štruktúra a vlastnosti dreva je následující úloha. Dřevo v konfiguraci podle obrázku je namáháno pouze tahovou silou svisle, tedy tenzor napětí má jenom jednu nenulovou složku. Naším cílem je pootočit souřadnou soustavu tak, aby byl tenzor napětí vyjádřen v anatomických směrech dřeva. Úloha je v knize vyřešena pomocí směrových kosinů. Ukážeme si alternativní způsob, který je výhodný v tom, že využívá pouze základní aparát lineární algebry. Původní souřadnice \((x_1,x_2)\) označíme \((x,y)\), osa \(x\) směřuje vodorovně vpravo (v obrázku \(x_2\)) a osa \(y\) nahoru (v obrázku \(x_1\)). Tenzor napětí je \(A= \begin{pmatrix} 0 & 0\\0& 10 \end{pmatrix}\) (tah pouze ve směru osy \(y\)). Souřadnice je nutno pootočit o \(30\) stupňů po směru hodinových ručiček, tj. v záporném směru. Nový tenzor napětí je \[R(30^\circ)AR(-30^\circ)= \begin{pmatrix} 2.5 & -4.3\\ -4.3& 7.5 \end{pmatrix}.\] V nových souřadnicích je směr \(x'\) radiální a proto \(\sigma_{RR}=2.5\) a \(\sigma_{LL}=7.5\). Mimodiagonální složka udává komponentu \(\sigma_{RL}=-4.3\). Tento výsledek je stejný, jako výsledek získaný jiným postupem v knize. Použili jsme však jenom základní nástroje lineární algebry.

Transformace tenzoru

Schopnost transformovat tenzory napětí nebo deformace je důležitá u studia vrstvených materiálů. Na obrázku Jatawood, pro výrobu rukojetí nožů. Zdroj: jatagan.eu

Úloha na transformaci tenzoru, kterou jsme řešili na minulém slidu je v aplikacích velmi důležitá. Proto existuje řada grafických nebo inženýrských metod na řešení tohoto úkolu. Tyto metody jsou důvtipné a názorné, například metoda Mohrovy kružnice, oproti lineární algebře však mají zásadní nevýhodu: uživatel se musí stále učit něco nového a dostává návod "jak", nikoliv "proč". Použitím aparátu lineární algebry, stejně jako dokážeme v pootočených souřadnicích vyjádřit libovolné zobrazení, dokážeme vyjádřit v pootočených souřadnicích i libovolný tenzor. Vzorce jsou stejné a navíc při otočení v rovině je matice rotace ortogonální, tj. inverzní matice je maticí transponovanou. Pro symetrický tenzor \(A= \begin{pmatrix} a_{11} & a_{12} \\ a_{12} & a_{22} \end{pmatrix}\) dostáváme v souřadnicích otočených o úhel \(\theta\) proti směru hodinových ručiček \[\begin{pmatrix} a'_{11} & a'_{12} \\ a'_{12} & a'_{22} \end{pmatrix} = \begin{pmatrix} C&S\\-S&C \end{pmatrix} \begin{pmatrix} a_{11} & a_{12} \\ a_{12} & a_{22} \end{pmatrix} \begin{pmatrix} C&-S\\S&C \end{pmatrix}, \] kde po výpočtu \[ \begin{aligned} a'_{11}&=C^2a_{11} + S^2a_{22} + 2CSa_{12},\\ a'_{22}&=S^2a_{11} + C^2a_{22} - 2CSa_{12},\\ a'_{12}&=-CSa_{11} + CSa_{22} + (C^2 - S^2)a_{12}. \end{aligned}\tag{*} \] Tento vztah je lineání vzhledem ke všem komponentám a je možné jej zapsat pomocí maticového násobení \[ \begin{pmatrix} a'_{11}\\a'_{22}\\a'_{12} \end{pmatrix} = \begin{pmatrix} C^2 & S^2 & 2CS\\ S^2 & C^2 & -2CS\\ -CS & CS & C^2-S^2 \end{pmatrix} \begin{pmatrix} a_{11}\\a_{22}\\a_{12} \end{pmatrix}. \] Tento vztah je uveden i v literatuře A. Požgaj a kol., Štruktúra a vlastnosti drevá a v e-opoře Fyzikální a mechanické vlastnosti dřeva. Zde je také uvedena jedna z aplikací, transformace tenzoru deformací naměřených při bobtnání dřeva. V této úloze je nutno tenzor deformací transformovat do anatomických směrů dřeva. To je možné udělat po změření sklonu vláken a pootočení tenzoru o příslušný úhel.

Inverzní operací je pootočení o úhel \(-\theta\) a proto je snadné najít inverzní transformaci: vzhledem k sudosti funkce \(\cos\) a lichosti funkce \(\sin\) stačí změnit znaménko u členů s \(S\), tj. \[ \begin{pmatrix} a_{11}\\a_{22}\\a_{12} \end{pmatrix} = \begin{pmatrix} C^2 & S^2 & -2CS\\ S^2 & C^2 & 2CS\\ CS & -CS & C^2-S^2 \end{pmatrix} \begin{pmatrix} a'_{11}\\a'_{22}\\a'_{12} \end{pmatrix}. \]

Poznámka. Pokud vypočteme derivaci členů \(a'_{11}\) a \(a'_{22}\) podle \(\theta\), dostaneme použitím \[\frac{\mathrm d}{\mathrm d\theta}C^2=\frac{\mathrm d}{\mathrm d\theta}\cos^2\theta=2\cos\theta(-\sin\theta)=-2CS,\] a analogicky \(\frac{\mathrm d}{\mathrm d\theta}S^2=2SC\), \(\frac{\mathrm d}{\mathrm d\theta}CS=-S^2+C^2\) derivace \[ \begin{aligned} \frac{\mathrm d a'_{11}}{\mathrm d\theta}&= -2CSa_{11}+2SCa_{22}+2(C^2-S^2)a_{12}=2a'_{12},\\ \frac{\mathrm d a'_{22}}{\mathrm d\theta}&= 2SCa_{11}-2CSa_{22}+2(S^2-C^2)a_{12}=-2a'_{12}.\\ \end{aligned} \] To znamená, že lokální extrémy diagonálních prvků nastávají v okamžiku, kdy jsou prvky mimo diagonálu nulové. Toto pozorování perfektně ladí s výsledky, které známe v lineární algebře i bez hledání lokálních extrémů a bez derivací. Náznak tohoto konceptu si představíme na dalších stránkách. Budeme potřebovat připomenout definici vlastních vektorů.

Pozor. V případě tenzoru deformace se někdy se namísto mimodiagonální komponenty bere její dvojnásobek, protože ten má názorný význam jako úhel smyku. Proto se někdy v literatuře uvádí transformační vzorec pro deformace v upraveném tvaru, kdy u složek se součinem \(CS\) ve třetím sloupci není koeficient \(2\) a u odpovídajících složek ve třetím řádku tento koeficient naopak figuruje. Je proto potřeba dávat pozor na to, s jakými komponentami je tenzor malých deformací uvažován.

Role vlastních vektorů při transformaci matic

Eigenvectors (red) do not change direction when a linear transformation (e.g. scaling) is applied to them. Other vectors (yellow) do. Zdroj: http://www.visiondummy.com.

Budeme zkoumat, kdy platí \[P^{-1}AP=D\] pro čtvercové matice \(P\), \(A\) a diagonální čtvercovou matici \(D\). Vynásobením maticí \(P\) zleva dostaneme \[AP=PD.\] Ve cvičení jsme násobili čtvercovou matici s maticí diagonální a není těžké vidět obecný princip, že matice \(PD\) má za sloupce násobky sloupců matice \(P\) s odpovídajícím číslem z hlavní diagonály matice \(D\). Například pro první sloupec matice \(P\) a první číslo v hlavní diagonále matice \(D\), které označíme \(\vec p_1\) a \(\lambda_1\), dostáváme \[A\vec p_1=\lambda_1p_1,\] tj. (viz předchozí přednášky) \(p_1\) je vlastní vektor matice \(A\) příslušný vlastní hodnotě \(\lambda_1\). Podobný princip platí pro všechny sloupce. Je otázkou, jestli vlastních hodnot a vlastních vektorů je tolik, kolik pro diagonalizaci "potřebujeme". Částečně pozitivní odpověď na tuto otázku udávají věty na následujícím slidu.

Transformace symetrické matice na diagonální tvar

Věta (vlastní čísla symetrické matice).

Symetrická čtvercová matice \(A\) řádu \(n\) má \(n\) reálných vlastních čísel (počítáno i s případnou násobností).

Věta (diagonalizace symetrické matice).

Nechť má symetrická čtvercová matice \(A\) řádu \(n\) celkem \(n\) reálných různých vlastních čísel \(\lambda_i\). Označme odpovídající vlastní vektory jednotkové délky \(\vec v_i\).

• Matice \(P\) sestavená tak, že sloupce této matice jsou tvořeny vektory \(\vec v_i\) je ortogonální.
• Matice \(D\) definovaná vztahem \[D=P^TAP\] je diagonální.
• Diagonální prvky matice \(D\) jsou právě vlastní čísla \(\lambda_i\) a jsou ve stejném pořadí jako odpovídající vlastní vektory v matici \(P\).

Pokud je tenzor spojený s materiálovou chrakteristikou v diagonálním tvaru, redukuje se složitost problému. Podobná redukce složitosti je i při jiných příležotostech, například při skládání Rubikovy kostky pomocí metody Human Thistlethwaite Algorithm. V této metodě se úloha nejprve redukuje na jednodušší úlohu, kdy každá barva je buď ve svojí straně nebo protilehlé. Tak je možné složit kostku buď bez nepříjemného učení se umělých algoritmů (člověk), nebo do 20 tahů (stroj a nejlepší lidé).

Matice transformace \(P\) z předchozí věty je ortogonální (její transponovaná matice je současně její inverzní matice) a její determinant je roven \(1\) nebo \(-1\). Pokud je determinant kladný, reprezentuje matice pootočení soustavy souřadnic. Pokud je determinant záporný, jedná se o pootočení spojené se zrcadlením jedné osy. Protože tento případ většinou z fyzikálních důvodů nepreferujeme, sestavujeme matici transformace tak, aby měla determinant kladný. V případě záporného determinantu stačí prohodit dva vektory (sloupce matice transformace) mezi sebou, nebo jeden vynásobit faktorem \(-1\).

Pro kontrolu je zajímavé vědět, že determinant matice se pootočením nemění a je tedy stejný pro původní i transformovanou matici. Totéž platí pro součet prvků v hlavní diagonále (v lineární algebře se nazývá stopa matice), pro charakteristický polynom a pro vlastní hodnoty. Tenzor, jak jej uvažujeme v tomto textu, je matice, která má navíc fyzikální význam a vzhledem ke své povaze pro ni platí speciální transformační pravidla. Nicméně je to mimo jiné i matice a proto vše výše uvedené platí i pro tenzory.

Ve videu https://www.youtube.com/watch?v=xdxVpC856ms je pomocí vzorců odvozován diagonální tvar tenzoru napětí \[A= \begin{pmatrix} 20 & 30 \\ 30 & -10 \end{pmatrix}. \] Ukážeme si řešení úlohy bez použití vzorců, jenom prostředky lineární algebry. Charakteristický polynom této matice je \[\det(A-\lambda I)= \begin{vmatrix} 20-\lambda & 30 \\ 30 & -10-\lambda \end{vmatrix}= (20-\lambda)(-10-\lambda)-30^2=\lambda^2-10\lambda-1100 \] s kořeny \(\lambda_1\approx 38.54\) a \(\lambda_2\approx -28.54\). To budou prvky v hlavní diagonále po transformaci tenzoru.

Pokud budeme chtít vědět, jak jsou nové osy orientovány vůči osám původním, musíme najít i vlastní vektory. Vlastní vektor příslušný hodnotě \(\lambda_1\) je řešením soustavy s maticí soustavy \[ A-\lambda_1 I\approx \begin{pmatrix} -18.54 & 30 \\ 30 & -48.54 \end{pmatrix} \] a nulami vpravo. Přibližným řešením je vektor \(\vec u_1= \begin{pmatrix} 30 \\ 18.54 \end{pmatrix}\). (Toto plyne z první rovnice, druhá rovnice musí být splněna automaticky, protože jsme použili vlastní hodnotu a soustava musí mít nenulové řešení. Nicméně výpočet je zatížen zaokrouhlovací chybou.) Po vydělení normou vektoru dostáváme \(\begin{pmatrix} 0.851 \\ 0.526 \end{pmatrix}\). Druhý vlastní vektor je kolmý, tj. \(\begin{pmatrix} -0.526 \\ 0.851 \end{pmatrix}\). Po transformaci maticí \(P= \begin{pmatrix} 0.851 & -0.526 \\ 0.526 & 0.851 \end{pmatrix}\) dostáváme (na dvě desetiná místa) \[P^{T}\begin{pmatrix} 20 & 30 \\ 30 & -10 \end{pmatrix} P=\begin{pmatrix} 38.54 & 0 \\ 0 & -28.54 \end{pmatrix}. \] To vlastně ani nemusíme počítat, věta v úvodu tohoto slidu zaručuje, že výsledná matice bude diagonální a bude obsahovat vlastní hodnoty. Z matice \(P\) vidíme sinus a kosinus úhlu pootočení a odsud určíme snadno, o kolik se souřadná soustava otáčí a v jakém směru.