
Tepelná výměna probíhá intenzivněji při velkém rozdílu teplot, https://pixabay.com
Obyčejná diferenciální rovnice je rovnice, kde vystupuje neznámá funkce a její derivace. Setkáváme se s ní například všude tam, kde rychlost růstu nebo poklesu veličiny souvisí s její velikostí. Například rychlost s jakou se mění teplota horkého tělesa je funkcí teploty samotné. Rychlost tepelné výměny mezi dvěma tělesy je totiž úměrná rozdílu jejich teplot (Newtonův zákon). Takto se přirozeně diferenciální rovnice objevují v modelech nejrůznějších dějů jevů. Podstatu děje, který modelujeme, musí dodat fyzika, biologie nebo jiná aplikovaná věda. To v matematice obsaženo není. Matematika poté poslouží k analýze, jaké jsou pozorovatelné důsledky a tím se ověří, jestli příslušná aplikovaná věda správně vystihuje podstatu modelovaného děje.
Definice (diferenciální rovnice).
Obyčejnou diferenciální rovnicí prvního řádu rozřešenou vzhledem k derivaci (stručněji též diferenciální rovnicí, DR) s neznámou \(y\) rozumíme rovnici tvaru \[ \frac{\mathrm{d}y}{\mathrm{d}x}=\varphi(x,y) \tag{1}\] kde \(\varphi\) je funkce dvou proměnných.
(anglicky ordinary differential equation, ODE)
Další formy zápisu rovnice (1) jsou \[y'=\varphi(x,y),\] \[{\mathrm{d}y}=\varphi(x,y)\mathrm{d}x,\] \[{\mathrm{d}y}-\varphi(x,y)\mathrm{d}x=0.\]
Příklad. Najděte všechny funkce splňující \(y'=2xy\). (Naučíme se řešit později.)
Diferenciální rovnice udává scénář vývoje systému. K jednoznačnému předpovězení budoucího stavu je ovšem nutno znát nejenom, jaký mechanismus ovlivňuje vývoj systému, ale také stav současný.
Definice (počáteční podmínka, Cauchyova úloha).
Nechť \(x_0\), \(y_0\) jsou reálná čísla. Úloha najít řešení rovnice
\[ \frac{\mathrm{d}y}{\mathrm{d}x}=\varphi(x,y), \tag{1}\] které splňuje zadanou počáteční podmínku \[ y(x_0)=y_0 \tag{2}\] se nazývá počáteční (též Cauchyova) úloha.Řešení Cauchyovy úlohy nazýváme též partikulárním řešením rovnice. Graf libovolného partikulárního řešení se nazývá integrální křivka.
(anglicky initial condition, IC, initial value problem, IVP)
Příklad. Najděte všechny funkce splňující \(y'=2xy\) a \(y(0)=3\). (Naučíme se řešit později.)
Věta (existence a jednoznačnost řešení Cauchyovy úlohy).
Má-li funkce \(\varphi (x,y)\) ohraničenou parciální derivaci \(\frac{\partial \varphi}{\partial y}\) v okolí počáteční podmínky, potom má počáteční úloha (1)-(2) právě jedno řešení definované v nějakém okolí počáteční podmínky.
Příklad. Rovnice \[y'=y\tag{3}\] má řešení \(y=e^x\), což nahlédneme snadno, protože exponenciální funkce se nemění derivováním. Dosazením je možné ukázat, že má dokonce řešení \[y=Ce^x,\tag{4}\] kde \(C\) je libovolné číslo.
Příklad. Řešení počáteční úlohy \[y'=y, \quad y(x_0)=y_0\] najdeme tak, že využijeme řešení (4) a zařídíme, aby byla splněna počáteční podmínka. Tj. řešením počáteční úlohy je \[y= (y_0 e^{-x_0}) e^x.\] Vidíme, že toto řešení existuje pro každou počáteční podmínku a proto vzorec (4) popisuje dokonce všechna řešení rovnice (3).
Řešení diferenciální rovnice je nekonečně mnoho. Zpravidla je dokážeme zapsat pomocí jediného vzorce, který obsahuje nějakou (alespoň do jisté míry libovolnou) konstantu \(C\). Takový vzorec se nazývá obecné řešení rovnice. Pokud není zadána počáteční podmínka a mluvíme o partikulárním řešení, máme tím na mysli jednu libovolnou funkci splňující diferenciální rovnici.
Příklad: Obecným řešením diferenciální rovnice \[y'=2xy\] je \[y=Ce^{x^2}, \quad C\in\mathbb{R}.\] Žádná jiná řešení neexistují, všechna řešení se dají zapsat v tomto tvaru pro nějakou vhodnou konstantu \(C\). Partikulárním řešením je například \(y=5e^{x^2}\). Řešením počáteční úlohy \[y'=2xy, \quad y(0)=3\] je \[y=3e^{x^2}.\]
Online řešiče ODE (symbolicky):

Tepelná výměna probíhá intenzivněji při velkém rozdílu teplot, https://pixabay.com

Rovnice konstantního růstu nebo úbytku je základem datování pomocí uhlíku, https://www.flickr.com/photos/capturetheuncapturable, licence CC BY 2.0

Jezero, ve kterém se přirozeně obměňuje znečištěná voda za čistou, se dokáže samo zotavit ze znečištění. Rychlost vyplavování nečistot je úměrná míře znečištění. https://pixabay.com
Při operaci ztrácí pacient krvinky rychlostí úměrnou koncentraci krvinek. Pokud je tato koncentrace malá, pacient ztratí krvinek málo. Zdroj: https://pixabay.com

Při intenzivním lovu může dojít ke zničení populace https://pixabay.com

Tři dosud nalezené meteority Benešov. foto: Pavel Spurný, převzato z https://dvojka.rozhlas.cz/
Česká republika je na světové špičce ve oblasti propočítávání dráhy meteoritů ze světelné stopy zachycené sítí bolidových kamer. Vědcům z Astronomického ústavu se podařilo
Meteority s vystopovaným původem jsou extrémně vzácné (do roku 2000 jenom 5 meteoritů, do roku 2016 pouze 31 meteoritů) a tým založený Zdeňkem Ceplechou a nyní vedený Pavlem Spurným se podílel na výpočtu drah většiny z nich. Použité metody jsou popsány například v článku Ceplecha, Revelle: Fragmentation model of meteoroid motion, mass loss, and radiation in the atmosphere, Meteoritics & Planetary Science 40, Nr 1, 35–54 (2005). Například ztráta rychlosti třením v atmosféře je modelována rovnicí \[\frac{\mathrm dv}{\mathrm dt}=-K\rho m^{-1/3}v^{2}\] a ztráta hmotnosti vypařováním \[\frac{\mathrm dm}{\mathrm dt}=-K\sigma \rho m^{2/3}v^3.\] Jedná se o diferenciální rovnice, kde zrychlení (derivace rychlosti) a časová změna hmotnosti (derivace hmotnosti podle času, rychlost, s jakou ubývá hmotnost) je úměrná vhodným mocninám těchto veličin.
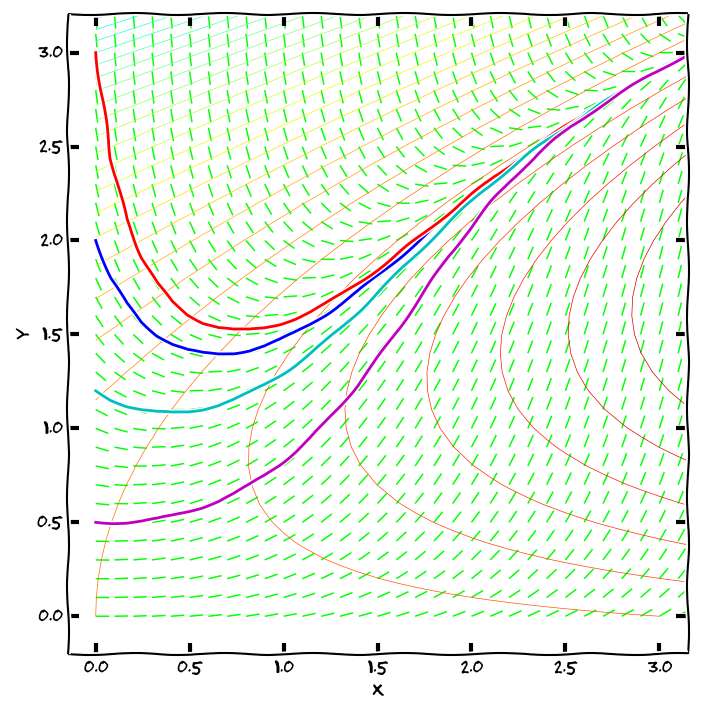
Směrové pole diferenciálni rovnice, integrální křivky, isokliny
Protože derivace funkce v bodě udává směrnici tečny ke grafu funkce v tomto bodě, lze rovnici \[\frac{\mathrm dy}{\mathrm dx}=\varphi(x,y)\tag{1}\] chápat jako předpis, který každému bodu v rovině přiřadí směrnici tečny k integrální křivce, která tímto bodem prochází. Sestrojíme-li v dostatečném počtu (například i náhodně zvolených) bodů \([x,y]\) v rovině vektory \((1,\varphi(x,y))\), obdržíme směrové pole diferenciální rovnice — systém lineárních elementů, které jsou tečné k integrálním křivkám.
Počáteční podmínka \(y(x_0)=y_0\) geometricky vyjadřuje skutečnost, že graf příslušného řešení prochází v rovině bodem \([x_0,y_0]\). Má-li tato počáteční úloha jediné řešení, neprochází bodem \([x_0,y_0]\) žádná další křivka. Má-li každá počáteční úloha jediné řešení (což bude pro nás velice častý případ), znamená to, že integrální křivky se nikde neprotínají.
Křivky s konstantní hodnotou \(\varphi(x,y)\) mají tu vlastnost, že je všechna řešení protínají pod stejným úhlem, měřeným od kladné části osy \(x\). Například v bodech kde platí \(\varphi(x,y)=0\) míří všechny integrální křivky vodorovně. Proto se křivky, kde je \(\varphi(x,y)\) konstantní, nazývají izokliny.

Letecký snímek údolí Vajont krátce po katastrofě. Video ukazuje, že při modelování procesu ve zmenšeném měřítku je nutné transformovat ostatní veličiny, například čas. Pro nás klíčová slova v čase 39:21 dokumentu jsou "v přepočtu pro simulaci se jedná o zhruba čtyři sekundy". Čas ve zmenšeném modelu ubíhá jinou rychlostí než čas v reálném ději. Foto: Wikipedia.
Naučíme se vyjadřovat diferenciální rovnici v jiných proměnných tak, aby bylo možné snížit počet parametrů v této rovnici. Pro jednoduchost budeme uvažovat jenom případ, kdy nová proměnný je lineární funkcí původní proměnné.
Uvažujme funkci \(y\) proměnné \(x\). Připomeneme si vzorce pro derivaci součtu, derivaci konstantního násobku a derivaci složené funkce, ale uvedeme si je v kontextu vhodném pro studium diferenciálních rovnic.
Výše uvedené výpočty je možno shrnout do pravidla v následující poznámce.
Poznámka (transformace diferenciální rovnice do jiných jednotek).
Pro \(Y=k_1(y-y_0)\) a \(X=k_2 x\) platí \[ \frac{\mathrm d Y}{\mathrm d X} = \frac{\mathrm d \Bigl(k_1(y-y_0)\Bigr)}{\mathrm d (k_2 x)} = \frac{k_1}{k_2} \frac{\mathrm dy}{\mathrm dx}\] a podobně (všimněte si druhé mocniny u \(k_2\) díky druhé derivaci) \[ \frac{\mathrm d^2 Y}{\mathrm d X^2} = \frac{k_1}{k_2^2} \frac{\mathrm d^2y}{\mathrm dx^2}.\] Výraz nalevo neobsahuje konstanty, které jsou ve výrazu napravo. Tyto konstanty jsou v definici nových veličin \(X\) a \(Y\).
Navíc vzorec z poznámky silně připomíná klasické počítání se zlomky. Proto máme Leibnizův tvar zápisu derivací \(\frac{\mathrm dy}{\mathrm dx}\) při studiu diferenciálních rovnic více v oblibě, než zápis Lagrangeův, \(y'\).
Příklad. Diferenciální rovnice tepelné výměny \[\frac{\mathrm dT}{\mathrm dt}=-k(T-T_\infty), \quad T(0)=T_0\tag{*}\] obsahuje tři parametry: teplotu okolního protředí \(T_\infty\), počáteční teplotu \(T_0\) a konstantu \(k\) související s fyzikálními vlastnostmi prostředí. Postupně můžeme posunout teplotní stupnici tak, aby teplota okolí byla nula a počáteční teplota jedna, tj. hodnotu \(T\) snížíme o \(T_\infty\) a upravíme dílek stupnice \((T_0-T_\infty)\)-krát \[\frac{\mathrm d\left(\frac{T-T_\infty}{T_0-T_\infty}\right)}{\mathrm dt}=-k\frac{T-T_\infty}{T_0-T_\infty}\] vydělit konstantou \(k\) \[\frac{\mathrm d\left(\frac{T-T_\infty}{T_0-T_\infty}\right)}{k\mathrm dt}=-\frac{T-T_\infty}{T_0-T_\infty}\] a přeškálovat pomocí konstanty \(k\) čas \[\frac{\mathrm d\left(\frac{T-T_\infty}{T_0-T_\infty}\right)}{\mathrm d(kt)}=-\frac{T-T_\infty}{T_0-T_\infty}.\] Po substituci \(y=\frac{T-T_\infty}{T_0-T_\infty}\), \(x=kt\) má úloha tvar \[\frac{\mathrm d y}{\mathrm d x}=-y,\quad y(0)=1. \tag{**}\] Nová rovnice (**) neobsahuje žádné parametry a proto je pro studium jednodušší. Přesto je v ní obsažena veškerá informace obsažená v rovnici (*). Tuto informaci je však nutno interpretovat v kontextu definice nových proměnných. Například to, že všechna řešení rovnice (**) konvergují k nule znamená, že všechna řešení rovnice (*) konvergují k \(T_0\). To, že řešení rovnice (**) klesne na poloviční hodnotu za čas \(\ln 2\) znamená, že vzdálenost řešení rovnice (*) od rovnovážného stavu se na polovinu zmenší za čas \(\frac 1k \ln 2\).
Poznámka (nondimenzinalizace, rozměrová analýza).
Proces eliminace parametrů z modelu popsaného diferenciální rovnicí se nazývá nondimenzionalizace nebo rozměrová analýza modelu, protože eliminaci parametrů je vhodné provádět tak, aby výsledné nové veličiny vycházely bez fyzikálních jednotek. K tomu se provádí rozbor jednotek jednotlivých veličin. V jednoduchých případech však stačí primitivní postup popsaný v odstavcích výše a ukázaný na příkladu. V tomto příkladě veličina \(x\) nemá fyzikální jednotku, protože je součinem konstanty \(k\) (s jednotkou \(\mathrm s^{-1}\)) a času \(t\) (s jednotkou \(\mathrm s\)). Je možné ji považovat za bezrozměrný čas. Veličina \(y\) také nemá fyzikální jednotku, protože je podílem dvou teplot a je možné ji považovat za bezrozměrnou teplotu.
V této úloze bylo zavedení nových veličin přirozené. I u méně zřejmých úloh zkušenosti ukazují, že je vhodné volit transformaci tak, aby vznikly veličiny bezrozměrné, které nemají fyzikální jednotku. Například v Horáček, Fyzikální a mechanické vlastnosti dřeva I je zavedena bezrozměrná vlhkost, bezrozměrný čas a bezrozměrná vzdálenost na straně 61 pro rovnici popisující difuzi a charakteristická délka, Biotovo číslo (bezrozměrná tepelná vodivost) a bezrozměrná teplota, bezrozměrný čas a bezrozměrná vzdálenost pro rovnici popisující vedení tepla na stranách 88 a 89.
Rovnice \[\frac{\mathrm dy}{\mathrm dx}=f(y)\tag{♣}\] se nazývá autonomní, nebo též nezávislá na čase. Je speciálním případem rovnice se separovanými proměnnými, která je uvedena na dalším slidu a naučíme se ji řešit analytickou cestou. Proto se nyní nebudeme zaměřovat na hledání obecného řešení, ale pokusíme se popsat chování řešení, aniž bychom tato řešení znali. Pokusíme se s co nejmenší námahou říct, jak se budou řešení chovat.
Věta (stabilita konstantních řešení).
Jestliže platí \(f(y_0)=0\), je konstantní funkce \(y(x)=y_0\) konstantním řešením rovnice \[\frac{\mathrm dy}{\mathrm dx}=f(y).\] Toto řešení je stabilní pokud \(\frac{\mathrm df}{\mathrm dx}(y_0)<0\) a nestabilní pokud \(\frac{\mathrm df}{\mathrm dx}(y_0)>0\).
Pro grafickou intepretaci je vhodné připomenout, že funkce s kladnou derivací jsou rostoucí a funkce se zápornou derivací klesající. Pokud má tedy pravá strana derivaci různou od nuly, poznáme stabilitu z monotonie pravé strany.
Příklad. Logistická diferenciální rovnice s konstantním lovem \(h\), tj. rovnice \[\frac{\mathrm dy}{\mathrm dt}=ry\left(1-\frac yK\right)-h,\] má pro malé \(h\) dva stacionární body. Funkce \(ry\left(1-\frac yK\right)\) je parabola otočená vrcholem nahoru a s nulovými body \(y=0\) a \(y=K\). V prvním stacionárním bodě je funkce rostoucí a tento stacionární bod je nestabilní. Ve druhém stacionárním bodě je funkce klesající a tento stacionární bod je stabilní. Jak se zvyšuje faktor \(h\), graf paraboly se posouvá směrem dolů a oba stacionární body se posouvají směrem k sobě a k vrcholu. Jejich stabilita zůstává neporušena. To znamená, že sice pořád existuje stabilní stav, ale se zvyšující se intenzitou lovu se tento stacionární stav dostává stále blíže ke stavu nestacionárnímu a rovnováha je tedy poněkud křehká.
Definice (ODE se separovanými proměnnými).
Diferenciální rovnice tvaru \[ \frac{\mathrm dy}{\mathrm dx}=f(x)g(y) \tag{S}\] kde \(f\) a \(g\) jsou funkce spojité na (nějakých) otevřených intervalech se nazývá obyčejná diferenciální rovnice se separovanými proměnnými.
Příklad: Rovnice \[y'+xy +xy^2=0\] je rovnicí se separovanými proměnnými, protože je možno ji zapsat ve tvaru \[y'=-xy(y+1).\] Rovnice \[y'=x^2-y^2\] není rovnice se separovatelnými proměnnými.
Má-li algebraická rovnice \(g(y)=0\) řešení \(k_1\), \(k_2\), …, \(k_n\), jsou konstantní funkce \(y\equiv k_1\), \(y\equiv k_2\), …, \(y\equiv k_n\) řešeními rovnice.
Pracujme na intervalech, kde \(g(y)\neq 0\) a odseparujeme proměnné. \[ \frac{\mathrm{d}y}{g(y)}=f(x)\mathrm{d}x\]
Získanou rovnost integrujeme. Tím získáme obecné řešení v implicitním tvaru. \[ \int \frac{\mathrm{d}y}{g(y)}=\int f(x)\mathrm{d}x+C\]
Pokud je zadána počáteční podmínka, je možné ji na tomto místě dosadit do obecného řešení a určit hodnotu konstanty \(C\). Tuto hodnotu poté dosadíme zpět do obecného řešení a obdržíme řešení partikulární.
Pokud je to možné, převedeme řešení (obecné nebo partikulární) do explicitního tvaru (vyjádříme odsud \(y\)).
Poslední krok (převod do explicitního tvaru) je volitelný, zpravidla záleží na tom, co dalšího hodláme s řešením dělat. Pro většinu výpočtů je však explicitní tvar vhodnější než tvar implicitní a proto se o něj vždy snažíme.
Poznámka (zápis partikulárního řešení pomocí určitého integrálu).
V případě počáteční podmínky \(y(x_0) = y_0\) je možné spojit třetí a čtvrtý krok a použít určitý integrál \[ \int_{y_0}^y \frac{\mathrm{d}t}{g(t)}=\int_{x_0}^x f(t)\mathrm{d}t. \]
Počáteční úloha má jediné řešení, pokud má pravá strana ohraničenou parciální derivace podle \(y\), jak je zmíněno v úvodu přednášky. Nicméně pro diferenciální rovnici se separovanými proměnnými je možné vyslovit následující mnohem jednodušší postačující podmínku pro jednoznačnost řešení.
Věta (existence a jednoznačnost řešení Cauchyovy úlohy pro rovnici se separovanými proměnnými).
Je-li \(g(y_0)\neq 0\), má počáteční úloha \[\frac{\mathrm dy}{\mathrm dx}=f(x)g(y),\qquad y(x_0)=y_0\] právě jedno řešení definované v nějakém okolí počáteční podmínky.

Londýnská mlha. Dnes už to není jako za časů Sherloka Holmese. Poslední velká mlha (Pea soup fog) byla v roce 1952. Zdroj: Wikipedia.
Modelujme růst kulové kapky. Ta roste tak, že na povrchu kondenzují vodní páry. Kapka proto roste tak, že její objem se zvětšuje rychlostí úměrnou povrchu. Povrch je zase úměrný druhé mocnině poloměru a poloměr je úměrný třetí odmocnině objemu. Platí tedy (po sloučení všech konstant úměrnosti do jedné) \[\frac{\mathrm dV}{\mathrm dt}=kV^{2/3}.\]
Tato rovnice má konstantní řešení \(V=0\). Nekonstantní řešení dostaneme po úpravě \[V^{-2/3}\mathrm dV=k\mathrm dt\] a po integraci \[\int V^{-2/3}\mathrm dV=k\int \mathrm dt,\] což dává \[3V^{1/3}=kt+C\] a \[V=\left(\frac 13 kt+ \frac 13 C\right)^3,\] tj. \[V=\left(k_0t+ c\right)^3,\] kde \(k_0=\frac 13 k\) a \(c=\frac 13 C\) jsou konstanta spojená rychlostí kondenzace a integrační konstanta.
Všimněte si, že počáteční úloha s počáteční podmínkou \(V(0)=0\) má konstantní nulové řešení \[V(t)=0\] a nenulové řešení \[V(t)=(k_0t)^3.\] Máme zde tedy nejednoznačnost v řešení počáteční úlohy. Tato nejednoznačnost není v rozporu s větou o existenci a jednoznačnosti řešení, protože pravá strana je nulová (podmínka pro separovatelnou rovnici není splněna) a nemá ohraničenou derivaci podle \(V\) (podmínka pro obecnou rovnici také není splněna). A nejednoznačnost má v tomto případě dokonce fyzikální význam. Plynné skupenství může existovat i pod bodem kondenzace. Takovému jevu se říká přechlazená pára. Aby došlo ke kondenzaci, musí být k dispozici kondenzační jádra, například nečistoty ve vzduchu. Proto ve znečištěném ovzduší dochází častěji ke kondenzaci a tvorbě mlhy. Své by o tom mohli vyprávět obyvatelé Londýna, kteří se proslulých mlh zbavili poté, co se omezilo topení uhlím. My dnes spíše známe přechlazenou tekutinu ve formě hřejících polštářků, kde se po lupnutí plíškem spustí přeměna skupenství na pevné spojená s intenzivním uvolněním tepla.

Téměř veškerá klasická mechanika a dynamika pohybů se redukuje na studium diferenciálních rovnic druhého řádu. Ve vesmíru i na Zemi. Zdroj: pixabay.com.
Je-li \(x\) poloha tělesa, je derivace \(\frac{\mathrm dx}{\mathrm dt}\) rychlost a druhá derivace \(\frac{\mathrm d^2x}{\mathrm dt^2}\) zrychlení. Podle Newtonova pohybového zákona je součin hmotnosti a zrychlení roven výsledné působící síle. Tato síla může mít složku závislou na poloze (například síla, která vrací těleso do rovnovážné polohy), složku závislou na rychlosti (odporová síla prostředí) a složku nezávislou na poloze i rychlosti (například vnější síla). Proto je přirozené v podstatě jakýkoliv pohyb v mechanice modelovat pomocí diferenciální rovnice druhého řádu \[m \frac{\mathrm d^2x}{\mathrm dt^2} = - kx - b \frac{\mathrm dx}{\mathrm dt} + F.\] Přirozeně přitom formulujeme počáteční podmínky pro počáteční polohu a počáteční rychlost, tj. \(x(t_0)=x_0\), \(\frac{\mathrm dx}{\mathrm dt}(t_0)=x_1\). Každá počáteční úloha má právě jedno řešení. Taková úloha se zpravidla řeší podobně jako u diferenciálních rovnic prvního řádu: najde se obecné řešení a poté se ze všech funkcí, které splňují danou diferenciální rovnici, vybere ta jediná, která splňuje i počáteční podmínky. Numerický výpočet se děje podobně jako u rovnice prvního řádu: řešení se prodlužuje po malých krocích a v rámci každého kroku aproximujeme pohyb rovnoměrným pohybem. (Film Hidden figures a hlavní hrdinka propočítávající dráhu pro návrat prvního amerického astronauta.)
Při studiu deformací nosníků nebo kmitů strun, ploch či těles se setkáme s diferenciálními rovnicemi typů \[\frac{\mathrm d^2x}{\mathrm dt^2} + kx = q \] a \[\frac{\mathrm d^4x}{\mathrm dt^4} = q. \] U takových úloh definujeme podmínky ve dvou různých bodech. Například u struny nebo u oboustranně vetknutého namáhaného nosníku je v bodech uchycení nulová výchylka a proto je přirozené formulovat okrajové podmínky \(x(0)=0\) a \(x(l)=0\). Řešení takové úlohy existuje jenom pro některé kombinace parametrů. Fyzikální rozbor ukazuje, že okrajová podmínka je to místo, kde se objeví efekt, že struna kmitá jenom na některých frekvencích (na základní frekvenci na kterou je naladěna a na vyšších harmonických frekvencích). Úlohy s okrajovými podmínkami se v praxi vyskytují v poměrně komplikovaných situacích (posuzování ne jednoho nosníku, ale celé konstrukce) a proto se zpravidla řeší přibližně a převádí se na řešení soustav lineárních rovnic.
Z přednášek o derivaci máme aproximace derivací \[ \frac{\mathrm d f}{\mathrm dx}=f'(x)\approx \frac{f(x+h)-f(x-h)}{2h} \] a \[ \frac{\mathrm d^2f}{\mathrm dx^2}=f''(x)\approx \frac{f(x-h)-2f(x)+f(x+h)}{h^2}. \] Využijeme tuto informaci k ukázce použití na příkladu nosníku s kombinovaným namá ním.

Příhradový nosník. Vzpěry jsou namáhány v ose. Teorii vybudoval v 18. století L. Euler, ale začala se dále rozvíjet a využívat až po sérii pádů příhradových železničních mostů v 19. století. Zdroj: www.ceskestavby.cz.
Příklad (podle Autar Kaw et al.: Finite Difference Method for Ordinary Differential Equations.) Deformace \(y\) nosníku délky \(L\) podepřeného na koncích, vystaveného vertikálnímu zatížení \(q\) a axiálnímu namáhání \(T\) je dána rovnicí \[\frac{d^2 y}{dx^2}-\frac {T}{EI} y=\frac{qx(L-x)}{2EI},\] kde \(E\) je materiálová charakteristika a \(I\) je veličina související s průřezem nosníku (kvadratický moment průřezu, souvisí s velikostí i s tvarem). Okrajové podmínky jsou \(y(0)=0\) a \(y(L)=0\). Po dosazení za druhou derivaci dostáváme \[\frac{y(x-h)-2y(x)+y(x+h)}{h^2}-\frac {T}{EI} y(x)=\frac{qx(L-x)}{2EI}.\] Pokud délku nosníku \(L\) rozdělíme na \(n\) částí délky \(h\) a pokud označíme \(x_i=ni\), \(y_i=y(x_i)\), rovnice se redukuje na rovnici \[\frac{y_{i-1}-2y_i+y_{i+1}}{h^2}-\frac {T}{EI} y_i=\frac{qx_i(L-x_i)}{2EI}.\] To je pro \(i\) od \(i=1\) po \(i=n-1\) celkem \(n-1\) lineárních rovnic. K tomu přidáváme rovnice na koncích podepřeného nosníku, kdy platí \(y_0=0\) a \(y_n=0\). Celkem tedy máme soustavu \(n+1\) lineárních rovnic o \(n+1\) neznámých. Soustava je řešitelná. Protože pro jemné dělení je rovnic obrovské množství, není vhodné se problém snažit zdolat metodami řešení rovnic známými ze střední školy. Problematika spadá do oboru nazývaného lineární algebra, kterému se začneme věnovat na příští přednášce.
Pro analogickou úlohu se vzpěrnou tlakovou pevností dřeva viz též A. Požgaj, Štruktúra a vlastnosti dreva str. 359.

A jaká je hlavní message? Zdroj: pixabay.com