Koncept (různé pojetí rychlosti)

Rychlost chápeme v různých kontextech. Podle kontextu se mění i jednotky, ve kterých rychlost určujeme. Zdroj: pixabay.com

• Jak rychle (v kilometrech za hodinu) se pohybuje atlet, kůň nebo baseballový balon?
• Jak rychle (v metrech za rok) roste strom do výšky?
• Jak rychle (v kubických metrech za rok) roste strom (tj. jak rychle přibývá na objemu)?
• Jak rychle (ve stupních Celsia za hodinu) klesá teplota uvnitř stavby?
• Jak rychle (ve stupních Celsia na centimetr) se mění teplota ve vnější zdi oddělující vytopený dům a venkovní prostředí?
• Jak rychle (v newtonech na metr) klesá gravitační síla při vzdalování se od Země?
• Jak rychle (v Kč na litr) rostou náklady výrobce pivovaru při zvyšování produkce?
• Jak rychle (v metrech krychlových na metr) klesá hustota vzduchu s výškou nad zemí?
• Jak rychle (v litrech na kilometr za hodinu) roste spotřeba auta při vyšší průměrné cestovní rychlosti?

Koncept (průměrná rychlost a okamžitá)

Určování rychlosti na stále kratším intervalu je jako bychom se dívali na funkci stále lepším mikroskopem. Matematika se umí podívat dokonce "mikroskopem s nekonečně velkým rozlišením". Zdroj: pixabay.com

Průměrnou rychlost určujeme tak, že změnu sledované veličiny přepočteme na jednotku času (u závislosti na čase), délky (u závislosti na poloze) nebo obecně na jednotku veličiny, na které sledovaná veličina závisí.

Průměrná rychlost s jakou se mění funkce \(f\) na intervalu \([x,x+h]\) je dána vztahem \[\frac{f(x+h)-f(x)}h.\]

Průměrná rychlost pracuje jenom s informací v koncových bodech intervalu a proto bohužel neobsahuje informaci, co přesně se děje uvnitř intervalu, přes který průměrujeme. Počítáme-li ale průměr přes stále kratší interval, nevýhoda průměrné rychlosti mizí. Cílem je počítat průměr přes interval prakticky nerozlišitelný od nuly. To by dalo okamžitou rychlost. Numerický experiment ukazuje, že u některých funkcí toto funguje pěkně, u některých bohužel ne.

Pokud průměrujeme za stále kratší čas, čitatel i jmenovatel se blíží k nule a jsou potíže s interpretací zlomku. Nulou totiž není možné dělit. Musíme vytvořit koncept, který umožní sledovat, co se děje s funkčními hodnotami funkce, pokud se vstupními daty jdeme "na krev" ke kraji definičního oboru.

K vyřešení problému použijeme pojem limita. Budeme se (zatím) soustředit na tzv. vlastní limitu ve vlastním bodě.

Limita

Buď \(f\colon \mathbb R\to\mathbb R\) funkce jedné proměnné

Definice (okolí).

Okolím bodu \(x_0\) rozumíme libovolný otevřený interval obsahující bod \(x_0\).

Definice (limita).

Řekneme, že funkce \(f\) má v bodě \(x_0\) limitu rovnu číslu \(L\) právě tehdy, když pro libovolnou předem zadanou toleranci (i extrémně malou) existuje okolí bodu \(x_0\) takové, že všechny body z okolí bodu \(x_0\) různé od \(x_0\) mají funkční hodnotu v rámci uvažované tolerance stejnou jako \(L\).

Pozorování. Většina funkcí má v bodech, kde jsou definované, limitu rovnu funkční hodnotě. Přesněji tuto myšlenku vystihuje koncept spojitosti.

Spojitost

Definice (spojitost).

Řekneme, že funkce \(f\) je spojitá v bodě \(x_0\) jestliže je v tomto bodě definovaná a má limitu rovnu funkční hodnotě. Řekneme, že funkce \(f\) je spojitá na otevřeném intervalu, je-li spojitá v každém jeho bodě.

Definice (elementární funkce).

Všechny mnohočleny, goniometrické, cyklometrické, exponenciální a logaritmické funkce a obecná mocnina se nazývají základní elementární funkce Všechny funkce, které ze základních elementárních funkcí získáme konečným počtem operací sčítání, odečítání, násobení, dělení a skládání těchto funkcí navzájem se nazývají elementární funkce.

Věta (spojitost elementárních funkcí).

Všechny elementární funkce jsou spojité v každém vnitřním bodě svého definičního oboru.

Podobně jako spojitost funkce jedné proměnné je definována spojitost funkcí více proměnných. Zůstane dokonce v platnosti předchozí věta. V naprosté většině základních praktických aplikací vystačíme s popisem pomocí elementárních funkcí a proto jsou funkce, se kterými pracujeme, zpravidla automaticky spojité. Opatrnost je nutné pouze tam, kde se od elementárních funkcí odchýlíme, například při použití nekonečných řad.

Poznámka.

Body, v jejichž okolí je funkce ohraničená, ale je zde porušena spojitost, jsou například následující.

skok

Na jeho odhalení stačí zvolit toleranci v definici limity menší, než je výška skoku. Například \(f(x)=\frac{|x|+x}{2x}\) je jednotkový skok v nule.

odstranitelná nespojitost

Tato nespojitost nás zajímá nejvíce. Je to nespojitost, která zmizí pokud vhodně dodefinujeme funkční hodnotu v bodě nespojitosti. Například funkce \[f(x)= \begin{cases} \frac {\sin x}{x}& x\neq 0\\ 1& x=0 \end{cases} \] je spojitá funkce. Vznikla doplněním jedné funkční hodnoty do definice funkce \(\frac{\sin x}x\), která má odstranitelnou nespojitost v bodě \(x=0\).

Grafy.

Derivace

Teď jsme připraveni (alespoň teoreticky) počítat průměrnou rychlost na intervalu, jehož délka je nerozlišitelná od nuly.

Buď \(y=f(x)\) funkce definovaná na nějakém otevřeném intervalu.

Definice (derivace).

Derivací funkce \(f\) v bodě \(x\) rozumíme limitu \[\frac{\mathrm df}{\mathrm dx}:=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h},\] pokud tato limita existuje a je konečná.

Derivaci funkce \(f\) v bodě \(x_0\) označujeme \(f'(x_0)\) nebo \(\frac{\mathrm df(x_0)}{\mathrm dx}\). Derivaci v libovolném bodě potom \(f'\), \(f'(x)\) nebo \(\frac{\mathrm df}{\mathrm dx}\). Zápis \(\frac{\mathrm df}{\mathrm dx}\) je Leibnizova notace, zápis \(f'\) je Lagrangeova notace.

Poznámka.

Rozšifrování definice derivace:

• Výraz z čitatele, tj. \(f(x+h)-f(x)\), je změna veličiny \(f\) na intervalu \([x,x+h]\). Často označujeme též \(\Delta f\).
• Podíl, tj. \(\frac{f(x+h)-f(x)}h\) je změna veličiny \(f\) na intervalu \([x,x+h]\) přepočítaná na jednotku veličiny \(x\), tj. v jistém smyslu průměrná rychlost na tomto intervalu. Často označujeme též \(\frac{\Delta f}{\Delta x}\).
• Limita v definici derivace stahuje délku intervalu, na kterém počítáme průměrnou rychlost, k nule. Tím se z průměrné rychlosti stane okamžitá rychlost.

Jednotka derivace je stejná, jako jednotka podílu \(\frac {f(x)}x\).

Derivace \(f'(x)\) udává, jak se mění veličina \(f\) při změnách veličiny \(x\). Interpretace derivace v nematematických disciplínách je okamžitá rychlost s jakou veličina \(f\) reaguje na změny veličiny \(x\).

Věta (existence derivace implikuje spojitost).

Má-li funkce \(f\) derivaci na intervalu \(I\), je na tomto intervalu spojitá.

Věta (znaménko derivace implikuje monotonii).

• Má-li funkce \(f\) kladnou derivaci na intervalu \(I\), je na tomto intervalu rostoucí.
• Má-li funkce \(f\) zápornou derivaci na intervalu \(I\), je na tomto intervalu klesající.

Aplikace derivací 1: Jak rychle? (změna v čase)

Rychlost ochlazování není konstantní, ale závisí na rozdílu teplot, který se během ochlazování stírá. Proces se v čase zpomaluje. Zdroj: Iva Balk, pixabay.com

Derivace v bodě, pokud ji nahlížíme z hlediska časové změny veličiny, která nás zajímá, je okamžitá rychlost s jakou se mění tato veličina.

Zákon ochlazování

Horké těleso o teplotě \(T\) je v chladnější místnosti o teplotě \(T_0\). Z fyziky je známo (Newtonův zákon tepelné výměny), že rychlost s jakou klesá teplota tělesa je úměrná teplotnímu rozdílu. Tento rozdíl je \(T-T_0\) (od většího odečítáme menší).

• Veličina \(T\) je teplota tělesa měřená například ve stupních Celsia.
• Veličina \(t\) je čas měřený například v hodinách.
• Derivace \(\frac{\mathrm dT}{\mathrm dt}\) ve stupních Celsia za hodinu je rychlost, s jakou roste teplota tělesa.
• Matematickým vyjádřením toho, že rychlost s jakou roste teplota a teplotní rozdíl \(T-T_0\) jsou úměrné je rovnice \[\frac{\mathrm dT}{\mathrm dt}=-k(T-T_0),\] kde \(k\) je konstanta úměrnosti a záporné znaménko vyjadřuje, že teplota klesá. Neznámou v této rovnici je funkce a v rovnici figuruje derivace této funkce. Takové rovnice se naučíme řešit později.

Poznámka (smysl předchozího příkladu).

Předchozí příklad je často v různých obměnách používán na modelování ochlazování kávy, což je proces, který většina lidí důvěrně zná. Nemáme pochopitelně ambice se domnívat, že bychom dokázali z této rovnice odvodit nějaké zásadní výsledky aplikovatelné při pití ranní kávy nebo při konzumaci horké polévky. Učíme se na malých věcech, abychom později mohli dělat věci velké. Na známých věcech se učíme aparát, který bude naším jediným nástrojem tam, kde intuice začne selhávat. Z tohoto příkladu je nutné si odnést, že derivace, jako rychlost změny, hraje roli při kvantitativním popisu dějů a při studia procesů, kdy se mění veličiny. Ať už doopravdy (studium pohybu nebo dějů, probíhajících v čase) nebo virtuálně (problémy spojené s mechanikou, včetně statiky, stability a deformací, často pracují s virtuálními změnami, tj. se změnami, které jsou sice z hlediska úlohy přípustné, ale příroda je z nějakého důvodu nerealizuje). Tedy naprostá většina dějů a jevů, které studujeme a chceme jim rozumět. Jakmile se v popisu fyzikálního zákona objeví slovo rychlost, někdy nahrazené souslovím časová změna, znamená to, že kvantitativní popis se děje pomocí derivací.

Při datování pomocí radioaktivního uhlíku využíváme toho, že rychlost procesu souvisí s tím, jak dlouho proces probíhá. Podobně jako u ochlazování. Zdroj: http://geologylearn.blogspot.com/.

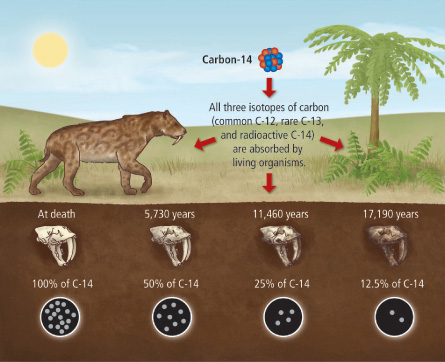
Uhlík 14C a datování organických nálezů

V roce 1940 byl objeven uhlík \(^{14}C\). Jedná se o radioaktivní prvek s mnoha skvělými vlastnostmi. Jednou z nich je vhodná rychlost rozpadu, která jej činí vhodným pro datování archeologických nálezů pozůstatků živých organismů

• Rychlost, s jakou se mění množství (a tedy i koncentrace \(y\) v daném vzorku) nerozpadnutého radioaktivního materiálu je úměrná jeho množství (a tedy i koncentraci). Tato skutečnost je přirozeným důsledkem toho, že pro daný nestabilní izotop mají všechny atomy stejnou pravděpodobnost, že u nich dojde k rozpadu a tato pravděpodobnost se s časem nemění. Kvantitativně je proces rozpadu popsán rovnicí \[\frac{\mathrm dy}{\mathrm dt}=-\lambda y,\] kde \(\lambda\) je konstanta úměrnosti.
• Uhlík je na datování vhodný, protože jej během života absorbují živé organismy a protože poločas rozpadu jej činí vhodným pro datování většiny archeologicky zajímavých nálezů. (Pro datování vzorků stařích než 50 tisíc let je nutné použít jiný prvek, protože v tomto případě již uhlíku \(^{14}C\) ve vzorku zůstane málo.)

Aplikace derivací 2: Jak strmě? (změna v prostoru)

Derivace v bodě, pokud ji nahlížíme z hlediska prostorové změny veličiny, která nás zajímá, je míra, jak nerovnomerně je veličina rozložena v prostoru. Často se tato veličina nazývá gradient, zejména pokud nepracujeme v jednorozměrném případě, ale pokud popisujeme děj probíhající v rovině nebo v prostoru.

Vedení tepla (dřevařství, nábytek, dřevostavby)

Nerovnoměrnost rozložení teploty v tělese vede k vyrovnávání teplot přenosem tepla. Uvažujme teplotu \(T\) tyče jako funkci polohy \(x\) na tyči. Ke kvantitativnímu vyjádření vedení tepla je nutné vědět, jaký rozdíl teplot připadá na jednotku délky. V homogenním případě vydělíme teplotní rozdíl vzdáleností. V obecném případě rychlost s jakou se mění teplota podél tyče (gradient teploty) vyjadřujeme pomocí derivace \[\frac{\mathrm dT}{\mathrm dx}.\] Využívá se v posuzování izolačních vlastností a při sušení dřeva.

Řez korytem. Voda zaplňuje koryto odspodu, tj. změna v množství vody v korytě se projeví nahoře, kde je šířka koryta \(B\). Zdroj: Wikipedia.

Derivace hraje roli při odvození podmínky pro vznik hydraulického skoku. Zdroj: Jonathan Ball, https://www.flickr.com/photos/jball359

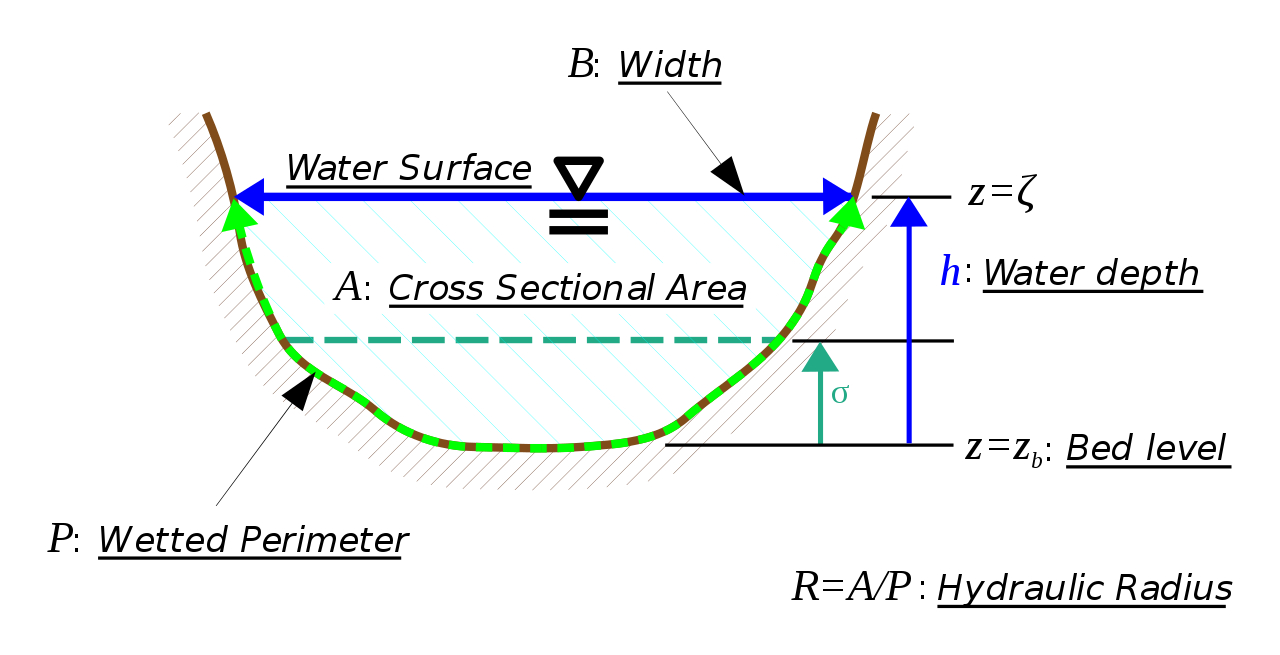
Koryto řeky (krajinářství)

Uvažujme příčný řez korytem řeky, jak je na obrázku. Z tohoto obrázku je zřejmé, že při zvyšování obsahu průřezu roste hladina. Pokud by stěny byly svislé (tj. \(B\) nezávislé na \(h\)), byla by změna průřezu \(\Delta A\) (například v milimetrech čtverečních) vyvolaná změnou výšky \(\Delta h\) (například v milimetrech) rovna šířce řeky \(B\) v milimetrech, protože koryto by bylo obdélníkové a podíl obsahu obdélníka a jeho výšky je šířka. V případě nekonstantního \(B\) dostáváme místo podílu derivaci, tj. \[\frac{\mathrm d A}{\mathrm dh}=B.\] Derivace průřezu koryta podle výšky koryta hraje důležitou roli například při přechodu říčního proudění v bystřinné. Tato veličina vyjadřuje, jak rychle se mění obsah průřezu s rostoucí hladinou. V praxi je možné ji spočítat pro speciální tvary koryta, proto jsou vzorce pro vodní skok související s tímto přechodem k dispozici jenom ve speciálních případech, jako například koryto obdélníkového tvaru.

Výpočet derivace

• Nikdy (nebo alespoň skoro nikdy) nederivujeme pomocí definice, ale používáme vzorce pro derivace základních elementárních funkcí a pro derivace matematických operací s funkcemi.
• Viz cvičení v prvním týdnu.

Aplikace derivací 3: Jak citlivě? (reakce na změnu)

Derivace v bodě, pokud ji nahlížíme z hlediska citlivosti reakce funkce na změnu vstupních dat, udává, jaký vliv má jednotková změna ve vstupních datech na zmenu funkční hodnoty funkce. Pokud změna ve vstupních datech není jednotková ale násobek jednotkové změny, je i odezva násobná.

Poznámka.

Buď \(f:\mathbb R\to\mathbb R\) funkce taková, že má derivaci. Pokud se veličina \(x\) změní z hodnoty \(x_0\) o hodnotu \(\Delta x\) (tj. nová hodnota je \(x_0+\Delta x\)), potom se \(f\) mění přibližně o \(f'(x_0)\Delta x\), tj. \[\Delta f\approx f'(x_0)\Delta x\] neboli \[\Delta f\approx \frac{\mathrm df(x_0)}{\mathrm dx}\Delta x.\] Tato aproximace je použitelná pro malé hodnoty \(\Delta x\).

Co se rozumí malou hodnotou \(\Delta x\) závisí na více faktorech, například i na tom, jak se funkce "vzpírá" tomu, být aproximována výrazem úměrným \(\Delta x\). Přesněji tuto podmínku zformulujeme po probrání Taylorova polynomu, kdy se použije o něco obecnější postup.

Příklad. Nosník výšky \(h\), šířky \(a\) a délky \(L\) je uprostřed zatížený silou \(F\). Průhyb \(s\) uprostřed nosníku je dán vztahem \[s=\frac {F L^3}{4Ebh^3},\tag{♣}\] kde \(E\) je materiálová konstanta. Pro \(h=20\,\mathrm{cm}\) je průhyb \(s=10\,\mathrm{cm}\). Zjistěte, jak se průhyb mění při změnách výšky nosníku. Odhadněte, jak se průhyb změní, pokud se \(h\) sníží na \(18\,\mathrm{cm}\)?

Řešení. Relevantními veličinami jsou \(s\) a \(h\) a vzorec je tedy možno shrnout do tvaru \[s=\frac k{h^3},\] kde \(k\) je konstanta charakterizující danou situaci. Pro zadané hodnoty výšky a průhybu vychází konstanta \[k=s h^3=10\times 20^3=80\,000.\] Vzorec (♣) tedy redukujeme na \[s={80\,000}{h^{-3}}.\] Derivováním obdržíme \[\frac{\mathrm ds}{\mathrm dh}=80\,000\times(-3) h^{-4}=-\frac{3\times 80\,000}{h^4}.\] Změna výšky nosníku je \[\Delta h=18-20=-2\,\mathrm{cm}\] a tomu odpovídá změna průhybu \[\Delta s=-\frac{3\times 80\,000}{(20)^4}(-2)=3\,\mathrm{cm}.\] Průhyb se tedy zvětší o \(3\,\mathrm{cm}\).

Poznámka (smysl předchozího příkladu).

Proč nepočítáme přesně? Stačila by selská logika a změna funkce \(s=\frac k{h^3}\) by byla \[\Delta s=\frac k{(h+\Delta h)^3}-\frac k{h^3}.\tag{♠}\] Odpověď je překvapivá: pomocí derivací je vyjádření změny v naprosté většině případů jednodušší. V tomto našem případě máme \[\Delta s\approx -\frac{3k}{h^4}\Delta h,\] což je na další práci mnohem příjemnější výraz, než rozdíl dvou zlomků (♠). Skutečnost, že platí pouze pro malé \(\Delta h\) nás nijak neomezuje. Většinou se tento aparát používá tam, kde se chyba limitním přechodem "stáhne na nulu". Navíc, ukazujeme koncept. Důležité je si z příkladu odnést, že derivace umožní analyzovat, jak vypočítané veličiny reagují na změny ve vstupních datech. Výsledkem může být například maximální teoretická přesnost se kterou je možné vypočítat výslednou veličinu při vstupních datech zatížených chybou nebo nějakým způsobem nejistých (zákon šíření chyb).

Koncept (parciální derivace)

Tepelně modifikované dřevo (napravo). Jak rychle uvnitř roste teplota? Jak dlouho musíme tepelně opracovávat, aby se teplota dostatečně zvýšila v celém objemu? Zdroj: Wikipedia

Derivace je vhodná ke studiu fyzikálních procesů na makroskopické úrovni těles. Pro vyjadřování procesů jako jsou rychlost změny teploty tělesa nebo množství tekutiny v daném objemu jsou vhodné (obyčejné) derivace.

Někdy však požadujeme detailnější informace o celém procesu, abychom měli přesnější popis a dokázali odhalit vliv všech relevantních parametrů. U tepelné výměny bychom například sledovali, jak se teplo předává z jednoho místa tělesa do druhého místa a jak prostupuje tělesem. Takový pohled je nutný například při studiu procesu, který není stacionární v čase. Při tomto pohledu již musíme znát teplotu nejen jako funkci času, ale i jako funkci prostorových souřadnic. Musíme tedy pracovat modelem, kdy teplota, nebo obecně nějaká stavová veličina, závisí na více faktorech. Musíme tedy pracovat s funkcemi více proměnných a studovat, jak se mění vzhledem k jednotlivým proměnným. To je přesně úkol pro diferenciální počet funkcí více proměnných a parciální derivace.

Výsledkem tohoto přístupu je formulace zákonů v diferenciálním tvaru. Tento tvar říká, co se děje v konkrétním místě a dává lepší náhled na fyzikální podstatu. Proto tomuto přístupu často dáváme přednost před makroskopickým pohledem na těleso jako na jeden celek.

Parciální derivace

Definice (parciální derivace).

Buď \(f\colon \mathbb R^2\to\mathbb R\) funkce dvou proměnných, \(x\) a \(y\), tj. \(f(x,y)\). Výraz \[\frac{\partial f}{\partial x}:=\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}h\] se nazývá parciální derivace funkce \(f\) podle \(x\). Podobně, \[\frac{\partial f}{\partial y}:=\lim_{h\to 0}\frac{f(x,y+h)-f(x,y)}h\] je parciální derivace funkce \(f\) podle \(y\).

Podobně můžeme definovat parciální derivaci pro funkce libovolného konečného počtu proměnných. V těchto parciálních derivacích vlastně sledujeme, jak reaguje veličina \(f\) na změny jenom v jedné proměnné. Proměnná, přes kterou se nederivuje, má vlastně roli parametru, nijak se nemění.

Rovnice vedení tepla v 1D

Studujme vedení tepla v jednorozměrné tyči. Teplota je funkcí dvou proměnných, polohy a času.

Poznámka.

Potřebujeme fyzikální zákony řídící vedení tepla. Bez nich matematika model vedení tepla nemá jak naformulovat. Tyto zákony je potřeba matematice dodat "z venku", z aplikované vědy. Tou je v tomto případě fyzika, jindy může být biologie nebo geologie. Jakmile jsou potřebné zákony a případně materiálové vztahy k dispozici, stavé se problém čistě matematickým a fyzika přijde ke slovu při závěrečné interpretaci. Použijeme následující fyzikální fakta.

• Rozdílem teplot vzniká tok tepla. Velikost toku tepla je úměrná teplotnímu rozdílu.
• Teplota se zvyšuje dodáním tepla. Pro zvýšení teploty tělesa o hmotnosti \(m\) o hodnotu \(\Delta T\) je nutné dodat \[Q=mc\Delta T,\tag{**}\] kde \(c\) je měrná tepelná kapacita.
• Budeme vztahy formulovat pro změny za časovou jednotku a pro jednotkový objem (tedy místo hmotnosti \(m\), změny teploty \(\Delta T\) a tepla \(Q\) máme hustotu \(\rho\), rychlost změny teploty \(\frac{\partial T}{\partial t}\) a rychlost s jakou dodáváme teplo do daného místa vztažená na jednotkový objemu).

V dalším už nastupuje matematický popis a ve vhodných chvílích vždy použijeme výše uvedené fyzikální zákony. Mluvíme o teple, ale jako mechanický model si můžeme představit proudění tekutiny (pro jednoduchou představu) nebo proudění vlhkosti (pro odvození rovnice difuze namísto rovnice vedení tepla).

• Potřebujeme vědět, jak moc se mění teplota podél tyče. Změny v prostorovém rozložení teploty zachycuje derivace \(\frac{\partial T}{\partial x}\) v jednotkách (například) stupeň Celsia na centimetr.
• Potřebujeme změnu teploty podél tyče převést na veličinu popisující proudění tepla. Tok tepla je úměrný veličině popisující změnu rozložení tepla v prostoru, \[q=-k\frac{\partial T}{\partial x}.\tag{***}\]
  • Znaménko mínus vyjadřuje skutečnost, že teplo teče z míst s vyšší teplotou do míst s menší teplotou a že tok uvažujeme kladný, pokud teče ve směru osy \(x\). Přesněji, pokud teplota roste směrem doprava, parciální derivace je kladná, ale teplo teče doleva, tedy tok musí být záporný.
  • Veličina \(k\) je konstanta úměrnosti umožňující překalibrování změny prostorového rozložení teploty na tok tepla jendotkovým průřezem (první odrážka).
• Potřebujeme zjistit, kolik tepla za jednotku času přiteče do nějakého bodu a v tomto bodě "zůstane". Množství, které zůstane, je rozdílem mezi množstvím, které přiteče, a množstvím, které odteče. Tedy potřebuji vědět, jak se mění tok tepla podél tyče. Rychlost s jakou roste rychlost toku podél tyče je \(\frac{\partial q}{\partial x}\). My pro kladný ohřev potřebujeme pokles toku tepla, tedy násobíme záporným znaménkem a dostáváme \(-\frac{\partial q}{\partial x}\).
• Víme, kolik tepla se v daném místě spotřebuje na zvýšení teploty a tuto hodnotu musíme převést na změnu teploty (třetí odrážka). Opět se jedná o jakési překalibrování, které ještě souvisí s dalšími fyzikálními vlastnostmi jako je měrná tepelná kapacita a hmotnost jednotkového množství látky objemu v daném místě. Teplo \(-\frac{\partial q}{\partial x}\) je teplo, které každou časovou jednotku "zůstává" v bodě \(x\). Toto teplo se "použije" na zvýšení teploty. Z rovnice (**) pro jednotku času a jednotku objemu \[-\frac {\partial q}{\partial x}=\rho c\frac{\partial T}{\partial t}.\]
• Po dosazení za \(q\) dostáváme \[-\frac{\partial}{\partial x}\left(-k\frac{\partial T}{\partial x}\right)=\rho c\frac{\partial T}{\partial t}.\]
• Derivace konstantního násobku je konstantní násobek derivace. Veličina \(k\) by konstantní být nemusela a proto ji z opatrnosti necháme na svém místě. Může v ní být nehomogenita nebo se může měnit s teplotou, tj. vztah (***) může být nelineární. Znaménko mínus reprezentuje násobení konstantou \(-1\). Toto vede na finální tvar \[\frac{\partial}{\partial x}\left(k\frac{\partial T}{\partial x}\right)=\rho c\frac{\partial T}{\partial t}.\]

Shrnutí. V odvození vidíme, že rovnice vedení tepla je vlastně bilance toku tepla. Rozdíl o kolik se v daném místě snižuje tok tepla udává, kolik tepla se v daném místě spotřebovalo. Tato spotřeba tepla se projeví zvýšením teploty v daném bodě.

Gradient

Rovnici vedení tepla ve 2D a 3D uvedeme později. Může nastat problém s tím, že teplo neteče stejným směrem jaký odpovídá gradientu teploty. Je to podobné, jako pohyb vzduchu nebo podzemní vody způsobený rozdílem tlaku: voda nebo vzduch míří do míst s nižším tlakem, ale přitom volí cestu menšího odporu. Problém vyřešíme nástrojem, který umožní změnit směr vektoru: matice a maticové násobení. Teď uvedeme jenom veličinu, která umožní kvantifikovat, jakým směrem působí síla uvádějící příslušnou stavovou veličinu do pohybu.

Definice (gradient).

Buď \(f(x,y)\) funkce dvou proměnných, která má parciální derivace. Gradientem funkce \(f\) rozumíme vektor \[\mathop{\text{grad}}f:=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right).\]

Poznámka. Formálně též často píšeme \[\left(\frac{\partial}{\partial x},\frac\partial{\partial y}\right)f\] nebo \[\nabla f,\] kde \(\nabla=\left(\frac{\partial}{\partial x},\frac\partial{\partial y}\right)\) je operátor, se kterým pracujeme jako s vektorem. Nazývá se nabla nebo Hamiltonův operátor. Výsledkem gradientu je vektor ve směru maximálního růstu veličiny \(f\). V praxi nás většinou zajímá směr maximálního poklesu, tj. \(-\nabla f\).

Shrnutí, hlavní myšlenky

A jaká je hlavní message? Zdroj: pixabay.com

• Aplikované vědy (fyzika, biologie, nauka o materiálu, hydrologie) přirozeně formulují své zákony a poznatky mimo jiné i kvantitavině a pomocí pojmů vyjadřujících rychlosti změn. Doteď jsme aparátem střední školy uměli počítat jenom průměrně rychlosti za daný časový interval, s derivací dostáváme do ruky nástroj pro práci s okamžitými rychlostmi.
• Jakmile ve slovním popisu procesu slyšíme slovo rychlost, znamená to, že při matematickém modelování hraje pravděpodobně důležitou roli derivace. Okamžitá rychlost je derivace. Jenom v krásných případech probíhajících konstantní rychlostí můžeme tuto rychlost počítat pomocí podílu, jak to známe u rychlosti pohybu.
• Naučili jsme se nebo se naučíme pomocí vzorců derivovat bežné funkce.
• Derivace umožní předpovědět, co se stane s veličinou, která závisí na jiné veličině a tato jiná veličina se mění známou rychlostí. Ze vztahu, který dává do souvislosti hodnoty dvou veličin, můžeme určit pomocí derivací vztah, dávající do souvislosti rychlosti změn těchto veličin.
• V případě nutnosti umíme rozšířit derivace i do světa funkcí více proměnných. Děláme to tak, že sledujeme rychlost změny způsobenou vždy změnou jenom jedné veličiny. Proto příslušné derivace nazýváme parciální. (Parciální znamená v tomto smyslu částečný.)