
Pro provedení konkrétního výpočtu jsou nutná detailní znalosti výpočetního nástroje. Pro zvládnutí šířky aplikací je naopak nutný mít dostatečný nadhled zastírající jednotlivé detaily. Zdroj: pixabay.com

Pro provedení konkrétního výpočtu jsou nutná detailní znalosti výpočetního nástroje. Pro zvládnutí šířky aplikací je naopak nutný mít dostatečný nadhled zastírající jednotlivé detaily. Zdroj: pixabay.com
S využitím aparátu derivací jsme v minulé přednášce poznali a naučili se ve cvičení řešit úlohy tří základních různých typů:
Newton a Einstein. Každý dodá vzorec pro kinetickou energii, vzorce jsou jiné a přesto oba správně. Zdroj: https://www.science.org.au/curious/space-time/gravity

Pokud má funkce derivaci, dokážeme předvídat její chování. Nevidíme však daleko dopředu nebo dozadu, informace platí jenom v lokálně. Naše předpověď je prostě poněkud nejistá. Zdroj: pixabay.com
V minulé přednášce jsme si ukázali, že pokud má funkce \(f\) v bodě \(x_0\) derivaci \(f'(x_0)\) a pokud se veličina \(x\) změní z hodnoty \(x_0\) o hodnotu \(\Delta x\) (tj. nová hodnota je \(x_0+\Delta x\)), potom se \(f\) mění přibližně o \(f'(x_0)\Delta x\).
Nyní tento koncept rozšíříme. Nejprve se budeme snažit aproximovat celou funkci (a ne jenom její změnu) a poté budeme aproximaci zpřesňovat.
Věta.
Buď \(f:\mathbb R\to\mathbb R\) funkce, která má derivaci. V okolí bodu \(x_0\) platí přibližný vzorec \[f(x)\approx f(x_0)+ f'(x_0)(x-x_0)\] neboli \[f(x)\approx f(x_0)+ \frac{\mathrm df(x_0)}{\mathrm dx}(x-x_0).\]
Poznámka.
Výše uvedený vzorec není těžké rozšifrovat.
- Veličina \(f(x)\) je funkční hodnota v bodě \(x\), tu chceme odhadnout.
- Veličina \(f(x_0)\) je známá funkční hodnota v bodě \(x_0\), to je výchozí bod pro odhad.
- Veličina \(f'(x_0)\) je odhad změny veličiny \(f\) způsobený jednotkovou změnou vstupních dat (zvýšení hodnoty \(x_0\) o jednotku). Tento faktor ještě v dalším kroku musíme přizpůsobit tomu, že změna vstupních dat není jednotková, což uděláme s využitím přímé úměrnosti.
- Veličina \(f'(x_0)(x-x_0)\) je odhad změny veličiny \(f\) vyvolané změnou veličiny \(x\) z \(x_0\) o \(\Delta x=x-x_0\) tak, jak jsme jej používali v minulé přednášce.
Příklad (růst stromu). Strom má v roce 2019 výšku 3 metry a roste rychlostí 0.5 metru za rok. V roce \(x\) je jeho výška dána vzorcem \[h(x)=3+0.5(x-2019).\]
Příklad (aproximace důležitých funkcí v okolí nuly). Ve cvičení ukážeme platnost následujících přibližných vzorců, které platí pro \(x\) blízké k nule. \[\sin x\approx x, \quad \cos x\approx 1,\qquad (1+x)^n=1+nx.\] První dva vzorce využijeme později při popisu malých rotací v rovině. Mnoho důležitých aplikací těchto vzorců ve fyzice je na webu fyzikální olympiády v dokumentu Aproximace ve fyzikálních úlohách.

Vrcholek hory Chimborazo je místo nejvzdálenější od středu Země. Roli hraje nadmořská výška a zploštění Země. Gravitační zrychlení zde je nejmenší. Zdroj: pixabay.com
Příklad (gravitační potenciál v malých výškách nad zemí). Gravitační potenciál \(V\) ve vzdálenosti \(r\) od středu koule o hmotnosti \(M\) je dán vztahem \[V(r)=-G\frac Mr=-GMr^{-1},\] kde \(G\) je gravitační konstanta. Najdeme lineární aproximaci v bodě \(R\).
Dosazením obdržíme \[V(R)=-GMR^{-1}\] a derivováním \[\frac{\mathrm dV}{\mathrm dr}=GMr^{-2}, \quad \frac{\mathrm dV(R)}{\mathrm dr}=GMR^{-2}. \] Odsud poté získáme lineární aproximaci \[V(r)\approx -GMR^{-1}+GMR^{-2}(r-R)\] Pro Zemi jako kouli o poloměru \(R\) je \(r-R\) výška nad Zemí \(h\) a aproximaci je možno po přeznačení napsat ve tvaru \[V(r)\approx V_0 +gh.\] V tomto označení je \(V_0=-GMR^{-1}\) konstanta související s volbou nulové hladiny potenciálu a vzhledem k libovolnosti volby nulové hladiny je tato hodnota nepodstatná. Veličina \(g=GMR^{-2}\) je tíhové zrychlení vyjádřené pomocí gravitační konstanty \(G\) a parametrů Země. Veličina \(gh\) je potenciál v tíhovém poli Země. Tuto veličinu známe lépe ze vzorce pro potenciální energii tělesa o hmotnosti \(m\), který má tvar \[E=mgh.\]
Online výpočet tíhového zrychlení
Příklad (potenciální a kinetická energie). V předchozím příkladě je možné využít vztah \[(1\pm x)^n\approx 1\pm nx ,\quad \text{pro malé }x.\] Přepsáním gravitačního potenciálu \(V\) do tvaru obsahujícího výšku nad zemí \(h\) a využitím lineární aproximace získáme \[V = -G \frac{M}{R+h} =-G \frac{M}{R}\left (1+\frac hR\right)^{-1} \approx -G \frac MR\left(1+(-1)\frac hR\right) =-G \frac{M}{R} + G \frac{M}{R^2} h\] a po zavedení nových konstant \[ V\approx V_0+ g h,\] kde \(g=G \frac{M}{R^2}\).
Podobně aproximací přesných vztahů plynoucích z Einsteinovy teorie relativity získáme složku energie související s pohybem, tj. kinetickou energii \[E=\frac{m_0c^2}{\sqrt{1-\frac {v^2}{c^2}}} =m_0 c^2 \left(1-\frac {v^2}{c^2}\right)^{-1/2} \approx m_0c^2+\frac 12 m_0v^2 \] pro \(v\) mnohem menší než \(c\). Snadno rozšifrujeme, že s rychlostí souvisí jenom druhý sčítanec a že se jedná o klasický vzorec pro kinetickou energii \(\frac 12 mv^2\).
Ač se jedná "jenom" o lineární aproximaci, je vzorec \(E=\frac 12 mv^2\) dokonce mnohem použitelnější, protože výpočet kinetické energie pomocí univerzálně platného relativistického vzorce při malých rychlostech v praxi obvykle zhavaruje na zaokrouhlovacích chybách.
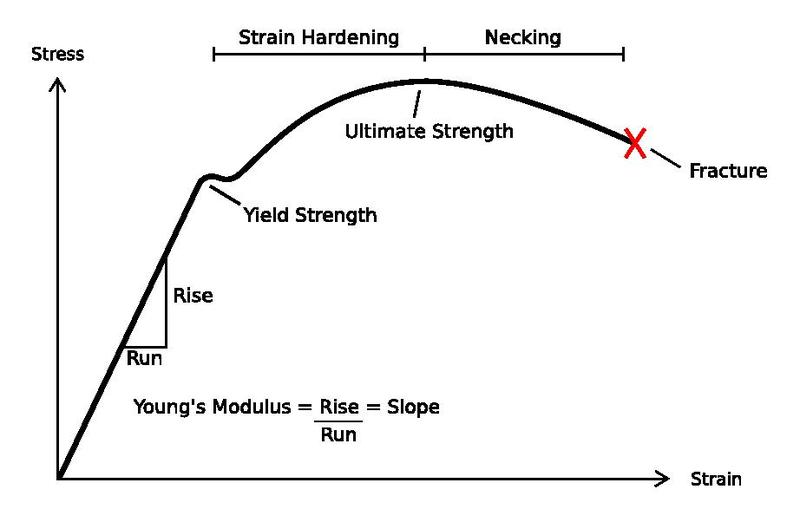
Podnět a materiálová odezva v případě mechanického namáhání oceli s malým obsahem uhlíku. Pěkně vidíme lineární závislost v okolí počátku a odklon od lineární závislosti pro velké namáhání. Zdroj: https://en.wikipedia.org, Breakeydown
V inženýrské praxi často potřebujeme modelovat odezvu materiálu reagujícího na vnější podnět. Může se jednat například o změnu délky při mechanickém namáhání, tok tepla materiálem při tepelném namáhání, tok tekutiny porézním materiálem (dřevo, půda) při difuzi nebo rozdílu tlaků a podobně.
Pokusíme se modelovat funkci dávající do souvislosti velikost podnětu a reakci materiálu.
Lineární aproximace funkce je vlastně aproximace tečnou. Protože pojem tečna ze střední školy chápeme jenom intuitivně, můžeme nyní pomocí derivace tečnu dokonce definovat. Z geometrického pohledu je tečna přímka bodem \([x_0,f(x_0)]\), která má směrnici \(f'(x_0)\). Proto se o derivaci často mluví jako o směrnici tečny.
Definice (tečna).
Nechť \(f\) je funkce, která má v bodě \(x_0\) derivaci \(f(x_0)\). Přímka \[y=f(x_0)+f'(x_0)(x-x_0)\] se nazývá tečna ke grafu funkce \(f\) v bodě \(x_0\).
Díky souvislosti derivace s tečnou je derivace jedinečným nástrojem při popisu vlastností křivek. Příslušná oblast se nazývá diferenciální geometrie a je to jakási oblast mezi geometrií a diferenciálním počtem.
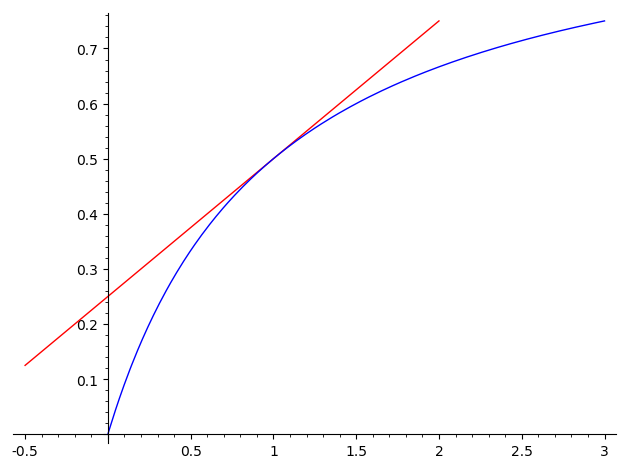
Pokud se rychlost růstu snižuje, je lineární aproximace nadhodnocená a funkční hodnoty jsou ve skutečnosti nižší.
Lineární aproximace vychází z předpokladu, že rychlost růstu (nebo poklesu) se příliš nemění. Někdy můžeme mít dodatečnou informaci o tom, jak se tato rychlost změní. Například pokud se bude rychlost zpomalovat, bude skutečná hodnota funkce menší než lineární aproximace.
Je otázka, zda a jak je možné informaci o tom, jak rychle roste rychlost, případně jak rychle roste rychlost růstu rychlosti, využít. To znamená že budeme studovat derivaci derivace, derivaci derivace derivace atd.
Aproximaci funkce \(\cos x\approx 1\) odvozenou výše, kdy aproximujeme vlastně konstantní funkcí, je možné také chápat jako selhání lineární aproximace. Následující slidy a pojem Taylorův polynom nám umožní najít prostředek pro aproximaci i v těchto případech.
Definice (druhá a další vyšší derivace).
- Druhou derivací rozumíme derivaci derivace. Označujeme \(f''(x)\) nebo \(\frac{\mathrm d^2 f}{\mathrm dx^2}\).
- Podobně \(k\)-tou derivací rozumíme derivaci \((k-1)\)-ní derivace. Označujeme \(f^{(k)}(x)\) nebo \(\frac{\mathrm d^k f}{\mathrm dx^k}\).
Platí tedy \[\frac {\mathrm d^2 f}{\mathrm dx^2}:=\frac {\mathrm d}{\mathrm dx} \left(\frac {\mathrm d f}{\mathrm dx}\right),\quad \frac {\mathrm d^kf}{\mathrm dx^k}:=\frac {\mathrm d}{\mathrm dx} \left(\frac {\mathrm d^{k-1}f}{\mathrm dx^{k-1}}\right) \] aneb \[f'':=(f')', \quad f'''=(f'')', \quad f^{(k)}={(f^{(k-1)})'}.\]
Označení derivací pomocí čárek se nazývá Lagrangeova notace, označení pomocí podílu diferenciálů Leibnizova notace. Ještě se někdy používá i Eulerova notace, používající \(\mathrm Df\), \(\mathrm D^2 f\) a \(\mathrm D^k f\) pro první, druhou a \(k\)-tou derivaci.
Příklad.
Podobně je možné pracovat s parciálními derivacemi parciálních derivací. Například \[\frac{\partial ^2 f}{\partial x^2}:=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial x}\right)\] \[\frac{\partial ^2 f}{\partial y^2}:=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial y}\right)\] nebo \[\frac{\partial ^2 f}{\partial x\partial y}:=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\right).\]
Definice (Taylorův polynom).
Taylorův polynom stupně \(n\) pro funkci \(f\) v bodě \(x_0\) je polynom \[T(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2!}f''(x_0)(x-x_0)^2+\cdots +\frac{1}{n!}f^{(n)}(x_0)(x-x_0)^n,\] tj. \[T(x)=f(x_0)+\frac {\mathrm df(x_0)}{\mathrm dx}(x-x_0)+\frac{1}{2!} \frac {\mathrm d^2f(x_0)}{\mathrm dx^2} (x-x_0)^2+\cdots +\frac{1}{n!}\frac {\mathrm d^nf(x_0)}{\mathrm dx^n}(x-x_0)^n.\]
Věta (Taylorova věta s Lagrangeovým tvarem zbytku).
Platí \[f(x)-T(x)=\frac{1}{(n+1)!}\frac {\mathrm d^{n+1}f(\xi)}{\mathrm dx^{n+1}}(x-x_0)^{n+1},\] kde \(\xi\in(x_0,x)\) je vhodné číslo. Pravá strana této rovnice je blízká k nule, pokud je \(n\) dostatečně velké, \(x\) dostatečně blízko k \(x_0\) a \((n+1)\)-ní derivace funkce \(f\) je relativně malá. V těchto případech je \[f(x)\approx T(x).\]
Příklad. \[ \begin{aligned} \ln \frac{1+x}{1-x}&\approx 2x+\frac 23 x^3+\frac 25 x^5+\frac 27 x^7 +\frac 29 x^9\\ \ln 2=\ln\frac {1+\frac 13}{1-\frac 13}&\approx 0.69314604 \end{aligned}\] Po tomto výpočtu je prvních pět cifer aproximace \(\ln 2\) správně. Tady vidíme i jeden zajímavý trik. Pokud bychom se snažili napsat Taylorův polynom funkce \(\ln (x+1)\), která vypadá příjemněji, chyba aproximace by byla mnohem větší.
Příklad. Výraz \[V(r)=\frac 1{r^{12}}-\frac 2{r^6}=r^{-12}-2r^{-6}\] je (až na konstanty, které pro pohodlí volíme pevně) Lennard-Jonesův potenciál často používaný pro interakci mezi atomy nebo molekulami. Napíšeme Taylorův polynom druhého stupně v bodě \(r=1\). K tomu potřebujeme znát funkční hodnotu a hodnotu prvních dvou derivací v tomto bodě. \[\begin{aligned} V(1)&=1-2=-1\\ \frac{\mathrm dV}{\mathrm dr}&=-12r^{-13}-2(-6)r^{-7}\Bigr|_{r=1}=-12+12=0\\ \frac{\mathrm d^2V}{\mathrm dr^2}&=12\cdot 13 r^{-14}-2\cdot6\cdot 7r^{-8}\Bigr|_{r=1}=12\cdot 13-12\cdot 7=72\\ V(r)&\approx -1+\frac 12 72 (r-1)^2 \end{aligned} \] Konstanta \(-1\) je nezajímavá, souvisí s nulovou hladinou potenciálu a nulovou hladinu potenciálu si můžeme volit libovolně.
Lineární člen chybí a kvadratický člen je analogický potenciální energii pružiny o tuhosti \(k\) ve tvaru \[U=\frac 12 kx^2.\] Molekuly či atomy popsané tímto potenciálem se chovají jako tělesa na pružině o tuhosti \(k=72\). Pro atom o hmotnosti \(m\) tedy například platí vzorec pro úhlovou frekvenci oscilací \(\omega = \sqrt{\frac km}\), odvozený původně pro těleso na pružině. Veličina \(r-1\) je výchylka z rovnovážného stavu. Analogicky se chovají pružné konstrukce. V klidu jsou ve stavu s minimální potenciální energií a při vychýlení z tohoto stavu o malou hodnotu začínají kmitat. Pokud aproximujeme potenciál pomocí Taylorova polynomu, z koeficientu u kvadratického člene můžeme určit frekvenci těchto oscilací.
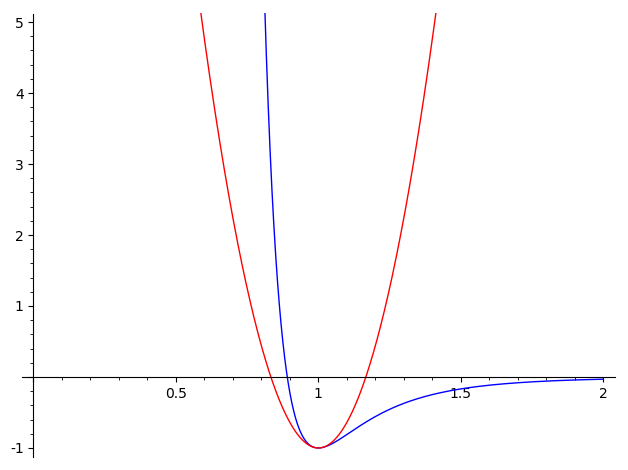
Znalost minima potenciální energie je často zásadní pro nalezení stabilní konfigurace systému. Od molekul po soustavy těles. Musíme mít univerzální postup, jak tato minima hledat.
V příkladě s aproximací potenciálu pomocí Taylorova polynomu se nám povedlo potenciál aproximovat pomocí kvadratické funkce v okolí vrcholu paraboly. To je častá úloha, protože systémy s potenciální energií se často nacházejí ve stavu blízkému minimu této energie. Otázka je, jak toto minimum najít. Budeme řešit poněkud obecnější úlohu, jak hledat nejenom minimální hodnotu, ale i maximální hodnotu. Zaměříme se na minima a maxima, která jsou lokální (platná pouze na určitém intervalu, třeba i krátkém).
Následující definice si všímají bodů které mají tu vlastnost, že v okolí není možné najít body buď s vyšší funkční hodnotou (potom se jedná o lokální maximum, nikde v okolí mi funkce neukáže více) nebo s nižší funkční hodnotou (analogicky, lokální minimum).
Definice (lokální extrémy).
Nechť \(f\colon \mathbb R\to\mathbb R\).
- Řekneme, že \(f\) má v bodě \(x_0\) lokální maximum, pokud platí \[f(x)\leq f(x_0)\] pro všechna \(x\) z nějakého okolí bodu \(x_0\).
- Řekneme, že \(f\) má v bodě \(x_0\) lokální minimum, pokud platí \[f(x)\geq f(x_0)\] pro všechna \(x\) z nějakého okolí bodu \(x_0\).
- Řekneme, že \(f\) má v bodě \(x_0\) lokální extrém, pokud v tomto bodě má buď lokální maximum nebo lokální minimum.
Přímo z definice lokálních extrémů a rostoucí a klesající funkce plyne, že funkce nemůže mít lokální extrém v bodě, kde je rostoucí nebo kde je klesající. Tuto skutečnost vyjadřuje pomocí derivací následující věta.
Věta (Fermatova o lokálním extrému).
Má-li funkce \(f\) v bodě \(x_0\) lokální extrém, potom je derivace funkce \(f\) v bodě \(x_0\) nulová, nebo neexistuje.
Předchozí věta eliminuje obrovské množství bodů z definičního oboru funkce. V prakticky využitelných případech nám po této eliminaci často zůstane jenom jediný bod, podobně jako v následující úloze.

Ukázka zpracování kulatiny na trám sekerou. Zdroj: https://www.bladeforums.com
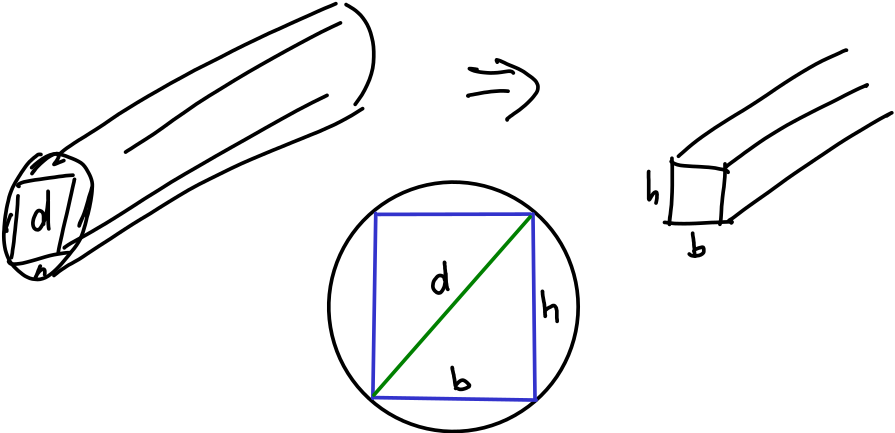
K problému vyřezání co nejtužšího nosníku. Budme předpokládat krásný kmen, dokonalý válec bez vad, které by nás limitovaly při plánování, jak má výsledný trám vypadat.
Příklad. Z kulatiny o průměru \(d\) chceme získat nosník obdélníkového průřezu, který se při zatížení co nejméně prohýbá. Z fyzikálních úvah víme, že musí být maximální součin \(bh^3\), kde \(b\) je šířka a \(h\) výška nosníku.
Trik 1: Budeme měřit jednotky v násobcích průměru. Proto je \(d=1\). Můžeme tedy bez újmy na obecnosti předpokládat, že kulatina má jednotkový průměr.
Z Pythagorovy věty (nakreslete si průřez, tj. obdélník vepsaný do kružnice) plyne \(b=\sqrt{1-h^2}\) a snažíme se tedy řešit úlohu \[bh^3=h^3 \sqrt{1-h^2}\to \mathrm{MAX},\] která má fyzikální smysl na intervalu \((0,\infty)\).
Trik 2: Protože uvažujeme jenom kladné délky, je funkce kladná a bude maximální tam, kde bude maximální její druhé mocnina. Je tedy možné studovat ekvivalentní úlohu \[(bh^3)^2=h^6(1-h^2)=h^6-h^8\to \mathrm{MAX}\] na intervalu \((0,\infty)\). Výhoda je zřejmá: místo součinu dvou funkcí, z nichž jedna je navíc složená, studujeme dvoučlenný polynom. Pro funkci \[f(h)=h^6-h^8\] dostáváme \[ \frac{\mathrm df}{\mathrm dh}=6h^5-8h^7=2h^5(3-4h^2).\] Tato derivace je nulová pro \[h^2=\frac 34\] tj. \[h=\frac{\sqrt 3}2.\] Pro tuto výšku bude mít nosník maximální hodnotu tuhosti. Šířka nosníku bude \[b=\sqrt{1-h^2}=\sqrt{1-\frac 34}=\sqrt{\frac 14}=\frac 12.\] Poměr výšky a šířky u nosníku maximální tuhosti tedy bude \(\sqrt{3}:1\) a šířka bude rovna polovině průměru.
Poznámka.
Někdy se při studiu lokálních extrémů hodí dva následující triky.
- Vhodnou volbou jednotek dokážeme eliminovat některé parametry. Přesněji, vhodnou volnou jednotek dokážeme některým parametrům dát konkrétní numerickou hodnotu. Vyšetřovaná funkce je potom často jednodušší.
- Je-li \(g\) rostoucí, potom z definice rostoucí funkce plynou ekvivalence \[ \begin{gathered} f(x)\leq f(x_0) \iff g(f(x))\leq g(f(x_0)),\\ f(x)\geq f(x_0) \iff g(f(x))\geq g(f(x_0)) \end{gathered} \] a proto funkce \(f(x)\) a \(g(f(x))\) mají lokální extrémy ve stejných bodech. Toho je možné využít, pokud vidíme, že při vhodné volbě funkce \(g\) by byla funkce \(g(f(x))\) vhodnější pro hledání lokálních extrémů. Podobně je možné uvažovat i pro klesající funkce \(g\), ale protože klesající funkce obrací směr nerovností, mění se lokální maximum na lokální minimum a naopak.
Pokud řešíme úlohu s praktickým zadáním, je z povahy úlohy často zřejmé, že lokální extrém požadovaného typu existuje a často to bývá jediný bod, kde je derivace nulová. Pokud takových bodů máme více, nebo pokud je situace méně zřejmá, můžeme existenci lokálního extrému posoudit pomocí následující věty.
Věta (postačující podmínka pro lokální extrémy).
Je-li \(f\) spojitá v bodě \(x_0\) a mění-li se v bodě \(x_0\) funkce \(f\) z rostoucí na klesající, má funkce \(f\) v bodě \(x_0\) lokální maximum. Analogicky, lokální minimum nastává při změně z klesající na rostoucí.
Podle této věty jsou intervaly monotonie zásadní informací pro nalezení lokálních extrémů. Vzhledem k souvislosti monotonie s derivací je tedy nutné se věnovat nalezení intervalů, kde má funkce kladnou derivaci a intervalů, kde má funkce zápornou derivaci.
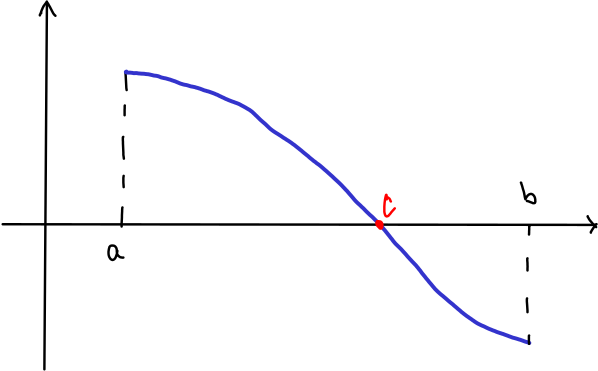
Bolzanova věta je jedna z těch, které člověka nepřekvapí. Pokud se má funkce spojitě přehoupnout z jedné strany osy na druhou, musí tuto osu někde protnout.
Bolzanova věta je poměrně názorné tvrzení. Hlavním přínosem pražského matematika Bernarda Bolzana bylo, že si uvědomil, že toto tvrzení není snadným důsledkem definice spojitosti a že přes názornost tohoto tvrzení je nutno podat jeho přesný důkaz, který rozhodně není jednoduchý. Jiná, zdánlivě nevinná tvrzení, však pravdivá být nemusí. Zde se nabízí souvislost se spojitostí funkce a nakreslitelností jedním tahem. Bolzano například našel funkci, která je spojitá, ale její graf je tak komplikovaný, že se nedá nakreslit.
Podmínka \(f(a)f(b)<0\) v následující větě znamená, že funkční hodnoty funkce \(f\) v bodech \(a\) a \(b\) se liší znaménkem.
Věta (Bolzanova věta).
Nechť \(f\) je spojitá funkce na intervalu \([a,b]\) a \(f(a)f(b)<0\). Potom existuje \(c\) na intervalu \((a,b)\) takové, že platí \(f(c)=0.\)
Důsledek.
Poznámka. Lokální extrém nastává tam, kde je funkce spojitá a kde se mění monotonie. Nenastává tam, kde se monotonie spojité funkce nemění. Přirozeně nenastává ani tam, kde funkce není definována.
Příklad. Najděte lokální extrém funkce \(y=\frac x{x^2+1}\). Derivace je \(y'=\frac{(1+x)(1-x)}{(x^2+1)^2}\).
Příklad. Najděte lokální extrém funkce \(y=\frac{x^3}{x+2}\). Derivace je \(y'=\frac{2(x+3)x^2}{(x+2)^2}\).
Řešení příkladů bude na přednášce. Další příklady ve cvičení.
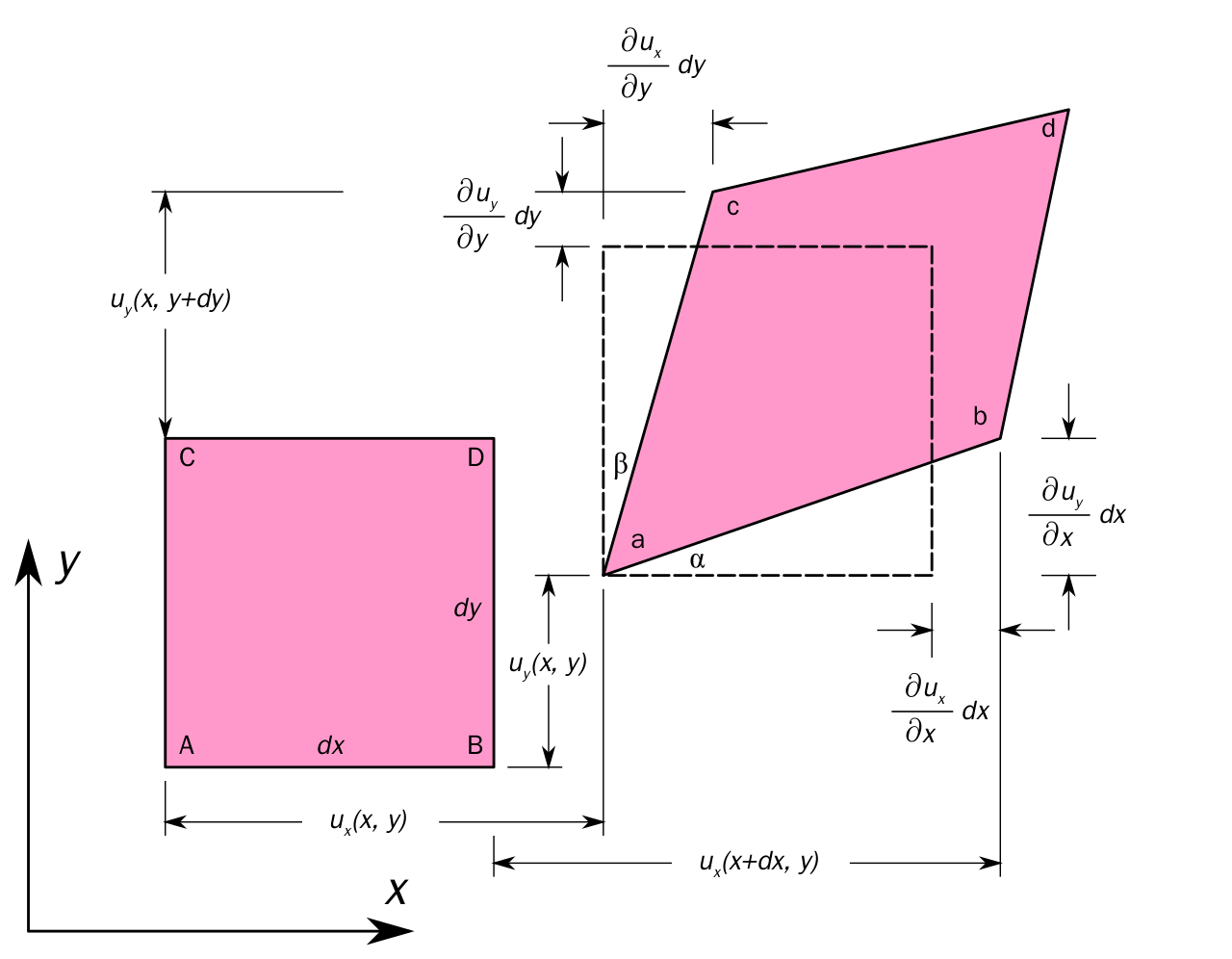
Působením síly se element materiálu může posunout, rotovat, deformovat. Tuto změnu potřebujeme zachytit. Zdroj: https://physics.stackexchange.com/questions/311716/geometric-derivation-of-the-infinitesimal-strain-tensor/311744
Následující pasáže rozšiřují lineární aproximaci na případ, kdy chceme popsat transformaci roviny. Protože v tomto případě pracujeme se dvěma souřadnicemi, je nutno uvažovat dvě funkce (pro každou souřadnici jednu funkci) a každá funkce závisí na dvou proměnných (na obou souřadnicích). Popis, který si představíme, využijeme při popisu matematického namáhání při odvození veličin, na nichž je založen obecný Hookův zákon dávající do souvislosti deformaci materiálu a působení vnější síly.
Lineární aproximaci funkce jedné proměnné můžeme zapsat ve tvaru \[f(x+\Delta x)\approx f+\frac{\mathrm df}{\mathrm dx}\Delta x,\] kde na pravé straně pro stručnost nevypisujme závislost na \(x\). Podobně můžeme zapsat lineární aproximaci pro funkci dvou proměnných \(x_{1}\) a \(x_{2}\) ve tvaru \[ f(x_{1}+\Delta x_{1}, x_{2})\approx f +\frac{\partial f}{\partial x_{1}},\qquad f(x_{1}, x_{2}+\Delta x_{2})\approx f +\frac{\partial f}{\partial x_{2}}. \]
Uvažujme nyní mechanické namáhání, kdy se těleso posunuje, rotuje a deformuje vlivem působení vnější síly a bod \((x_{1}, x_{2})\) se posune o \((u_{1}(x_{1},x_{2}),u_{2}(x_{1},x_{2})).\) Pomocí lineárních aproximací \[ \begin{aligned} u_{1}(x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2})&\approx u_{1}+\frac{\partial u_{1}}{\partial x_{1}}\Delta x_{1}+\frac{\partial u_{1}}{\partial x_{2}}\Delta x_{2}\\ u_{2}(x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2})&\approx u_{2}+\frac{\partial u_{2}}{\partial x_{1}}\Delta x_{1}+\frac{\partial u_{2}}{\partial x_{2}}\Delta x_{2} \end{aligned} \] dostáváme aproximace této transformace. Při transformaci ve \(3D\) je situace podobná, jenom jsou zde další členy od třetích souřadnic. Aby se situace nestala nepřehlednou, je klasický způsob zápisu neudržitelný. Nástroj pro přehlednou formulaci lineární aproximace dostaneme k dispozici později po probrání maticového počtu a maticového násobení. Poté budeme díky lineární aproximaci schopni zformulovat souvislost mezi deformací a působením vnější síly.
Za výše uvedenou lineární aproximaci však platíme jistou daň. Lineární zobrazení mimo jiné transformuje přímky na přímky, rovnoběžky na rovnoběžky, střed úsečky na střed úsečky. Deformaci, která tyto podmínky nesplňuje, tím pádem nemůžeme podchytit. Lineární aproximace je přesná jenom pro relativně malé deformace. Proto se také výsledný produkt, ke kterému se v průběhu semestru dopracujeme, nazývá tenzor malých deformací.

A jaká je hlavní message? Zdroj: pixabay.com