- \(f: \mathbb{R}^2\to \mathbb{R}\)
- \(z=f(x,y)\), v 3D obrázku kreslíme uspořádané trojice bodů \([x,y,z]\)
- výstupem je zpravidla plocha v prostoru
- zkusit online (Sage)
- zkusit online (matplotlib)
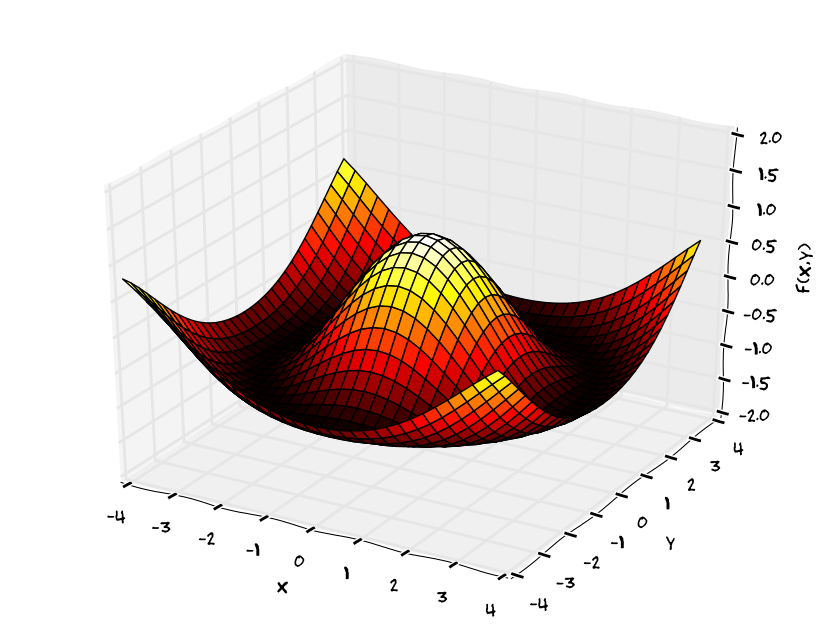
3d graf
Definice. Množina \(\mathbb{E}^n\) prvků z \(\mathbb{R}^n\) s metrikou \(\rho\) definovanou pro \(X=(x_1,x_2,\dots x_n)\in\mathbb{R}^n\) a \(Y=(y_1,y_2,\dots, y_n)\in\mathbb{R}^n\) vztahem \[ \label{eq:eukl-metrika} \rho(X,Y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\cdots+(x_n-y_n)^2} \] se nazývá Euklidovský metrický prostor. Prvky prostoru \(E^n\) budeme nazývat body. Funkce \(\rho\) se nazývá Euklidovská metrika. Číslo \(\rho(X,Y)\) se nazývá Euklidovská vzdálenost bodů \(X\), \(Y\).
V prostorech \(\mathbb{E}^2\) a \(\mathbb{E}^3\) se jedná o definici vzdálenosti, používanou v každodenním životě. I následující tři vlastnosti metriky jsou v těchto prostorech velice názorné.
Věta (vlastnosti euklidovské metriky) Pro libovolná \(X,Y,Z\in\mathbb{E}^n\) platí \[ \begin{alignat*}{2} &\rho(X,Y)=\rho(Y,X)&&\text{symetrie}\\ &\rho(X,Y)=0\iff X=Y &&\text{totožnost}\\ &\rho(X,Y)+\rho(Y,Z)\geq \rho(X,Z)\quad&&\text{trojúhelníková nerovnost} \end{alignat*} \]
Definice. Buď \(X\in \mathbb{E}^n\) bod z \(\mathbb{E}^n\) a \(\varepsilon>0\) kladné reálné číslo. Epsilonovým okolím bodu \(X\) rozumíme množinu označenou \(O_\varepsilon(X)\) skládající se z bodů, jejichž vzdálenost od bodu \(X\) je menší než \(\varepsilon\), tj. \[ O_\varepsilon(X)=\{Y\in\mathbb{E}^n:\rho(X,Y)<\varepsilon\}. \] Ryzím epsilonovým okolím bodu \(X\) rozumíme množinu \(\overline O_\varepsilon(X)\) definovanou \[ \overline O_\varepsilon(X)=O_\varepsilon(X)\setminus\{X\}, \] tj. \(\varepsilon\)-okolí bodu \(X\), s vyloučením bodu \(X\).
Definice. Množina \(M\) se nazývá ohraničená, jestliže leží v (dostatečně velkém) okolí nějakého bodu \(Y\in\mathbb{E}^n\).
Definice. Bod \(X\) se nazývá izolovaným bodem množiny \(M\), jestliže existuje okolí \(O(X)\) bodu \(X\) s vlastností \(O(X)\cap M=\{X\}\).
Definice. Bod \(X\) se nazývá hromadným bodem množiny \(M\), jestliže každé ryzí okolí bodu \(X\) obsahuje alespoň jeden bod, ležící v množině \(M\) (v tomto případě jich navíc obsahuje dokonce nekonečně mnoho).
Definice. Bod \(X\) se nazývá vnitřním bodem množiny \(M\), jestliže \(X\in M\) a existuje nějaké okolí \(O(X)\) bodu \(X\) ležící celé v množině \(M\), tj. \(O(X)\subseteq M\). Množina všech vnitřních bodů množiny \(M\) se nazývá vnitřek množiny \(M\) a označuje \(M^o\). Je-li množina \(M\) totožná se svým vnitřkem, tj. je-li každý bod množiny \(M\) vnitřní, říkáme, že množina \(M\) je otevřená.
Definice. Bod \(X\) se nazývá hraničním bodem množiny \(M\), jestliže každé okolí bodu \(X\) obsahuje alespoň jeden bod ležící v množině \(M\) a současně alespoň jeden bod neležící v množině \(M\). Množina všech hraničních bodů množiny \(M\) se nazývá hranice množiny \(M\) a označuje \(\partial M\).
Definice. Uzávěrem množiny \(M\) rozumíme množinu \(\overline M\) definovanou jako sjednocení vnitřku a hranice množiny \(M\), tj. \(\overline M=M^o\cup\partial M\). Je-li množina totožná se svým uzávěrem (tj. obsahuje-li všechny své hraniční body), nazývá se uzavřená.
Definice. Množina \(M\) se nazývá souvislá, jestliže každé dva body, ležící v množině \(M\) lze spojit lomenou čarou, ležící v \(M\).
Definice. Otevřená souvislá množina se nazývá oblast. Uzavřená souvislá množina se nazývá uzavřená oblast. Uzavřená ohraničená množina se nazývá kompaktní.
Definice. Řekneme, že pravidlo \(f\) je s \(D(f)\subseteq \mathbb{R}^n\) a \(Im(f)\subseteq \mathbb{R}\), jestliže toto pravidlo každému \(X\in D(f)\) přiřazuje jediné číslo \(Y\in Im(f)\). Píšeme \(Y=f(X)\).
Prvek \(X\) nazýváme a číslo \(Y\) . Je-li \(f\) funkce \(n\) proměnných, píšeme \(f:\mathbb{R}^n\to\mathbb{R}\).
Definice. Uvažujme funkci dvou proměnných \(f:\mathbb{R}^2\to \mathbb{R}\). Grafem funkce \(f\) rozumíme množinu bodů \((x,y,z)\in\mathbb{R}^3\) s vlastností \(z=f(x,y)\). Zpravidla touto množinou bude nějaká plocha v prostoru.
Nechť \(C\in Im(f)\) je předem dané číslo. Vrstevnicí na úrovni \(C\) rozumíme množinu všech bodů \((x,y)\in\mathbb{R}^2\), splňující \(f(x,y)=C\).

3d graf
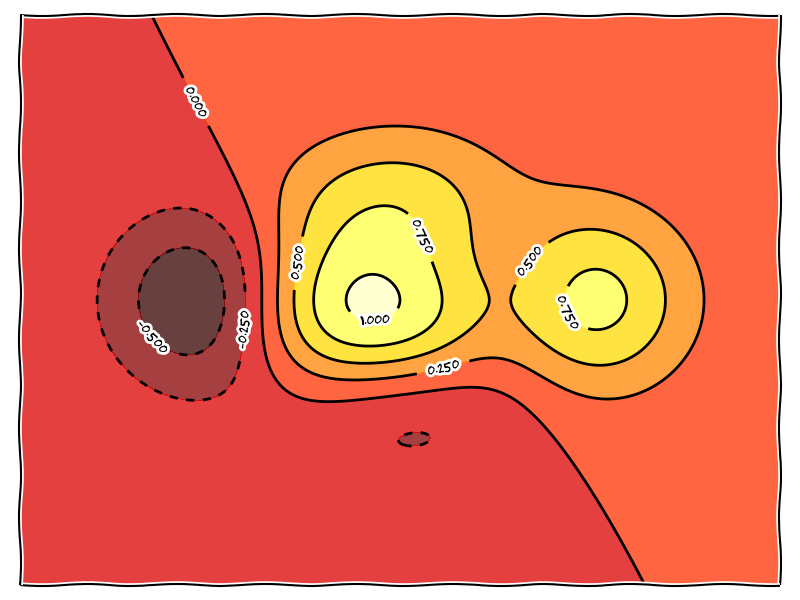
vrstevnice
Definice. Nechť \(f:\mathbb{R}^n\to \mathbb{R}\) je funkce \(n\) proměnných definovaná v nějakém ryzím okolí bodu \(A\in\mathbb{R}^n\). Řekneme, že funkce \(f\) má v bodě \(A\) limitu rovnu číslu \(L\in\mathbb{R}\), jestliže pro každé okolí \(O(L)\) bodu \(L\) existuje ryzí okolí \(\overline O(A)\) bodu \(A\) takové, že obrazy všech bodů z tohoto ryzího okolí bodu \(A\) leží v okolí bodu \(L\), tj. pro všechna \(X\in \overline O(A)\) platí \(f(X)\in O(L)\). Píšeme \[ \lim_{X\to A}f(X)=L. \]
Definice. Řekneme, že funkce \(f:\mathbb{R}^n\to \mathbb{R}\) je spojitá v bodě \(A\), jestliže
- existuje \(f(A)\), tj . funkce \(f\) je v bodě \(A\) definovaná,
- existuje \(\lim_{X\to A}f(X)\), tj. funkce \(f\) má v bodě \(A\) limitu,
- platí \(f(A)=\lim_{X\to A}f(X)\).
Řekneme, že funkce \(f:\mathbb{R}^n\to\mathbb{R}\) je spojitá na otevřené množině \(M\), je-li spojitá ve všech bodech množiny \(M\)
Definice (ekvivalentní definice spojitosti) Nechť \(f:\mathbb{R}^n\to \mathbb{R}\) je funkce \(n\) proměnných definovaná v nějakém okolí bodu \(A\in\mathbb{R}^n\). Řekneme, že funkce \(f\) je v bodě \(A\) spojitá, jestliže pro každé okolí \(O(f(A))\) bodu \(f(A)\) existuje okolí \(\overline O(A)\) bodu \(A\) takové, že obrazy všech bodů z tohoto okolí bodu \(A\) leží v okolí bodu \(O(f(A))\), tj. pro všechna \(X\in \overline O(A)\) platí \(f(X)\in O(f(A))\). \end{veta}
Věta (spojitost elementárních funkcí) Všechny mnohočleny, goniometrické, cyklometrické, exponenciální a logaritmické funkce, obecná mocnina a dále všechny funkce, které z nich získáme konečným počtem operací sčítání, odečítání, násobení, dělení a skládání těchto funkcí navzájem jsou spojité v každém vnitřním bodě svého definičního oboru.