Tepelná výměna probíhá intenzivněji při velkém rozdílu teplot, https://pixabay.com
Obyčejná diferenciální rovnice je rovnice, kde vystupuje neznámá funkce a její derivace. Setkáváme se s ní například všude tam, kde rychlost růstu nebo poklesu veličiny souvisí s její velikostí. Například rychlost s jakou se mění teplota horkého tělesa je funkcí teploty samotné. Rychlost tepelné výměny mezi dvěma tělesy je totiž úměrná rozdílu jejich teplot (Newtonův zákon).
Definice (diferenciální rovnice).
Obyčejnou diferenciální rovnicí prvního řádu rozřešenou vzhledem k derivaci (stručněji též diferenciální rovnicí, DR) s neznámou \(y\) rozumíme rovnici tvaru \[ y'=\varphi(x,y) \tag{ODE}\] kde \(\varphi\) je funkce dvou proměnných.
(anglicky ordinary differential equation, ODE)
Další formy zápisu: \[\frac{\mathrm{d}y}{\mathrm{d}x}=\varphi(x,y)\] \[{\mathrm{d}y}=\varphi(x,y)\mathrm{d}x\] \[{\mathrm{d}y}-\varphi(x,y)\mathrm{d}x=0\]
Příklad: Najděte všechny funkce splňující \(y'=2xy\).
Diferenciální rovnice udává scénář vývoje systému. K jednoznačnému předpovězení budoucího stavu je ovšem nutno znát nejenom, jaký mechanismus ovlivňuje vývoj systému, ale také stav současný.
Definice (počáteční podmínka, počáteční úloha).
Nechť \(x_0\), \(y_0\) jsou reálná čísla. Úloha najít řešení rovnice
\[ y'=\varphi(x,y), \tag{ODE}\] které splňuje zadanou počáteční podmínku \[ y(x_0)=y_0 \tag{IC}\] se nazývá počáteční (též Cauchyova) úloha.Řešení Cauchyovy úlohy nazýváme též partikulárním řešením rovnice. Graf libovolného partikulárního řešení se nazývá integrální křivka.
(anglicky initial condition, IC, initial value problem, IVP)
Příklad: Najděte všechny funkce splňující \(y'=2xy\) a \(y(0)=3\).
Tepelná výměna probíhá intenzivněji při velkém rozdílu teplot, https://pixabay.com
Rovnice konstantního růstu nebo úbytku je základem datování pomocí uhlíku, https://www.flickr.com/photos/capturetheuncapturable, licence CC BY 2.0
Při operaci ztrácí pacient krvinky rychlostí úměrnou koncentraci krvinek, https://pixabay.com
Jezero, ve kterém se přirozeně obměňuje znečištěná voda za čistou, se dokáže samo zotavit ze znečištění. Rychlost vyplavování nečistot je úměrná míře znečištění. https://pixabay.com
Při intenzivním lovu může dojít ke zničení populace https://pixabay.com
Za uvedených předpokladů je možno vývoj populace popsat rovnicí \[\frac{\mathrm dy}{\mathrm dt}=ry\left(1-\frac yK\right).\]
Pokud lovem snížíme přírůstky populace, můžeme tento proces modelovat rovnicí \[\frac{\mathrm dy}{\mathrm dt}=ry\left(1-\frac yK\right)-h(y),\] kde \(h(y)\) je intenzita lovu populace o velikosti \(y\). Modelování tohoto procesu umožní nalezení ekonomicky výhodné ale trvale udržitelné strategie lovu.
Protože derivace funkce v bodě udává směrnici tečny ke grafu funkce v tomto bodě, lze rovnici \[y'=\varphi(x,y)\tag{ODE}\] chápat jako předpis, který každému bodu v rovině přiřadí směrnici tečny k integrální křivce, která tímto bodem prochází. Sestrojíme-li v dostatečném počtu (například i náhodně zvolených) bodů \([x,y]\) v rovině vektory \((1,\varphi(x,y))\), obdržíme směrové pole diferenciální rovnice — systém lineárních elementů, které jsou tečné k integrálním křivkám.
Počáteční podmínka \(y(x_0)=y_0\) geometricky vyjadřuje skutečnost, že graf příslušného řešení prochází v rovině bodem \([x_0,y_0]\). Má-li tato počáteční úloha jediné řešení, neprochází bodem \([x_0,y_0]\) žádná další křivka. Má-li každá počáteční úloha jediné řešení (což bude pro nás velice častý případ), znamená to, že integrální křivky se nikde neprotínají.
Vrstevnice funkce \(\varphi(x,y)\) mají tu vlastnost, že derivace integrálních křivek podél každé z vrstevnic je konstantní. Proto tyto křivky nazýváme isokliny.
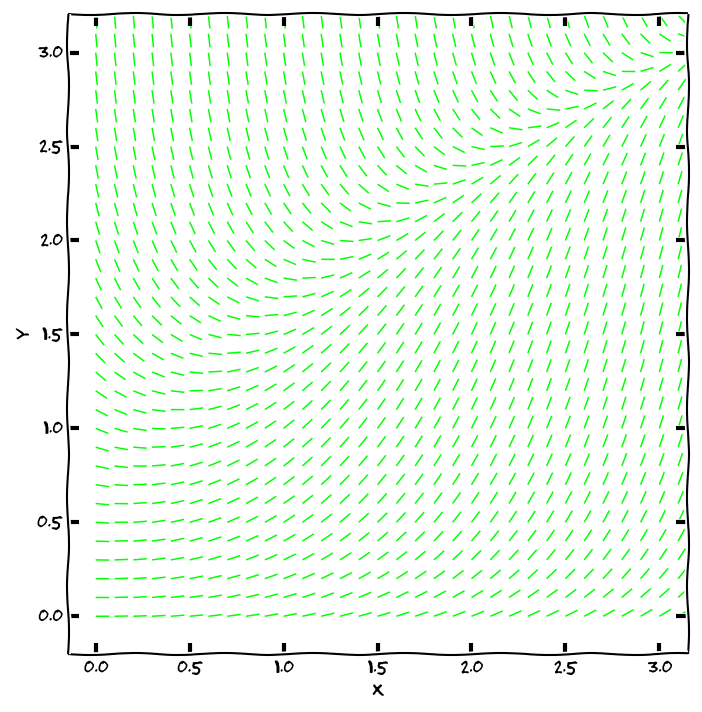
Směrové pole diferenciálni rovnice
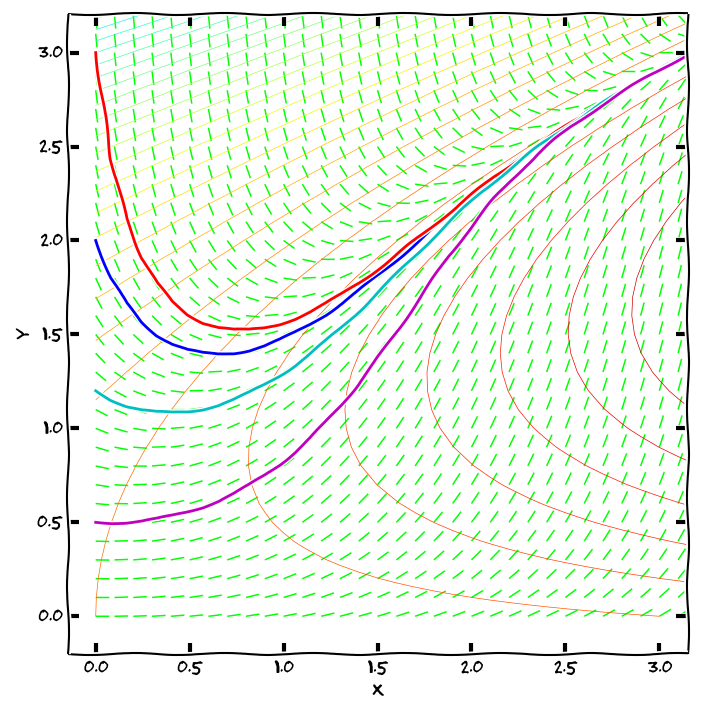
Směrové pole diferenciálni rovnice, integrální křivky, isokliny
Řešení diferenciální rovnice je nekonečně mnoho. Zpravidla je dokážeme zapsat pomocí jediného vzorce, který obsahuje nějakou (alespoň do jisté míry libovolnou) konstantu \(C\). Takový vzorec se nazývá obecné řešení rovnice. Pokud není zadána počáteční podmínka a mluvíme o partikulárním řešení, máme tím na mysli jednu libovolnou funkci splňující diferenciální rovnici.
Příklad: Obecným řešením diferenciální rovnice \[y'=2xy\] je \[y=Ce^{x^2}, \quad C\in\mathbb{R}.\] Žádná jiná řešení neexistují, všechna řešení se dají zapsat v tomto tvaru pro nějakou vhodnou konstantu \(C\). Partikulárním řešením je například \(y=5e^{x^2}\). Řešením počáteční úlohy \[y'=2xy, \quad y(0)=3\] je \[y=3e^{x^2}.\]
Online řešiče ODE (symbolicky):
Řešení počáteční úlohy lze numericky aproximovat poměrně snadno: začneme v bodě zadaném počáteční podmínkou a v okolí tohoto bodu nahradíme integrální křivku její tečnou. Tím se dostaneme do dalšího bodu, odkud opět integrální křivku aproximujeme tečnou. Směrnici tečny zjistíme z diferenciální rovnice, buď přímo z derivace (Eulerova metoda).
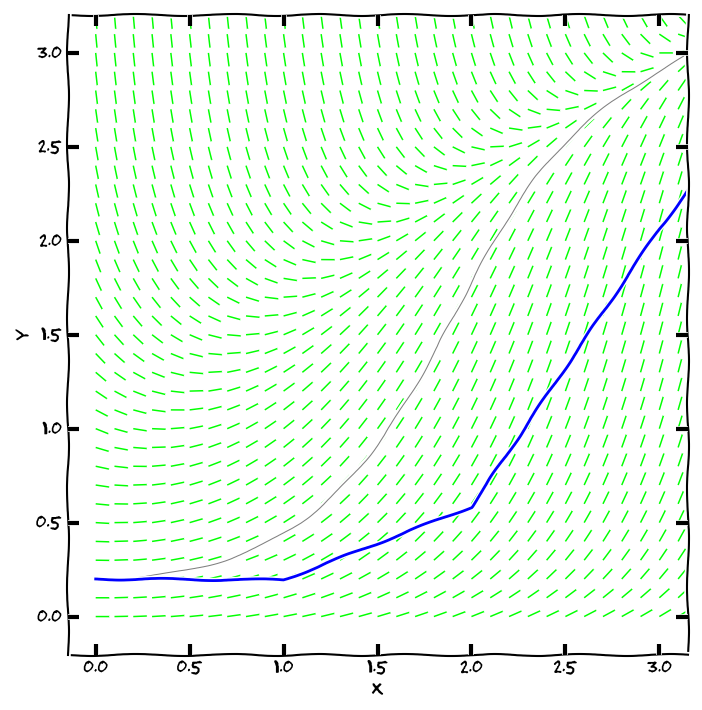
Další možnost je použít k aproximaci sečnu tak, že opravíme směrnici tečny podle chování směrového pole. Bereme v úvahu i konvexnost či konkávnost a fakt, že se derivace mění s měnícím se \(x\) i \(y\) (metoda Runge–Kutta). Stačí tedy mít zvolen krok numerické metody (délku intervalu, na kterém aproximaci tečnou použijeme) a výstupem metody bude aproximace integrální křivky pomocí lomené čáry.
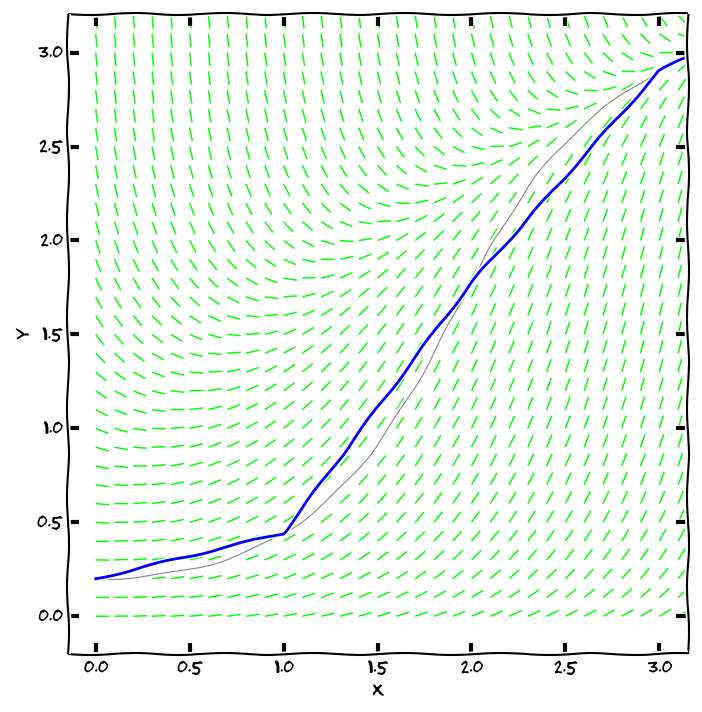
Metoda Runge Kutta s velmi dlouhým krokem (modrou barvou, jde jasně vidět aproximace lomenou čarou). Přesné řešení je nakresleno šedou barvou.
Počáteční úloha: \[y'=\varphi(x,y), \quad y(x_0)=y_0\]
Tečna k řešení v bodě \([x_0,y_0]\): \[y=y_0+\varphi(x_0,y_0)(x-x_0).\]
Funkční hodnota v bodě \(x_0+h\), kde \(h\) je krok Eulerovy metody: \[y(x_0+h)=y_0+\varphi(x_0,y_0)h.\]
Iterační formule Eulerovy metody: \[\begin{aligned}x_{n+1}&=x_n+h, \\ y_{n+1}&=y_n+\varphi(x_n,y_n)h.\end{aligned}\]
Vylepšení
Eulerova metoda s velmi dlouhým krokem (modrou barvou) zaostává za přesným řešením (šedou barvou). Pro lepší výsledek můžeme zmenšit krok nebo vylepšit metodu.
Součást protiraketového systému Patriot. Raketu Scud vystřelenou 25.2.1991 systém nesestřelil vinou zaokrouhlovací chyby. Zdroj: U.S. Army.
Uvedli jsme, že počáteční úlohu umíme vyřešit numericky. Ukázali jsme si základní algoritmus (Eulerův) a řekli, že existují algoritmy pokročilejší. Na tomto místě upozorníme na záludnosti skryté v numerických výpočtech. Je iluzorní se domnívat, že zjemněním kroku při numerickém řešení diferenciální rovnice vždy dostaneme přesnější řešení. Toto platí jenom dokud se nedostaneme ke kritické hodnotě kroku, kdy další snižování vede k tomu, že zpřesnění díky kratšímu kroku se přebije akumulovanou chybou z velkého množství výpočtů nutně zatížených zaokrouhlováním a dalším zjemňováním přesnost ztrácíme.
Zajímavá léčka je v samé podstatě výpočtů na počítači a to v reprezentaci desetinných čísel ve dvojkové soustavě. Například číslo 0.1 je ve dvojkové soustavě periodické! Proto desetinásobným sečtením tohoto čísla ve dvojkové soustavě nedostaneme (překvapivě) jedničku! Je to podobné, jako bychom v námi běžně používané dvojkové soustavě třikrát sečetli jednu třetinu v desetinném tvaru reprezentovaném konečným počtem desetinných míst, tj. například třikrát sečetli číslo \(0.33333333\). Nedostaneme přesně jedničku.
Tento efekt měl i tragický důsledek. Software protiraketového systému Patriot počítal čas postupným přičítáním desetiny sekundy. Protože systém byl vytvořen a testován na mobilním zařízení, které se často restartovalo a běželo krátkou dobu, ničemu to nevadilo. Nasazení v systému Patriot však byla chyba. Při ostrém nasazení systém běžel dlouho, zaokrouhlovací chyba se kumulovala například 100 hodin. I když za tu dobu chyba dosáhla pouze zlomku sekundy, raketa letící vysokou rychlostí již byla jinde, než systém Patriot propočítal. Dne 25.2.1991 systém Patriot během operace Pouštní bouře na osvobození Kuvajtu od irácké okupace nesestřelil útočící raketu Scud a ta zabila 28 vojáků osvobozující armády a okolo 100 osob zranila.
S chybami plynoucími ze zaokrouhlování se setkáme i při výpočtech mimo modelování diferenciálních rovnic. Viz například Floating-point arithmetic may give inaccurate results in Excel.
Definice (separovatelná diferenciální rovnice).
Diferenciální rovnice tvaru \[ y'=f(x)g(y) \tag{S}\] kde \(f\) a \(g\) jsou funkce spojité na (nějakých) otevřených intervalech se nazývá obyčejná diferenciální rovnice se separovanými proměnnými.
Příklad: Rovnice \[y'+xy +xy^2=0\] je rovnicí se separovanými proměnnými, protože je možno ji zapsat ve tvaru \[y'=-xy(y+1).\] Rovnice \[y'=x^2-y^2\] není rovnice se separovatelnými proměnnými.
Test separovatelnosti proměnných: Diferenciální rovnice \[y'=\varphi(x,y)\] je rovnicí se separovanými proměnnými právě tehdy, když existují funkce \(f(x)\) a \(g(y)\) takové, že \[\varphi(x,y)=f(x)g(y). \] Pokud je \(\varphi\) nezáporná a dostatečně hladká na nějaké otevřené konvexní množině, je rovnice rovnicí se separovanými proměnnými právě tehdy, když platí \[\begin{vmatrix}\varphi&\frac{\partial}{\partial x}\varphi\\ \frac{\partial}{\partial y}\varphi&\frac{\partial^2}{\partial x\partial y}\varphi \end{vmatrix}=0.\]
Má-li algebraická rovnice \(g(y)=0\) řešení \(k_1\), \(k_2\), …, \(k_n\), jsou konstantní funkce \(y\equiv k_1\), \(y\equiv k_2\), …, \(y\equiv k_n\) řešeními rovnice.
Pracujme na intervalech, kde \(g(y)\neq 0\). Formálně nahradíme derivaci \(y'\) podílem diferenciálů \(\frac{\mathrm{d}y}{\mathrm{d}x}\) \[ \frac{\mathrm{d}y}{\mathrm{d}x}=f(x)g(y).\]
Odseparujeme proměnné \[ \frac{\mathrm{d}y}{g(y)}=f(x)\mathrm{d}x.\]
Získanou rovnost integrujeme \[ \int \frac{\mathrm{d}y}{g(y)}=\int f(x)\mathrm{d}x+C.\]
Pokud je zadána počáteční podmínka, je možné ji na tomto místě dosadit do obecného řešení a určit hodnotu konstanty \(C\). Tuto hodnotu poté dosadíme zpět do obecného řešení a obdržíme řešení partikulární.
Pokud je to možné, převedeme řešení (obecné nebo partikulární) do explicitního tvaru (vyjádříme odsud \(y\)).
Výraz \(\frac{\mathrm{d}y}{\mathrm{d}x}\) je derivace, nikoliv podíl, proto je s podivem, že výše uvedený postup funguje. Berme jej prosím jako mnemotechinckou pomůcku při řešení a představme si sofistikovanější zdůvodnění tohoto postupu (pro případ \(g(y)\neq 0\)) založené na integrování a substituci v neučitém integrálu.
\[ \begin{aligned} y'&=f(x)g(y)\\ \frac{1}{g(y)} y' &= f(x) \\ \int \frac{1}{g(y(x))} y'(x)\mathrm{d}x &= \int f(x) \mathrm{d}x\\ \int \frac{1}{g(y)} \mathrm{d}y &= \int f(x) \mathrm{d}x \end{aligned} \]
Za povšimnutí také stojí fakt, že ekvivalentní vyjádření rovnice ve tvaru \[ f(x)\mathrm{d}x - \frac{1}{g(y)} \mathrm{d}y = 0 \] obsahuje na levé straně totální diferenciál. Kmenová funkce tohoto diferenciálu je \[F(x,y)= \int f(x) \mathrm{d}x - \int \frac{1}{g(y)} \mathrm{d}y \] a řešení rovnice jsou tvaru \[F(x,y)=C, \qquad C\in\mathbb{R}.\] Pohlížíme-li na tento vztah jako na implicitně zadanou funkci a počítáme-li pomocí aparátu funkce dvou proměnných derivaci této funkce, dostaneme přesně vztah \[ y'=f(x)g(y). \]
Věta (o existenci a jednoznačnosti řešení).
Je-li \(g(y_0)\neq 0\), je řešení počáteční úlohy \[y'=f(x)g(y), \qquad y(x_0)=y_0,\] které obdržíme pomocí postupu z předchozích odstavců, definované a jednoznačně určené v nějakém okolí bodu \(x_0\).
Vzorec pro řešení IVP pro rovnici se separovatelnými proměnnými: Partikulární řešení počáteční úlohy \[y'=f(x)g(y), \qquad y(x_0)=y_0\] lze psát též přímo ve tvaru určitého integrálu \[\int_{y_0}^y\frac {\mathrm{d}t}{g(t)}=\int_{x_0}^x f(t)\mathrm{d}t.\]
Londýnská mlha. Dnes už to není jako za časů Sherloka Holmese. Poslední velká mlha (Pea soup fog) byla v roce 1952. Zdroj: Wikipedia.
Modelujme růst kulové kapky. Ta roste tak, že na povrchu kondenzují vodní páry. Kapka proto roste tak, že její objem se zvětšuje rychlostí úměrnou povrchu. Povrch je zase úměrný druhé mocnině poloměru a poloměr je úměrný třetí odmocnině objemu. Platí tedy (po sloučení všech konstant úměrnosti do jedné) \[\frac{\mathrm dV}{\mathrm dt}=kV^{2/3}.\]
Tato rovnice má konstantní řešení \(V=0\). Nekonstantní řešení dostaneme po úpravě \[V^{-2/3}\mathrm dV=k\mathrm dt\] a po integraci \[\int V^{-2/3}\mathrm dV=k\int \mathrm dt,\] což dává \[3V^{1/3}=kt+C\] a \[V=\left(\frac 13 kt+ \frac 13 C\right)^3,\] tj. \[V=\left(k_0t+ c\right)^3,\] kde \(k_0=\frac 13 k\) a \(c=\frac 13 C\) jsou konstanta spojená rychlostí kondenzace a integrační konstanta.
Všimněte si, že počáteční úloha s počáteční podmínkou \(V(0)=0\) má konstantní nulové řešení \[V(t)=0\] a nenulové řešení \[V(t)=(k_0t)^3.\] Máme zde tedy nejednoznačnost v řešení počáteční úlohy. Tato nejednoznačnost není v rozporu s větou o existenci a jednoznačnosti řešení, protože pravá strana diferenciální rovnice nemá ohraničnou derivaci podle \(V\). A nejednoznačnost má v tomto případě dokonce fyzikální význam. Plynné skupenství může existovat i pod bodem kondenzace. Takovému jevu se říká přechlazená pára. Aby došlo ke kondenzaci, musí být k dispozici kondenzační jádra, například nečistoty ve vzduchu. Proto ve znečištěném ovzduší dochází častěji ke kondenzaci a tvorbě mlhy. Své by o tom mohli vyprávět obyvatelé Londýna, kteří se proslulých mlh zbavili poté, co se omezilo topení uhlím. My dnes spíše známe přechlazenou tekutinu ve formě hřejících polštářků, kde se po lupnutí plíškem spustí přeměna skupenství na pevné spojená s intenzivním uvolněním tepla.