Lineární autonomomní systémy s konstatními koeficienty

Viz přednáška a jiné materiály

Obecné autonomní systémy

Viz přednáška a jiné materiály

Aproximace derivací pomocí konečných diferencí

Z aproximace Taylorovým polynomem druhého řádu napsaného pro $f(x+h)$ a $f(x-h)$, tj. ze vztahů $$\begin{aligned} f(x+h)&\approx f(x)+f'(x)h+\frac 12 f''(x)h^2\\ f(x-h)&\approx f(x)-f'(x)h+\frac 12 f''(x)h^2 \end{aligned}$$ plyne (pokud tyto vztahy sečteme a odečteme) $$\begin{aligned} f(x+h)+f(x-h)&\approx2f(x)+ f''(x)h^2\\ f(x+h)-f(x-h)&\approx2f'(x)h. \end{aligned}$$ Odsud dostáváme aproximace první derivace pomocí centrální diference
$$\frac{\mathrm d f}{\mathrm dx}=f'(x)\approx \frac{f(x+h)-f(x-h)}{2h}$$ a aproximaci druhé derivace $$\frac{\mathrm d^2f}{\mathrm dx^2}=f''(x)\approx \frac{f(x-h)-2f(x)+f(x+h)}{h^2}.$$

Pro parciální derivace analogicky $$\begin{aligned} \frac {\partial ^2 f}{\partial x^2}&\approx \frac{1}{h^2}[f(x+h,y)-2f(x,y)+f(x-h,y)]\\ \frac {\partial ^2 f}{\partial y^2}&\approx \frac{1}{h^2}[f(x,y+h)-2f(x,y)+f(x,y-h)] \end{aligned}$$

Metoda konečných diferencí

Rozložení teploty na tepelně vodivé desce je možné přibližně zkoumat metodami lineární algebry. A až na některé triviální případy jinou možnost vlastně nemáme, protože přesné řešení rovnice vedení tepla je v prakticky zajímavých případech nereálné. Podobně to je s mechanickým namáháním nebo transportem látek porézním prostředím.

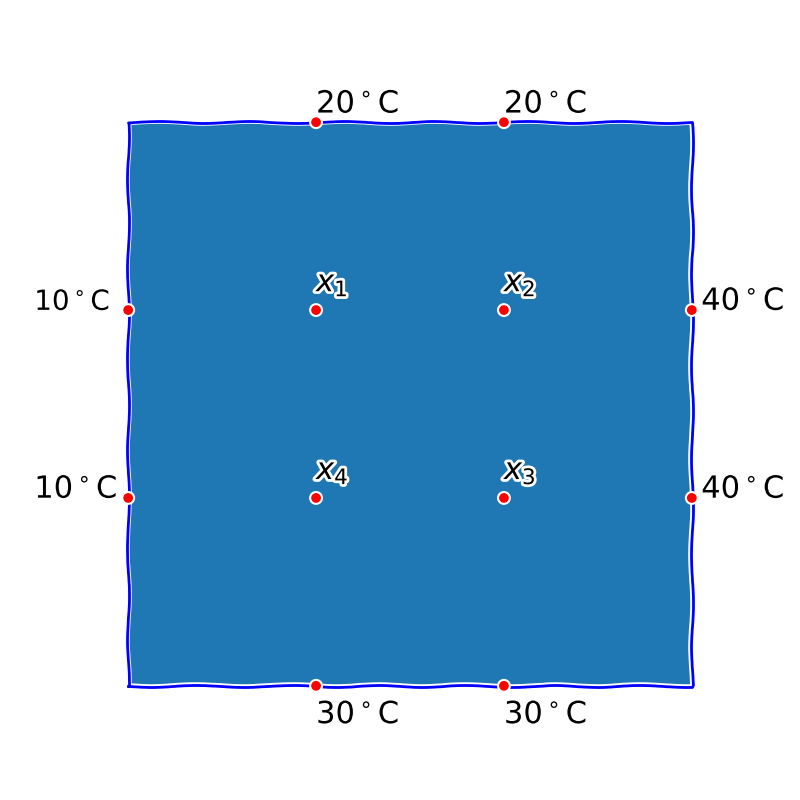
Uvažujme čtvercovou desku se zadanými teplotami na okrajích a budeme hledat rozložení teploty ve stacionárním stavu. Pro potřeby přibližného řešení si desku rozdělíme sítí na $12$ uzlových bodů (rohy zanedbáme) jak je uvedeno na obrázku, ale šlo by to i jemněji. V uzlových bodech na okraji desky je teplota zadána (okrajová podmínka), zajímá nás rozložení teploty v ostatních uzlových bodech.

Dvourozměrná rovnice vedení tepla pro homogenní izotropní desku s materiálovými charakteristikami $\rho$, $c$ a $D$ má tvar $$\rho c \frac{\partial T}{\partial t}=D\frac{\partial^2 T}{\partial x^2}+D\frac{\partial^2 T}{\partial y^2}.$$ Ve stacionárním stavu se teplota nemění s časem a proto je levá strana nulová a rovnice se redukuje na $$\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}=0.$$

Rozdělíme desku čtvercovou sítí na malé oblasti a budeme studovat teplotu v bodech této sítě, tj. v rozích jednotlivých čtverců, na které je deska čtvercovou sítí rozdělena.

Podle aproximace z předchozího slidu dostáváme $$\frac {\partial ^2 T}{\partial x^2} + \frac {\partial ^2 T}{\partial y^2} \approx \frac{1}{h^2}[T(x+h,y)+T(x-h,y)+T(x,y+h)+T(x,y-h)-4T(x,y)].$$ Z rovnice $$\frac {\partial ^2 T}{\partial x^2} + \frac {\partial ^2 T}{\partial y^2} =0,$$ popisující rozložení teploty vyplývá, že výraz v hranaté závorce musí být nulový, tj. $$T(x,y)=\frac 14 [T(x+h,y)+T(x-h,y)+T(x,y+h)+T(x,y-h)].$$ To však znamená, že teplota v každém uzlovém bodě je průměrem teplot v okolních uzlových bodech. Přesně, jak bývá (možná poněkud naivně) často zmiňováno v učebnicích lineární algebry. Nyní tento postup stavíme na solidní vědecký základ, založený na rovnici popisující fyzikální proces (rovnice vedení tepla) a na numerické aproximaci, která převede parciální diferenciální rovnici na soustavu lineárních rovnic.

Obrázek z demonstračního souboru programu FlexPDE (Lite verze zdarma) řeší rovnici pro podzemní vodu ve stacionárním stavu (div(k*grad(h)) + s = 0) za přítomnosti dvou studní a jednoho zasakovacího vrtu v nehomogenním prostředí.

Výše popsaná myšlenka je základem metody konečných diferencí. Bohužel je tato metoda poměrně omezená nutností, mít ekvidistantní rozložení uzlů. Proto se v praxi používají vyspělejší metody, metoda konečných prvků nebo metoda konečných objemů. Základní myšlenka je stejná (parciální diferenciální rovnice se převede na soustavu lineárních rovnic) a praktické provedení zpravidla matematicky triviální, protože vše potřebné pro výpočty je předprogramováno v softwaru určenému pro danou úlohu. Máme takto software umožňující simulovat vedení tepla, tepelné úniky, tepelné nebo mechanické namáhání, tok podzemní i povrchové vody a další důležité praktické aplikace. Uživatel jenom zadá geometrii, typ problému a okrajové a počáteční podmínky a program vypočte potřebná řešení a dle požadavků je různým způsobem interpretuje.

Ukázka programu FlexPDE

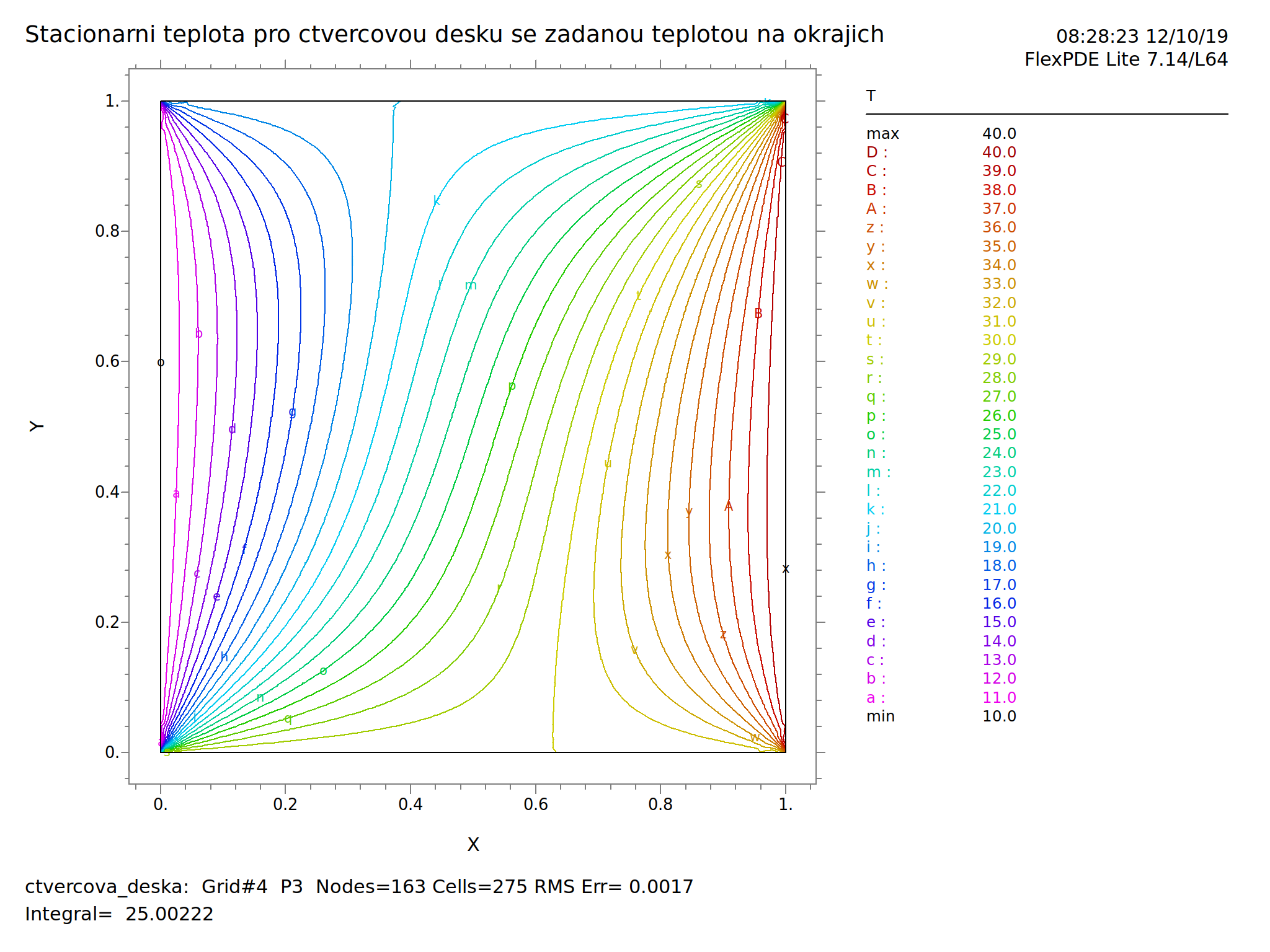
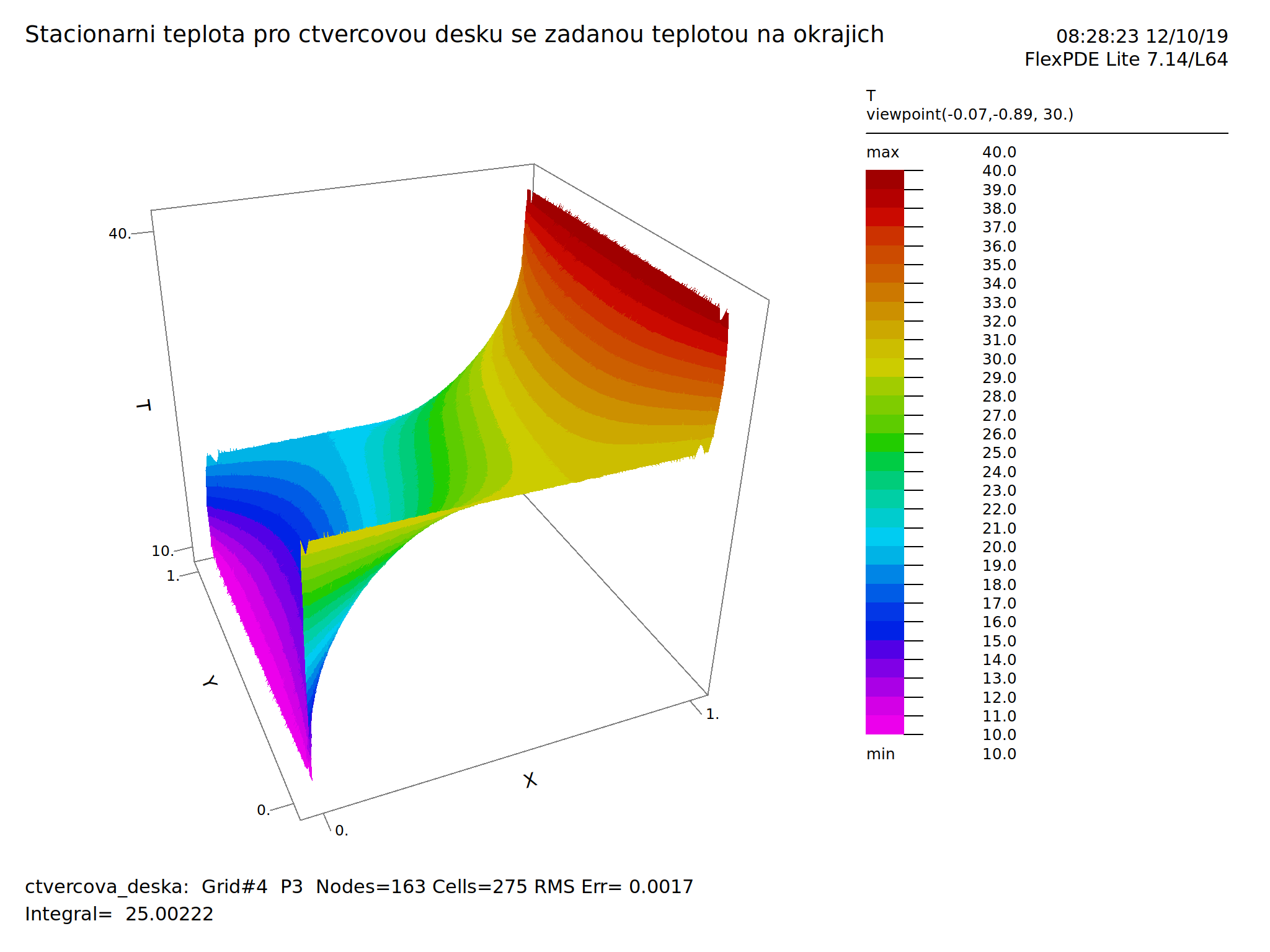
Existuje široká škála programů pro řešení diferenciálních rovnic. V mnoha jsou předpřipravené modely, předdefinované fyzikální úlohy a někdy dokonce databáze materiálových vlastností. V jiných programech je řešená rovnice plně pod kontrolou autora modelu a je možné snadno řešit i multifyzikální úlohy (například současně modelovat teplotu a vlhkost v materiálu). Zástupce druhé skupiny je FlexPDE firmy PDE Solutions Inc. Úloha s rozložením tepoty na čtvercové desce se zadanými teplotami na okrajích, na kterou jsmě několikrát jako na motivaci narazili v lineární algebře a připomněli na předchozím slidu, by měla následující zápis a výstup.

TITLE 'Stacionarni teplota pro ctvercovou desku se zadanou teplotou na okrajich' 
VARIABLES T 
EQUATIONS T: div(grad(T))=0
INITIAL VALUES T=10

BOUNDARIES
REGION 1
    START(0,0) VALUE(T)=30 LINE TO (1,0) 
    VALUE(T)=40 LINE TO (1,1)
    VALUE(T)=20 LINE TO (0,1) 
    VALUE(T)=10 LINE TO CLOSE 

PLOTS
  CONTOUR(T)
  SURFACE(T)
END

Rovnice je v popisu modelu zadána jako divergence gradientu, což v kartézských souřadnicích ve 2D vede právě na rovnici $$\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}=0.$$ Jiná forma zápisu je přímo pomocí druhých parciálních derivací ve tvaru DXX(T)+DYY(T)=0.

Teplota znázorněná pomocí izoterm.

Teplota znázorněná pomocí barev a 3D grafu.

Iterační metody pro řešení soustav lineárních rovnic

Zbývá se zabývat úlohou, jak řešit soustavu rovnic s velkým počtem neznámých. Zde není možné použít klasickou eliminační metodu, ale používají se zpravidla numerické iterační metody.

Řešení soustavy rovnic $$AX=B$$ můžeme formálně pomocí inverzní matice zapsat jako $$X=A^{-1}B.$$ Tento postup je však nerealizovatelný v praxi, porotže výpočet inverzní matice je nestabilní a výpočetně drahý. Co je snadné, je najít inverzní matici k matici diagonální. Můžeme tedy matici $A$ rozdělit na součet diagonální matice $D$ a nediagonální matice $N$ a psát $$\begin{aligned}AX&=B\\(D+N)X&=B\\DX+NX&=B\\DX&=B-NX\\X&=D^{-1}(B-NX).\end{aligned}$$

V úlohách, kde je matice $A$ řádkově ostře diagonálně dominantní (každý řádek má v hlavní diagonále číslo, které je v absolutní hodnotě větší než je součet absolutních hodnot zbylých čísel v tomto řádku) je možné matici $X$ najít tak, že začneme od libovolného odhadu řešení a používáme opakovaně iterační vzorec $$X_{k+1}=D^{-1}(B-NX_k)$$ dokud dvě po sobě jdoucí iterace $X_k$ a $X_{k+1}$ nejsou dostatečně blízké. Tento postup se nazývá Jacobiho iterační metoda. Například naše deska je popsána soustavou rovnic $$\begin{aligned} x_1&=\frac 14(30+x_2+x_4)\\ x_2&=\frac 14(60+x_1+x_3)\\ x_3&=\frac 14(70+x_2+x_4)\\ x_4&=\frac 14(40+x_1+x_3) \end{aligned}\tag{1}$$ anebo po úpravě $$\begin{aligned} 4x_1-x_2-\qquad x_4&=30\\ -x_1+4x_2-x_3\qquad&=60\\ \qquad-x_2+4x_3-x_4&=70\\ -x_1\qquad-x_3+4x_4&=40. \end{aligned}$$

Numerické řešení Jacobiho metodou vyjde z počáteční aproximace a opakovaně nahrazuje hodnotu teploty v uzlovém bodě průměrem okolních teplot. Tuto metodu je možné snadno naprogramovat a dokonce i vylepšit (Gaussova-Seidelova metoda).

Sage