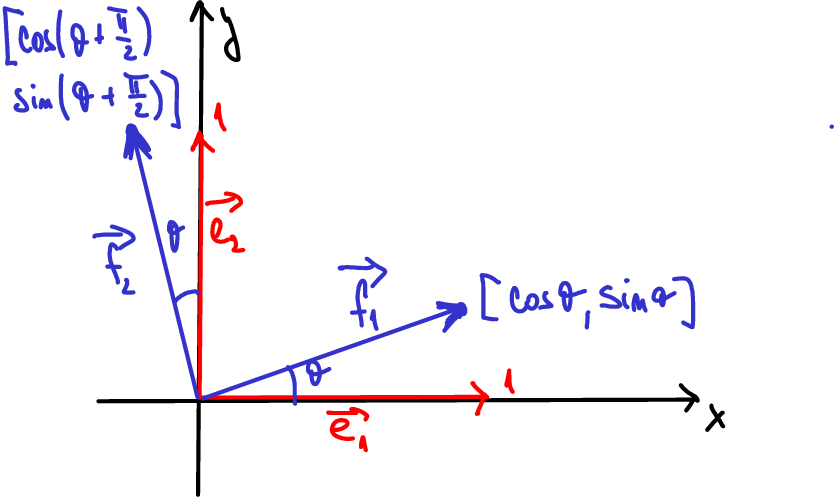
Příklad transformace dané maticí. Otočení o úhel \(\theta\).
Budeme používat jenom speciální případ násobení čtvercové matice se sloupcovou maticí (vektorem) a čtvercových matic stejného rozměru.
Násobení matice \(A=(a_{ij})\in \mathbb R^{n\times n}\) a sloupcového vektoru \(u=(u_i)^T\in\mathbb R^n\), výsledkem je sloupcový vektor \(v=(v_i)^T\in\mathbb R^n\), kde \(v_i=\sum_{i=1}^n a_{ij} u_j\).
Příklad. \[ \begin{pmatrix}2&3&1\\1&3&2\\1&-1&0\end{pmatrix} \begin{pmatrix}2\\5\\7\end{pmatrix} =\begin{pmatrix}2\cdot 2+3\cdot 5+1\cdot 7\\1\cdot 2+3\cdot 5+2\cdot 7\\1\cdot 2-1\cdot 5+0\cdot 7\end{pmatrix} =\begin{pmatrix}26\\31\\-3\end{pmatrix} \]
Násobení dvou čtvercových matic můžeme chápat jako násobení první matice se sloupcovými vektory druhé matice, výsledné součiny zapisujeme opět jako sloupce jedné matice.
Poznámka (vlastnosti maticového součinu).
- \(A(u+v)=Au+Av\) (distributivní zákon).
- \(A(\lambda u)=\lambda Au\) pro \(\lambda\in\mathbb R\) (částečná komutativita při násobení reálým číslem)
- Obecně neplatí \(AB=BA\).
- Platí \((AB)C=A(BC)\) (asociativní zákon).
- Matice \(I=(\delta_{ij})\), kde \(\delta_{ii}=1\) a \(\delta_{ij}=0\) pro \(i\neq j\) splňuje \(AI=IA=A\) (jednotková matice).
Uspořádané \(n\)-tice můžeme chápat jako vektory nebo jako body. Potom má maticový součin následující využití.

Příklad transformace dané maticí. Otočení o úhel \(\theta\).
Je-li \(A\) čtvercová matice, můžeme každému vektoru \(\vec q\) přiřadit vektor \(Y=A\vec q\) a tím definovat zobrazení \(n\)-rozměrného prostoru do sebe. Dá se ukázat, že takto dostaneme všechna zobrazení, která zobrazují úsečky na úsečky, počátek nechávají v počátku a jsou pěkná v tom smyslu, že zachovávají středy úseček, rovnoběžnost a lineární kombinaci vektorů. Ukázka zobrazení ve 2D.
Například matice \[R_\theta= \begin{pmatrix} \cos\theta & \cos \left(\theta+\frac \pi 2\right)\\ \sin\theta & \sin \left(\theta+\frac \pi 2\right) \end{pmatrix} = \begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix} \] zobrazí vektory \(e_1=(1,0)\) a \(e_2=(0,1)\) na \[\begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} 1\\0 \end{pmatrix} = \begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix} \] a \[\begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} 0\\1 \end{pmatrix} = \begin{pmatrix} -\sin\theta \\ \cos\theta \end{pmatrix}. \] Proto matice \(R_\theta\) definuje zobrazení, které pootočí rovinu o úhel \(\theta\) a nazývá se matice rotace. Matice malých rotací je (použitím lineární aproximace \(\sin\theta\approx \theta\) a \(\cos \theta\approx 1\) v okolí nuly) \[R_{\theta,0}= \begin{pmatrix} 1 & - \theta\\ \theta & 1 \end{pmatrix}. \] Tuto matici budeme potřebovat při studiu deformace při odvození matematického popisu malých deformací.
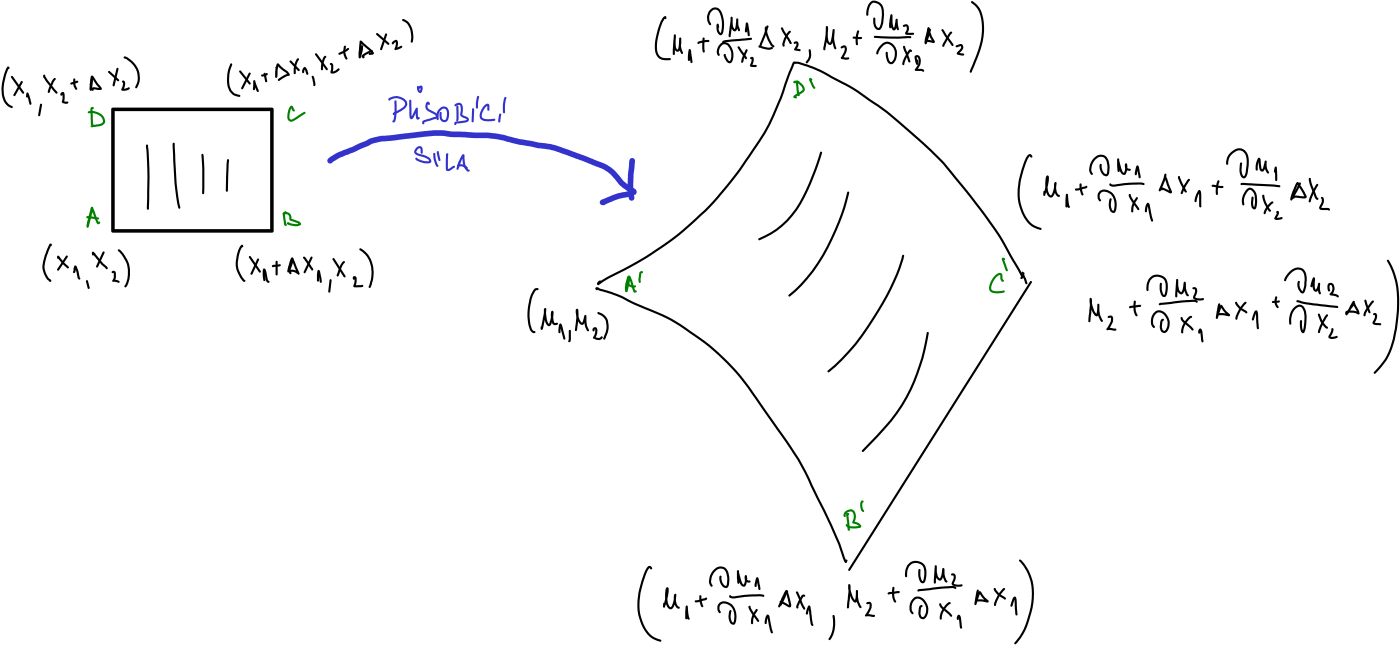
Působením síly se element materiálu může posunout, rotovat, deformovat. Tunto změnu potřebujeme zachytit.
Uvažujme nyní mechanické namáhání, kdy se těleso posunuje, rotuje a deformuje vlivem působení vnější síly a bod \((x_{1}, x_{2})\) se transformuje na bod \((u_{1}(x_{1},x_{2}),u_{2}(x_{1},x_{2})).\) Čtverec \(ABCD\) na obrázku se zobrazí na obrazec \(A'B'C'D'\). Pomocí lineárních aproximací můžeme psát \[ \begin{aligned} u_{1}(x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2})&\approx u_{1}+\frac{\partial u_{1}}{\partial x_{1}}\Delta x_{1}+\frac{\partial u_{1}}{\partial x_{2}}\Delta x_{2}\\ u_{2}(x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2})&\approx u_{2}+\frac{\partial u_{2}}{\partial x_{1}}\Delta x_{1}+\frac{\partial u_{2}}{\partial x_{2}}\Delta x_{2}. \end{aligned} \]
Pomocí maticového součinu přehledněji \[ \begin{pmatrix} u_1 (x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2}) \\ u_1 (x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2}) \end{pmatrix} \approx \begin{pmatrix} u_1\\u_2 \end{pmatrix}+ \begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac{\partial u_{1}}{\partial x_{2}}\\ \frac{\partial u_{2}}{\partial x_{1}} & \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} \begin{pmatrix} \Delta x_1 \\ \Delta x_2 \end{pmatrix}. \]
Matice, která se nemění transponováním, tj. \(a_{ij}=a_{ji}\) se nazývá symetrická. Matice, která splňuje \(a_{ij}=-a_{ji}\) se nazývá antisymetrická. Pro libovolnou čtvercovou matici \(A\) platí \[A=\frac{A+A^T}2+\frac{A-A^T}2.\] První matice v tomto součtu je symetrická a druhá antisymetrická. Takto je možné rozložit matici na součet symetrické a antisymetrické matice. Například matice \[A= \begin{pmatrix} -4 & 7 \\ -1 & 2 \end{pmatrix} \] má tento rozklad ve tvaru \[A= \begin{pmatrix} -4 & 3 \\ 3 & 2 \end{pmatrix} + \begin{pmatrix} 0 & 4 \\ -4 & 0 \end{pmatrix}. \] Tento trik použijeme pro odvození tvaru tenzoru malých deformací ze vzorce pro lineární aproximaci vektorové funkce.
Antisymetrická matice souvisí s rotací. Vskutku, pokud od matice malých rotací \[R_{\theta,0}= \begin{pmatrix} 1 & - \theta\\ \theta & 1 \end{pmatrix} \] odečteme jednotkovou matici, dostaneme matici antisymetrickou \[R_{\theta,0}-I= \begin{pmatrix} 0 & - \theta\\ \theta & 0 \end{pmatrix}. \]

Metodami lineární algebry kombinovanými s diferenciálním počtem dokážeme ve zobrazení identifikovat tenzor malých deformací, složku související jenom se změnou tvaru. Odfiltrujeme tak posun či rotaci, které se změnou tvaru nesouvisí. Zdroj: pixabay.com
Zobrazení roviny do sebe, kterým je možné popsat deformaci tělesa působením síly je možné popsat dvojicí funkcí \(u_1(x_1,x_2)\), \(u_2(x_1,x_2)\). Lineární aproximace těchto funkcí v okolí bodu \((x_1,x_2)\) dávají (vpravo pro stručnost vynecháváme argument \((x_1,x_2)\)) v maticovém tvaru \[ \begin{pmatrix} u_1 (x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2}) \\ u_1 (x_{1}+\Delta x_{1}, x_{2}+\Delta x_{2}) \end{pmatrix} \approx \begin{pmatrix} u_1\\u_2 \end{pmatrix}+ \begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac{\partial u_{1}}{\partial x_{2}}\\ \frac{\partial u_{2}}{\partial x_{1}} & \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} \begin{pmatrix} \Delta x_1 \\ \Delta x_2 \end{pmatrix}. \] Člen \(\begin{pmatrix} u_1\\u_2 \end{pmatrix}\) je posunutí, proto nás zajímá až druhý člen, obsahující deformaci. Pokud matici \[D= \begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac{\partial u_{1}}{\partial x_{2}}\\ \frac{\partial u_{2}}{\partial x_{1}} & \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} \] rozdělíme stejným obratem jako na předešlém slidu na součet symetrické a antisymetrické matice, dostaneme \[D= \overbrace{\begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)\\ \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)& \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} }^{D_{\text{sym}}} + \underbrace{ \begin{pmatrix} 0 & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)\\ - \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)& 0 \end{pmatrix}}_{D_{\text{asym}}}.\] Druhá část reprezentuje pootočení, což snadno nahlédneme, pokud tuto informaci sečteme s identitou reprezentovanou jednotkovou maticí na \[ D_{\text{asym}}+I=\begin{pmatrix} 1 & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)\\ - \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}-\frac{\partial u_{2}}{\partial x_{1}}\right)& 1 \end{pmatrix} \] abychom měli celou část zobrazení (ne jenom deformaci). Porovnáním s maticí malých rotací \[R_{\theta,0}= \begin{pmatrix} 1 & - \theta\\ \theta & 1 \end{pmatrix} \] odvozenou na jednom z předchozích slidů získáme přímo pootočení. V teorii deformace nás zajímá spíše symetrická část, tj. matice \[ D_{\text{sym}}=\begin{pmatrix} \frac{\partial u_{1}}{\partial x_{1}} & \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)\\ \frac 12\left(\frac{\partial u_{1}}{\partial x_{2}}+\frac{\partial u_{2}}{\partial x_{1}}\right)& \frac{\partial u_{2}}{\partial x_{2}} \end{pmatrix} \] popisující změnu tvaru a nazývaná tenzor malých deformací. Ten se ještě někdy rozděluje na součet vhodného konstantního násobku jednotkové matice (souvisí se zvětšením nebo zmenšením, tj. se změnou objemu) a deviátor (souvisí se zmenou tvaru bez započtení zvětšení či zmenšení).
Pro využití v dřevařských úlohách viz též A. Požgaj, Štruktúra a vlastnosti dreva str 318 nebo P. Horáček, Fyzikální a mechanické vlastnosti dřeva I, str. 40. Analogicky, ale pro rychlosti, je definován tenzor rychlosti přetvoření (deformační rychlost) používaný v hydrodynamice. Můžeme ji dostat jako derivaci tenzoru malých deformací (při studiu deformací), nebo jako symetrickou část matice vytvořené gradienty jednotlivých komponent rychlosti proudění. Pro proudění vody viz J. Říha, Matematické modelování hydrodynamických a disperzních jevů, kap. 3.3.
Determinant je jedna ze základních číselných chrakteristik čtvercových matic, definice je obecná a založená na permutacích indexů, nebo rekurentní, pomocí Laplaceova rozvoje. My budeme potřebovat jenom dva základni speciální případy.
Poznámka (vlastnosti determinantu).
- Řádky čtvercové matice jsou lineárně nezávislé právě pro matice s nenulovým determinantem.
- Inverzní matice existuje právě pro matice s nenulovým determinantem.
- Soustava lineárních rovnic se čtvercovou maticí má právě jedno řešení právě pro matice s nenulovým determinatem.
- Homogenní soustava lineárních rovnic se čtvercovou maticí má nenulové řešení právě pro matice s nenulovým determinatem.
U zobrazování vektorů pomocí maticového násobení nás velice zajímá, které směry se zachovávají, tj. kdy bude obrazem vektoru jeho násobek.
Definice (vlastní vektor a vlastní hodnota matice).
Řekneme, že nenulový vektor \(\vec u\) je vlastním vektorem matice \(A\) příslušným vlastní hodnotě \(\lambda\), jestliže platí \[A \vec u=\lambda \vec u.\]
Vlastní čísla se nazývají též vlastní hodnoty matice. Každý nenulový vlastní násobek vlastního vektoru je vlastní vektor příslušný téže vlastní hodnotě.

Dřevo není izotropní materiál a nemá stejné vlastnosti v každém směru. Existují ale tři výrazné směry, vzhledem k nimž se dají mechanické a fyzikální vlastnosti popsat snadněji, než vhledem ke směrům ostatním. Matematicky se jedná o vlastní vektory příslušných maticových fyzikálních veličin. Zdroj: http://woodpoint.sk
Příklad. Matice rotace nemá žádnou vlastní hodnotu (pokud tedy uvažujeme vlastní hodnoty v množině reálných čísel), protože pootočením se změní směr všech vektorů. Vlastní hodnoty existují pouze pro otočení o násobky \(180^\circ\).
Příklad. Matice \(\begin{pmatrix} 3 & 0\\ 0 & 3 \end{pmatrix}\) (trojnásobek jednotkové matice) zobrazuje každý vektor na trojnásobek a všechny vektory jsou vlastními vektory této matice. Příslušná vlastní hodnota je \(3\).
Příklad. Matice \(\begin{pmatrix} 3 & 0\\ 0 & 0 \end{pmatrix}\) má vlastní vektor \((1,0)\) příslušný vlastní hodnotě \(3\) a vlastní vektor \((0,1)\) příslušný vlastní hodnotě \(0\). Protože vlastními vektory jsou i nenulové násobky, je vlastním vektorem každý nenulový vektor, který má nulovou druhou komponentu (vlastní hodnota je \(3\)) nebo první komponentu (vlastní hodnota je \(0\)).
Příklad. Platí \(\begin{pmatrix} 3 & -2\\ -1 & 4 \end{pmatrix} \begin{pmatrix} 2\\1 \end{pmatrix} = \begin{pmatrix} 4\\2 \end{pmatrix}\) a matice \(\begin{pmatrix} 3 & -2\\ -1 & 4 \end{pmatrix}\) má vlastní vektor \((2,1)\) příslušný vlastní hodnotě \(2\). Vlatním vektorem je i každý nenulovvý násobek vektoru \((2,1)\).
Vlastní vektory jsou nesmírně důležité, protože definují směry, podél nichž se zobrazení chová "pěkně". Tímto zobrazením může být třeba to, jak se působení vnější síly na těleso projeví na deformaci tohoto tělesa nebo jak se gradient teploty nebo vlhkosti projeví na proudění tepla či vody ve dřevě, půdě nebo jiném materiálu. Často se v aplikacích maticové zobrazení objevuje v konstitučních vztazích, vztazích mezi podnětem a materiálovou odezvou. Vlastní směry jsou tedy směry, ve kterých má odezva stejný směr jako podnět.
Pro pravidelně rostlé dřevo je snadné tyto směry určit, jsou to anatomické směry dřeva. Pro zkroucené dřevo nebo při studiu proudění vody, vzduchu či ropy v půdě to již tak snadné není a je nutné tyto směry vypočítat. To se naučíme později.
V aplikacích často bývá matice symetrická a u takové matice vlastní vektory vždy existují.
Pojmy lineární algebry spolu krásně souvisí. Definice těchto pojmů si můžete zopakovat v materiálech k základnímu kurzu matematiky z prvního ročníku.
Věta.
Buď \(A\) čtvercová matice řádu \(n\). Následující výroky jsou ekvivalentní:
- Řádky matice \(A\) jsou tvořeny lineárně nezávislými vektory.
- Sloupce matice \(A\) jsou tvořeny lineárně nezávislými vektory.
- K matici \(A\) existuje matice inverzní \(A^{-1}\).
- Matice \(A\) je regulární, tj. \(\det A\neq 0\).
- Soustava lineárních rovnic \[AX=B\] má pro libovolnou pravou stranu \(B\) jediné řešení.
- Homogenní soustava lineárních rovnic \[AX=0\] má pouze nulové řešení.
- Každý vektor z \(\mathbb R^n\) lze vyjádřit jako lineární kombinaci vektorů tvořených řádky (sloupci) matice \(A\), a to jednoznačně, až na pořadí.
Například je-li \(\vec q\) vlastním vektorem matice \(A\) příslušným vlastní hodnotě \(\lambda\), platí \[A\vec q=\lambda \vec q.\] Odsud \[\begin{aligned}A\vec q-\lambda \vec q&=0\\ A\vec q-(\lambda I )\vec q &=0\\ (A-\lambda I )\vec q &=0\end{aligned}\] kde \(I\) je jednotková matice. Pokud chápeme poslední rovnost jako soustavu rovnic s koeficienty \((A-\lambda I)\), nulovou pravou stranou a nenulovým řešením \(\vec q\) (tj. bod 6 předchozí věty neplatí), musí být determinant matice \(A-\lambda I\) nulový (tj. bod 4 předchozí věty neplatí). Tím je motivována následující definice a dokázána následující věta.
Definice (charakteristická rovnice, charakteristický polynom).
Rovnice \[\det (A-\lambda I)=0\] s neznámou \(\lambda\) se nazývá charakteristická rovnice matice \(A\). Výraz na levé straně této rovnice je polynom proměnné \(\lambda\) a nazývá se charakteristický polynom matice \(A\).
Důsledek (vlastní čísla).
Vlastní čísla matice \(A\) jsou právě řešení charakteristické rovnice.